麦克斯韦-玻尔兹曼分布（综述）

                     

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章。

　　 在物理学中（特别是在统计力学中），麦克斯韦–玻尔兹曼分布（Maxwell–Boltzmann distribution，或称麦克斯韦分布）是一种特定的概率分布，以詹姆斯·克拉克·麦克斯韦和路德维希·玻尔兹曼的名字命名。

　　 该分布最初被定义并用于描述理想气体中粒子的速度分布，在这种理想化模型中，粒子在静止容器内自由运动，彼此之间没有相互作用，除了极短暂的碰撞，在这些碰撞中粒子与其他粒子或热环境交换能量和动量。在此语境下，“粒子” 仅指气体粒子（即原子或分子），并假设该粒子系统已达到热力学平衡状态。\(^\text{[1]}\) 这类粒子的能量遵循麦克斯韦–玻尔兹曼统计，其速度的统计分布可通过将粒子能量与动能等同来推导得出。

　　 从数学上讲，麦克斯韦–玻尔兹曼分布是具有三个自由度的卡方分布（对应于欧几里得空间中速度矢量的三个分量），其尺度参数以与 $T/m$（温度与粒子质量之比）的平方根成正比的单位来度量速度。\(^\text{[2]}\)

　　 麦克斯韦–玻尔兹曼分布是气体动理论的结果，气体动理论为许多基本的气体性质（包括压强和扩散）提供了简化的解释。\(^\text{[3]}\) 麦克斯韦–玻尔兹曼分布本质上适用于三维空间中粒子的速度分布，但结果仅依赖于速率（即速度的大小），而与方向无关。粒子速率的概率分布表示哪些速率更为常见：一个随机选取的粒子，其速率将以该分布为依据进行抽样，因此落在某一速率范围内的可能性会高于另一速率范围。气体动理论适用于经典理想气体，这是一种对真实气体的理想化模型。对于真实气体，存在多种效应（如范德华力、涡流流动、相对论速度极限以及量子交换相互作用），可能使其速率分布偏离麦克斯韦–玻尔兹曼形式。然而，在常温下的稀薄气体表现得非常接近理想气体，其速率分布可被麦克斯韦分布很好地近似描述。这一点对于理想等离子体也成立，即在足够低密度下的电离气体。\(^\text{[4]}\)

　　 该分布最早由麦克斯韦于 1860 年以启发式方法推导得到。\(^\text{[5][6]}\) 随后在 19 世纪 70 年代，玻尔兹曼对该分布的物理起源进行了深入研究。该分布还可以通过最大化系统熵的原理推导出来。以下是一些推导方法的列表：

  1. 在相空间中，通过最大熵原理得到的最大熵概率分布，其约束条件是系统的平均能量守恒：$\langle H \rangle = E$
  2. 正则系综方法。

1. 分布函数

　　 对于一个包含大量相同、非相互作用、非相对论性经典粒子且处于热力学平衡状态的系统，在三维速度空间中以速度矢量 $\mathbf{v}$ 为中心、体积为 $d^3\mathbf{v}$ 的无限小区域内的粒子所占比例由下式给出： $$ f(\mathbf{v})\, d^3\mathbf{v} = \left( \frac{m}{2\pi k_{\text{B}} T} \right)^{3/2} \exp\left( -\frac{m v^2}{2 k_{\text{B}} T} \right)\, d^3\mathbf{v},~ $$ 其中：

图
图 1：下图显示了在温度为 298.15 K（25 °C）时几种稀有气体的速率概率密度函数。纵轴的单位是 s/m，因此曲线下任意区间的面积（即粒子速率落在该区间的概率）是无量纲的。

　　 我们可以将速度空间中的体积元写为：$d^3\mathbf{v} = dv_x\, dv_y\, dv_z$，这是在标准笛卡尔坐标系中的表示；也可以写为：$d^3\mathbf{v} = v^2\, dv\, d\Omega$,这是在标准球坐标系中的表示，其中：$d\Omega = \sin{v_{\theta}}\, dv_{\phi}\, dv_{\theta}$ 是立体角元，且：$v^2 = |\mathbf{v}|^2 = v_x^2 + v_y^2 + v_z^2$。

　　 当粒子仅沿一个方向（例如 $x$ 方向）运动时，其麦克斯韦分布函数为： $$ f(v_x)dv_x = \sqrt{ \frac{m}{2\pi k_{\text{B}} T} }\exp\left( -\frac{m v_x^2}{2 k_{\text{B}} T} \right)dv_x~ $$ 这个公式可以通过对前述三维速度分布函数在 $v_y$ 和 $v_z$ 上积分而得到。

　　 注意到函数 $f(v)$ 的对称性，可以对立体角进行积分，从而将速率的概率分布函数写为如下形式：\(^\text{[7]}\) $$ f(v) = \left( \frac{m}{2\pi k_{\text{B}} T} \right)^{3/2} 4\pi v^2 \exp\left( -\frac{m v^2}{2 k_{\text{B}} T} \right).~ $$ 这个概率密度函数表示的是单位速率下，在速率接近 $v$ 附近发现一个粒子的概率。这个公式就是麦克斯韦–玻尔兹曼分布（如信息框中所示），其分布参数为：$a = \sqrt{k_{\text{B}} T/m}$ 麦克斯韦–玻尔兹曼分布等价于具有三个自由度、尺度参数为 $a = \sqrt{k_{\text{B}} T / m}$ 的卡方分布（chi 分布）。

　　 该分布所满足的最简单的常微分方程为： $$ 0 = k_{\text{B}} T\, v\, f'(v) + f(v)\left(m v^2 - 2 k_{\text{B}} T\right), \quad f(1) = \sqrt{\frac{2}{\pi}} \left( \frac{m}{k_{\text{B}} T} \right)^{3/2} \exp\left( -\frac{m}{2 k_{\text{B}} T} \right)~ $$ 或者用无量纲形式表示为： $$ 0 = a^2 x f'(x) + \left(x^2 - 2 a^2\right) f(x), \quad f(1) = \frac{1}{a^3} \sqrt{\frac{2}{\pi}} \exp\left(-\frac{1}{2 a^2} \right).~ $$ 通过 Darwin–Fowler 平均值方法，可以精确地导出麦克斯韦–玻尔兹曼分布。

2. 向二维麦克斯韦–玻尔兹曼分布的弛豫过程

图
图 2：二维气体弛豫至麦克斯韦–玻尔兹曼速率分布的模拟

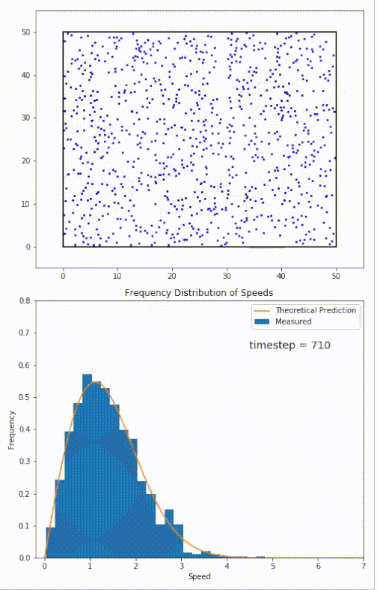
　　 对于被限制在平面内运动的粒子，其速率分布由下式给出： $$ P(s < |\mathbf{v}| < s + ds) = \frac{m s}{k_{\text{B}} T} \exp\left( -\frac{m s^2}{2 k_{\text{B}} T} \right) ds~ $$ 这个分布用于描述处于平衡态的系统。然而，大多数系统一开始并不在平衡状态。系统向平衡态的演化过程由玻尔兹曼方程所控制。该方程预测，在短程相互作用下，系统最终的平衡速度分布将遵循麦克斯韦–玻尔兹曼分布。右图展示了一个分子动力学（MD）模拟：900 个硬球粒子被限制在一个矩形区域内运动，粒子之间通过完全弹性碰撞相互作用。该系统初始处于非平衡态，但其速度分布（蓝色）很快就收敛到二维麦克斯韦–玻尔兹曼分布（橙色）。

3. 典型速率

图
图 3

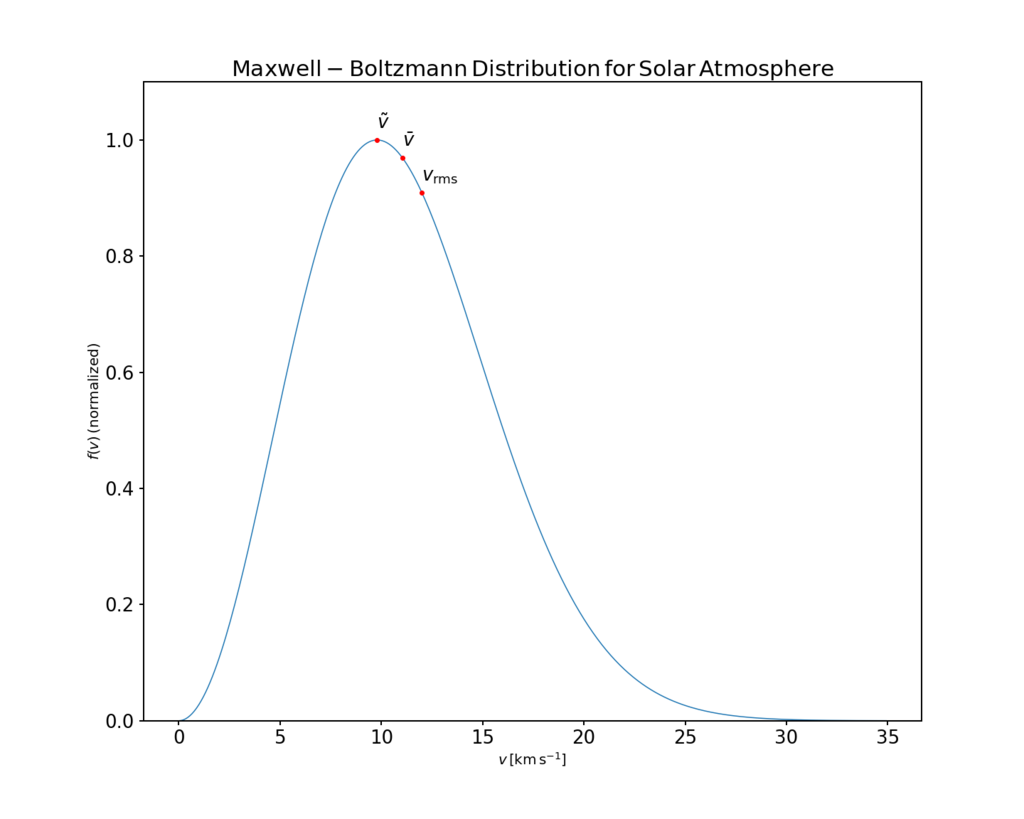
　　 平均速率 $\langle v \rangle$、最可能速率（众数）$v_p$ 和均方根速率 $\sqrt{ \langle v^2 \rangle }$ 都可以通过麦克斯韦分布的性质推导得到。

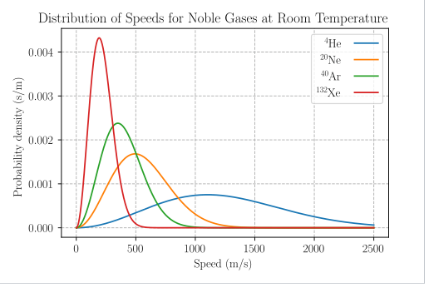
　　 这在近似理想的单原子气体（如氦气）中效果很好，同时也适用于像双原子氧气这样的分子气体。这是因为，尽管分子气体由于具有更多自由度而具有更大的热容（即在相同温度下具有更高的内能），但它们的平动动能（从而速率）并不因此改变。\(^\text{[8]}\)

　　 其中：

　　 对于双原子氮气（$\mathrm{N}_2$，空气的主要成分）\(^\text{[注 1]}\) 在室温（300 K）下，其最可能速率为： $$ v_p \approx \sqrt{ \frac{2 \cdot 8.31 \mathrm{J \cdot mol^{-1} \cdot K^{-1}} \cdot 300 \mathrm{K}}{0.028 \mathrm{kg \cdot mol^{-1}}} } \approx 422 \mathrm{m/s}~ $$

　　 气体的均方根速率与其声速 $c$ 之间有直接关系： $$ c = \sqrt{\frac{\gamma}{3}}\, v_{\mathrm{rms}} = \sqrt{\frac{f + 2}{3f}}\, v_{\mathrm{rms}} = \sqrt{\frac{f + 2}{2f}} v_p~ $$ 其中：$\gamma = 1 + \frac{2}{f}$ 是绝热指数；$f$ 是单个气体分子的自由度数目。以上例为准，在 300 K 时，双原子氮气（近似为空气）具有 $f = 5$ 个自由度 \(^\text{[注 2]}\)，因此： $$ c = \sqrt{\frac{7}{15}} v_{\mathrm{rms}} \approx 68\% v_{\mathrm{rms}} \approx 84\% v_p \approx 353 \mathrm{m/s}~ $$ 实际空气的声速可以通过使用空气的平均摩尔质量（29 g/mol）近似计算，得到在 300 K 时为约 347 m/s。若考虑湿度变化的修正，误差大约在 0.1% 到 0.6% 之间。

　　 平均相对速度 $$ v_{\text{rel}} \equiv \langle |\mathbf{v}_1 - \mathbf{v}_2| \rangle = \int d^3\mathbf{v}_1\, d^3\mathbf{v}_2\, |\mathbf{v}_1 - \mathbf{v}_2|\, f(\mathbf{v}_1) f(\mathbf{v}_2) = \frac{4}{\sqrt{\pi}} \sqrt{\frac{k_{\text{B}} T}{m}} = \sqrt{2}\, \langle v \rangle~ $$ 其中，三维速度分布为： $$ f(\mathbf{v}) \equiv \left( \frac{2\pi k_{\text{B}} T}{m} \right)^{-3/2} \exp\left( -\frac{1}{2} \frac{m \mathbf{v}^2}{k_{\text{B}} T} \right)~ $$ 该积分可以通过变量代换简化为：$\mathbf{u} = \mathbf{v}_1 - \mathbf{v}_2$：相对速度 $\mathbf{U} = \tfrac{1}{2}(\mathbf{v}_1 + \mathbf{v}_2)$：平均速度,借助这些坐标变换，积分计算将更加简便。

4. 局限性

　　 麦克斯韦–玻尔兹曼分布假设单个粒子的速度远小于光速，即：$T \ll \frac{mc^2}{k_{\text{B}}}$ 对于电子来说，其温度必须满足：$T_e \ll 5.93 \times 10^9\, \mathrm{K}$ 才能满足这一前提条件。

5. 推导与相关分布

麦克斯韦–玻尔兹曼统计

　　 最初的推导由詹姆斯·克拉克·麦克斯韦于 1860 年提出，基于气体动理论中的分子碰撞机制以及速率分布函数的某些对称性。麦克斯韦还早期提出，分子之间的碰撞会促使系统趋向平衡态。\(^\text{[5][6][9]}\) 在麦克斯韦之后，路德维希·玻尔兹曼于 1872 年也从力学角度推导了该分布，并进一步论证由于分子之间的碰撞，气体系统会随时间趋向于这种分布（见 H 定理）。随后在 1877 年，\(^\text{[11]}\) 他又在统计热力学框架下重新推导了这一分布。本节中的推导思路基本遵循玻尔兹曼 1877 年的路径，并从所谓的麦克斯韦–玻尔兹曼统计出发（源自统计热力学）。该统计方法给出了处于某个单粒子微观态的平均粒子数。在某些假设条件下，粒子处于某一微观态的比例的对数与该态能量与系统温度的比值成线性关系：存在常数 $k$ 和 $C$，使得对任意 $i$ 有： $$ -\log\left(\frac{N_i}{N}\right) = \frac{1}{k} \cdot \frac{E_i}{T} + C~ $$ 上述公式的前提假设包括：粒子之间没有相互作用；粒子是经典粒子（即可区分、可独立考虑）；系统处于热平衡状态。\(^\text{[1][12]}\)

　　 通过引入归一化因子，上述关系可以写成如下形式的等式： $$ \frac{N_i}{N} = \frac{\exp\left( -\frac{E_i}{k_{\text{B}} T} \right)}{\sum\limits_j \exp\left( -\frac{E_j}{k_{\text{B}} T} \right)} \tag{1}~ $$ 其中：

　　 式 (1) 分母中的求和项是一个归一化因子，使得所有 $N_i : N$ 的比例之和为 1 —— 换句话说，它是一个配分函数（不过是针对单粒子系统的，而不是通常意义上的整个系统的配分函数）。

　　 由于速度和速率与能量有关，因此公式 (1) 可用于推导气体粒子的速度与温度之间的关系。所需的只是确定能量中的微观态密度，这可以通过将动量空间划分为等大小的区域来完成。

动量矢量的分布

　　 此处假设势能为零，因此系统的所有能量都是动能。对于具有质量的非相对论性粒子，其动能与动量之间的关系为： $$ E = \frac{p^2}{2m} \tag{2}~ $$ 其中 $p^2$ 是动量矢量 $\mathbf{p} = [p_x, p_y, p_z]$ 的平方。

　　 因此，我们可以将公式 (1) 重写为： $$ \frac{N_i}{N} = \frac{1}{Z} \exp\left( -\frac{p_{i,x}^2 + p_{i,y}^2 + p_{i,z}^2}{2m k_{\text{B}} T} \right) \tag{3}~ $$ 其中：

　　 这个 $N_i : N$ 的分布比例关系对应于某分子具有给定动量分量的概率密度函数 $f_{\mathbf{p}}$，因此有： $$ f_{\mathbf{p}}(p_x, p_y, p_z) \propto \exp\left( -\frac{p_x^2 + p_y^2 + p_z^2}{2m k_{\text{B}} T} \right) \tag{4}~ $$ 为了使该概率密度函数归一化（即分子具有某个动量的总概率为 1），需要计算归一化常数。对公式 (4) 中的指数函数在所有 $p_x$、$p_y$、$p_z$ 上进行积分，得到一个因子： $$ \iiint_{-\infty}^{+\infty} \exp\left( -\frac{p_x^2 + p_y^2 + p_z^2}{2m k_{\text{B}} T} \right) dp_x\, dp_y\, dp_z = \left[ \sqrt{\pi} \sqrt{2m k_{\text{B}} T} \right]^3~ $$ 这个积分结果用来确定归一化因子，使概率密度函数 $f_{\mathbf{p}}$ 满足整体积分为 1 的条件。

　　 因此，归一化后的动量分布函数为： $$ f_{\mathbf{p}}(p_x, p_y, p_z) = \left( \frac{1}{2\pi m k_{\text{B}} T} \right)^{3/2} \exp\left( -\frac{p_x^2 + p_y^2 + p_z^2}{2m k_{\text{B}} T} \right) \tag{6}~ $$ 可以看出，该分布是三个相互独立的正态分布变量 $p_x$、$p_y$、$p_z$ 的乘积，每个变量的方差为：$m k_{\text{B}} T$ 此外，可以看出动量的模长服从麦克斯韦–玻尔兹曼分布，其中分布参数为：$a = \sqrt{m k_{\text{B}} T}$ 这一形式的麦克斯韦–玻尔兹曼分布（适用于动量或速度）也可以从气体动理论中，在平衡态下利用 H 定理更基本地推导出来。

能量的分布

　　 能量分布可以通过以下关系确定： $$ f_E(E)dE = f_{\mathbf{p}}(\mathbf{p})d^3\mathbf{p} \tag{7}~ $$ 其中，$d^3\mathbf{p}$ 表示与能量区间 $dE$ 对应的动量相空间体积元素。利用能量与动量之间的球对称色散关系：$E = \frac{|\mathbf{p}|^2}{2m}$ 可以将 $d^3\mathbf{p}$ 表达为： $$ d^3\mathbf{p} = 4\pi |\mathbf{p}|^2\, d|\mathbf{p}| = 4\pi m \sqrt{2mE} dE \tag{8}~ $$ 将公式 (8) 代入 (7)，并将一切用能量 $E$ 表示，得到： $$ \begin{aligned} f_E(E)\,dE &= \left( \frac{1}{2\pi m k_{\text{B}} T} \right)^{3/2} \exp\left( -\frac{E}{k_{\text{B}} T} \right) \cdot 4\pi m \sqrt{2mE}\, dE \\ &= 2 \sqrt{ \frac{E}{\pi} } \left( \frac{1}{k_{\text{B}} T} \right)^{3/2} \exp\left( -\frac{E}{k_{\text{B}} T} \right) dE \end{aligned}~ $$ 最终得出归一化的能量概率密度函数： $$ f_E(E) = 2 \sqrt{ \frac{E}{\pi} } \left( \frac{1}{k_{\text{B}} T} \right)^{3/2} \exp\left( -\frac{E}{k_{\text{B}} T} \right) \tag{9}~ $$ 由于能量与三个独立正态分布动量分量的平方和成正比，因此该能量分布实际上等价于一个伽马分布（Gamma 分布），其：形状参数为：$k_{\text{shape}} = 3/2$ 尺度参数为：$\theta_{\text{scale}} = k_{\text{B}} T$

　　 根据能量均分定理，在平衡态下，能量在三个自由度之间平均分配，因此我们也可以将 $f_E(E) dE$ 表达为一组卡方分布的形式，其中每个自由度上的能量 $\varepsilon$ 服从自由度为 1 的卡方分布：\(^\text{[13]}\) $$ f_\varepsilon(\varepsilon)\, d\varepsilon = \sqrt{ \frac{1}{\pi \varepsilon k_{\text{B}} T} }\, \exp\left( -\frac{\varepsilon}{k_{\text{B}} T} \right) d\varepsilon~ $$ 在平衡态下，该分布对任意自由度数目都成立。例如，如果粒子是具有固定偶极矩的刚性质量偶极子，那么它们将具有三个平动自由度和两个额外的转动自由度。每个自由度上的能量将遵循上述自由度为 1 的卡方分布，而总能量将遵循自由度为 5 的卡方分布。这一点对气体比热理论具有重要意义。

速度矢量的分布

　　 注意到速度的概率密度函数 $f_{\mathbf{v}}$ 与动量的概率密度函数 $f_{\mathbf{p}}$ 成正比，关系为： $$ f_{\mathbf{v}}\, d^3\mathbf{v} = f_{\mathbf{p}} \left( \frac{dp}{dv} \right)^3 d^3\mathbf{v}~ $$ 由于 $\mathbf{p} = m \mathbf{v}$，即动量与速度成正比，代入后得到：

　　 $$ f_{\mathbf{v}}(v_x, v_y, v_z) = \left( \frac{m}{2\pi k_{\text{B}} T} \right)^{3/2} \exp\left( -\frac{m (v_x^2 + v_y^2 + v_z^2)}{2 k_{\text{B}} T} \right)~ $$ 这就是麦克斯韦–玻尔兹曼速度分布。

　　 在速度 $\mathbf{v} = [v_x, v_y, v_z]$ 附近的无穷小体积元 $[dv_x, dv_y, dv_z]$ 内，发现一个粒子的概率为： $$ f_{\mathbf{v}}(v_x, v_y, v_z) dv_x dv_y dv_z~ $$ 与动量分布类似，该速度分布是三个相互独立的正态分布变量 $v_x$、$v_y$、$v_z$ 的乘积，它们的方差为：$k_{\text{B}} T/m$ 我们还可以看出，麦克斯韦–玻尔兹曼速度分布（针对向量速度 $[v_x, v_y, v_z]$）可以表示为三个方向上分布的乘积： $$ f_{\mathbf{v}}(v_x, v_y, v_z) = f_v(v_x) f_v(v_y) f_v(v_z)~ $$ 其中，单个方向上的分布为： $$ f_v(v_i) = \sqrt{ \frac{m}{2\pi k_{\text{B}} T} }\, \exp\left( -\frac{m v_i^2}{2 k_{\text{B}} T} \right)~ $$ 速度矢量的每个分量都服从正态分布，其均值为：$\mu_{v_x} = \mu_{v_y} = \mu_{v_z} = 0$ 标准差为：$\sigma_{v_x} = \sigma_{v_y} = \sigma_{v_z} = \sqrt{ k_{\text{B}} T/m }$ 因此，整个速度向量服从一个三维正态分布，这是多元正态分布的一种特例，其均值为：$\mu_{\mathbf{v}} = \mathbf{0}$ 协方差矩阵为：$\Sigma_{\mathbf{v}} = \left( \frac{k_{\text{B}} T}{m} \right) I$ 其中 $I$ 是 $3 \times 3$ 的单位矩阵。

速率的分布

　　 麦克斯韦–玻尔兹曼速率分布可以直接从上述的速度矢量分布推导而来。注意，速率为： $$ v = \sqrt{v_x^2 + v_y^2 + v_z^2}~ $$ 在球坐标系下的体积元为： $$ dv_x\, dv_y\, dv_z = v^2 \sin\theta\, dv\, d\theta\, d\phi = v^2\, dv\, d\Omega~ $$ 其中 $\phi$ 和 $\theta$ 是速度矢量在球坐标系中的角度。将速度的概率密度函数在立体角 $d\Omega$ 上积分，会引入一个额外因子：$4\pi$ 将速率代入速度分布中（即将三个分量的平方和改为 $v^2$），得到的速率分布函数为： $$ f(v) = \sqrt{\frac{2}{\pi}} \left( \frac{m}{k_{\text{B}} T} \right)^{3/2} v^2 \exp\left( -\frac{m v^2}{2 k_{\text{B}} T} \right)~ $$

6. 在 n 维空间中的分布

　　 在 $n$ 维空间中，麦克斯韦–玻尔兹曼分布变为： $$ f(\mathbf{v}) d^n\mathbf{v} = \left( \frac{m}{2\pi k_{\text{B}} T} \right)^{n/2} \exp\left( -\frac{m |\mathbf{v}|^2}{2k_{\text{B}} T} \right) d^n\mathbf{v}~ $$ 速率分布则变为： $$ f(v) dv = A \exp\left( -\frac{m v^2}{2k_{\text{B}} T} \right) v^{n-1} dv~ $$ 其中，$A$ 是一个归一化常数。

　　 下面这个积分结果非常有用： $$ \int_0^\infty v^a \exp\left( -\frac{m v^2}{2k_{\text{B}} T} \right) dv = \left( \frac{2k_{\text{B}} T}{m} \right)^{\frac{a+1}{2}} \int_0^\infty e^{-x} x^{a/2} dx^{1/2}~ $$ $$ = \left( \frac{2k_{\text{B}} T}{m} \right)^{\frac{a+1}{2}} \int_0^\infty e^{-x} x^{a/2} \cdot \frac{x^{-1/2}}{2} dx~ $$ $$ = \left( \frac{2k_{\text{B}} T}{m} \right)^{\frac{a+1}{2}} \cdot \frac{\Gamma\left( \frac{a+1}{2} \right)}{2}~ $$ 这个公式对于计算涉及速率的期望值、归一化因子等非常关键，特别是在处理麦克斯韦–玻尔兹曼速率分布相关的积分时。

　　 其中 $\Gamma(z)$ 是伽马函数。这个积分结果可以用来计算速率分布函数的矩：

　　 平均速率为： $$ \langle v \rangle = \frac{ \int_0^\infty v \cdot v^{n-1} \exp\left( -\frac{m v^2}{2k_{\text{B}}T} \right) dv }{ \int_0^\infty v^{n-1} \exp\left( -\frac{m v^2}{2k_{\text{B}}T} \right) dv } = \sqrt{ \frac{2k_{\text{B}}T}{m} } \cdot \frac{ \Gamma\left( \frac{n+1}{2} \right) }{ \Gamma\left( \frac{n}{2} \right) }~ $$ 因此，平均速率（又写作 $v_{\text{avg}}$）为：$v_{\text{avg}} = \langle v \rangle = \sqrt{ \frac{2k_{\text{B}}T}{m} } \cdot \frac{ \Gamma\left( \frac{n+1}{2} \right) }{ \Gamma\left( \frac{n}{2} \right) }$

　　 平均平方速率为： $$ \begin{aligned} \langle v^2 \rangle &= \frac{ \int_0^\infty v^2 \cdot v^{n-1} \exp\left( -\frac{m v^2}{2k_{\text{B}}T} \right) dv }{ \int_0^\infty v^{n-1} \exp\left( -\frac{m v^2}{2k_{\text{B}}T} \right) dv } \\ &= \left[\frac{2k_{\text{B}}T}{m} \right] \cdot \frac{ \Gamma\left( \frac{n+2}{2} \right) }{ \Gamma\left( \frac{n}{2} \right) } \\ &= \left[\frac{2k_{\text{B}}T}{m} \right] \cdot \frac{n}{2} = \frac{n k_{\text{B}} T}{m} \end{aligned}~ $$ 这进一步给出了均方根速率： $$ v_{\text{rms}} = \sqrt{ \langle v^2 \rangle } = \sqrt{ \frac{n k_{\text{B}} T}{m} }~ $$ 速率分布函数的导数： $$ \frac{df(v)}{dv} = A \exp\left( -\frac{mv^2}{2k_{\text{B}}T} \right) \left[ -\frac{mv}{k_{\text{B}}T} v^{n-1} + (n-1) v^{n-2} \right] = 0~ $$ 这给出了最可能速率（众数）：$v_{\text{p}} = \sqrt{ (n - 1)k_{\text{B}} T/m }$

7. 参见

8. 注释

  1. 氮气是双原子分子这一事实对计算没有影响。 尽管与单原子气体相比，双原子气体由于自由度更多而具有更高的热容（即在相同温度下有更大的内能），但 $\frac{3RT}{M_m}$ 仍然表示其平均平动动能。 氮气作为双原子分子，仅影响其摩尔质量 $M = 28\, \mathrm{g/mol}$。 参见例如：K. Prakashan，《工程物理》（Engineering Physics，2001 年版），第 2.278 页。
  2. 室温下的氮气被视为 “刚性” 双原子气体，它除了拥有三个平动自由度外，还有两个转动自由度，而振动自由度在该温度下不可激发。

9. 参考文献

  1. Mandl, Franz（2008 年）：《统计物理学》（Statistical Physics），曼彻斯特物理系列（第 2 版），奇切斯特：约翰·威利父子公司（John Wiley & Sons），ISBN 978-0471915331。
  2. Young, Hugh D.; Friedman, Roger A.; Ford, Albert Lewis; Sears, Francis Weston; Zemansky, Mark Waldo（2008 年）：《Sears 与 Zemansky 大学物理：含现代物理》（第 12 版），旧金山：皮尔逊·阿迪生-韦斯利，ISBN 978-0-321-50130-1。
  3. 《物理学百科全书》（Encyclopaedia of Physics，第 2 版），R.G. Lerner、G.L. Trigg，VHC 出版社，1991 年，ISBN 3-527-26954-1，ISBN 0-89573-752-3（VHC Inc.）
  4. N.A. Krall 与 A.W. Trivelpiece：《等离子体物理学原理》，旧金山出版社（，1986 年（及其他许多基础等离子体物理教材）
  5. Maxwell, J.C.（1860 A）：《气体动力学理论的说明。第一部分：完全弹性小球的运动与碰撞》，《伦敦、爱丁堡与都柏林哲学杂志与科学期刊》，第四辑，第 19 卷，第 19–32 页。
  6. Maxwell, J.C.（1860 B）：《气体动力学理论的说明。第二部分：不同种类运动粒子之间的扩散过程》，《伦敦、爱丁堡与都柏林哲学杂志与科学期刊》，第四辑，第 20 卷，第 21–37 页。
  7. Müller-Kirsten, H. J. W.（2013 年）：《统计物理基础》（Basics of Statistical Physics，第 2 版），世界科技出版社（World Scientific），ISBN 978-981-4449-53-3。
  8. Serway, Raymond A.; Faughn, Jerry S.; Vuille, Chris（2011 年）：《大学物理（第一卷）》（College Physics, Volume 1，第 9 版），Cengage Learning，第 352 页，ISBN 9780840068484。
  9. Gyenis, Balazs（2017 年）：《麦克斯韦与正态分布：关于概率、独立性与趋于平衡趋势的一段彩色历史》，《现代物理的历史与哲学研究》，第 57 期，第 53–65 页，arXiv:1702.01411，Bibcode:2017SHPMP..57...53G，doi:10.1016/j.shpsb.2017.01.001，S2CID 38272381。
  10. Boltzmann, L.（1872 年）：《关于气体分子之间热平衡的进一步研究》，《维也纳皇家科学院会议记录：数学与自然科学类》，第 66 卷，第 275–370 页。
  11. Boltzmann, L.（1877 年）：《关于力学热理论第二定律与概率计算之间的关系，即热平衡定律》，《维也纳皇家科学院会议记录：数学与自然科学类，第二分册》，第 76 卷，第 373–435 页，重印于《科学论文集》第 2 卷，第 164–223 页，莱比锡：巴特出版社（Barth），1909 年。英文译本可访问：[http://crystal.med.upenn.edu/sharp-lab-pdfs/2015SharpMatschinsky_Boltz1877_Entropy17.pdf（2021-03-05](http://crystal.med.upenn.edu/sharp-lab-pdfs/2015SharpMatschinsky_Boltz1877_Entropy17.pdf（2021-03-05) 存档于 Wayback Machine）
  12. Parker, Sybil P.（1993 年）：《麦格劳-希尔物理学百科全书》（McGraw-Hill Encyclopedia of Physics，第 2 版），麦格劳-希尔出版社，ISBN 978-0-07-051400-3。
  13. Laurendeau, Normand M.（2005 年）：《统计热力学：基础与应用》，剑桥大学出版社，第 434 页，ISBN 0-521-84635-8。

10. 延伸阅读

11. 外部链接


致读者： 小时百科一直以来坚持所有内容免费无广告，这导致我们处于严重的亏损状态。 长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。 因此，我们请求广大读者热心打赏 ，使网站得以健康发展。 如果看到这条信息的每位读者能慷慨打赏 20 元，我们一周就能脱离亏损， 并在接下来的一年里向所有读者继续免费提供优质内容。 但遗憾的是只有不到 1% 的读者愿意捐款， 他们的付出帮助了 99% 的读者免费获取知识， 我们在此表示感谢。

                     

友情链接： 超理论坛　|　©小时科技 保留一切权利