柯西-施瓦茨不等式（综述）

                     

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科 相关文章。

　　 柯西–施瓦茨不等式（也称为柯西–布尼亚科夫斯基–施瓦茨不等式）是对内积空间中两个向量的内积绝对值的一个上界，其上界由这两个向量范数的乘积给出。它被认为是数学中最重要且应用最广泛的不等式之一。

　　 向量的内积可以用于描述有限和（通过有限维向量空间）、无穷级数（通过序列空间中的向量）以及积分（通过希尔伯特空间中的向量）。柯西于 1821 年首次发表了关于求和形式的不等式。相应的积分形式的不等式由布尼亚科夫斯基于 1859 年发表，赫尔曼·施瓦茨于 1888 年发表了积分形式的现代证明。

1. 不等式的表述

　　 柯西–施瓦茨不等式指出，对于内积空间中的任意两个向量 $\mathbf{u}$ 和 $\mathbf{v}$，都有： $$ |\langle \mathbf{u}, \mathbf{v} \rangle|^2 \leq \langle \mathbf{u}, \mathbf{u} \rangle \cdot \langle \mathbf{v}, \mathbf{v} \rangle~ $$ 其中，$\langle \cdot , \cdot \rangle$ 表示内积运算。例如，实数或复数的点积就是常见的内积形式。每一个内积都对应一个欧几里得 $\ell_2$ 范数，也叫做 “标准范数” 或 “诱导范数”，记作 $|\mathbf{u}|$，其定义为： $$ |\mathbf{u}\| := \sqrt{\langle \mathbf{u}, \mathbf{u} \rangle},~ $$ 其中 $\langle \mathbf{u}, \mathbf{u} \rangle$ 总是一个非负实数（即使内积是复值的）。对上述不等式两边取平方根，就可以得到柯西–施瓦茨不等式更常见的形式，用范数表示为： $$ |\langle \mathbf{u}, \mathbf{v} \rangle| \leq |\mathbf{u}| \cdot |\mathbf{v}|~ $$ 当且仅当 $\mathbf{u}$ 和 $\mathbf{v}$ 线性相关时，上述不等式取等号。\(^\text{[8][9][10]}\)

2. 特殊情形

Sedrakyan 引理 —— 正实数情形

　　 Sedrakyan 不等式，又称为 Bergström 不等式、Engel 形式、Titu 引理（或 T2 引理），表述如下：对于实数 $u_1, u_2, \dots, u_n$ 和正实数 $v_1, v_2, \dots, v_n$，有： $$ \frac{(u_1 + u_2 + \cdots + u_n)^2}{v_1 + v_2 + \cdots + v_n} \leq \frac{u_1^2}{v_1} + \frac{u_2^2}{v_2} + \cdots + \frac{u_n^2}{v_n},~ $$ 或者用求和符号表示为： $$ \left( \sum_{i=1}^{n} u_i \right)^2 \bigg/ \sum_{i=1}^{n} v_i \leq \sum_{i=1}^{n} \frac{u_i^2}{v_i}.~ $$ 这个不等式是柯西–施瓦茨不等式的直接推论，具体地，可以将其看作是在欧几里得空间 $\mathbb{R}^n$ 中对向量点积应用柯西–施瓦茨不等式得到的。

　　 方法是令： $$ u_i' = \frac{u_i}{\sqrt{v_i}}, \quad v_i' = \sqrt{v_i},~ $$ 将其代入向量内积后即可得出上述不等式。这种形式在处理分式型不等式（尤其是分子为完全平方形式）时尤其有用。

$R^2$ —— 平面

图
图 1：欧几里得平面单位圆中的柯西–施瓦茨不等式

　　 实向量空间 $\mathbb{R}^2$ 表示二维平面。它也是二维欧几里得空间，其中的内积就是点积。若 $\mathbf{u} = (u_1, u_2),\quad \mathbf{v} = (v_1, v_2)$ 则柯西–施瓦茨不等式变为： $$ \langle \mathbf{u}, \mathbf{v} \rangle^2 = (\|\mathbf{u}\| \|\mathbf{v}\| \cos \theta)^2 \leq \|\mathbf{u}\|^2 \|\mathbf{v}\|^2,~ $$ 其中 $\theta$ 是向量 $\mathbf{u}$ 和 $\mathbf{v}$ 之间的夹角。

　　 上述形式也许是最容易理解此不等式的方式，因为余弦的平方最大为 1，当且仅当两个向量方向相同或相反时达到最大值。该不等式也可用向量坐标 $u_1$、$u_2$、$v_1$ 和 $v_2$ 表示为： $$ (u_1 v_1 + u_2 v_2)^2 \leq (u_1^2 + u_2^2)(v_1^2 + v_2^2),~ $$ 其中等号成立的充要条件是向量 $(u_1, u_2)$ 与向量 $(v_1, v_2)$ 共线（同向或反向），或其中一个为零向量。

$R^n$：n 维欧几里得空间

　　 在具有标准内积（即点积）的欧几里得空间 $\mathbb{R}^n$ 中，柯西–施瓦茨不等式变为： $$ \left( \sum_{i=1}^{n} u_i v_i \right)^2 \leq \left( \sum_{i=1}^{n} u_i^2 \right) \left( \sum_{i=1}^{n} v_i^2 \right).~ $$ 在此情形下，柯西–施瓦茨不等式可以仅使用初等代数证明，其关键是注意到右侧与左侧之差为： $$ \frac{1}{2} \sum_{i=1}^{n} \sum_{j=1}^{n} (u_i v_j - u_j v_i)^2 \geq 0,~ $$ 或者通过考虑如下关于 $x$ 的二次多项式： $$ (u_1 x + v_1)^2 + \cdots + (u_n x + v_n)^2 = \left( \sum_i u_i^2 \right) x^2 + 2 \left( \sum_i u_i v_i \right) x + \sum_i v_i^2.~ $$ 由于该多项式恒为非负，因此它至多有一个实根，因而其判别式小于等于零，即： $$ \left( \sum_i u_i v_i \right)^2 - \left( \sum_i u_i^2 \right) \left( \sum_i v_i^2 \right) \leq 0.~ $$ 这就得出了柯西–施瓦茨不等式。

$C^n$：n 维复空间

　　 若 $\mathbf{u}, \mathbf{v} \in \mathbb{C}^n$，其中 $\mathbf{u} = (u_1, \ldots, u_n), \quad \mathbf{v} = (v_1, \ldots, v_n)$（其中 $u_1, \ldots, u_n \in \mathbb{C}$，$v_1, \ldots, v_n \in \mathbb{C}$），并且若向量空间 $\mathbb{C}^n$ 上的内积定义为标准复数内积： $$ \langle \mathbf{u}, \mathbf{v} \rangle := u_1 \overline{v_1} + \cdots + u_n \overline{v_n},~ $$ 其中上划线表示复共轭，那么柯西–施瓦茨不等式可以更明确地写为： $$ \left| \langle \mathbf{u}, \mathbf{v} \rangle \right|^2 = \left| \sum_{k=1}^n u_k \overline{v_k} \right|^2 \leq \langle \mathbf{u}, \mathbf{u} \rangle \cdot \langle \mathbf{v}, \mathbf{v} \rangle = \left( \sum_{k=1}^n u_k \overline{u_k} \right) \left( \sum_{k=1}^n v_k \overline{v_k} \right) = \left( \sum_{j=1}^n |u_j|^2 \right) \left( \sum_{k=1}^n |v_k|^2 \right).~ $$ 即： $$ \left| u_1 \overline{v_1} + \cdots + u_n \overline{v_n} \right|^2 \leq \left( |u_1|^2 + \cdots + |u_n|^2 \right) \left( |v_1|^2 + \cdots + |v_n|^2 \right).~ $$

$L^2$ 空间

　　 对于平方可积复值函数所构成的内积空间，有如下不等式成立： $$ \left| \int_{\mathbb{R}^n} f(x)\, \overline{g(x)}\, dx \right|^2 \leq \left( \int_{\mathbb{R}^n} |f(x)|^2\, dx \right) \left( \int_{\mathbb{R}^n} |g(x)|^2\, dx \right).~ $$ 这个不等式是 Hölder 不等式的一个特例。 翻译如下：

3. 应用

分析学中的应用

　　 在任意内积空间中，**三角不等式**可以由柯西–施瓦茨不等式推导出来，推导如下： $$ \|\mathbf{u} + \mathbf{v} \|^2 = \langle \mathbf{u} + \mathbf{v}, \mathbf{u} + \mathbf{v} \rangle = \|\mathbf{u}\|^2 + \langle \mathbf{u}, \mathbf{v} \rangle + \langle \mathbf{v}, \mathbf{u} \rangle + \|\mathbf{v}\|^2~ $$ 由于 $$ \langle \mathbf{v}, \mathbf{u} \rangle = \overline{\langle \mathbf{u}, \mathbf{v} \rangle}~ $$ 所以： $$ \|\mathbf{u} + \mathbf{v} \|^2 = \|\mathbf{u}\|^2 + 2\operatorname{Re} \langle \mathbf{u}, \mathbf{v} \rangle + \|\mathbf{v}\|^2~ $$ 应用柯西–施瓦茨不等式（CS）得： $$ \leq \|\mathbf{u}\|^2 + 2|\langle \mathbf{u}, \mathbf{v} \rangle| + \|\mathbf{v}\|^2 \leq \|\mathbf{u}\|^2 + 2\|\mathbf{u}\|\|\mathbf{v}\| + \|\mathbf{v}\|^2 = (\|\mathbf{u}\| + \|\mathbf{v}\|)^2~ $$ 对两边取平方根，得到三角不等式： $$ \|\mathbf{u} + \mathbf{v} \| \leq \|\mathbf{u} \| + \|\mathbf{v} \|~ $$ 此外，柯西–施瓦茨不等式还可用于证明：内积是关于其自身诱导的拓扑结构下的连续函数。\(^\text{[11][12]}\)

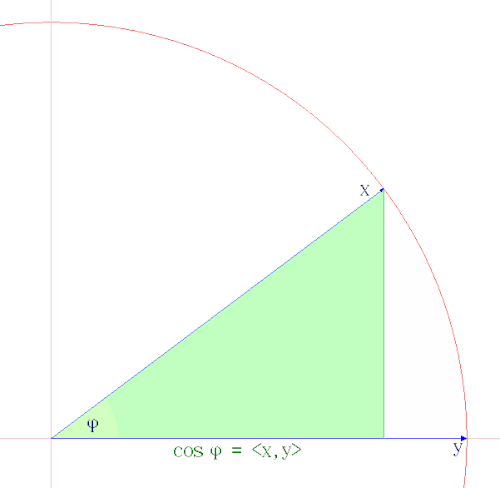
几何学

　　 柯西–施瓦茨不等式使我们能够将 “两向量之间的角度” 这一概念扩展到任意实内积空间中，其定义为：\(^\text{[13][14]}\) $$ \cos \theta_{\mathbf{u}\mathbf{v}} = \frac{\langle \mathbf{u}, \mathbf{v} \rangle}{\|\mathbf{u}\| \|\mathbf{v}\|}.~ $$ 柯西–施瓦茨不等式证明了该定义是合理的，因为右侧表达式的值始终位于区间 $[ -1, 1 ]$ 之间，这就为我们将（实）Hilbert 空间视为欧几里得空间的推广提供了正当性。 在复内积空间中，也可以使用这个不等式来定义角度，不过需要取右侧表达式的绝对值或实部，\(^\text{[15][16]}\)—— 这种方法在从量子保真度中提取度量时尤其常见。

概率论

　　 设 $X$ 和 $Y$ 为随机变量，则协方差不等式为：\(^\text{[17][18]}\) $$ \operatorname{Var}(X) \geq \frac{\operatorname{Cov}(X, Y)^2}{\operatorname{Var}(Y)}.~ $$ 我们可以将随机变量的乘积的期望定义为内积： $$ \langle X, Y \rangle := \operatorname{E}(XY),~ $$ 在这种定义下，柯西–施瓦茨不等式变为： $$ |\operatorname{E}(XY)|^2 \leq \operatorname{E}(X^2)\operatorname{E}(Y^2).~ $$ 为了利用柯西–施瓦茨不等式证明协方差不等式，设：$\mu = \operatorname{E}(X), \quad \nu = \operatorname{E}(Y)$ 则有： $$ \begin{aligned} |\operatorname{Cov}(X, Y)|^2 &= |\operatorname{E}[(X - \mu)(Y - \nu)]|^2 \\ &= |\langle X - \mu, Y - \nu \rangle|^2 \\ &\leq \langle X - \mu, X - \mu \rangle \cdot \langle Y - \nu, Y - \nu \rangle \\ &= \operatorname{E}[(X - \mu)^2] \cdot \operatorname{E}[(Y - \nu)^2] \\ &= \operatorname{Var}(X) \cdot \operatorname{Var}(Y), \end{aligned}~ $$ 其中 $\operatorname{Var}$ 表示方差，$\operatorname{Cov}$ 表示协方差。

4. 证明

　　 除了下述方法外，柯西–施瓦茨不等式还有许多不同的证明方式。\(^\text{[19][5][7]}\) 在查阅其他资料时，读者常会遇到两个混淆点：第一，部分作者将内积符号 $\langle \cdot, \cdot \rangle$ 定义为对第二个变量是线性的（而非第一个变量）；第二，有些证明只在数域为实数 $\mathbb{R}$ 时成立，不适用于复数域 $\mathbb{C}$。\(^\text{[20]}\) 本节将给出以下定理的两种证明方式：

　　 柯西–施瓦茨不等式设$\mathbf{u}$ 和 $\mathbf{v}$ 是任意内积空间中的向量，其标量域为 $\mathbb{F}$，其中 $\mathbb{F}$ 为实数域 $\mathbb{R}$ 或复数域 $\mathbb{C}$。

　　 则有： $$ \left| \langle \mathbf{u}, \mathbf{v} \rangle \right| \leq \|\mathbf{u}\| \, \|\mathbf{v}\|~ $$ （柯西–施瓦茨不等式）

　　 当且仅当 $\mathbf{u}$ 和 $\mathbf{v}$ 线性相关时，上述不等式取等号。

　　 进一步地，如果： $$ \left| \langle \mathbf{u}, \mathbf{v} \rangle \right| = \|\mathbf{u}\| \, \|\mathbf{v}\|~ $$ 且 $\mathbf{v} \neq \mathbf{0}$，则： $$ \mathbf{u} = \frac{ \langle \mathbf{u}, \mathbf{v} \rangle }{ \|\mathbf{v}\|^2 } \, \mathbf{v}.~ $$ 在下面所给出的两个证明中，针对至少有一个向量为零（或者等价地，当 $\|\mathbf{u}\|\|\mathbf{v}\| = 0$ 时）的平凡情形，其证明过程是相同的。为了避免重复，下面只给出一次该情形的证明。这一部分也包含了上文中 “等号成立的判别条件” 中较容易的一部分证明：即证明了如果 $\mathbf{u}$ 和 $\mathbf{v}$ 线性相关，则有 $$ \left| \langle \mathbf{u}, \mathbf{v} \rangle \right| = \|\mathbf{u}\| \, \|\mathbf{v}\|.~ $$

　　 平凡部分的证明：向量为 $\mathbf{0}$ 的情形，以及等号成立判别条件中的一个方向的证明：

　　 按定义，若且唯若其中一个向量是另一个的数倍，则 $\mathbf{u}$ 和 $\mathbf{v}$ 是线性相关的。若 $\mathbf{u} = c\mathbf{v}$，其中 $c$ 是某个标量，则有： $$ |\langle \mathbf{u}, \mathbf{v} \rangle| = |\langle c\mathbf{v}, \mathbf{v} \rangle| = |c\langle \mathbf{v}, \mathbf{v} \rangle| = |c| \|\mathbf{v}\|\|\mathbf{v}\| = \|c\mathbf{v}\|\|\mathbf{v}\| = \|\mathbf{u}\|\|\mathbf{v}\|~ $$ 这就表明在柯西–施瓦茨不等式中等号成立。若 $\mathbf{v} = c\mathbf{u}$（即 $\mathbf{v}$ 是 $\mathbf{u}$ 的倍数），则有： $$ |\langle \mathbf{u}, \mathbf{v} \rangle| = |\langle \mathbf{v}, \mathbf{u} \rangle| = \|\mathbf{v}\|\|\mathbf{u}\|~ $$ 特别地，如果 $\mathbf{u}$ 和 $\mathbf{v}$ 中至少有一个是零向量，则二者必然线性相关（例如若 $\mathbf{u} = \mathbf{0}$，则有 $\mathbf{u} = c\mathbf{v}$，其中 $c = 0$）。因此，上述计算表明，在这种情况下柯西–施瓦茨不等式同样成立。

　　 因此，柯西–施瓦茨不等式只需要对非零向量进行证明，同时仅需证明等号成立条件中的非平凡方向。

通过毕达哥拉斯定理证明

　　 特殊情形 $\mathbf{v} = \mathbf{0}$ 已在前文证明，因此下文假设 $\mathbf{v} \neq \mathbf{0}$。设 $$ \mathbf{z} := \mathbf{u} - \frac{\langle \mathbf{u}, \mathbf{v} \rangle}{\langle \mathbf{v}, \mathbf{v} \rangle} \mathbf{v}.~ $$ 由内积在第一个参数上的线性性可知： $$ \langle \mathbf{z}, \mathbf{v} \rangle = \left\langle \mathbf{u} - \frac{\langle \mathbf{u}, \mathbf{v} \rangle}{\langle \mathbf{v}, \mathbf{v} \rangle} \mathbf{v}, \mathbf{v} \right\rangle = \langle \mathbf{u}, \mathbf{v} \rangle - \frac{\langle \mathbf{u}, \mathbf{v} \rangle}{\langle \mathbf{v}, \mathbf{v} \rangle} \langle \mathbf{v}, \mathbf{v} \rangle = 0.~ $$ 因此，$\mathbf{z}$ 是一个与 $\mathbf{v}$ 正交的向量（实际上，$\mathbf{z}$ 就是 $\mathbf{u}$ 在与 $\mathbf{v}$ 正交的平面上的投影）。因此，我们可以对下式应用毕达哥拉斯定理： $$ \mathbf{u} = \frac{\langle \mathbf{u}, \mathbf{v} \rangle}{\langle \mathbf{v}, \mathbf{v} \rangle} \mathbf{v} + \mathbf{z}.~ $$ 由此得到： $$ \|\mathbf{u}\|^{2} = \left| \frac{\langle \mathbf{u}, \mathbf{v} \rangle}{\langle \mathbf{v}, \mathbf{v} \rangle} \right|^{2} \|\mathbf{v}\|^{2} + \|\mathbf{z}\|^{2} = \frac{|\langle \mathbf{u}, \mathbf{v} \rangle|^{2}}{(\|\mathbf{v}\|^{2})^{2}} \cdot \|\mathbf{v}\|^{2} + \|\mathbf{z}\|^{2} = \frac{|\langle \mathbf{u}, \mathbf{v} \rangle|^{2}}{\|\mathbf{v}\|^{2}} + \|\mathbf{z}\|^{2} \geq \frac{|\langle \mathbf{u}, \mathbf{v} \rangle|^{2}}{\|\mathbf{v}\|^{2}}.~ $$ 将两边乘以 $\|\mathbf{v}\|^{2}$ 并取平方根，即得出柯西–施瓦茨不等式。 此外，若上式中的不等号实际为等号，则 $\|\mathbf{z}\|^{2} = 0$，因此 $\mathbf{z} = \mathbf{0}$；由 $\mathbf{z}$ 的定义可得出 $\mathbf{u}$ 与 $\mathbf{v}$ 线性相关。 反过来的情况已在本节开头证明，因此证明完成。

通过分析二次多项式的证明

　　 考虑任意一对向量 $\mathbf{u}$ 和 $\mathbf{v}$。定义函数 $p : \mathbb{R} \to \mathbb{R}$，其定义为： $$ p(t) = \langle t \alpha \mathbf{u} + \mathbf{v}, t \alpha \mathbf{u} + \mathbf{v} \rangle~ $$ 其中 $\alpha$ 是满足 $|\alpha| = 1$ 且 $\alpha \langle \mathbf{u}, \mathbf{v} \rangle = |\langle \mathbf{u}, \mathbf{v} \rangle|$ 的复数。这样的 $\alpha$ 总是存在，因为当 $\langle \mathbf{u}, \mathbf{v} \rangle = 0$ 时，可以简单地取 $\alpha = 1$。

　　 由于内积是正定的，$p(t)$ 只能取非负实数值。另一方面，利用内积的双线性性质，可以将 $p(t)$ 展开为： $$ \begin{aligned} p(t) &= \langle t \alpha \mathbf{u}, t \alpha \mathbf{u} \rangle + \langle t \alpha \mathbf{u}, \mathbf{v} \rangle + \langle \mathbf{v}, t \alpha \mathbf{u} \rangle + \langle \mathbf{v}, \mathbf{v} \rangle \\ &= t \alpha \cdot t \overline{\alpha} \langle \mathbf{u}, \mathbf{u} \rangle + t \alpha \langle \mathbf{u}, \mathbf{v} \rangle + t \overline{\alpha} \langle \mathbf{v}, \mathbf{u} \rangle + \langle \mathbf{v}, \mathbf{v} \rangle \\ &= \|\mathbf{u}\|^2 t^2 + 2 |\langle \mathbf{u}, \mathbf{v} \rangle| t + \|\mathbf{v}\|^2. \end{aligned}~ $$ 因此，$p(t)$ 是一个二次多项式（除非 $\mathbf{u} = 0$，但这种情形已在前面讨论过）。由于 $p(t)$ 恒不小于零，其判别式必须小于等于零： $$ \Delta = 4 \left( |\langle \mathbf{u}, \mathbf{v} \rangle|^2 - \|\mathbf{u}\|^2 \|\mathbf{v}\|^2 \right) \leq 0.~ $$ 由此推出了柯西–施瓦茨不等式。\(^\text{[21]}\)

　　 关于等号成立的情形，当且仅当 $\Delta = 0$ 时成立，此时：$p(t) = \left( t \|\mathbf{u}\| + \|\mathbf{v}\| \right)^2$ 取 $t_0 = -\|\mathbf{v}\|/\|\mathbf{u}\|$，则有：$p(t_0) = \langle t_0 \alpha \mathbf{u} + \mathbf{v}, t_0 \alpha \mathbf{u} + \mathbf{v} \rangle = 0$ 从而得到：$\mathbf{v} = -t_0 \alpha \mathbf{u}$ 也就是说，$\mathbf{u}$ 和 $\mathbf{v}$ 线性相关。

5. 推广

　　 柯西–施瓦茨不等式存在多种推广形式。赫尔德不等式（Hölder's inequality）将其推广到了 $L^p$ 范数的情形。更一般地，它可以被看作是巴拿赫空间上线性算子范数定义的一个特殊情形（即当空间是希尔伯特空间时）。在算子理论的背景下，还有更广泛的推广，比如针对算子凸函数和算子代数的推广，其中定义域和/或值域被替换为 C\*-代数或 W\*-代数。

　　 内积可用来定义正线性泛函。例如，在希尔伯特空间 $L^2(m)$ 上（其中 $m$ 是有限测度），标准内积可导出正泛函 $\varphi$，定义为：$\varphi(g) = \langle g, 1 \rangle$ 反过来，任意正线性泛函 $\varphi$ 在 $L^2(m)$ 上都可以用来定义内积：$ \langle f, g \rangle_{\varphi} := \varphi(g^* f)$ 其中 $g^*$ 是 $g$ 的逐点复共轭。在这种语言下，柯西–施瓦茨不等式可以写成 \(^\text{[22]}\)： $$ |\varphi(g^* f)|^2 \leq \varphi(f^* f) \, \varphi(g^* g)~ $$ 它可以逐字推广到 C\*-代数上的正泛函：

　　 C*-代数上正泛函的柯西–施瓦茨不等式\(^\text{[23][24]}\)——若 $\varphi$ 是 C\*-代数 $A$ 上的正线性泛函，则对所有 $a, b \in A$，有： $$ \left|\varphi \left(b^{*}a\right)\right|^{2}\leq \varphi \left(b^{*}b\right)\varphi \left(a^{*}a\right).~ $$

　　 下面两个定理是算子代数中的进一步例子：

　　 Kadison–Schwarz 不等式\(^\text{[25][26]}\)（以理查德·卡迪森命名）——若 $\varphi$ 是一个单位正映射，则对于其定义域内的任意正规元 $a$，都有：$\varphi (a^{*}a)\geq \varphi \left(a^{*}\right)\varphi (a)$ 以及 $$ \varphi \left(a^{*}a\right)\geq \varphi (a)\varphi \left(a^{*}\right)~ $$ 这推广了如下事实： $$ \varphi \left(a^{*}a\right)\cdot 1 \geq \varphi (a)^{*}\varphi (a) = |\varphi (a)|^{2}~ $$ 当 $\varphi$ 是线性泛函时成立。当 $a$ 是自伴元素（即 $a = a^{*}$）时，这一结果有时被称为Kadison 不等式。

　　 柯西–施瓦茨不等式（针对 2-正映射的修正施瓦茨不等式）\(^\text{[27]}\) ——对于 C\*-代数间的 2-正映射 $\varphi$，对其定义域中的任意 $a, b$，有： $$ \varphi (a)^{*} \varphi (a) \leq \Vert \varphi (1) \Vert \cdot \varphi \left(a^{*}a\right)~ $$ 以及 $$ \Vert \varphi \left(a^{*}b\right)\Vert ^{2} \leq \Vert \varphi \left(a^{*}a\right)\Vert \cdot \Vert \varphi \left(b^{*}b\right)\Vert.~ $$ 另一个推广形式是一种细化形式，通过在柯西–施瓦茨不等式两端之间插值得到：

　　 Callebaut 不等式\(^\text{[28]}\) —— 对于实数 $0 \leq s \leq t \leq 1$，有

　　 $$ \left( \sum_{i=1}^{n} a_i b_i \right)^2 \leq \left( \sum_{i=1}^{n} a_i^{1+s} b_i^{1-s} \right) \left( \sum_{i=1}^{n} a_i^{1-s} b_i^{1+s} \right) \leq \left( \sum_{i=1}^{n} a_i^{1+t} b_i^{1-t} \right) \left( \sum_{i=1}^{n} a_i^{1-t} b_i^{1+t} \right) \leq \left( \sum_{i=1}^{n} a_i^{2} \right) \left( \sum_{i=1}^{n} b_i^{2} \right).~ $$ 这个定理可以由 Hölder 不等式 推导而来 \(^\text{[29]}\)。同时，也存在适用于算子和矩阵张量积的非交换版本 \(^\text{[30]}\)。

　　 柯西–施瓦茨不等式以及 Kantorovich 不等式的若干矩阵形式也被应用于线性回归模型中 \(^\text{[31][32]}\)。

6. 参见

7. 注释

8. 引文

  1. O'Connor, J.J.; Robertson, E.F. “赫尔曼·阿曼杜斯·施瓦茨”。苏格兰圣安德鲁斯大学。
  2. Bityutskov, V. I. (2001) [1994]，《布尼亚科夫斯基不等式》，《数学百科全书》，EMS 出版社。
  3. Ćurgus, Branko. “柯西-布尼亚科夫斯基-施瓦茨不等式”。数学系，西华盛顿大学。
  4. Joyce, David E. “柯西不等式（Cauchy's inequality）”（PDF）。数学与计算机科学系，克拉克大学。PDF 档案存档于 2022-10-09。
  5. Steele, J. Michael (2004)。《柯西–施瓦茨大师课程：数学不等式艺术导论》。美国数学学会，第 1 页。ISBN 978-0521546775。……毫无疑问，这是整个数学中应用最广泛、最重要的不等式之一。
  6. Strang, Gilbert (2005 年 7 月 19 日)。“3.2”《线性代数及其应用》第 4 版。康涅狄格州斯坦福：Cengage Learning，第 154–155 页。ISBN 978-0030105678。
  7. Hunter, John K.; Nachtergaele, Bruno (2001)。《应用分析》。世界科学出版社。ISBN 981-02-4191-7。
  8. Bachmann, George; Narici, Lawrence; Beckenstein, Edward (2012 年 12 月 6 日)。《傅里叶与小波分析》。施普林格科学与商业传媒，第 14 页。ISBN 9781461205050。
  9. Hassani, Sadri (1999)。《数学物理学：其基础的现代导论》施普林格出版社，第 29 页。ISBN 0-387-98579-4。等号成立当且仅当 <c|c> = 0 或 |c> = 0。根据 |c> 的定义，可得 |a> 与 |b> 必须成比例。
  10. Axler, Sheldon (2015)。《线性代数的正确打开方式》第 3 版。施普林格国际出版，第 172 页。ISBN 978-3-319-11079-0。该不等式当且仅当 u 与 v 之一为另一个的数量倍时取等号。
  11. Bachman, George；Narici, Lawrence（2012-09-26）。《泛函分析（Functional Analysis）》。科瑞尔出版社，第 141 页。ISBN 9780486136554。
  12. Swartz, Charles（1994-02-21）。《测度、积分与函数空间》。世界科学出版社，第 236 页。ISBN 9789814502511。
  13. Ricardo, Henry（2009-10-21）。《线性代数现代导论（A Modern 》。CRC 出版社（CRC Press），第 18 页。ISBN 9781439894613。
  14. Banerjee, Sudipto；Roy, Anindya（2014-06-06）。《统计学的线性代数与矩阵分析》。CRC 出版社（CRC Press），第 181 页。ISBN 9781482248241。
  15. Valenza, Robert J.（2012-12-06）。《线性代数：抽象数学导论》。施普林格科学与商业传媒，第 146 页。ISBN 9781461209010。
  16. Constantin, Adrian（2016-05-21）。《傅里叶分析及其应用》。剑桥大学出版社，第 74 页。ISBN 9781107044104。
  17. Mukhopadhyay, Nitis（2000-03-22）。《概率与统计推断》。CRC 出版社（CRC Press），第 150 页。ISBN 9780824703790。
  18. Keener, Robert W.（2010 年 9 月 8 日）。《理论统计学：核心课程主题》。施普林格科学与商业媒体，第 71 页。ISBN 9780387938394。
  19. Wu, Hui-Hua；Wu, Shanhe（2009 年 4 月）。《柯西-施瓦茨不等式的多种证明》（PDF）。*八边形数学杂志*，第 17 卷第 1 期，第 221–229 页。ISBN 978-973-88255-5-0。ISSN 1222-5657。存档于 2022-10-09（PDF）。检索于 2016 年 5 月 18 日。
  20. Aliprantis, Charalambos D.；Border, Kim C.（2007 年 5 月 2 日）。《无限维分析：搭便车者指南》。施普林格科学与商业媒体。ISBN 9783540326960。
  21. Rudin, Walter（1987 年）[1966 年]。《实分析与复分析》（第 3 版）。纽约：麦格劳-希尔。ISBN 0070542341。
  22. Faria, Edson de；Melo, Welington de（2010 年 8 月 12 日）。《量子场论的数学方面》。剑桥大学出版社，第 273 页。ISBN 9781139489805。
  23. Lin, Huaxin（2001 年 1 月 1 日）。《可和 C\*-代数分类导论》。世界科学出版社，第 27 页。ISBN 9789812799883。
  24. Arveson, W.（2012 年 12 月 6 日）。《C\*-代数导论》。施普林格科学与商业媒体，第 28 页。ISBN 9781461263715。
  25. Størmer, Erling（2012 年 12 月 13 日）。《算子代数的正线性映射》。施普林格数学专著。施普林格科学与商业媒体。ISBN 9783642343698。
  26. Kadison, Richard V.（1952 年 1 月 1 日）。《广义施瓦茨不等式与算子代数的代数不变量》（*A Generalized Schwarz Inequality and Algebraic Invariants for Operator Algebras*）。*数学年刊*（Annals of Mathematics），第 56 卷第 3 期，第 494–503 页。doi:10.2307/1969657。JSTOR 1969657。
  27. Paulsen, Vern（2002 年）。《完全有界映射与算子代数》。剑桥高级数学研究丛书，第 78 卷。剑桥大学出版社，第 40 页。ISBN 9780521816694。
  28. Callebaut, D.K.（1965 年）。《柯西-施瓦茨不等式的推广》。*数学分析与应用杂志*（J. Math. Anal. Appl.），第 12 卷第 3 期，第 491–494 页。doi:10.1016/0022-247X(65)90016-8。
  29. Callebaut 不等式。AoPS Wiki 词条。
  30. Moslehian, M.S.; Matharu, J.S.; Aujla, J.S.（2011 年）。《非交换 Callebaut 不等式》。线性代数及其应用，第 436 卷第 9 期，第 3347–3353 页。arXiv:1112.3003。doi:10.1016/j.laa.2011.11.024。S2CID 119592971。
  31. Liu, Shuangzhe；Neudecker, Heinz（1999 年）。《柯西-施瓦茨与 Kantorovich 型矩阵不等式综述》。统计论文，第 40 卷，第 55–73 页。doi:10.1007/BF02927110。S2CID 122719088。
  32. Liu, Shuangzhe；Trenkler, Götz；Kollo, Tõnu；von Rosen, Dietrich；Baksalary, Oskar Maria（2023 年）。《Heinz Neudecker 教授与矩阵微分演算》。统计论文，第 65 卷第 4 期，第 2605–2639 页。doi:10.1007/s00362-023-01499-w。S2CID 263661094。

9. 参考文献

10. 外部链接


致读者： 小时百科一直以来坚持所有内容免费无广告，这导致我们处于严重的亏损状态。 长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。 因此，我们请求广大读者热心打赏 ，使网站得以健康发展。 如果看到这条信息的每位读者能慷慨打赏 20 元，我们一周就能脱离亏损， 并在接下来的一年里向所有读者继续免费提供优质内容。 但遗憾的是只有不到 1% 的读者愿意捐款， 他们的付出帮助了 99% 的读者免费获取知识， 我们在此表示感谢。

                     

友情链接： 超理论坛　|　©小时科技 保留一切权利