迭代加深

贡献者：有机物

预备知识　深度优先搜索（DFS）

　　迭代加深是用于优化 DFS 的，DFS 是沿着一条路径一直往下走，一条路走到黑，直到没有路可走了才回溯。但如果存在一课搜索树，树的深度很大，但答案却在深度很浅的右半部分子树中，DFS 会搜很多无用的结点。

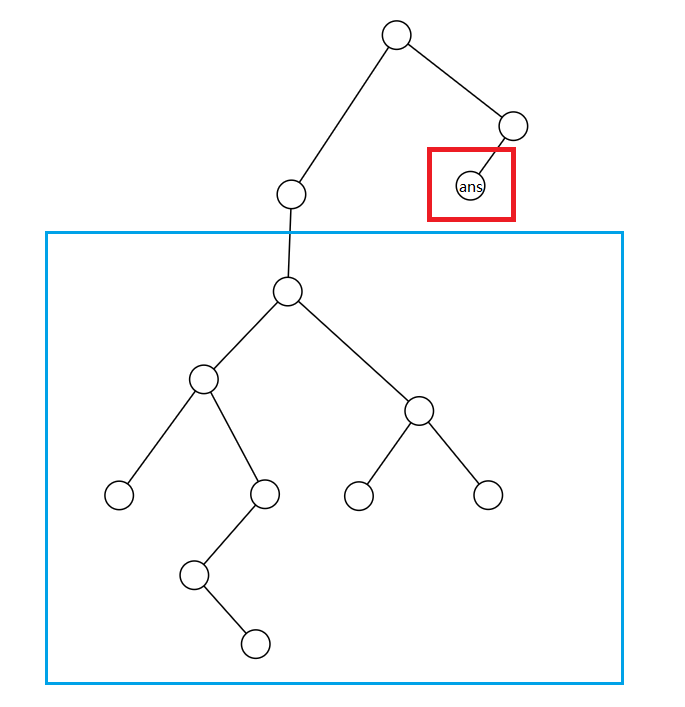
　　如下图，答案在深度很浅的红色部分，普通的 DFS 会先遍历蓝色部分，从而浪费大量的时间。

图 1：搜索树

　　迭代加深的基本思想是：加一个搜索深度的限制，每次只从不超过深度限制的部分进行搜索，如果在限制搜索内无法搜索到答案，那么就将限制扩大一倍。迭代加深看起来很像 BFS，但两者之间还是有区别的，BFS 每次只是扩展当前结点相邻的一层，但迭代加深的本质还是 DFS，还是会沿着一条路径搜索。BFS 的空间复杂度是指数级别的，但 DFS 是和深度呈正比的。假设当前的深度限制为 $k$ ，每次深度限制增加的时候，虽然会重复搜索 $1 \sim k - 1$ 层的结点，但重复的部分比起来总比深度很深、搜索结点呈指数级增长的普通 DFS 要好。

　　 迭代加深的基本框架：

bool dfs(int depth, int max_depth)  
{
    // 如果当前层数 > 深度限制，则直接回溯
    if (depth > max_depth) return false; 
    if () return true;      // 终止条件
    
    /*
    以下为 dfs 内容
    */
    
    return false;   // 找不到答案就回溯
}

int main()
{
    int depth = 0;
    while (!dfs(0, depth)) depth ++ ;   // 迭代加深
    
    return 0;
}

　　 例题：加成序列。

　　数据范围 $n$ 最大为 $100$ ，搜索树的深度最大为 $100$ ，但加成序列的增长规模却很大，所以本题就是搜索深度很深，但答案深度很浅的情况，典型的迭代加深的使用场景，所以就可以使用迭代加深。

　　搜索顺序为：依次枚举序列中的每个位置可以填什么数。

　　剪枝优化：

剪枝一（优化搜索顺序）：可以从大到小枚举每个位置填的数，就可以更快的触发剪枝条件。
剪枝二（排除等效冗余）：因为要找到 $k = x_{i} + x_{j}$ ，假设当前的 $k = 5$ ，序列中存在 $(1, 4)$ 和 $(2, 3)$ 这两种情况，所以可能会重复计算同一个数，所以可以开一个数组用于判断一个数有没有别加过。
剪枝三（最优化剪枝）：如果当前由两个数计算出来的和大于 $n$ 了，直接返回；如果当前计算出来的数小于前一个数，那么也直接返回，因为要保证序列严格单调递增。

　　 C++ 代码：

int n, path[110];

bool dfs(int u, int depth)
{
    if (u > depth) return false;    // 不能超过深度限制
    if (path[u - 1] == n) return true;  // 最后一个数如果等于 n 了

    bool st[N] = {0};
    // 倒着枚举，优化搜索顺序
    for (int i = u - 1; i >= 0; i -- )
        for (int j = i; j >= 0; j -- )
        {
            int s = path[i] + path[j];
            if (s > n || s <= path[u - 1] || st[s]) continue;

            st[s] = true;
            path[u] = s;
            if (dfs(u + 1, depth)) return true;
        }

    return false;
}

int main()
{
    path[0] = 1;    // 第一个数一定是 1
    while (cin >> n, n)
    {
        int depth = 1;
        while (!dfs(1, depth)) depth ++ ;   // 无法找到答案，搜索深度限制就加一
        for (int i = 0; i < depth; i ++ ) cout << path[i] << ' ';
        cout << endl;
    }
    return 0;
}

致读者：小时百科一直以来坚持所有内容免费无广告，这导致我们处于严重的亏损状态。长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。因此，我们请求广大读者热心打赏 ，使网站得以健康发展。如果看到这条信息的每位读者能慷慨打赏 20 元，我们一周就能脱离亏损，并在接下来的一年里向所有读者继续免费提供优质内容。但遗憾的是只有不到 1% 的读者愿意捐款，他们的付出帮助了 99% 的读者免费获取知识，我们在此表示感谢。