复合命题(高中)
贡献者: 欄、停敘; addis
在高中数学中,逻辑是不可忽视的基础工具。尽管教材中逻辑内容的比重有所减少,但掌握逻辑对理解和应用数学知识仍然至关重要。逻辑不仅帮助我们严谨地推导数学定理,还在日常生活中增强了我们分析和解决问题的能力。
当你已经掌握了原子命题的基础后,学习复合命题就成为了你进一步深入逻辑世界的关键一步。顾名思义,复合命题(compound proposition)就是由原子命题通过各种方式(逻辑连接词组合、量词限定变量和条件连接等方式)复合形成的命题。如果用搭积木来比喻的话,我们已知的命题就像一块块积木,而命题连结词就是这些积木的摆放方式,我们可以把不同的积木(命题)摆在一起(连结起来),得到我们想要的状况(命题)。通过学习复合命题,你将学会如何将简单的逻辑拼接成更复杂的推理过程。无论是在解决数学难题时,还是在面对生活中的复杂决策时,理解和应用复合命题都会帮助你更加清晰地思考,增强你的推理能力,为未来的学术挑战和实际应用打下坚实的基础。
顾及到学习此篇文章的同学在高中阶段目前只接触了集合,因此会较多采用初中较为熟悉的 “平面几何” 中的例子,如果你对相关内容有些模糊,可以参见
1. *逻辑连接词
逻辑连接词用于将原子命题组合成更复杂的复合命题,也可以组合使用,表达更复杂的命题。常见的逻辑连接词包括 “且”、“或” 和 “非”。在接下来的部分中,我们将详细介绍这些逻辑连接词的定义、真值表和应用实例。
请注意,尽管这部分内容已经在当前的高中教材中删除,但事实上总在出现,对下面概念的模糊会造成解题时的困惑。
且
在学习数学的过程中,你应该遇见过以下的情况:
- 两个或多个方程需要同时成立,这时会把他们放在一起称为 “方程组”,求解方程组的方法称为 “消元”。
- 证明某个四边形是矩形,就需要满足以下两个条件同时成立:四边形的对角线相等、四个角都是直角。
- 在集合论中,$A \cap B$ 表示集合 $A$ 和 $B$ 的交集,其中的元素必须既属于 $A$,又属于 $B$。
在上面的例子中,一个方程组中方程的关系、用来描述某个事物的多个条件的关系,交集的元素和原始集合的关系,就是 “且”。“消元” 依据的也就是 “且” 这个前提,毕竟只有不论在哪个方程里,同一个变量取的都是同一个值,才能做代换。
真值表是一种用来系统地列出逻辑命题在各种情况下的真值的工具。为了方便刚接触命题概念的同学理解,本文的真值表都给出了两个值,事实上写哪个都可以。通过真值表,我们可以清楚地看到,真值表前面两列是各个命题的真值,最后一列是复合命题在被连接的命题取不同真值时的结果。下面是 “且” 的真值表。
| $A$ | $B$ | $A \land B$ ($A$ 且 $B$) |
| 真(1) | 真(1) | 真(1) |
| 真(1) | 假(0) | 假(0) |
| 假(0) | 真(1) | 假(0) |
| 假(0) | 假(0) | 假(0) |
可以看出,只有当 $A$ 和 $B$ 都是真的时候 $A\land B$($A$ 且 $B$)才是真,否则只要 $A$ 和 $B$ 里面有任何一个是假(当然也包括两个全是假),$A\land B$ 就是假。如果把 “真” 换成 $1$,把 “假” 换成 $0$,则上面的真值表看起来就像是乘法运算,在复杂的逻辑表示时,也经常会像乘法一样,在不引起歧义的情况下,将 $\land$ 省略,记作 $AB$。
或
在学习数学的过程中,你也应该曾遇见过以下几种情况:
- 一元二次方程 $(x-1)(x-2)=0$ 有两个解:$x=1$,$x=2$。这两个解无论代入哪个,原方程都成立。
- 如果一个实数 $x\neq0$,则要么 $x<0$,要么 $x>0$。
- 在集合论中,$A \cup B$ 表示集合 $A$ 和 $B$ 的并集,其中的元素不是在 $A$ 中,就是在 $B$ 中(当然也可以同时在两者之中)。
在上面的例子中,一元二次方程解的关系、不等式之间的关系,并集的元素和原始集合的关系,就是 “或”。
这里需要注意,我们日常生活中使用的 “或者”,例如 “你或者他” 这样的表达,通常意味着二者之一,而不包括两者都选的情况。在逻辑学中,这种情况称为 “异或”3,不过这在高中阶段通常不会详细涉及,此处只是用于扩展视野和解答疑惑。
比如上面的第二个例子中 “要么 $x<0$,要么 $x>0$”,这里的 “或” 其实指的是 $x$ 的实际结果要么在一个区间内,要么在另一个区间内,这种情况在实际中可以理解为 “异或”,因为 $x$ 不可能同时在两个互斥的区间中。但在数学中的 “或” 通常指的是满足任一条件时就可以(即所谓的 “包含或”),且在这个例子中,由于 $x < 0$ 和 $x > 0$ 不能同时成立,或者说即使同时成立的情况不影响最终结果,这里的 “或” 与 “异或” 是等价的,因此我们通常直接将其归为 “或”(认为最终的解集是两个区间的并集)。
在高中数学中,当我们谈到 “或” 时,指的就是只要满足多个条件中的任意一个(而不是只能一个),结果就成立,“或” 的真值表如下:
| $A$ | $B$ | $A \lor B$ ($A$ 或 $B$) |
| 真(1) | 真(1) | 真(1) |
| 真(1) | 假(0) | 真(1) |
| 假(0) | 真(1) | 真(1) |
| 假(0) | 假(0) | 假(0) |
可以看出,只要 $A$ 或 $B$ 有一个是真的时候 $A\lor B$($A$ 或 $B$)就是真,否则也就是两个全是假的时候,$A\land B$ 才是假。由于真值只有 0 和 1,因此若认为 “$1+1=1$” 的话,“或” 看上去就像加法一样。而就像代数中对最简结果的要求是最简多项式一样,一般逻辑表达式的化简结果是由 “或” 连接的。
非
在我们的日常生活中,“否定” 是一种常见的思维方式,它可以帮助我们明确和区分不同的情况。无论是在做决定还是在表达意见时,我们常常会用到 “非” 的概念,例如:
- 当我们说 “今天不是周末” 时,我们实际上是在否定 “今天是周末” 这个命题,明确了今天是工作日。
- 在考试中,如果有人说:“我没有不及格。” 这句话实际上是对 “我不及格” 这个命题的否定,意味着 “我及格了”。
- 朋友问你:“你明天上午有空吗?” 你回答:“我明天上午没有空。” 这里的 “没” 体现在对 “有空” 这个命题的否定,明确表示你有其他安排。
上面的 “不”、“没有”、“没” 都是用来表示命题的否定,就是逻辑上的 “非”。
与之前接触的两个符号不同,“非” 只作用在一个命题上,不论这个命题是原子命题,还是复合命题。“非” 的真值表如下:
| $A$ | $\lnot A$ (非 $A$) |
| 真(1) | 假(0) |
| 假(0) | 真(1) |
“非” 作用在修饰的整个命题上,这件事在原子命题上很容易理解,但是作用在复合命题上时,很容易产生混淆,在 “量词命题” 和 “条件命题” 中需要提起精神注意。
逻辑连接词的性质
就像交集与并集的性质,逻辑连接词也有类似的性质4。注意,表中的 $A,B$ 代表命题,而等号代表着,不论命题真值为何,只要左右条件相同,等号左右的两个命题永远具有相同的真值。表中的 $T,F$ 代表着真值为真、假的命题。下表不要求推导,也不要求记住,此处给出是为了方便查阅,并期望读者能够对照集合中的:空集、全集、交集、并集、补集等概念进行理解。
| 且 $\land$ | 或 $\lor$ | 备注 | |
| 1 | $A\land B = B\land A$ | $A\lor B = B\lor A$ | 交换律(Commutative Law) |
| 2 | $ A \land (B \land C) = (A \land B) \land C$ | $ A \lor (B \lor C) = (A \lor B) \lor C$ | 结合律(Associative Law) |
| 3 | $ A \land (B \lor C) = (A \land B) \lor (A \land C) $ | $ A \lor (B \land C) = (A \lor B) \land (A \lor C) $ | 分配律(Distributive Law) |
| 4 | $ A \lor (A \land B) = A $ | $ A \land (A \lor B) = A $ | 吸收律(Absorption Law) |
| 5 | $A\land A = A$ | $A\lor A = A$ | 幂等律(Idempotent laws) |
| 6 | $ A \land (\lnot A) = F $ | $ A \lor (\lnot A) = T $ | 排中律(Laws of the excluded middle) |
| 7 | $A\land F = F$ | $A\lor F = A$ | 与假命题(F)的关系 |
| 8 | $ A \land T = A $ | $ A \lor T = T $ | 与真命题(T)的关系 |
| 9 | $ \lnot(A \land B) = (\lnot A) \lor (\lnot B) $ | $ \lnot(A \lor B) = (\lnot A) \land (\lnot B) $ | 德摩根定律 |
2. 量词命题
描述关于某些变量的通用性质或存在性质的命题,称为量词命题(quantified propositions)。原本开放命题中真值根据变量取值确定,量词命题使用量词(quantifiers)来限定开放命题中的变量,使得量词命题具有明确的真值。以 “$x$ 是一个偶数” 为例,如果用 “所有” 来限定 $x$,即 “所有的自然数 $x$ 都是偶数”,是假命题,而用 “存在” 来限定 $x$,即 “存在一个自然数 $x$ 是偶数”,则是真命题。
注意,如 “任意 $m>n$” 等单独用量词来限定变量的语句是没有意义的,量词需要在命题中搭配开放命题使用。
全称量词
这里有一些命题:
- 任意直角三角形都满足勾股定理。
- 所有正方形的四边都相等。
- 每一个哺乳动物都是胎生的。
这些命题有真有假,但都有一个共同的特点——需要在陈述中表达所述事物的 “全体” 的含义,这时使用的量词称为全称量词(universal quantifier),记作 $\forall$5,可以读作 “任意”(any)、“所有”(all)、“每一个”(each)等6。
高中数学中涉及的公式、定理、性质一般是全称量词命题,但其适用范围往往会被忽略,在学习时需要注意。
存在量词
这里还有一些命题:
- 存在一个直角三角形,其两直角边相等。
- 有的元素,在自然界中以单质形式存在。
- 13 个人中,至少有一对在同一个月出生。
在陈述中表达所述事物的个体、部分或特例的含义时,使用的量词称为存在量词(existential quantifier,也称作特称量词,particular quantifier),记作 $\exists$7,可以读作 “存在”(exist)、“有”(have)、“至少有一个”(at least)等。
量词命题的否定
在生活中,我们经常听到一些非常 “绝对” 的说法,比如 “所有人都喜欢吃巧克力”,这个 “绝对” 一般就是指 “全称量词”。想要反驳他时,一般会去找一个特例来反驳他,比如:“王某就不喜欢吃巧克力”,就像反证法的精髓就是找到反例,只需要找到一个不喜欢吃巧克力的人,这样就能证明这个说法是错误的,所以否定 “全称量词” 的方法就是存在一个反例。
相反,如果有人说存在某个特别奇怪的事情,比如有人说 “某个地方有会飞的猪”,你可能会觉得这不可能。为了反驳这种说法,一般会尝试列出所有已知的情况,证明 “所有地方都没有会飞的猪”。这就是否定 “存在量词” 的方法:证明在所有情况下,这种情况都不可能发生。
通过将上面两个情况作对比,可以看出,其实 “全称量词 $\forall$” 与 “存在量词 $\exists$” 之间互为否定,即:
看上去需要记两个,但其实对量词命题进行否定时,需要做两件事:
- 将 $\forall$ 换成 $\exists$,$\exists$ 换成 $\forall$;
- 将原本量词限定的开放命题 $P(x)$ 变成它的否定 $\lnot P(x)$。
注意,由于开放命题只要求存在未知量,因此,$P(x)$ 本身也可能是复合命题,在实际操作时,要一层层根据命题的特性来处理命题的否定。
3. 条件命题
在日常生活和学习中,我们经常会遇到 “如果…那么…” 这样的表达方式。比如:
- 如果天气晴朗,那么我们就去郊游
- 若一个数能被 4 整除,则它能被 2 整除
- 三角形内角和 180°,即 “如果一个多边形是三角形,那么它的内角和是 180 度”
这些表达方式实际上都涉及到一个重要的逻辑概念:条件命题。条件命题不仅在生活中十分常见,在计算机领域也被广泛使用。
在高中阶段8,将 “$P\Rightarrow Q$” 理解为表示 “如果命题 $P$ 为真,那么命题 $Q$ 也为真” 就可以了。
总的说来,否定条件命题时,只需要否定后件,而前件则不用动。另外,“$P$ 不能推出 $Q$” 是一种符合语言习惯的表达,但很多同学会因为这个表达而对条件命题的否定造成混淆,不知道应该否定哪个部分。其实在前面的讨论中,我们给出的命题并未涉及其真值的判定。实际上,条件命题既可以是真命题,也可以是假命题。然而,在高中教材中,有时对这些概念的表达不够明确,容易导致初学者在理解条件命题的否定以及充分条件和必要条件时产生困惑。因此,请务必注意本文和教材在表达上的区别。具体说来:
- 在教材中,如果 $P$ 能够推出 $Q$,通常记作 $P\Rightarrow Q$;否则,记作 $P\not\Rightarrow Q$。在这种表达中,$P\Rightarrow Q$ 或 $\Rightarrow$ 符号已经隐含了真值的判断,即认为 “$P$ 能推出 $Q$” 这一命题本身就包含了真假判定。
- 在本文中,我们将命题 “如果 $P$ 能推出 $Q$” 记作 $P\Rightarrow Q$,其否定形式记作 $P\not\Rightarrow Q$。然后,我们再对命题的真值进行讨论:如果 $P\Rightarrow Q$ 是真命题,那么 $P\not\Rightarrow Q$ 为假;反之,如果 $P\Rightarrow Q$ 是假命题,那么 $P\not\Rightarrow Q$ 为真。同时,在不引起歧义的情况下才认为 “$P$ 能推出 $Q$” 这一句话包含真假判定。
*逆命题与否命题
其实,通过条件命题的概念,你可以注意到,条件命题由于其特殊的形式,尽管研究的也是两个命题的关系,但是它和 “且”、“或” 不同,$\Rightarrow$ 符号的左右两个命题并不满足交换律,也就是 $P$(前件)和 $Q$(后件)不能随意互换,这使得二者地位并不 “平等”。下面研究条件命题的前后件改变时的不同的形态。
想象一下,你在和朋友讨论天气。你说:“如果今天下雨,那么我们就不去公园。” 这时路人 A 过来说说:“如果你们不去公园,那么今天就一定下雨了吗?” 路人 B 过来说:“如果今天不下雨,那你们就一定会去公园吗?” 尽管这两个人的语气听起来蛮气人,但这两个问题却是研究中经常会遇到的,与你最开始的表达密切相关的。如果将疑问句改成陈述句,那么就变成了:
- A:如果我们不去公园,那么今天就一定下雨了。
- B:如果今天不下雨,那我们就一定会去公园。
很显然,如果令命题 $P$ 为 “今天下雨”,命题 $Q$ 为 “我们不去公园”,则:
- 你的话:若 $P$,则 $Q$。
- A 的话:若 $Q$,则 $P$。
- B 的话:若 $\lnot P$,则 $\lnot Q$。
显然,这些话之间存在着一些关系,下面针对这些内容给出定义:
注意逆命题和否命题都是针对原命题而言的,描述的是两个条件命题间的关系,这个关系是相对的,会随着原命题的不同而产生变化,比如,如果认为 $P \Rightarrow Q$ 是原命题,则 $Q \Rightarrow P$ 是它的逆命题。反过来,如果认为 $Q \Rightarrow P$ 是原命题,则 $P \Rightarrow Q$ 是它的逆命题,对于否命题也存在这种情况,因此也常说两个命题 “互为逆命题” 或 “互为否命题”。另外,命题的否定和否命题造成很多人的困惑,无法分清。其实,二者只是在中文翻译上,都使用了 “否” 字,造成了理解上的混淆,事实上看二者的英文名称就不易混淆了,下面给出二者的对比:
你应该注意到刚才的例子中,原命题的真值与否命题的真值无关,事实上,原命题的真值与逆命题的真值也无关。这和否定不一样,可以明确知道两个命题的真值关系,给研究带来了一些麻烦。不过,下面这个关系可以保证真值相同。
研究定义 9 可以发现,如果把逆命题 $Q \Rightarrow P$ 当作原命题,则它的否命题是 $\neg Q \Rightarrow \neg P $,而如果把否命题 $\neg P \Rightarrow \neg Q $ 当作原命题,则它的逆命题也是 $\neg Q \Rightarrow \neg P $,二者相同,数学上称为逆否命题。
逆否命题具有一个性质,就是原命题与逆否命题真值相等。而通过之前的论证其实你也能发现,逆命题与否命题也互为逆否命题,因此二者真值也相等。这就为数学研究提供了一个强有力的工具,如果你发现一个命题难以证明,可以先求其逆否命题,再进行证明。当然,前提是能够准确地求得逆否命题,而这往往成为这种证明方式的隐患。因此,熟练地掌握各个概念,在进行操作时能够准确地对命题进行变形和判断,是非常重要的基本功。
充分条件与必要条件
下面我们来研究一下条件命题中,两个命题(前件、后件)的关系。请注意本节使用的 “$P$ 能推出 $Q$” 和 “$P$ 不能推出 $Q$” 的表述均是包含了判定的,即表达命题 $P$ 的 “能力”。
下面的例子有点绕,阅读时请注意前提和视角,不要彼此混淆。
恭喜你读到了这里!希望你依然清晰,不会感到困惑。在分析问题时,我们经常会将以上的思考过程总结为充分条件和必要条件的概念。
需要注意的是:
- 充分/必要条件是两个命题之间的关系,若只说一个命题是充分/必要条件没有意义。
- 讨论充分/必要条件需要在一定的前提下进行。以上两个例子中的前提如:我们讨论的是欧几里得几何中的平面四边形和三角形。
通常在实际解决问题时,需要你先清晰命题 $P$ 和 $Q$ 是什么,然后由于逆命题与原命题的真值关系不确定,还需要分别判定 $P\Rightarrow Q$ 和 $Q\Rightarrow P$ 的真值(即 P、Q 互相能否推出),然后才能得到完整的 $P$ 与 $Q$ 的条件关系。一般题目中如果出现 $P$ 与 $Q$ 的条件关系,指的就是 $P$ 是 $Q$ 的什么条件。完整的关系一共有四种可能10:
| 充分条件 | 不充分条件 | |
| 必要条件 | 充分必要条件 | 必要不充分条件 |
| 不必要条件 | 充分不必要条件 | 既不充分也不必要条件 |
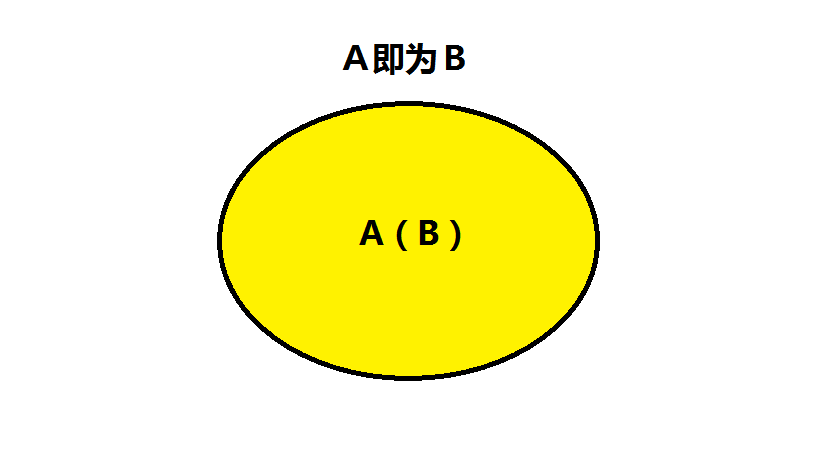
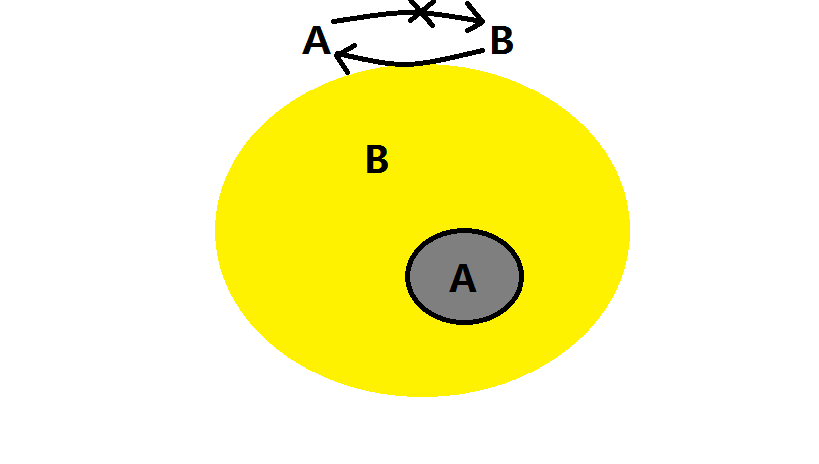
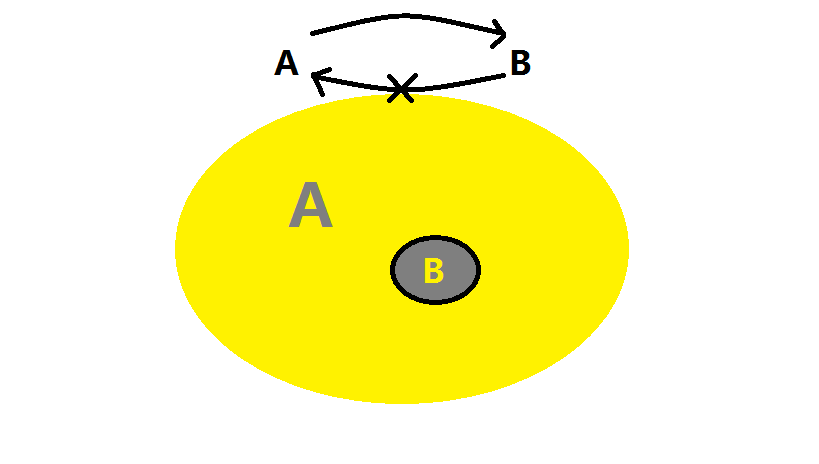
用维恩图来表示命题的 “信息量” 的话,如下图所示:
上面的表格中,必要非充分条件和充分非必要条件都是单向的,非充分非必要条件说明没什么关系,只有充分必要条件是双向的,很特殊,这个时候,$P$ 和 $Q$ 将既是彼此的充分条件,也是彼此的必要条件,这意味着 $P$,$Q$ 命题等价,所提供的信息都一样,两者都没有任何多余的或者缺失的信息。
这里 “当且仅当” 的表达可能会比较陌生,出现的场合就理解为二者能够互相推出或者说二者等价就好。此外,我们还可以将 “充要条件” 作为一个代表,与之前学习过的 “逆否命题” 作为另一个代表进行对比,从而区分条件命题研究中的两个主题。
| 概念 | 定义要点 | 符号表示 | 关键点 |
| 充要条件 | 表达的是两个命题 $P$ 和 $Q$ 的关系 | $P \Leftrightarrow Q$ | $P$ 能推出 $Q$,且 $Q$ 也能推出 $P$。$P$ 和 $Q$ 之间的关系是双向的,缺一不可。 |
| 逆否命题 | 表达的是从一个命题 $P \Rightarrow Q$ 得到的另一个命题 $\neg Q \Rightarrow \neg P$ | $\neg Q \Rightarrow \neg P$ | 逆否命题与原命题具有相同的真值,即原命题为真,则逆否命题也为真,反之亦然。 |
4. 总结
下面这道习题能够帮助你检查自己是否完全掌握了本文的内容。
1. ^ 符号不做硬性要求,下同。
2. ^ 这里提供一个记忆方法,开口向上的像一个将两侧全部装入的容器,开口向下的则像将两侧只各自存在的内容滑出去。这两个符号的开口和与他们关系紧密的 “交集” 和 “并集” 一样。
3. ^ 异或(Exclusive or 或 XOR),通常记作 $A\oplus B$
4. ^ 这些性质被统称为 “布尔代数定律”
5. ^ 这个符号是反写的 A,取 “任意”(any)或 “所有”(all)的首字母 A,且 A 是左右对称,为与一般的 A 做区分,上下反写。
6. ^ 在自然语言中,“每一” 和 “全体” 强调的重点不同,前者强调每一个个体,后者强调整体,但在逻辑中不区分二者。
7. ^ 这个符号是反写的 E,取 “存在”(exist)的首字母 E,且 E 是上下对称,为与一般的 E 做区分,左右反写。
8. ^ 事实上,使用逻辑连接词来定义的 “蕴含” 为:$\lnot P\lor Q$,它与演绎推理的三段论是完全等同的。但涉及这个定义的讨论,已超出高中的范畴,关于蕴含还有很多知识,可以参考命题的连接词。
9. ^ 也就是 $P\Rightarrow Q$ 的否定是 $P\land\neg Q$,这与上一个脚注中的定义也可互相印证。
10. ^ 表中的 “不” 有时也称为 “非”。
友情链接: 超理论坛 | ©小时科技 保留一切权利