高斯散度定理（综述）

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章。

　　 在向量分析中，散度定理，又称高斯定理或奥斯特罗格拉德斯基定理 \(^\text{[1]}\)，是一条将向量场通过闭合曲面的通量与该曲面所包围体积内场的散度联系起来的定理。

　　 更准确地说，散度定理表明：一个向量场在闭合曲面上的曲面积分（即该曲面的 “通量”）等于该曲面所包围区域内散度的体积分。直观地理解，这意味着 “一个区域内所有场源的总和（将汇点视为负源）等于该区域向外的净通量”。

　　 散度定理在物理和工程数学中有着重要地位，尤其是在静电学和流体力学领域。在这些领域中，它通常应用于三维情形。然而，该定理可以推广到任意维度。在一维情形下，它等价于微积分基本定理；在二维情形下，它等价于格林定理。

1. 用液体流动来解释

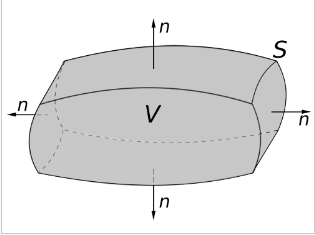
　　 向量场常通过流体速度场（例如气体或液体）来进行说明。运动中的液体在每一点都有一个速度——即速度大小和方向，这个速度可以用一个向量表示，因此液体在某一时刻的速度分布可以看作一个向量场。假设在流体内部放置一个想象的闭合曲面 $S$，它包围了一个体积。该体积内液体的流出通量等于穿过该曲面的体积流率，即速度在该曲面上的曲面积分。

　　 如果流体是不可压缩的，那么闭合体积内的液体总量保持不变；如果体积内没有源或汇，穿过 $S$ 的净通量就是零。即使液体在运动，它可能在曲面 $S$ 的某些位置流入体积，在另一些位置流出体积，但流入和流出的总量始终相等，因此净通量为零。

　　 然而，如果在闭合曲面内存在一个液体源，例如一根向内部注入液体的管道，那么新增的液体会对周围液体施加压力，促使液体向各个方向流出。这会导致通过曲面 $S$ 的净外流，且该外流通量等于通过管道注入的体积流率。同样，如果在曲面 $S$ 内有一个汇或排水口，例如一根排出液体的管道，那么液体在外界压力的作用下会整体向汇点方向流动。穿过曲面 $S$ 的净内流通量等于通过该排水口排出的液体体积流率。

　　 如果曲面 $S$ 内有多个液体的源和汇，通过该曲面的通量可以通过将所有源注入的体积流率相加，再减去所有汇排出的体积流率来计算。液体通过某个源或汇的体积流率（汇的流率取负号）等于该点速度场的散度。因此，将整个体积内的散度积分（即体积分）起来，结果就等于通过曲面 $S$ 的净通量。这就是散度定理 \(^\text{[2]}\)。

　　 散度定理应用于任何形式的守恒定律中，这类定律表明：所有源与汇的总体积（即散度的体积分）等于该体积边界上的净流量 \(^\text{[3]}\)。

2. 数学表述

　　 假设 $V$ 是 $\mathbb{R}^n$ 的一个子集（当 $n = 3$ 时，$V$ 表示三维空间中的一个体积），它是紧致的并且具有分段光滑的边界 $S$（也记作 $\partial V = S$）。如果 $\mathbf{F}$ 是定义在 $V$ 邻域上的连续可微向量场，则有 \(^\text{[4][5]}\)： $$ \iiint_V (\nabla \cdot \vec{F}) \, dV = \iint_S (\vec{F} \cdot \hat{n}) \, dS~ $$ 左边是对体积 $V$ 的体积分，右边是对体积 $V$ 边界的曲面积分。闭集 $\partial V$ 由指向外的法向量来定向，$\mathbf{\hat{n}}$ 是边界 $\partial V$ 上几乎每一点的外指单位法向量。（$\mathrm{d}\mathbf{S}$ 可作为 $\mathbf{n}\,\mathrm{d}S$ 的简写。）从直观描述的角度来看，方程的左边表示体积 $V$ 内所有 “源” 的总量，而右边表示穿过边界 $S$ 的总通量。

3. 非正式推导

　　 散度定理源于这样一个事实：如果将体积 $V$ 分割成若干部分，那么原始体积流出的通量等于每个子体积流出通量的代数和 。这一结论成立的原因在于，新划分出的子体积会产生一些并非原始体积表面的新分界面，而这些分界面上的通量只是从一个子体积流向另一个子体积，在计算所有子体积的流出通量总和时，这部分通量会相互抵消。

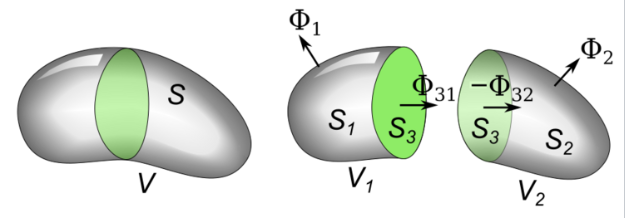
　　 请看示意图：一个封闭、有界的体积 $V$ 被一个表面 $S_3$（绿色部分）分割成两个体积 $V_1$ 和 $V_2$。每个子体积 $V_i$ 的流出通量 $\Phi(V_i)$ 等于穿过其两个表面的通量之和，因此两个子区域的总流出通量为 $$ \Phi(V_1) + \Phi(V_2) = \Phi_1 + \Phi_{31} + \Phi_2 + \Phi_{32}~ $$ 其中，$\Phi_1$ 和 $\Phi_2$ 分别是穿过表面 $S_1$ 和 $S_2$ 的通量；$\Phi_{31}$ 是穿过 $S_3$ 从体积 1 流出的通量，$\Phi_{32}$ 是穿过 $S_3$ 从体积 2 流出的通量。需要注意的是，表面 $S_3$ 同时属于两个体积的边界，而它在两个体积中的外法向方向是相反的。因此，一个体积通过 $S_3$ 流出的通量，恰好等于另一个体积通过 $S_3$ 流出的通量的相反数，两者在求和时相互抵消： $$ \Phi_{31} = \iint_{S_3} \mathbf{F} \cdot \mathbf{\hat{n}}\, dS = -\iint_{S_3} \mathbf{F} \cdot (-\mathbf{\hat{n}})\, dS = -\Phi_{32}~ $$ 因此： $$ \Phi(V_1) + \Phi(V_2) = \Phi_1 + \Phi_2~ $$ 由于表面 $S_1$ 和 $S_2$ 的并集就是整个体积 $V$ 的边界 $S$，于是有： $$ \Phi(V_1) + \Phi(V_2) = \Phi(V)~ $$

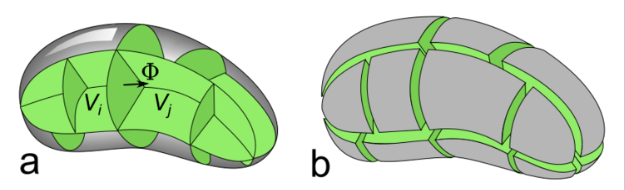
　　 这个原理同样适用于被分成任意多个部分的体积，如图所示。\(^\text{[7]}\) 由于每个内部分割面（绿色部分）在相邻的两个子体积通量中以相反的符号出现，它们会相互抵消，因此通量的贡献只来自外部表面（灰色部分）。而所有子体积的外部表面合起来正好就是原始体积的外表面。 $$ \Phi(V) = \sum_{V_i \subset V} \Phi(V_i)~ $$

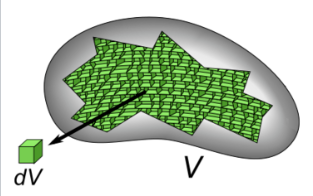
　　 每个体积的通量 $\Phi$ 是向量场 $\mathbf{F}(\mathbf{x})$ 在其表面上的曲面积分： $$ \iint_{S(V)} \mathbf{F} \cdot \mathbf{\hat{n}} \;\mathrm{d} S = \sum_{V_i \subset V} \iint_{S(V_i)} \mathbf{F} \cdot \mathbf{\hat{n}} \;\mathrm{d} S~ $$ 我们的目标是把原始体积划分为无限多个无限小的体积。随着体积分得越来越小，右侧每个子体积的表面积 $S(V_i)$ 趋近于零，因此每个子体积的曲面积分趋向于零。然而，根据散度的定义，通量与体积的比值 $\frac{\Phi(V_i)}{|V_i|}= \frac{1}{|V_i|}\iint_{S(V_i)} \mathbf{F} \cdot \mathbf{\hat{n}} \;\mathrm{d} S$ 括号内的这一部分一般不会消失，而是在体积趋近于零时趋向于散度 $\operatorname{div} \mathbf{F}$。因此： $$ \iint_{S(V)} \mathbf{F} \cdot \mathbf{\hat{n}} \;\mathrm{d} S = \sum_{V_i \subset V} \left( \frac{1}{|V_i|} \iint_{S(V_i)} \mathbf{F} \cdot \mathbf{\hat{n}} \;\mathrm{d} S \right) |V_i|~ $$ 只要向量场 $\mathbf{F}(\mathbf{x})$ 有连续的导数，即使把体积分得无限小，上式依然成立： $$ \iint_{S(V)} \mathbf{F} \cdot \mathbf{\hat{n}} \;\mathrm{d} S = \lim_{|V_i|\to 0} \sum_{V_i \subset V} \left( \frac{1}{|V_i|} \iint_{S(V_i)} \mathbf{F} \cdot \mathbf{\hat{n}} \;\mathrm{d} S \right) |V_i|~ $$ 当 $|V_i|$ 趋近于零时，$|V_i|$ 变为无穷小体积 $\mathrm{d}V$，括号中的部分成为散度，求和变为对整个体积 $V$ 的积分： $$ \iint_{S(V)} \mathbf{F} \cdot \mathbf{\hat{n}} \;\mathrm{d} S = \iiint_{V} \operatorname{div} \mathbf{F} \;\mathrm{d} V~ $$ 由于这一推导完全不依赖于坐标系，这也说明了散度与所用的坐标系无关。

4. 证明

　　 对于欧几里得空间的有界开子集，我们将证明以下结论：\(^\text{[citation needed]}\)

　　 定理—— 设 $\displaystyle \Omega \subset \mathbb{R}^n$ 是一个具有 $C^1$ 边界的开且有界的区域。若 $\displaystyle u \in C^1(O)$，其中 $O$ 是 $\displaystyle \overline{\Omega}$ 的一个开邻域，则对每个 $\displaystyle i \in \{1, \dots, n\}$，有： $$ \int_{\Omega} u_{x_i} \, dV = \int_{\partial \Omega} u \, \nu_i \, dS ,~ $$ 其中 $\displaystyle \nu : \partial \Omega \to \mathbb{R}^n$ 是边界 $\partial \Omega$ 上指向外侧的单位法向量。等价地，可以写为： $$ \int_{\Omega} \nabla u \, dV = \int_{\partial \Omega} u \, \nu \, dS .~ $$ 定理证明\(^\text{[8]}\)

1. 第一步是将问题化简为 $\displaystyle u \in C_c^1(\mathbb{R}^n)$ 的情形。取 $\displaystyle \phi \in C_c^\infty(O)$，使得 $\displaystyle \phi = 1$ 在 $\displaystyle \overline{\Omega}$ 上成立。注意到 $\displaystyle \phi u \in C_c^1(O) \subset C_c^1(\mathbb{R}^n)$，且 $\displaystyle \phi u = u$ 在 $\displaystyle \overline{\Omega}$ 上成立。因此，只需证明该定理对 $\displaystyle \phi u$ 成立即可。由此，我们可以假设 $\displaystyle u \in C_c^1(\mathbb{R}^n)$。
2. 令 $\displaystyle x_{0} \in \partial \Omega$ 为任意一点。 由于假设 $\displaystyle \overline{\Omega}$ 具有 $\displaystyle C^{1}$ 边界，存在 $\displaystyle x_{0}$ 在 $\displaystyle \mathbb{R}^{n}$ 中的一个开邻域 $\displaystyle U$，使得 $\displaystyle \partial\Omega \cap U$ 是某个 $\displaystyle C^{1}$ 函数的图像，并且 $\displaystyle \Omega \cap U$ 位于该图像的一侧。 更具体地说，经过对 $\displaystyle \Omega$ 进行平移和旋转后，可以找到常数 $\displaystyle r > 0$ 和 $\displaystyle h > 0$，以及一个 $\displaystyle C^{1}$ 函数 $g:\mathbb{R}^{n-1} \to \mathbb{R}$， 令 $$ x' = (x_{1}, x_{2}, \dots, x_{n-1}),~ $$ 则有 $$ U = \{x \in \mathbb{R}^n : |x'| < r \ \text{且}\ |x_n - g(x')| < h\}.~ $$ 并且对于任意 $\displaystyle x \in U$： $$ \begin{aligned} x_n = g(x') &\implies x \in \partial \Omega,\\ -h < x_n - g(x') < 0 &\implies x \in \Omega,\\ 0 < x_n - g(x') < h &\implies x \notin \Omega.\\ \end{aligned}~ $$ 由于 $\partial \Omega$ 是紧集，可以用有限多个上述形式的邻域 $U_1, U_2, \dots, U_N$ 覆盖 $\partial \Omega$。注意到 $\{\Omega, U_1, U_2, \dots, U_N\}$ 是 $\overline{\Omega} = \Omega \cup \partial \Omega$ 的一个开覆盖。借助从属于这个覆盖的 $C^{\infty}$ 单位分解，可以把定理的证明归结为两种情况之一：$u$ 在 $\Omega$ 内有紧支撑；$u$ 在某个 $U_j$ 内有紧支撑。如果 $u$ 在 $\Omega$ 内有紧支撑，则对所有 $i \in \{1, 2, \dots, n\}$，有：$\int_{\Omega} u_{x_i} \, dV= \int_{\mathbb{R}^n} u_{x_i} \, dV= \int_{\mathbb{R}^{n-1}} \int_{-\infty}^{\infty} u_{x_i}(x) \, dx_i \, dx' = 0$，这由微积分基本定理直接得出。同时，$\int_{\partial \Omega} u \nu_i \, dS = 0$，因为 $u$ 在 $\partial \Omega$ 的某个邻域上恒为零。因此，若 $u$ 在 $\Omega$ 内有紧支撑，定理成立。于是，我们将问题化简为 $u$ 在某个 $U_j$ 内具有紧支撑的情形。
3. 假设 $u$ 在某个 $U_j$ 内有紧支撑。最后一步是通过直接计算来证明该定理。将符号改为 $U = U_j$ 并引入前面 (2) 式中用于描述 $U$ 的符号。这意味着我们对 $\Omega$ 进行了旋转和平移。由于该定理在坐标旋转和平移下保持不变，这样的化简是合理的。由于 $u(x) = 0$ 在满足 $|x'| \ge r$ 或 $|x_n - g(x')| \ge h$ 的区域内恒成立，对于每个 $i \in \{1, \dots, n\}$，我们有： $$ \begin{aligned} \int_{\Omega} u_{x_i} \, dV &= \int_{|x'| < r} \int_{g(x') - h}^{g(x')} u_{x_i}(x', x_n) \, dx_n \, dx' \\ &= \int_{\mathbb{R}^{n-1}} \int_{-\infty}^{g(x')} u_{x_i}(x', x_n) \, dx_n \, dx'. \end{aligned}~ $$ 当 $i = n$ 时，根据微积分基本定理可得： $$ \int_{\mathbb{R}^{n-1}} \int_{-\infty}^{g(x')} u_{x_n}(x', x_n) \, dx_n \, dx' = \int_{\mathbb{R}^{n-1}} u(x', g(x')) \, dx'.~ $$ 现在固定 $i \in \{1, \dots, n-1\}$ 注意到： $$ \int_{\mathbb{R}^{n-1}} \int_{-\infty}^{g(x')} u_{x_i}(x', x_n) \, dx_n \, dx' = \int_{\mathbb{R}^{n-1}} \int_{-\infty}^{0} u_{x_i}(x', g(x') + s) \, ds \, dx'.~ $$ 定义函数 $v: \mathbb{R}^n \to \mathbb{R}$ 为 $v(x', s) = u(x', g(x') + s)$.根据链式法则，有： $$ v_{x_i}(x', s) = u_{x_i}(x', g(x') + s) + u_{x_n}(x', g(x') + s) \, g_{x_i}(x').~ $$ 但由于 $v$ 具有紧支撑，可以先对 $dx_i$ 积分，从而得到： $$ \int_{\mathbb{R}^{n-1}} \int_{-\infty}^{0} v_{x_i}(x', s) \, ds \, dx' = 0.~ $$ 因此： $$ \begin{aligned} \int_{\mathbb{R}^{n-1}} \int_{-\infty}^{0} u_{x_i}(x', g(x') + s) \, ds \, dx' &= \int_{\mathbb{R}^{n-1}} \int_{-\infty}^{0} -u_{x_n}(x', g(x') + s) \, g_{x_i}(x') \, ds \, dx' \\ &= \int_{\mathbb{R}^{n-1}} -u(x', g(x')) \, g_{x_i}(x') \, dx'. \end{aligned}~ $$ 总结来说，令 $\nabla u = (u_{x_1}, \dots, u_{x_n})$,则有： $$ \int_{\Omega} \nabla u \, dV = \int_{\mathbb{R}^{n-1}} \int_{-\infty}^{g(x')} \nabla u \, dV = \int_{\mathbb{R}^{n-1}} u(x', g(x')) \, (-\nabla g(x'), 1) \, dx'.~ $$ 回忆一下，函数 $g$ 的图像 $\Gamma$ 上某点 $(x', g(x')) \in \Gamma$ 处的外向单位法向量为：$\nu(x', g(x')) = \frac{1}{\sqrt{1 + |\nabla g(x')|^2}} \, (-\nabla g(x'), 1)$,其表面积元为：$dS = \sqrt{1 + |\nabla g(x')|^2} \, dx'$.因此可得： $$ \int_{\Omega} \nabla u \, dV = \int_{\partial \Omega} u \nu \, dS.~ $$ 这就完成了该定理的证明。

对于有边界的紧致黎曼流形

　　 我们要证明如下定理：

　　 定理——设 $\overline{\Omega}$ 是一个具有 $C^2$ 光滑边界的紧致流形，且其度量张量 $g$ 是 $C^1$ 光滑的。记 $\Omega$ 为 $\overline{\Omega}$ 的流形内部，$\partial \Omega$ 为 $\overline{\Omega}$ 的流形边界。记 $(\cdot,\cdot)$ 表示函数的 $L^2(\overline{\Omega})$ 内积，$\langle \cdot,\cdot \rangle$ 表示向量的内积。若 $u \in C^1(\overline{\Omega},\mathbb{R})$，且 $X$ 是 $\overline{\Omega}$ 上的一个 $C^1$ 向量场，则有： $$ (\operatorname{grad} u, X) = -(u, \operatorname{div} X) + \int_{\partial \Omega} u \langle X, N \rangle \, dS,~ $$ 其中，$N$ 是指向 $\partial \Omega$ 外侧的单位法向量。

　　 定理证明\(^\text{[8]}\) 我们采用爱因斯坦求和约定。利用单位分解，可以假设 $u$ 和 $X$ 在某个坐标片 $O \subset \overline{\Omega}$ 内有紧支集。首先考虑该坐标片与 $\partial \Omega$ 不相交的情形。此时，$O$ 可以视为 $\mathbb{R}^n$ 的一个开子集，并且分部积分不会产生边界项： $$ \begin{aligned} (\operatorname{grad} u, X) &= \int_{O} \langle \operatorname{grad} u, X \rangle \sqrt{g} \, dx \\[6pt] &= \int_{O} \partial_j u \, X^j \sqrt{g} \, dx \\[6pt] &= - \int_{O} u \, \partial_j (\sqrt{g} X^j) \, dx \\[6pt] &= - \int_{O} u \, \frac{1}{\sqrt{g}} \partial_j (\sqrt{g} X^j) \, \sqrt{g} \, dx \\[6pt] &= (u, - \frac{1}{\sqrt{g}} \partial_j (\sqrt{g} X^j)) \\[6pt] &= (u, - \operatorname{div} X). \end{aligned}~ $$ 在最后一步等式中，我们使用了 Voss–Weyl 坐标公式来表示散度，尽管前面的恒等式本身也可以用来将 $-\operatorname{div}$ 定义为 $\operatorname{grad}$ 的形式伴随算子。现在假设 $O$ 与 $\partial \Omega$ 相交，则 $O$ 可视为 $\mathbb{R}_+^n = \{x \in \mathbb{R}^n : x_n \ge 0\}$ 的一个开子集。我们将 $u$ 和 $X$ 延拓为在 $\mathbb{R}_+^n$ 上为零，然后进行分部积分，得到： $$ \begin{aligned} (\operatorname{grad} u, X) &= \int_{O} \langle \operatorname{grad} u, X \rangle \sqrt{g} \, dx \\[6pt] &= \int_{\mathbb{R}_+^n} \partial_j u \, X^j \sqrt{g} \, dx \\[6pt] &= (u, -\operatorname{div} X) - \int_{\mathbb{R}^{n-1}} u(x', 0) \, X^n(x', 0) \, \sqrt{g(x', 0)} \, dx', \end{aligned}~ $$ 其中，$dx' = dx_1 \cdots dx_{n-1}$。根据向量场直化定理的一个变式，我们可以选择 $O$，使得 $\frac{\partial}{\partial x_n}$ 方向对应于 $\partial \Omega$ 上的内指单位法向量 $-N$。在这种情况下，有：$\sqrt{g(x', 0)} \, dx' = \sqrt{g_{\partial \Omega}(x')} \, dx' = dS$, 这里的 $dS$ 是 $\partial \Omega$ 上的体积元素。此时，上述公式可以改写为： $$ (\operatorname{grad} u, X) = (u, -\operatorname{div} X) + \int_{\partial \Omega} u \langle X, N \rangle \, dS.~ $$ 至此，定理得证。

5. 推论

　　 通过在散度定理中将 $\mathbf{F}$ 替换为特定形式，可以推导出其他有用的恒等式（参见向量恒等式）。\(^\text{[10]}\)

• 当取 $\mathbf{F} \;\rightarrow\; \mathbf{F}g$ 其中 $g$ 是一个标量函数，$\mathbf{F}$ 是一个向量场时，有： $$ \iiint_{V} \left[\mathbf{F} \cdot (\nabla g) + g (\nabla \cdot \mathbf{F}) \right] \, dV =\iint_{S} g\,\mathbf{F} \cdot \mathbf{n} \, dS .~ $$ 该公式的一个特例是 $\mathbf{F} = \nabla f$，此时该定理就成为格林恒等式的基础。
• 当取 $\mathbf{F} \;\rightarrow\; \mathbf{F} \times \mathbf{G}$（其中 $\mathbf{F}$ 和 $\mathbf{G}$ 是两个向量场，$\times$ 表示叉积）时，有： $$ \iiint_{V} \nabla \cdot (\mathbf{F} \times \mathbf{G}) \, dV = \iiint_{V} \big[ \mathbf{G} \cdot (\nabla \times \mathbf{F}) - \mathbf{F} \cdot (\nabla \times \mathbf{G}) \big] \, dV = \iint_{S} (\mathbf{F} \times \mathbf{G}) \cdot \mathbf{n} \, dS .~ $$
• 当取 $\mathbf{F} \;\rightarrow\; \mathbf{F} \cdot \mathbf{G}$（其中 $\mathbf{F}$ 和 $\mathbf{G}$ 是两个向量场，$\cdot$ 表示点积）时，有： $$ \iiint_{V} \nabla (\mathbf{F} \cdot \mathbf{G}) \, dV = \iiint_{V} \big[ (\nabla \mathbf{G}) \cdot \mathbf{F} + (\nabla \mathbf{F}) \cdot \mathbf{G} \big] \, dV = \iint_{S} (\mathbf{F} \cdot \mathbf{G}) \, \mathbf{n} \, dS.~ $$
• 当取 $\mathbf{F} \;\rightarrow\; f\mathbf{c}$（其中 $f$ 是标量函数，$\mathbf{c}$ 是向量场）时，有：\(^\text{[11]}\) $$ \iiint_{V} \mathbf{c} \cdot \nabla f \, dV = \iint_{S} (f \mathbf{c}) \cdot \mathbf{n} \, dS - \iiint_{V} f (\nabla \cdot \mathbf{c}) \, dV.~ $$ 当 $\mathbf{c}$ 是常向量，或是无散度（即 $\nabla \cdot \mathbf{c} = 0$）的向量场（例如无源无汇的不可压缩流动）时，右侧的第二项为零。特别地，当 $\mathbf{c}$ 为常向量时，有： $$ \iiint_{V} \nabla f \, dV = \iint_{S} f \mathbf{n} \, dS.~ $$
• 当取 $\mathbf{F} \;\rightarrow\; \mathbf{c} \times \mathbf{F}$（其中 $\mathbf{F}$ 是向量场，$\mathbf{c}$ 是常向量）时，有：\(^\text{[11]}\) $$ \iiint_{V} \mathbf{c} \cdot (\nabla \times \mathbf{F}) \, dV = \iint_{S} (\mathbf{F} \times \mathbf{c}) \cdot \mathbf{n} \, dS.~ $$ 将右边的三重积重新排列，并把常向量 $\mathbf{c}$ 提出积分号外，可得： $$ \iiint_{V} (\nabla \times \mathbf{F}) \, dV \cdot \mathbf{c} = \iint_{S} (d\mathbf{S} \times \mathbf{F}) \cdot \mathbf{c}.~ $$ 因此： $$ \iiint_{V} (\nabla \times \mathbf{F}) \, dV = \iint_{S} (\mathbf{n} \times \mathbf{F}) \, dS.~ $$

6. 示例

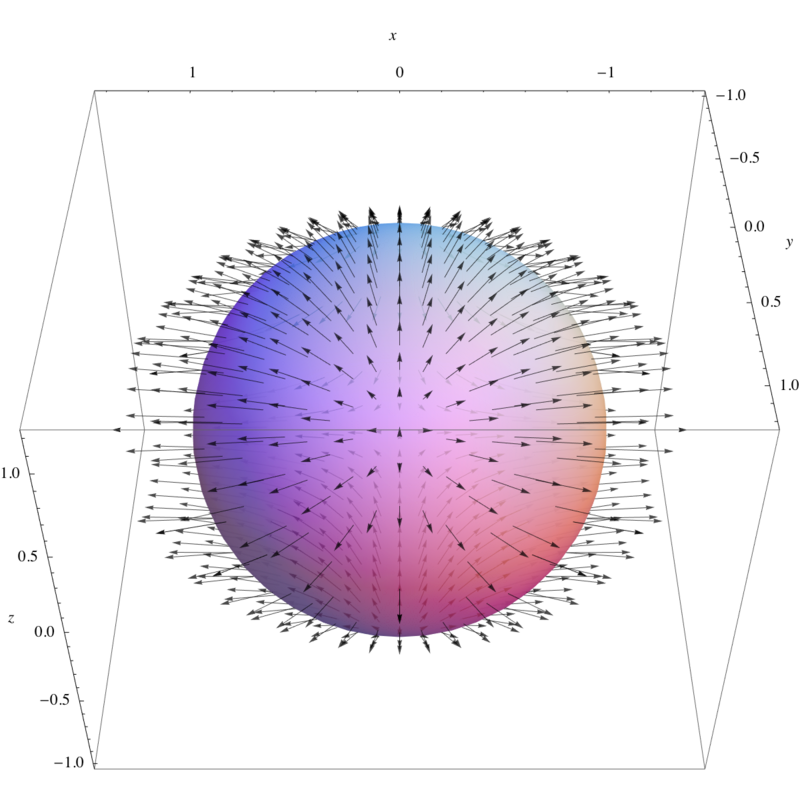
　　 假设我们想要计算 $$ \iint_S \mathbf{F} \cdot \mathbf{n} \, \mathrm{d}S,~ $$ 其中，曲面 $S$ 是单位球面： $$ S = \{ (x, y, z) \in \mathbb{R}^3 : x^2 + y^2 + z^2 = 1 \},~ $$ 而向量场 $\mathbf{F}$ 为： $$ \mathbf{F} = 2x\mathbf{i} + y^2\mathbf{j} + z^2\mathbf{k} .~ $$ 直接计算该曲面积分非常困难，但我们可以利用散度定理简化推导。根据散度定理，该积分等于： $$ \iiint_W (\nabla \cdot \mathbf{F}) \, \mathrm{d}V = 2 \iiint_W (1 + y + z) \, \mathrm{d}V = 2 \iiint_W \mathrm{d}V + 2 \iiint_W y \, \mathrm{d}V + 2 \iiint_W z \, \mathrm{d}V ,~ $$

　　 其中 $W$ 是单位球体： $$ W = \{ (x, y, z) \in \mathbb{R}^3 : x^2 + y^2 + z^2 \leq 1 \}.~ $$ 由于函数 $y$ 在单位球 $W$ 的一个半球内为正，在另一个半球内为负，且数值大小相等方向相反，因此它在整个 $W$ 上的积分为零。同理，$z$ 也是如此： $$ \iiint_W y\,\mathrm{d}V = \iiint_W z\,\mathrm{d}V = 0.~ $$ 因此： $$ \iint_S \mathbf{F} \cdot \mathbf{n} \,\mathrm{d}S = 2 \iiint_W \mathrm{d}V = \frac{8\pi}{3},~ $$ 因为单位球体 $W$ 的体积为 $\frac{4\pi}{3}$。

7. 应用

物理定律的微分形式与积分形式

　　 由于散度定理，许多物理定律都可以同时用微分形式（某个量是另一个量的散度）和积分形式（某个量通过闭合曲面的通量等于另一个量）来表示。典型的例子包括静电学中的高斯定律、磁学中的高斯定律，以及引力中的高斯定律。

连续性方程

　　 （详见：连续性方程） 连续性方程提供了更多同时具有微分形式和积分形式的物理定律示例，而这两种形式正是通过散度定理联系在一起的。在流体力学、电磁学、量子力学、相对论以及许多其他领域，连续性方程用于描述质量、动量、能量、概率或其他物理量的守恒。一般而言，这些方程表明某一守恒量的流动散度等于该量源或汇的分布。散度定理表明，任何这样的连续性方程都可以写成微分形式（基于散度）和积分形式（基于通量）。

平方反比定律

　　 任何平方反比定律都可以改写为类似高斯定律的形式（同时具有微分形式和积分形式，如上所述）。两个典型例子是：静电学中的高斯定律，它源自库仑定律的平方反比形式；以及引力学中的高斯定律，它源自牛顿万有引力定律的平方反比形式。从平方反比公式推导出高斯型方程或反向推导的过程是完全相同的，详细过程可参考这两条定律的相关文献。

8. 历史

　　 约瑟夫·路易·拉格朗日在 1760 年首次引入了曲面积分的概念，并在 1811 年出版的《解析力学》第二版中以更一般的形式再次提出。拉格朗日将曲面积分运用于流体力学研究中 \(^\text{[13]}\)。他在 1762 年发现了散度定理 \(^\text{[14]}\)。

　　 卡尔·弗里德里希·高斯在 1813 年研究椭球体的引力吸引问题时，也使用了曲面积分，并证明了散度定理的若干特殊情况 \(^\text{[15][13]}\)。他在 1833 年和 1839 年又证明了更多特殊情形 \(^\text{[16]}\)。然而，首次对该定理进行一般性证明的人是米哈伊尔·奥斯特罗格拉德斯基，他在 1826 年对热流问题进行研究时给出了完整的推导 \(^\text{[17]}\)。此外，乔治·格林在 1828 年的论文《数学分析在电磁理论中的应用》中 \(^\text{[18][16]}\)，西缅·德尼·泊松在 1824 年关于弹性的论文中，以及弗雷德里克·萨鲁斯在 1828 年关于浮体的研究中 \(^\text{[19][16]}\)，都分别给出了该定理的特殊情况。

9. 已解示例

示例 1

　　 验证平面散度定理在区域 $R$ 上的形式，其中 $$ R = \{(x, y) \in \mathbb{R}^2 : x^2 + y^2 \le 1\},~ $$ 并且向量场为 $$ \mathbf{F}(x, y) = 2y\,\mathbf{i} + 5x\,\mathbf{j}.~ $$ 区域 $R$ 的边界是单位圆 $C$，其参数方程可表示为 $$ x = \cos\left(s\right) , \quad y = \sin\left(s\right) ,~ $$ 其中 $0 \le s \le 2\pi$，参数 $s$ 表示从 $s=0$ 点到圆上某点 $P$ 的弧长。于是，圆 $C$ 的向量方程为 $$ C(s) = \cos\left(s\right) \,\mathbf{i} + \sin\left(s\right) \,\mathbf{j}.~ $$ 在圆 $C$ 上某一点 $P$： $$ P = ( \cos\left(s\right) , \sin\left(s\right) ) \quad \Rightarrow \quad \mathbf{F} = 2 \sin\left(s\right) \,\mathbf{i} + 5 \cos\left(s\right) \,\mathbf{j}.~ $$ 因此： $$ \begin{aligned} \oint_{C} \mathbf{F} \cdot \mathbf{n}\, \mathrm{d}s &= \int_{0}^{2\pi} \left( 2 \sin\left(s\right) \mathbf{i} + 5 \cos\left(s\right) \mathbf{j} \right) \cdot \left( \cos\left(s\right) \mathbf{i} + \sin\left(s\right) \mathbf{j} \right) \,\mathrm{d}s \\[6pt] &= \int_{0}^{2\pi} \left( 2 \sin\left(s\right) \cos\left(s\right) + 5 \sin\left(s\right) \cos\left(s\right) \right) \,\mathrm{d}s \\[6pt] &= 7 \int_{0}^{2\pi} \sin\left(s\right) \cos\left(s\right) \,\mathrm{d}s \\[6pt] &= 0. \end{aligned}~ $$ 因为 $M = \operatorname{Re} (\mathbf{F}) = 2y$ 可得 $\frac{\partial M}{\partial x} = 0$，并且 $N = \operatorname{Im} (\mathbf{F}) = 5x$ 可得 $\frac{\partial N}{\partial y} = 0$.因此： $$ \begin{aligned} \iint_{R} \nabla \cdot \mathbf{F} \,\mathrm{d}A &= \iint_{R} \left( \frac{\partial M}{\partial x} + \frac{\partial N}{\partial y} \right) \,\mathrm{d}A \\[6pt] &= 0. \end{aligned}~ $$

示例 2

　　 假设我们想计算如下向量场的通量：$\mathbf{F} = 2x^2\mathbf{i} + 2y^2\mathbf{j} + 2z^2\mathbf{k}$ 其定义区域由以下不等式所限定： $$ \{0 \leq x \leq 3\},\;\{-2 \leq y \leq 2\},\;\{0 \leq z \leq 2\pi\}.~ $$ 根据散度定理，有： $$ \iiint_{V} \left(\nabla \cdot \mathbf{F}\right)\,\mathrm{d}V = \iint_{S} (\mathbf{F} \cdot \mathbf{n})\,\mathrm{d}S.~ $$ 接下来，我们需要求出向量场 $\mathbf{F}$ 的散度。 如果 $\mathbf{F}$ 是三维向量场，那么其散度为： $$ \nabla \cdot \mathbf{F} = \left( \frac{\partial}{\partial x}\mathbf{i} + \frac{\partial}{\partial y}\mathbf{j} + \frac{\partial}{\partial z}\mathbf{k} \right) \cdot \mathbf{F}.~ $$ 因此，我们可以将该通量积分 $I$ 写作：$I = \iint_{S} \mathbf{F} \cdot \mathbf{n} \,\mathrm{d}S$ 根据散度定理： $$ \begin{aligned} I &= \iiint_{V} \nabla \cdot \mathbf{F} \,\mathrm{d}V \\[6pt] &= \iiint_{V} \left(\frac{\partial F_x}{\partial x} + \frac{\partial F_y}{\partial y} + \frac{\partial F_z}{\partial z}\right)\,\mathrm{d}V \\[6pt] &= \iiint_{V} (4x + 4y + 4z)\,\mathrm{d}V \\[6pt] &= \int_{0}^{3} \int_{-2}^{2} \int_{0}^{2\pi} (4x + 4y + 4z)\,\mathrm{d}V \end{aligned}~ $$ 接下来进行积分计算： $$ \begin{aligned} \int_{0}^{3} \int_{-2}^{2} \int_{0}^{2\pi} (4x + 4y + 4z)\,\mathrm{d}V &= \int_{-2}^{2} \int_{0}^{2\pi} (12y + 12z + 18)\,\mathrm{d}y\,\mathrm{d}z \\[6pt] &= \int_{0}^{2\pi} 24(2z + 3)\,\mathrm{d}z \\[6pt] &= 48\pi (2\pi + 3) \end{aligned}~ $$ 最终结果为： $$ \boxed{ I = \iint_{S} \mathbf{F} \cdot \mathbf{n} \,\mathrm{d}S = 48\pi (2\pi + 3)}~ $$

10. 广义形式

多维情况

　　 可以使用广义斯托克斯定理，将 $n$ 维空间中某一区域 $U$ 内向量场 $\mathbf{F}$ 散度的体积分，与该区域边界 $\partial U$ 上的 $(n-1)$ 维曲面积分建立联系： $$ \underbrace{\int \cdots \int_{U}}_{n} \nabla \cdot \mathbf{F} \, \mathrm{d}V = \underbrace{\oint \cdots \oint_{\partial U}}_{n-1} \mathbf{F} \cdot \mathbf{n} \, \mathrm{d}S~ $$ 该公式也被称为散度定理。

　　 当 $n = 2$ 时，它退化为格林公式。

　　 当 $n = 1$ 时，它进一步简化为微积分基本定理第二部分。

张量场

　　 用爱因斯坦求和约定，可以将散度定理写为： $$ \iiint_V \frac{\partial \mathbf{F}_i}{\partial x_i} \,\mathrm{d}V = \iint_S \mathbf{F}_i n_i \,\mathrm{d}S~ $$ 类似地，将向量场 $\mathbf{F}$ 替换为一个秩 $n$ 的张量场 $T$，可以将公式推广为 \(^\text{[20]}\)： $$ \iiint_V \frac{\partial T_{i_1 i_2 \cdots i_q \cdots i_n}}{\partial x_{i_q}} \,\mathrm{d}V = \iint_S T_{i_1 i_2 \cdots i_q \cdots i_n} n_{i_q} \,\mathrm{d}S~ $$ 其中，每一边至少有一个指标发生了张量缩并。这个公式依然适用于三维空间（即指标 $i_1, i_2, \dots$ 取 $1, 2, 3$），同时它还可以进一步推广到更高或更低的维度，例如在广义相对论中的四维时空中 \(^\text{[21]}\)。

11. 参见

• 开尔文–斯托克斯定理
• 广义斯托克斯定理
• 微分形式

12. 参考文献

1. Katz, Victor J. (1979). “斯托克斯定理的历史”。Mathematics Magazine，52 (3): 146–156. doi:10.2307/2690275. JSTOR 2690275. 收录于 Anderson, Marlow (2009). Who Gave You the Epsilon?: And Other Tales of Mathematical History. Mathematical Association of America, pp. 78–79. ISBN 978-0-88385-569-0.
2. R. G. Lerner; G. L. Trigg (1994). Encyclopaedia of Physics* (第 2 版). VHC. ISBN 978-3-527-26954-9.
3. Byron, Frederick; Fuller, Robert (1992). Mathematics of Classical and Quantum Physics. Dover Publications, p. 22. ISBN 978-0-486-67164-2.
4. Wiley, C. Ray Jr. *Advanced Engineering Mathematics* (第 3 版). McGraw-Hill, pp. 372–373.
5. Kreyszig, Erwin; Kreyszig, Herbert; Norminton, Edward J. (2011). *Advanced Engineering Mathematics* (第 10 版). John Wiley and Sons, pp. 453–456. ISBN 978-0-470-45836-5.
6. Benford, Frank A. (2007 年 5 月). “Notes on Vector Calculus” (PDF). *Math 105: Multivariable Calculus* 课程资料，Prof. Steven Miller 的网页，Williams College. 检索于 2022 年 3 月 14 日.
7. Purcell, Edward M.; Morin, David J. (2013). *Electricity and Magnetism*. Cambridge University Press, pp. 56–58. ISBN 978-1-107-01402-2.
8. Alt, Hans Wilhelm (2016). “Linear Functional Analysis”. *Universitext*. 伦敦: Springer London, pp. 259–261, 270–272. doi:10.1007/978-1-4471-7280-2. ISBN 978-1-4471-7279-6. ISSN 0172-5939.
9. Taylor, Michael E. (2011). “Partial Differential Equations I”. *Applied Mathematical Sciences*, Vol. 115. 纽约, NY: Springer New York, pp. 178–179. doi:10.1007/978-1-4419-7055-8. ISBN 978-1-4419-7054-1. ISSN 0066-5452.
10. Spiegel, M. R.; Lipschutz, S.; Spellman, D. (2009). ector Analysis. Schaum's Outlines (第 2 版). 美国: McGraw Hill. ISBN 978-0-07-161545-7.
11. MathWorld.
12. C.B. Parker (1994). *McGraw Hill Encyclopaedia of Physics* (第 2 版). McGraw Hill. ISBN 978-0-07-051400-3.
13. Katz, Victor (2009). “第 22 章：向量分析”。*A History of Mathematics: An Introduction*. Addison-Wesley, pp. 808–809. ISBN 978-0-321-38700-4.
14. 在他 1762 年关于声学的论文中，拉格朗日研究了散度定理的一个特殊情形：Lagrange (1762) “Nouvelles recherches sur la nature et la propagation du son”（《关于声的本质及传播的新研究》），*Miscellanea Taurinensia*（又名 *Mélanges de Turin*），2: 11–172。该文章后来收入：J.A. Serret（编），*Oeuvres de Lagrange*，巴黎：Gauthier-Villars，1867，第 1 卷，第 151–316 页；在第 263–265 页，拉格朗日通过分部积分将三重积分转化为二重积分。
15. C. F. Gauss (1813). “Theoria attractionis corporum sphaeroidicorum ellipticorum homogeneorum methodo nova tractata”，*Commentationes societatis regiae scientiarium Gottingensis recentiores*，2: 355–378；高斯在文章第 4、5、6 页讨论了该定理的一个特殊情形。
16. Katz, Victor (1979 年 5 月). “A History of Stokes' Theorem”。*Mathematics Magazine*，52 (3): 146–156. doi:10.1080/0025570X.1979.11976770. JSTOR 2690275.
17. 米哈伊尔·奥斯特罗格拉德斯基（Mikhail Ostragradsky）于 1826 年向巴黎科学院提交了他对散度定理的证明；然而，这项工作并未被科学院发表。随后，他返回俄罗斯圣彼得堡，并在 1828 年至 1829 年间向圣彼得堡科学院宣读了他在法国完成的研究工作。该科学院于 1831 年以精简版本刊载了他的研究成果。
    • 他关于散度定理的证明——《Démonstration d'un théorème du calcul intégral》（《积分计算中一个定理的证明》）——最初于 1826 年 2 月 13 日向巴黎科学院宣读，1965 年，这篇论文连同他另一篇文章一起被翻译成俄文并发表。参见：Юшкевич А.П.（A.P. Yushkevich）和 Антропова В.И.（1965）《Неопубликованные работы М.В. Остроградского》（《M.V.奥斯特罗格拉德斯基的未发表著作》），Историко-математические исследования（历史-数学研究），第 16 卷，第 49–96 页；其中包含题为《Остроградский М.В. Доказательство одной теоремы интегрального исчисления》（《M.V.奥斯特罗格拉德斯基：积分计算中一个定理的证明》）的章节。
    • M. Ostrogradsky（宣读时间：1828 年 11 月 5 日；发表时间：1831 年）《Première note sur la théorie de la chaleur》（《关于热理论的第一篇笔记》），发表于圣彼得堡帝国科学院学报，第六辑，第 1 卷，第 129–133 页；其中在 130–131 页可见其散度定理证明的精简版。
    • Victor J. Katz（1979 年 5 月）《The history of Stokes' theorem》（《斯托克斯定理的历史》），发表于 Mathematics Magazine，第 52 卷第 3 期，第 146–156 页（doi:10.1080/0025570X.1979.11976770；2015 年 4 月 2 日存档于 Wayback Machine）。关于奥斯特罗格拉德斯基的散度定理证明，可参阅第 147–148 页。
18. 乔治·格林，*An Essay on the Application of Mathematical Analysis to the Theories of Electricity and Magnetism*（《数学分析在电学与磁学理论中的应用》）（英国诺丁汉：T. Wheelhouse，1838 年）。“散度定理” 的一种形式出现在第 10–12 页。
19. 其他一些早期使用过某种形式的 “散度定理” 的研究者包括：
    • 泊松（Poisson）（宣读时间：1824 年 2 月 2 日；发表时间：1826 年），Mémoire sur la théorie du magnétisme（《磁学理论的备忘录》），法国学术院学报，第 5 卷，第 247–338 页；在第 294–296 页中，泊松将用于计算某一量 $Q$ 的体积分转化为了曲面积分。为了完成这种转换，泊松采用了与证明散度定理相同的方法。
    • 弗雷德里克·萨吕斯（1828 年），Mémoire sur les oscillations des corps flottans（《漂浮物体振荡的备忘录》），纯粹与应用数学年刊（尼姆），第 19 卷，第 185–211 页。
20. K.F. Riley；M.P. Hobson；S.J. Bence（2010 年），Mathematical Methods for Physics and Engineering（《物理与工程的数学方法》），剑桥大学出版社，ISBN 978-0-521-86153-3。
21. 此外，可参考以下文献：J.A. Wheeler；C. Misner；K.S. Thorne（1973 年），Gravitation（《引力论》），W\.H. Freeman & Co.，第 85–86 页，第 3.5 节，ISBN 978-0-7167-0344-0。
    R. Penrose（2007 年），The Road to Reality（《通向实在之路》），Vintage Books，ISBN 978-0-679-77631-4。

13. 外部链接

• “奥斯特罗格拉德斯基公式”，《数学百科全书》，EMS Press，2001 年［1994 年版］
• 微分算子与散度定理，发表于 MathPages
• 散度（高斯）定理，作者 Nick Bykov，Wolfram 演示项目
• Weisstein, Eric W. “散度定理”，MathWorld —— 本文最初基于 PlanetMath 上的 GFDL 文章，链接见：[https://web.archive.org/web/20021029094728/http://planetmath.org/encyclopedia/Divergence.html](https://web.archive.org/web/20021029094728/http://planetmath.org/encyclopedia/Divergence.html)