堆（综述）

贡献者： 待更新

　　 （本文根据 CC-BY-SA 协议转载自原搜狗科学百科对英文维基百科的翻译）

　　 在计算机科学中，堆是一种特殊的基于树的数据结构，本质上是一棵几乎完全的[1]树，它满足堆属性：在最大堆中，对于任意给定的节点 C，如果 P 是 C 的父节点，那么 P 的键（值）大于或等于 C 的键。在最小堆中，P 的键小于或等于 C 的键。堆 “顶部” 的节点（没有父节点）称为根节点。

　　 堆是称为优先队列的抽象数据类型的最有效实现，事实上优先队列通常被称为 “堆”，不管它们是如何实现的。在堆中，最高（或最低）优先级的元素总是存储在根节点。然而，堆不是排序结构，它可以被认为是部分有序的。当需要重复移除优先级最高（或最低）的对象时，堆是一种有用的数据结构。

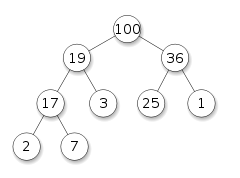
　　 堆的一个常见实现是二叉堆，其中树是二叉树（见图）。堆数据结构，特别是二叉堆，是由 J. W. J. Williams 在 1964 年引入的，作为堆排序算法的数据结构。[2] 堆在一些高效的图算法中也很重要，比如 Dijkstra 算法。当堆是一棵完全二叉树时，它有一个最小的可能高度——一个有 N 个节点的堆，对于每个节点，一个分支总是有 loga N 的高度。

　　 注意，如图所示，兄弟和堂兄弟之间没有隐含的排序，也没有有序遍历的隐含序列（例如，在二叉搜索树中）。上面提到的堆关系仅适用于节点和它们的父亲、祖父等之间。每个节点可以拥有的最大子节点数取决于堆的类型。

1. 操作

　　 涉及堆的常见操作有:

　　 基础

• 查找最大值(或查找最小值):分别查找最大堆的最大项或最小堆的最小项(也称为 peek) 插入:向堆中添加一个新键(也可称 push[3])
• 提取最大值(或提取最小值):从堆中移除节点后，返回最大堆的最大值[或最小堆的最小值](也称为 pop)[4])
• 删除-最大(或删除-最小):分别删除最大堆(或最小堆)的根节点
• 替换:弹出根节点并压入新键。比先进行 pop,后进行 push 更有效，因为只需要平衡一次，而不是两次，并且适合固定大小的堆。[5]

　　 创建

• 创建堆:创建一个空堆
• 堆化:用给定的元素数组创建一个堆
• 合并（merge、union):连接两个堆，形成一个包含两个堆的所有元素的有效新堆，保留原始堆。
• 合并（meld）:连接两个堆，形成一个包含两个堆的所有元素的有效新堆，销毁原始堆。

　　 检查

• 大小（size）:返回堆中的项数。
• 判空（is-empty）:如果堆为空，则返回 true，否则返回 false。

　　 内部的

• 增加键或减少键:分别更新最大堆或最小堆中的键
• 删除:删除任意节点(随后移动最后一个节点并筛选以维护堆)
• 向上筛选:根据需要在树中向上移动一个节点；用于在插入后恢复堆状态。之所以被称为 “筛选”，是因为节点在树中向上移动，直到达到正确的水平，就像在筛子中一样。
• 向下筛选:在树中向下移动一个节点，类似于向上筛选；用于在删除或替换后恢复堆状态。

2. 实现

　　 堆通常在数组(固定大小或动态数组)中实现，并且不需要元素之间的指针。元素插入堆或从堆中删除后，可能会违反堆性质，必须通过内部操作来平衡堆。

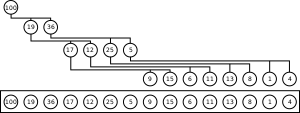
　　 二叉堆可以用单独使用数组的非常节省空间的方式来表示。第一个(或最后一个)元素将包含根元素。数组接下来两个元素包含根元素的孩子。接下来的四个包含两个子节点的四个子节点，等等。因此，在位置 n 的节点的子节点将在以 1 为起点编号数组的 2n 和 2n+1 位置，或者 “以 0 为起点编号数组的 2n+1 和 2n+2 位置。这允许通过简单的索引计算来向上或向下移动树。允许通过向上筛选或向下筛选操作（交换无序元素）来完成平衡堆。因为我们可以从一个数组构建一个堆，而不需要额外的内存(例如，对于节点)，所以 heapsort 可以用来就地排序一个数组。

　　 不同类型的堆以不同的方式实现操作，但值得注意的是，插入通常是通过在堆的末尾第一个可用空间中添加新元素来完成的。这通常会违反堆性质，因此元素会被向上筛选，直到堆性质被重新建立。类似地，删除根元素是通过移动根元素，然后将最后一个元素放入根并向下筛选以重新平衡。因此，替换是通过删除根并将新元素放入根并向下筛选来完成的，和先 pop(向下筛选最后一个元素）,再 push（向上筛选新元素）后相比，避免了向上筛选步骤。

　　 从给定的元素数组中构造二叉(或 d 叉)堆可以使用经典弗洛伊德算法在线性时间内执行，最差情况下的比较次数等于 2N − 2s2(N) − e2(N) (对于二叉堆)，其中 s2(N)是 N 的二进制表示的所有数字的总和，e2(N)是 N 的素数因子分解中的 2 的指数，[6] 这比连续插入原始空堆的序列更快，该操作是对数线性的。

3. 变体

• 2–3 堆
• b 堆
• Beap
• 二进制堆
• 二项式堆
• Brodal 队列
• d-ary 堆
• 斐波那契堆
• 树叶堆
• 左翼堆
• 配对堆
• 基数堆
• 随机可融合堆
• 倾斜堆
• 软堆
• 三元堆
• Treap
• 弱势群体

4. 变体理论界限的比较

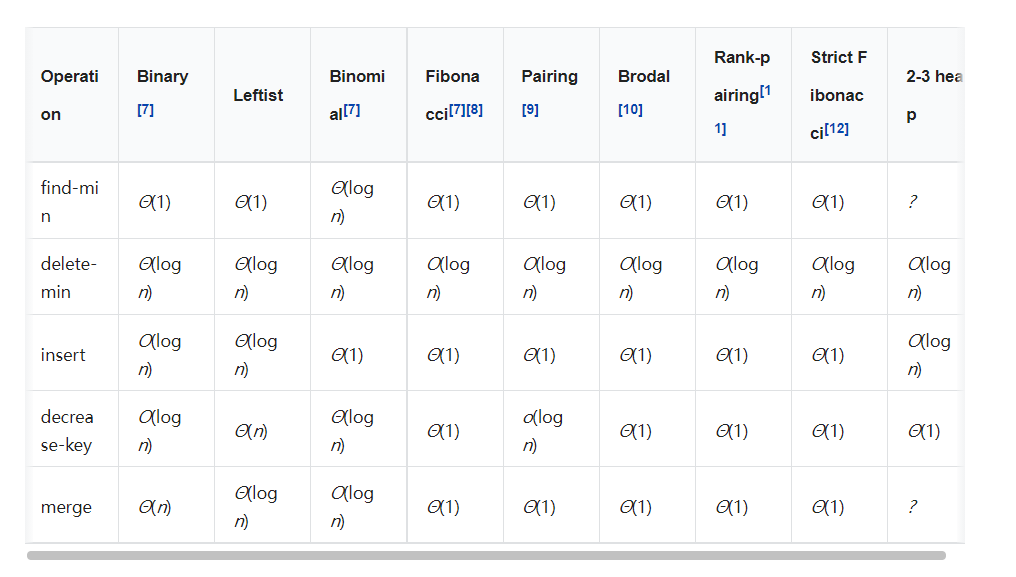
　　 以下是各种堆数据结构的时间复杂度。函数名假设一个最小堆。

　　 In the following time complexities[7] O(f) is an asymptotic upper bound and Θ(f) is an asymptotically tight bound (see Big O notation). Function names assume a min-heap.

1. Each insertion takes $O( \log\left(k\right) )$ in the existing size of the heap, thus $$\sum_{k=1}^N O(\log k).~$$ Since $$\log \frac{n}{2} = (\log n) - 1,~$$ a constant factor (half) of these insertions are within a constant factor of the maximum, so asymptotically we can assume $k = n$; formally the time is $$ n O(\log n) - O(n) = O(n \log n).~$$ This can also be readily seen from Stirling's approximation.
2. Brodal and Okasaki later describe a persistent variant with the same bounds except for decrease-key, which is not supported. Heaps with $n$ elements can be constructed bottom-up in $O(n)$.
3. Amortized time.
4. Lower bound of $\Omega(\log \log n)$, upper bound of $O(2^{2\sqrt{\log \log n}})$.
5. $n$ is the size of the larger heap.

1. 在堆的现有大小中，每次插入的时间复杂度为 $O(\ \log\left(k\right) )$，因此由于这些插入的常数薪资（一半）在最大常数因子内，因此我们可以渐进地假设；形式上的时间是。这也可以从弗斯特林公式中很容易看出。
2. 跳到：$a b c d e f g h i$ 摆平时间
3. $n$ 是较大堆的大小。
4. 下界 上界
5. Brodal 和 Okasaki 后来描述了一个具有相同边界的持久变体，除了 reduce-key，这是不受支持的。具有 $n$ 个元素的堆可以在 $O(n)$ 中自下而上地构建。

5. 应用

　　 堆数据结构有许多应用。

• Heapsort:最好的就地排序算法之一，并且最坏的情况也低于 O(n2)。
• 选择算法:堆允许在常量时间内访问最小或最大元素，其他选择(如中值或第 k 个元素)可以在次线性时间内对堆中的数据进行。[16]
• 图算法:通过使用堆作为内部遍历数据结构，运行时间将按多项式阶减少。这类问题的例子有 Prim 的最小生成树算法和 Dijkstra 的最短路径算法。
• 优先队列(Priority Queue):优先队列是像 “列表” 或 “地图” 这样的抽象概念；正如列表可以用链表或数组来实现一样，优先队列也可以用堆或各种其他方法来实现。
• $k$ 路合并:堆数据结构有助于将许多已经排序的输入流合并成单个排序的输出流。需要合并的例子包括外部排序和来自分布式数据（例如日志结构的合并树）流式结果。内部循环正在获取最小元素，用对应输入流的下一个元素替换，然后执行向下筛选堆操作。(或者替换功能。)(使用优先级队列的提取最大元素和插入函数效率要低得多。)
• 顺序统计:堆数据结构可以用来有效地找到数组中第 k 个最小(或最大)的元素。

6. 实现_F

• C++标准库为堆(通常实现为二叉堆)提供了 make_heap、push_heap 和 pop_heap 算法，这些算法在任意随机访问迭代器上运行。它将迭代器视为对数组的引用，并使用数组到堆的转换。它还提供了容器适配器 priority_queue，它将这些工具包装在一个类似容器的类中。但是，对于替换、向上筛选/向下筛选或减少/增加键操作没有标准支持。
• Boost C++库包括一个堆库。与 STL 不同，它支持减少和增加操作，并支持额外类型的堆:具体来说，它支持 d 叉堆、二项式堆、斐波那契堆、配对堆和斜堆。
• C 和 C++有一个通用的堆实现，支持 D 叉堆和 B-heap。它提供了一个类似 STL 的应用程序接口。
• D 编程语言的标准库包括 std.container.BinaryHeap，它是根据 D 的范围实现的。实例可以从任意随机访问范围构建。二叉堆(BinaryHeap)公开了一个输入范围接口，该接口允许用 D 的内置 foreach 语句进行迭代，并与 std.algorithm 包的基于范围的应用编程接口进行集成。
• java 平台(从 1.5 版开始)提供了一个二叉堆实现，该二叉堆是通过在 Java 集合框架中使用类 java.util.PriorityQueue 来实现。默认情况下，该类实现最小堆；为了实现最大堆，程序员应该编写一个自定义比较器。不支持替换、向上筛选/向下筛选或减少/增加键操作。
• Python 有一个 heapq 模块，它使用二叉堆实现优先队列。该库公开了一个 heapreplace 函数来支持 k 路合并。
• 在标准 PHP 库中，从 5.3 版开始，PHP 同时具有最大堆(SplMaxHeap)和最小堆(SplMinHeap)。
• Perl 在堆分布中实现了二叉堆、二项式堆和斐波那契堆，这些实现的堆可在 CPAN 上获得。
• Go 语言包含一个 heap 包，heap 包中的堆算法在满足给定接口的任意类型上运行。该包不支持替换、向上筛选/向下筛选或减少/增加键操作。
• 苹果的核心基础库包含一个 CFBinaryHeap 结构。
• Pharo 在 Collections-Sequenceable 包中实现了一个堆以及一组测试用例。堆用于定时器事件循环的实现。
• Rust 编程语言在其标准库的 collections 模块中有一个二叉最大堆实现 BinaryHeap。

7. 参考文献

　　 [1] ^CORMEN, THOMAS H. (2009). INTRODUCTION TO ALGORITHMS. United States of America: The MIT Press Cambridge, Massachusetts London, England. pp. 151–152. ISBN 978-0-262-03384-8..

　　 [2] ^Williams, J. W. J. (1964), "Algorithm 232 - Heapsort", Communications of the ACM, 7 (6): 347–348, doi:10.1145/512274.512284.

　　 [3] ^The Python Standard Library, 8.4. heapq — Heap queue algorithm, heapq.heappush.

　　 [4] ^The Python Standard Library, 8.4. heapq — Heap queue algorithm, heapq.heappop.

　　 [5] ^The Python Standard Library, 8.4. heapq — Heap queue algorithm, heapq.heapreplace.

　　 [6] ^Suchenek, Marek A. (2012), "Elementary Yet Precise Worst-Case Analysis of Floyd's Heap-Construction Program", Fundamenta Informaticae, IOS Press, 120 (1): 75–92, doi:10.3233/FI-2012-751..

　　 [7] ^Cormen, Thomas H.（英语：Thomas H. Cormen）; Leiserson, Charles E. ; Rivest, Ronald L. (1990). Introduction to Algorithms (1st ed.). MIT Press and McGraw-Hill. ISBN 0-262-03141-8.CS1 maint: Multiple names: authors list (link).

　　 [8] ^Fredman, Michael Lawrence; Tarjan, Robert E. (July 1987). "Fibonacci heaps and their uses in improved network optimization algorithms" (PDF). Journal of the Association for Computing Machinery. 34 (3): 596–615. doi:10.1145/28869.28874..

　　 [9] ^Iacono, John (2000), "Improved upper bounds for pairing heaps", Proc. 7th Scandinavian Workshop on Algorithm Theory (PDF), Lecture Notes in Computer Science, 1851, Springer-Verlag, pp. 63–77, arXiv:1110.4428, doi:10.1007/3-540-44985-X_5, ISBN 3-540-67690-2.

　　 [10] ^Brodal, Gerth S. (1996), "Worst-Case Efficient Priority Queues" (PDF), Proc. 7th Annual ACM-SIAM Symposium on Discrete Algorithms, pp. 52–58.

　　 [11] ^Haeupler, Bernhard; Sen, Siddhartha; Tarjan, Robert E. (November 2011). "Rank-pairing heaps" (PDF). SIAM J. Computing: 1463–1485. doi:10.1137/100785351..

　　 [12] ^Brodal, G. S. L.; Lagogiannis, G.; Tarjan, R. E. (2012). Strict Fibonacci heaps (PDF). Proceedings of the 44th symposium on Theory of Computing - STOC '12. p. 1177. doi:10.1145/2213977.2214082. ISBN 9781450312455..

　　 [13] ^Goodrich, Michael T.; Tamassia, Roberto (2004). "7.3.6. Bottom-Up Heap Construction". Data Structures and Algorithms in Java (3rd ed.). pp. 338–341. ISBN 0-471-46983-1..

　　 [14] ^Fredman, Michael Lawrence (July 1999). "On the Efficiency of Pairing Heaps and Related Data Structures" (PDF). Journal of the Association for Computing Machinery. 46 (4): 473–501. doi:10.1145/320211.320214..

　　 [15] ^Pettie, Seth (2005). Towards a Final Analysis of Pairing Heaps (PDF). FOCS '05 Proceedings of the 46th Annual IEEE Symposium on Foundations of Computer Science. pp. 174–183. CiteSeerX 10.1.1.549.471. doi:10.1109/SFCS.2005.75. ISBN 0-7695-2468-0..

　　 [16] ^Frederickson, Greg N. (1993), "An Optimal Algorithm for Selection in a Min-Heap", Information and Computation (PDF), 104 (2), Academic Press, pp. 197–214, doi:10.1006/inco.1993.1030.