电磁相互作用
贡献者: 待更新
(本文根据 CC-BY-SA 协议转载自原搜狗科学百科对英文维基百科的翻译)
电磁学是物理学的一个分支,是对电磁力这种发生在带电粒子之间的物理相互作用的研究。电磁力由电场和磁场所组成的电磁场所介导,它也对电磁辐射(例如可见光)负责,是自然中四种基本互相作用(通常被称为力)之一。其他三种基本相互作用是强相互作用、弱相互作用和万有引力。[1]在高能量下,弱力和电磁力被统一为单一的弱电力。
电磁现象是根据电磁力来定义的(后者有时也被称为洛伦兹力),包括电和磁作为同一现象的不同表现形式。电磁力在决定日常生活中遇到的大多数物体的内部性质方面起着重要作用。原子核和它们的轨道电子之间的电磁吸引力使得原子保持一个整体的状态。电磁力负责原子之间的化学键(分子的成因)和分子间作用力。电磁力控制着所有的化学过程,这些化学过程来源于相邻原子中的电子之间的相互作用。
存在很多电磁场的数学描述。在经典电动力学中,电场被描述为电势和电流。在法拉第定律中,磁场与电磁感应和磁性相关联。麦克斯韦方程组描述了电场和磁场是如何由彼此以及电荷和电流所产生和改变的。
电磁学的理论结果(特别是基于传播 “介质” 的性质(磁导率和电容率)所建立的光速)导致了阿尔伯特·爱因斯坦于 1905 年对狭义相对论的发展。
1. 理论的历史
最初,电与磁被认为是两种独立的力。然而,詹姆斯·克拉克·麦克斯韦于 1873 年出版的《电与磁论文集》改变了物理学家们的这一观点。在麦克斯韦的著作中,正电荷和负电荷的相互作用被证明是由一种力所介导的。这些相互作用产生了四种主要效应,所有这些都已经被实验清楚地证明了:
- 电荷之间的互相吸引或者排斥是通过一种反比于它们之间距离平方的力:异种电荷相互吸引,同种电荷相互排斥。
- 磁极(或单个点的极化状态)以类似正电荷和负电荷的方式相互吸引或排斥,并且总是成对存在:每个北极都与一个南极相连。
- 电线内部的电流在电线外部产生相应的圆周磁场。它的方向(顺时针或逆时针)取决于导线中电流的方向。
- 当线圈朝向或远离磁场移动或者磁体朝向或远离线圈移动时,电流便在线圈中产生;电流的方向取决于运动方向。
在准备 1820 年 4 月 21 日晚上的演讲时,汉斯·克里斯蒂安·奥斯特做了一个令人惊讶的观察。当他准备材料时,他注意到一个指南针偏离了磁北极,这发生在他使用的电池的电流被打开和关闭时。这种偏转使他相信磁场从携带电流的电线的所有侧面辐射出来,就像光和热一样,并且它证实了电与磁之间的直接关系。
在做出这个发现时,奥斯特没有对这一现象提出任何令人满意的解释,也没有试图用数学框架来表示这一现象。然而,三个月后,他开始了更深入的调查。此后不久,他发表了他的发现,证明电流在流经导线时会产生磁场。磁感应的 CGS 单位(奥斯特)就是为了纪念他对电磁学领域的贡献而命名的。
他的发现导致了整个科学界对电动力学的深入研究。在它们的影响下,法国物理学家安德烈·玛丽·安培发展了一种单一的数学形式来表示载流导体之间的磁力。奥斯特的发现也是迈向一个统一的能量概念的重要一步。
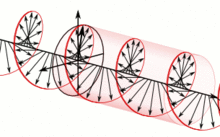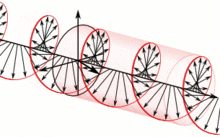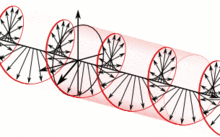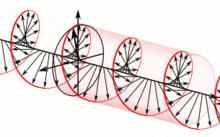
这种统一由法拉第观察到,被詹姆斯·克拉克·麦克斯韦所扩展,并由奥利弗·亥维赛和海因里希·赫兹部分地重新表述,是 19 世纪数学物理的主要成就之一。[2]它产生了深远的影响,其中之一是对光的本质的理解。与当时电磁理论所提出的不同,光和其他电磁波目前被认为是量子化的自主传播的振动的电磁场扰动,被称为光子。不同的频率振荡产生不同形式的电磁辐射,从最低频率的无线电波,到中等频率的可见光,再到最高频率的γ射线。
奥斯特不是唯一一个研究电与磁关系的人。在 1802 年,意大利法律学者吉安·多梅尼科·罗马诺西用伏打电堆偏转了一根磁针。实验的实际设置还不完全清楚,我们也不知道电流是否有流过磁针。1802 年,一家意大利报纸发表了对这一发现的报道,但它在很大程度上被当时的科学界所忽视,因为罗马诺西似乎不属于这个群体。[3]
库克森博士报告了早期(1735 年)电与磁之间经常被忽视的一个联系。[4]他的描述说道:“约克郡维克菲尔德的一个商人在一个大箱子里放了很多刀叉...把盒子放在一个大房间的角落后,突然出现了雷电交加的暴风雨...店主倒空了放着钉子的柜台上的盒子,拿起放在钉子上的刀子的人注意到刀子带起了钉子。所有刀子都被拿来试了,人们发现它们做着同样的事情,吸起了大钉子、包装针和其他重量相当大的铁制品...” 惠特克尔在 1910 年提出这一特殊事件导致闪电 “被认为是磁化钢的力量;毫无疑问,正是这一点导致富兰克林在 1751 年试图通过排放莱顿瓶来磁化缝针。”[5]
2. 基本力
电磁力是四种已知的基本力之一。其他基本力是:
- 弱核力,它作用于标准模型中的所有已知粒子,并导致某些形式的放射性衰变。(然而在粒子物理学中,电弱相互作用是自然界四种已知基本相互作用中的两种的统一描述:电磁相互作用和弱相互作用);
- 强核力,它使得夸克形成核子,并使得核子形成原子核;
- 万有引力。
所有其他力(例如摩擦力和接触力)都来源于这四种基本力(包括粒子运动所携带的动量)。[6]
除了重力之外,电磁力几乎是人们日常生活中遇到的所有超出原子核尺度的现象的原因。粗略地说,所有参与原子间相互作用的力可以用带电的原子核和原子的电子之间的电磁力来解释。电磁力也解释了这些粒子如何通过运动来携带动量。这包括我们在 “推” 或 “拉” 普通物质对象时所体验到的力,这种力来自于作用在我们的身体和物体中的单独的分子之间的分子间作用力。电磁力也涉及到所有形式的化学现象。
理解原子内和分子间的力的一个必要部分是电子运动动量所产生的有效力,这样当电子在相互作用的原子之间运动时会携带动量。随着电子集合变得更加受限,它们的最小动量必然由于泡利不相容原理而增加。物质在分子尺度上的行为(包括密度)是由电磁力和电子自身动量交换所产生的力之间的平衡决定的。[7]
3. 经典电动力学
1600 年,威廉·吉尔伯特在他的《De Magnete》一书中提出电与磁虽然都能引起物体的吸引和排斥但却是截然不同的效应。水手们已经注意到雷击有干扰指南针的能力。直到本杰明·富兰克林在 1752 年提出的实验之后,闪电和电之间的联系才得到证实。最早发现和发表人造电流和磁性之间的联系的人之一是罗马诺西,他在 1802 年注意到在伏打电堆两端连接一根电线会偏转附近的指南针。然而,直到 1820 年奥斯特进行了类似的实验以后,这种效应才广为人知。[8]奥斯特的工作影响了安培,后者在数学基础上建立了电磁学理论。
一个被称为 “经典电磁学” 的电磁学理论由不同的物理学家在 1820 年至 1873 年期间发展起来,并最终由完善于詹姆斯·克拉克·麦克斯韦的论文,后者将前面的发展统一为一个单一的理论,并发现了光的电磁本质。[9]在经典电磁学中,电磁场的行为由一组称为麦克斯韦方程组的方程所描述,电磁力则由洛伦兹力定律给出。[10]
经典电磁学的一个特点是很难与经典力学协调一致,但它与狭义相对论兼容。根据麦克斯韦方程组,真空中的光速是一个普适常数,它仅取决于真空的电容率和磁导率。这违反了作为经典力学的长期基石的伽利略不变性。调和这两种理论(电磁学和经典力学)的一种方法是假设一种称为以太的光传播介质的存在。然而,随后的实验努力未能探测到以太的存在。在亨德里克·洛伦兹和儒勒·昂利·庞加莱做出重要贡献之后,1905 年阿尔伯特·爱因斯坦通过引入狭义相对论解决了这个问题,用与经典电磁学兼容的新运动学理论取代了经典运动学。(如需更多资讯,请参阅狭义相对论发现史)
此外,相对论意味着在运动参考系中磁场可以转换得到非零的电场,反之,运动的电场可以转换得到非零的磁场,从而强有力地表明这些现象是同一枚硬币的两面。因此有了 “电磁学” 这个术语。(有关更多信息,请参见经典电磁学和狭义相对论以及经典电磁理论的协变形式)
4. 非线性现象的扩展
麦克斯韦方程组是线性的,源(荷和流)的变化导致场的成比例变化。非线性动力学可以出现于电磁场与遵循非线性动力学定律的物质耦合时。这是研究,例如,在磁流体力学中就有相关研究,这个学科将麦克斯韦理论和纳维-斯托克斯方程结合在了一起。
5. 物理量和单位
电磁单位是主要基于电流的磁性性质的电气单位系统的一部分,基本的国际单位是安培。这些单位是:
- mpere (电流)
- coulomb (电荷)
- farad (电容)
- henry (电感)
- ohm (电阻)
- siemens (电导)
- tesla (磁通密度)
- volt (电势)
- watt (功率)
- weber (磁通量)
在电磁 CGS 系统中,电流是通过安培定律定义的基本量,并以磁导率为无量纲量(相对磁导率),其在真空中的值为 1。因此,光速的平方在联系起这个系统中的物理量的一些方程中显式出现。
| Symbol[11] | Name of quantity | Unit name | Symbol | Base units |
| Q | electric charge | coulomb | C | A⋅s |
| I | electric current | ampere | A | A (= W/V = C/s) |
| J | electric current density | ampere per square metre | A/$m^2$ | A⋅$m^{-2}$ |
| U,$\Delta v$,$\Delta \varphi$,E | potential difference; electromotive force | volt | V | $J/C$ = $kg$⋅$m^2$⋅$s^{-3}$⋅$A^{-1}$ |
| R,Z,X | electric resistance; impedance; reactance | ohm | $\Omega$ | $V/A$ = $kg$⋅$m^2$⋅$s^{-3}$⋅$A^{-2}$ |
| $\rho$ | resistivity | ohm metre | $\Omega $⋅$m$ | $kg$⋅$m^3$⋅$s^{-3}$⋅$A^{-2}$ |
| P | electric power | watt | W | $V$⋅$A$= $kg$⋅$m^2$⋅$s^{-3}$ |
| C | capacitance | farad | F | $ C/V $= $kg^{-1}$⋅$m^{-2}$⋅$A^2.s^4 $ |
| $\Phi_E$ | electric flux | volt metre | $V$⋅$m$ | $kg$⋅$m^3$⋅$s^{-3}$⋅$A^{-1}$ |
| E | electric field strength | volt per metre | V/m | $N/C$ = $kg$⋅$m$⋅$A^{-1}$⋅$s^{-3}$ |
| D | electric displacement field | coulomb per square metre | C/$m^2$ | $A$⋅$s$⋅$m^{-2}$ |
| $\varepsilon$ | permittivity | farad per metre | F/m | $ kg^{-1}$⋅$m^{-3}$⋅$A^2$⋅$s^4$ |
| $\chi_e$ | electric susceptibility | (dimensionless) | 1 | 1 |
| $G,Y,B$ | conductance; admittance; susceptance | siemens | S | $\Omega^{-1} $= $kg^{-1}$⋅$m^{-2}$⋅$^s3$⋅$A^2$ |
| K,Y,$\sigma$ | conductivity | siemens per metre | $S/m$ | $kg^{-1}$⋅$m^{-3}$⋅$s^3$⋅$A^2$ |
| B | magnetic flux density, magnetic induction | tesla | T | $Wb/m^2$ = $kg$⋅$s^{-2}$⋅$A^{-1}$ = $N$⋅$A^{-1}$⋅$m^{-1}$ |
| $\Phi,\Phi_M,\Phi_B$ | magnetic flux | weber | Wb | $ V$⋅$s$ = $kg$⋅$m^2$⋅$s^{-2}$⋅$A^{-1}$ |
| H | magnetic field strength | ampere per metre | A/m | $A$⋅$m^-1$ |
| L, M | inductance | henry | H | $Wb/A$ = $V$⋅$s/A $= $kg$⋅$m^2$⋅$s^{-2}$⋅$A^{-2}$ |
| $\mu$ | permeability | henry per metre | $H/m$ | $kg$⋅$m$⋅$s^{-2}$⋅$A^{-2}$ |
| $\chi$ | magnetic susceptibility | (dimensionless) | 1 | 1 |
电磁学物理定律的公式(例如麦克斯韦方程组)需要根据使用的单位系统进行调整。这是因为国际单位制中的电磁单位和厘米-克-秒制中的电磁单位之间没有一一对应关系,正如机械单位的情况一样。此外,在 CGS 中,电磁单位有几种合理的选择,它们导向不同的单位 “子系统”,包括高斯单位、“ESU”、“EMU” 和亥维赛-洛伦兹单位。在这些选择中,高斯单位制是当今最常见的,事实上,“CGS 单位” 一词经常被用来特指 CGS-高斯单位制。
参考文献
[1]Ravaioli, Fawwaz T. Ulaby, Eric Michielssen, Umberto (2010). Fundamentals of applied electromagnetics (6th ed.). Boston: Prentice Hall. p. 13. ISBN 978-0-13-213931-1..
[2]Darrigol, Olivier (2000). Electrodynamics from Ampère to Einstein. New York: Oxford University Press. ISBN 0198505949..
[3]Martins, Roberto de Andrade. "Romagnosi and Volta's Pile: Early Difficulties in the Interpretation of Voltaic Electricity" (PDF). In Fabio Bevilacqua and Lucio Fregonese (eds). Nuova Voltiana: Studies on Volta and his Times. vol. 3. Università degli Studi di Pavia. pp. 81–102. Archived from the original (PDF) on 2013-05-30. Retrieved 2010-12-02.CS1 maint: Uses editors parameter (link).
[4]八.闪电在交流磁性方面的非凡作用的描述。由约克郡维克菲尔德的库克森博士的医学博士皮尔斯·多德传播。菲尔。Trans。1735 39,74-75,发表于 1735 年 1 月 1 日.
[5]惠特克,E.T. (1910)。笛卡尔到十九世纪末以太和电理论的历史。朗曼、格林和公司。.
[6]布朗,《工程和科学物理学》,第 160 页:“重力是自然的基本力量之一。摩擦力、张力和法向力等其他力来自电力,这是另一种基本力。重力是一种相当弱的力...两个质子之间的电力比它们之间的重力强得多。”.
[7]珀塞尔,“电与磁,第三版”,第 546 页:第 11 章第 6 节,“电子自旋和磁矩”.
[8]Stern, Dr. David P.; Peredo, Mauricio (2001-11-25). "Magnetic Fields – History". NASA Goddard Space Flight Center. Retrieved 2009-11-27..
[9]珀塞尔,第 436 页。第 9.3 章,“麦克斯韦对电磁场的描述基本上是完整的。”.
[10]珀塞尔:第 278 页:第 6.1 章,“磁场的定义” 洛伦兹力和力方程。.
[11]国际纯化学和应用化学联合会 (1993). Quantities, Units and Symbols in Physical Chemistry, 2nd edition, Oxford: Blackwell Science. ISBN 0-632-03583-8. pp. 14–15. Electronic version..
友情链接: 超理论坛 | ©小时科技 保留一切权利