无碰撞暗物质的引力坍缩

贡献者：周思益

　　暗物质星系晕的形成是一个概念上定义得很好的理论问题：从一个由无碰撞和无耗散体组成的大致球形轻微过密区域开始，并让它在重力作用下演化。系统开始在自己的重量下坍缩（在某个时刻，不均匀性增长超出了可计算的线性近似），但坍缩自我限制，没有达到无限密度的点。这是因为暗物质是无碰撞的，不能耗散能量，所以在坍缩过程中，它的引力势能必须转化为涉及的暗物质粒子的动能。球体最终放松到一个自重力准静态结构，由暗物质粒子的随机运动支撑。整个过程被称为位力化，产生的系统是位力化的，即其能量在势能 $V$ 和动能 $K$ 之间分布，符合位力定理 $\langle K\rangle = -1/2 \langle V\rangle $。

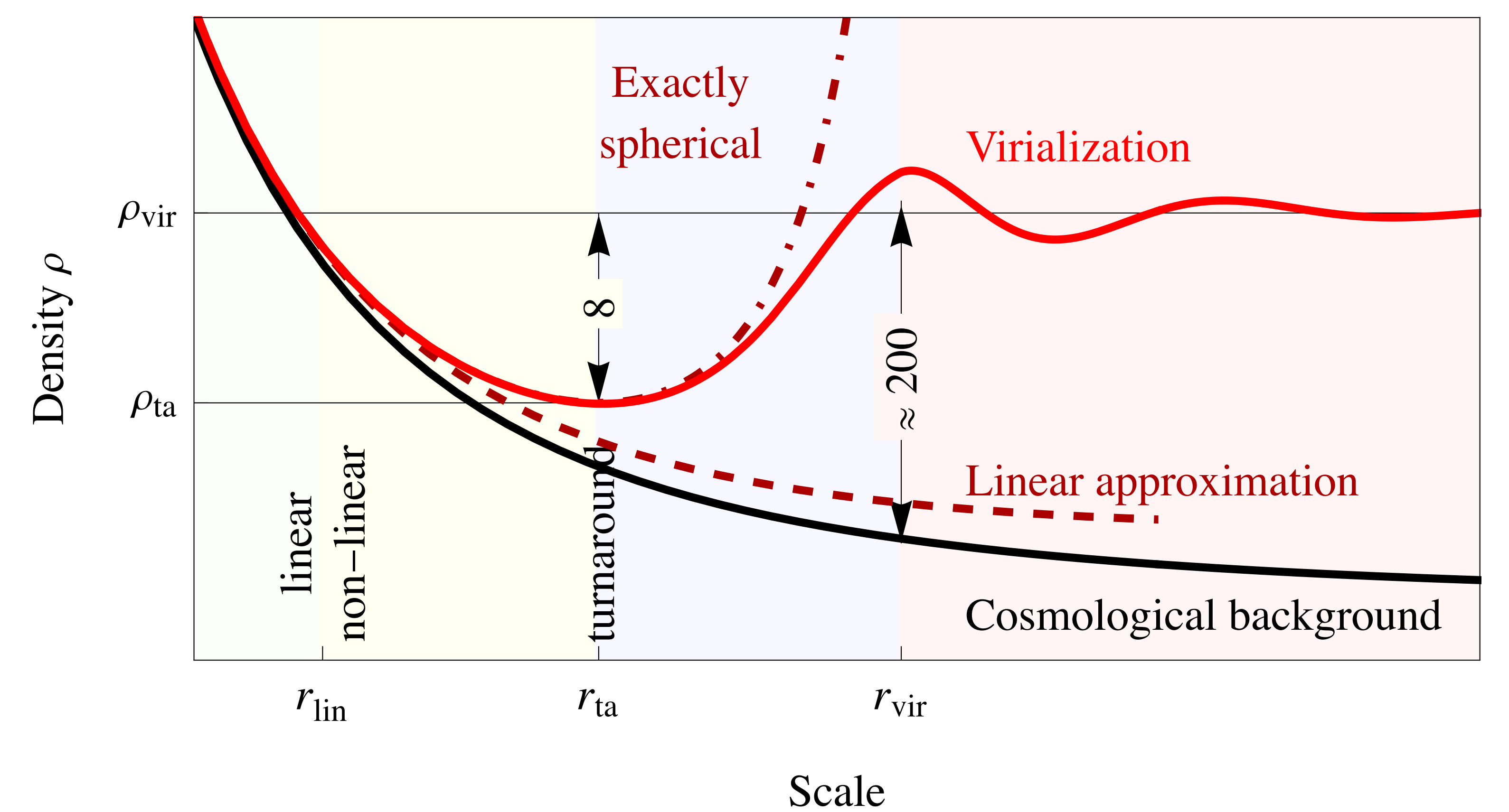
　　位力定理提供了足够的信息来估计涉及的典型尺度。为了简化，我们考虑一个具有均匀密度的球形暗物质过密区域，其总质量为 $M_{tot}$（也在文献中考虑了具有非恒定密度的椭球形坍缩模型）。下面讨论的主要阶段如图 1 所示。

图 1

　　我们定义 $\rho_{ta}$ 为在转折点(turn around,缩写为 ta)的均匀密度，即过密区域停止跟随由大爆炸引起的膨胀，停滞并开始坍缩成一个受引力束缚的物体的时刻。这标志着结构形成的开始。由于暗物质正在停滞，它的动能 $K_{ta}$ 消失，因此它的总能量 $E_{ta} = K_{ta} + V_{ta}$ 完全由它的引力势能决定：

\begin{equation} V_{\text{ta}} = - G \int_0^{r_{ta}} \bigg( \frac{4\pi r^3}{3} \rho_{in} \bigg) \frac{4\pi r^2 dr \rho_{ta}}{r} = -\frac{3}{5} \frac{G M_{\text{tot}}^2}{r_{\text{ta}}} ~. \end{equation}

其中 $r_{ta}$ 是球体在转折点的大小，$\rho_{in}$ 是球体内部的密度（在我们的近似中取为 $\rho_{ta}$）。如果球对称性绝对精确，即如果所有暗物质粒子都遵循完美的径向轨迹，坍缩将朝着无限密度发展，形成黑洞。实际上，系统平均保持球形，并且由于暗物质粒子的混沌运动（它们只通过重力相互作用），达到了有限的密度。在这个位力化过程之后，能量在动能和势能之间分布，使得 $E_{vir} = K_{vir} + V_{vir} = V_{vir}/2$，最后一个等式遵循位力定理。由于位力化保持总能量守恒，势能 $V_{vir} = -3GM^2_{tot}/5r_{vir}$（我们仍然近似密度为常数，$\rho_{vir} = M_{tot}/(4/3\pi r^3_{vir}$)，现在 $r_{vir}$ 是位力化晕的半径），因此意味着 $r_{vir} = r_{ta}/2$。也就是说，坍缩导致了一个松弛的晕，其大小是转折点泡沫的一半，密度大约是其 8 倍，$\rho_{vir} = 8\rho_{ta}$。¹

　　形成的晕的平均密度 $\rho_{\text{vir}}$ 大致是周围宇宙密度 $\bar{\rho}$ 的 200 倍：

\begin{equation} \rho_{\text{vir}} \approx 200 \bar{\rho} = \frac{3H^2}{8\pi G} = \frac{1}{6\pi G t^2_{\text{vir}}}~. \end{equation}

其中 $t_{\text{vir}}$ 是位力化结束的时间标记(假设物质主导）。位力半径就是这样定义的：在维里半径内晕的平均密度是宇宙密度的 $200$ 倍，记作 $r_{200}$。在 $r_{200}$ 内的总质量被视为晕的总质量的度量。实际上，至少在数值模拟中看到的更为复杂，但数量级是正确的。

　　除了其全局属性外，我们可以通过分析坍缩并特别关注松弛机制来获得对最终暗物质晕（特别是我们在这里感兴趣的其密度和速度分布）稍微更精细的理解。有几个这样的动力学过程在起作用，推动系统达到平衡配置。对于无碰撞暗物质粒子来说，重要的机制是所谓的暴力松弛：由于暗物质粒子本身产生的引力势也在随着持续的坍缩而变化，因此一个暗物质粒子的能量随时间变化。这种机制在坍缩的短时间尺度上有效，因此得名 “暴力”。如果引力势是时间依赖的，那么给定暗物质粒子的总能量除以其质量，$\varepsilon = v^2/2 + \varphi$，随时间的变化为 $d\varepsilon/dt = \partial\varphi/\partial t$。这个最后的关系很容易验证：

\begin{equation} \frac{d\varepsilon}{dt} = \frac{\partial\varepsilon}{\partial v} \cdot \frac{dv}{dt} + \frac{\partial\varepsilon}{\partial\varphi} \cdot \frac{d\varphi}{dt} = v \cdot (-\nabla\varphi) + \bigg(\frac{\partial\phi}{\partial t} + v \cdot \nabla\phi \bigg) = \frac{\partial\varphi}{\partial t}~. \end{equation}

其中等式很容易从链式法则、$\varepsilon$ 的定义以及 $dv/dt = -\nabla\varphi$ 得出，这是牛顿定律 $a = F/m$ 在仅有引力相互作用的情况下的形式。一个粒子是获得还是失去能量是一个复杂问题。通过考虑一个从晕的外围开始坍缩的暗物质粒子，可以定性地弄清楚发生了什么（它本身将首先坍缩然后扩展，直到粒子达到位力化）。在下落过程中，暗物质粒子将潜入由于坍缩的晕而形成的深势中并增加动能。穿过中心点（由于其无碰撞特性而未受伤害）后，它将爬出一个更浅的势，因为其同伴暗物质粒子正在分散，因此将花费少于之前获得的动能，导致净能量增加。对于从内部位置开始的粒子则相反。例如，一个在中心静止的粒子不会移动，而当原晕坍缩时，其中心的势变得更深。通常，单个粒子的能量增加或减少以一种复杂的方式取决于其初始位置和初始速度，以及所有其他暗物质的分布。

　　整个过程实际上相当于暗物质粒子经历许多引力相互作用。因此，它们的最终速度是由许多随机贡献的总和给出的。由于中心极限定理，它们的能量分布将趋向于高斯分布：

\begin{equation} f(\varepsilon) = \frac{n_0}{(2\pi\sigma^2)^{3/2}} e^{-\varepsilon/\sigma^2} ~. \end{equation}

其中乘以指数的奇异归一化因子的形式很快就会清楚。指数是 $\varepsilon = \frac{1}{2}v^2 + \varphi$，由此可以立即得出能量分布 $f(\varepsilon)$ 可以被解释为暗物质速度的分布 $f(v)$，呈现为麦克斯韦-玻尔兹曼形式：

\begin{equation} f(v) \propto e^{-v^2/2\sigma^2}~. \end{equation}

对于一个完全位力化的晕，均匀的 “温度”（与速度分散σ有关）由其总质量给出。为了证明这一点，我们接下来讨论暗物质密度分布 $\rho(r)$。对于球对称系统，$f(v)$ 和 $\rho(r)$ 之间存在一个唯一的对应关系（这种一般关系被称为爱丁顿公式，从 $f(v)$ 导出 $\rho(r)$ 称为爱丁顿反演）。它可以通过首先对所有速度积分 $f(\varepsilon)$ 来推导²，然后得到暗物质密度分布的隐式表达式：

\begin{equation} \rho = M \int_0^\infty dv \, 4\pi v^2 f(\varepsilon) = M \int_0^\infty dv \, 4\pi v^2 \frac{n_0}{(2\pi\sigma^2)^{3/2}} e^{-(v^2/2+\varphi)/\sigma^2} = \rho_0 e^{-\varphi/\sigma^2}~. \end{equation}

其中 $\rho_0 = Mn_0$。式 6 以 $\rho$ 的形式给出引力势。将这个表达式代入泊松方程 $\nabla^2\varphi = 4\pi G\rho$，写成球坐标形式，得到：

\begin{equation} \frac{d}{dr} \left( r^2 \frac{d}{dr} \ln\rho \right) = -4\pi G \frac{\sigma^2}{r^2} \rho~. \end{equation}

解是：

\begin{equation} \rho(r) = \frac{\sigma^2}{2\pi G} \frac{1}{r^2}~. \end{equation}

图 2：子晕。N 体模拟发现暗物质形成一个大致球形的晕，然后被许多更小的子晕所包围和填充。来自 Millennium-XXL 模拟。

　　这种分布是奇异等温球体。这个名字来自于这样一个事实：这是理想气体通过碰撞和相互作用达到的平衡配置，其特征是单一的与半径无关的温度 T。在这里，“碰撞和相互作用” 的角色由暗物质粒子与整个晕之间的引力散射扮演，其有效截面由下式给出：

\begin{equation} \sigma_{\text{grav}} = \frac{G M_{\text{tot}} M}{r^2 v^4}~. \end{equation}

在我们的情况下，与半径恒定的量是速度分散 $\sigma$：如果将 $\sigma^2$ 识别为 $ k_{\text{B}} T/M $，其中 $ k_{\text{B}} $ 是玻尔兹曼常数，那么我们就实现了与理想气体情况的对应。

　　总结来说，关于孤立、球形、无碰撞和无耗散系统坍缩的经典理论预测了达到平衡的暗物质晕是具有完全麦克斯韦-玻尔兹曼速度分布的奇异等温球体。这通常被称为标准晕模型（SHM）。

　　实际上，奇异等温模型只是一个理想化的近似。它的密度在 $ r \to 0 $ 时发散，但这不是一个严重的问题，因为包含在半径 $r$ 内的总质量是有限的，$ M(r) = \int_0^r dr 4\pi r^2 \rho = \frac{2\sigma^2 r}{G} $。得到的旋转曲线完全平坦，$ v_{\text{circ}}^2(r) = \frac{G M(r)}{r} = 2\sigma^2 $。另一方面，积分到大半径时，总质量发散，这从天体物理学的角度来看是荒谬的：因此，这个分布表必须在某个大半径处被修正和截断。更一般地说，许多效应可能导致偏离导致等温分布的简单图景：

　　 (i) 坍缩过程可能是不完整的，没有达到完全平衡状态，

　　 (ii) 球对称性的假设很容易被初始条件中的非径向变形所违反，

　　 (iii) 系统是孤立的假设对于嵌入暗物质宇宙网中的晕来说不是有效的：通常不能忽略流入、流出和合并等。标准晕模型可以扩展以纠正其中的一些缺陷，使其更加现实，尽管这通常以更复杂的分析处理为代价。鉴于这些复杂性和纯分析方法的局限性，数值模拟已经成为确定暗物质晕属性的重要工具。

1. 来自 N 体模拟的结果

　　由于统计力学没有提供明确的一般性答案，暗物质的引力坍缩也通过 $N$ 体模拟进行了数值研究，我们已经介绍了这些模拟。虽然这些计算机代码不模拟特定的星系（我们特别感兴趣的是银河系或当地的矮星系），而是模拟了一个或多或少典型的星系集合，但它们的结果显示暗物质晕的密度分布倾向于拥有一些通用特征，如下所述。

　　暗物质晕的尺寸跨越所有模拟尺度：从大约 $100 Mpc$ 的宇宙学尺度到数十 $pc$ 的亚星系尺度，质量范围大约有 $20$ 个数量级。晕的数量 $ n $ 作为它们质量的函数大致按照 $ dn/dM \propto 1/M^2 $ 的比例变化，将进行分析。

　　首先，发光物质大致遵循大尺度结构的分布，即星系形成于物质密集的地方。然而，星系并不完全追踪底层的暗物质分布，因为星系形成的效率取决于晕的质量。星系的平均过密度 $ \delta_{\text{gal}} $ 与总质量的平均过密度 $ \delta_{\text{tot}} $（主要由暗物质主导）之间的关系是复杂的。它们的比值，即所谓的偏差 $ b =\delta_{\text{gal}}/\delta_{\text{tot}} $，一般来说是尺度、所讨论的星系属性和红移的函数。数值模拟补充了分析结果，并显示星系更倾向于在不是太小（否则超新星反馈会阻碍坍缩）或太大（否则气体无法足够有效冷却）的晕中形成。

　　冷无碰撞暗物质的模拟产生了通常呈椭球形的暗物质晕，而不是球形。然而，非球形程度有限，并且在包括重子的模拟中发现更小。因此，在大多数现象学研究中采用的标准球形假设是相当合理的。

　　从数值数据计算出的单个晕的密度分布 $ \rho(r) $，在球对称近似中，倾向于遵循一个通用的斜率 $ s(r) \equiv d\ln\rho/d\ln r $，该斜率从内区的约 $-1$ 到外区的约 $-3$ 平滑变化。相比之下，由中的分析考虑建议的等温球体，具有 $s = -2$ 的斜率。模拟的结果可以被拟合为表 2.1 中的函数，如 'NFW'（来自 Navarro, Frenk, White；其斜率在半径 $r_s$ 处从 $-3$ 变化到 $-1$）或 'Einasto'（其斜率在 $r = r_s$ 时等于 $-2$，并持续演变）。个别引力束缚对象可以模拟到比它们的维里半径 $ r_{\text{vir}} $ 小大约 3 个数量级的尺寸（$ r_{\text{vir}} $ 定义为 $ \rho(r_{\text{vir}}) $ 比平均密度大 200 倍）。因此，模拟无法解析如果太小的潜在核心（其中密度 $ \rho $ 变为恒定）。粗略估计，对于像银河系这样的星系，与当前模拟兼容的具有大小约为 1 kpc 以下的核心的存在是可能的。

　　除了主要的晕结构外，模拟还揭示了在主晕内外和周围轨道上存在许多较小的子晕（见图 2.2）。它们的数量分布是 $ dn/dM \propto \sim 1/M^2 $，这意味着 $ M dn/d\ln M $ 大致与 M 无关。也就是说，对于任何给定的质量量级 $ M$，相似的总暗物质质量存储在对象中，从最大的形成结构到最小的解析结构，数量级约为 $ M \approx 10^5 M_\odot $。预计还存在模拟尚未解析的更小的晕。模拟显示，这些子晕具有更高的内部暗物质密度，并且平均来说，比同等质量的独立晕更集中。在 6.8.1 节中，我们将讨论子晕的存在如何增强暗物质湮灭的间接信号。模拟晕的其他特征似乎不那么通用。任何晕的浓度参数定义为 c = $ r_{\text{vir}}/r_{-2} $，其中 $ r_{-2} $ 是斜率达到 $s = -2 $ 的半径（在 Einasto 参数化中 $ r_{-2} = r_s $）。我们将讨论最小晕的质量，即微晕的质量：

　　对于弱尺度暗物质，可能与地球的质量相当，大约 $10^{-6} M_\odot$。微晕不是通过较小晕的合并形成的——专门的模拟表明，它们倾向于有 $c \approx 20 - 30$ 的浓度参数。浓度参数 $c$ 逐渐减小，对于更大的对象（星系和星系团），它们形成得更早，当时的宇宙密度较大，$c \approx$ 几。特别是，位于银河系晕内部的子晕具有更高的内部暗物质密度，并且平均来说，比同等质量的独立晕更集中。此外，子晕越靠近宿主晕的中心，它们就越集中。最后，球对称平均密度与平均径向速度的比值似乎遵循幂律，$\rho/v^3_r \propto 1/r^{1.875}$。

　　模拟有其固有的局限性：正常物质只是近似模拟，数值问题仍然存在，选择进行更详细计算的晕可能不是典型的，等等。将模拟与观测结果相比较，可能会发现一些差异：尖点-核心问题、多样性问题和缺失的卫星问题。

　　 N 体模拟的结果适用于银河系，只要它是一个典型的星系。由于我们不知道观测上银河系是否被一个非典型地具有高非球形性的晕所包围，我们将假设这不是这种情况，并使用一个平均球形暗物质晕来描述银河系。这可能是一个过度简化：测量到的银河系恒星速度表明它是通过两个大的前体星系相对较近的合并形成的，这可能使暗物质的局部分布复杂化。

1. ^ 这意味着无碰撞暗物质的坍缩不会形成黑洞。正常物质的情况截然不同。由于正常物质具有大的散射截面，对光子是不透明的，因此光子只能由紧凑物体的表面而不能由整个体积发射到周围环境。一个大型正常物质过密区域的坍缩倾向于分裂，形成许多恒星，而不是一个大物体。然后，恒星可以演化成恒星质量黑洞。超大质量黑洞是如何形成的是一个活跃的研究领域，有一种可能性是它们是通过吸积尘埃、气体以及恒星和恒星质量黑洞形成的。
2. ^ 更准确地说，我们实际上处理的是分布函数 $f(x, v, t)$，定义为 $f(x, v, t) d^3x d^3v$ 是在时间 $t$ 时在以 $x, v$ 为中心的 $d^3x d^3v$ 相空间体积中找到粒子的概率。对于一个球对称稳态系统，可以证明 $f$ 仅通过总能量（这是一个运动积分量）依赖于 $x, v$（$f$ 被称为是遍历的）。这就是为什么通过对所有速度积分 $f(\varepsilon)$ 可以得到暗物质粒子的空间分布，即它们的数量密度。将其乘以暗物质质量 $m$ 就得到了质量密度 $\rho$。

致读者：小时百科一直以来坚持所有内容免费无广告，这导致我们处于严重的亏损状态。长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。因此，我们请求广大读者热心打赏 ，使网站得以健康发展。如果看到这条信息的每位读者能慷慨打赏 20 元，我们一周就能脱离亏损，并在接下来的一年里向所有读者继续免费提供优质内容。但遗憾的是只有不到 1% 的读者愿意捐款，他们的付出帮助了 99% 的读者免费获取知识，我们在此表示感谢。