布拉伐格子、基元与原胞

                     

贡献者： Zona

　　 晶体最主要的特征是具有周期性重复的规则结果，可以看成是由不同原子组成的最小单元以某种方式在空间周期性重复平移的结果。这里有两个主要方面： 一是重复单元，二是重复排列的方式。只要确定了这两点，我们就可以得到整个晶体。

1. 布拉伐格子 基元

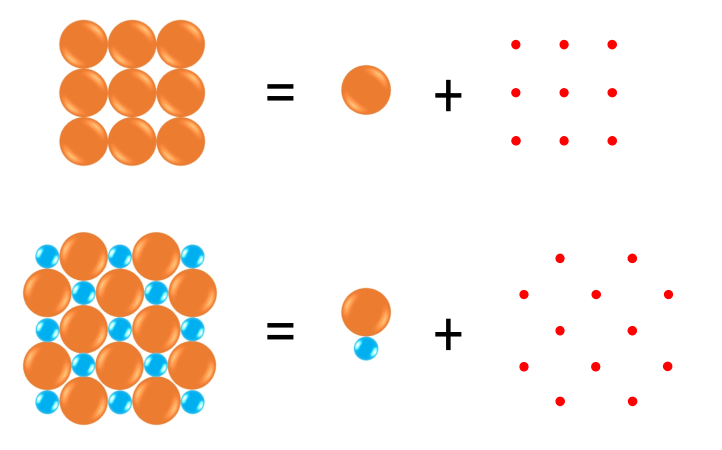
　　 早在 1866 年，布拉伐首先提出用晶格点阵来表示晶体中原子周期排列的方式，用基元表示最小重复单元。晶格点阵简称为晶格，又称为布拉伐格子。关于晶体、基元与晶格点阵的关系，我们可以这样理解：晶体 = 基元 + 晶格点阵。

　　 通过布拉伐格子与基元的简化，我们抓住了晶体结构中最主要的特征————即晶体中原子周期性的排列，体现了其所具有的平移对称性。注意，布拉伐格子是一个无限延展的理想点阵。因为严格来说，有限大小的晶格无法满足周期结构的平移对称性。因此，对于宏观晶体，我们引入周期性边界条件。同时，它忽略了实际晶体中的缺陷，如原子在其平衡位置的微小偏移等；不是真实的原子，是抽象的点，是基元所在的位置。

　　 打个比方，见过超市里的盒装鸡蛋吗？一个个鸡蛋整齐规律地垒在凹槽里，相当于一个个 “基元” 处在规律的 “布拉伐格子” 上。

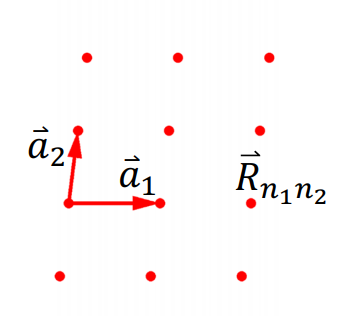
　　 注意，布拉伐格子具有平移前后晶格重叠和无限延展的特点。那么如何描述一个个基元的位置，即布拉伐格点的位置？回想描述空间的任意位置，我们总要确定一组基。在晶体中，这组基与布拉伐格子有关。引入格矢：

其中 $ \boldsymbol{\mathbf{a}} _1,~ \boldsymbol{\mathbf{a}} _2,~ \boldsymbol{\mathbf{a}} _3$ 是基矢，$a_1,~ a_2,~\ a_3$ 是晶格常数。$n_1, n_2, n_3$ 可以取任意整数，由此，我们可以得到整个布拉伐格子。

2. 原胞

　　 晶格的周期重复单元称为单胞或晶胞(unit cell)，体积（面积或长度）最小的周期重复单元称为原胞(primitive cell)。当我们将原胞或单胞平移所有可能的格矢时，将精确地填满整个空间，没有遗漏，也没有重复。

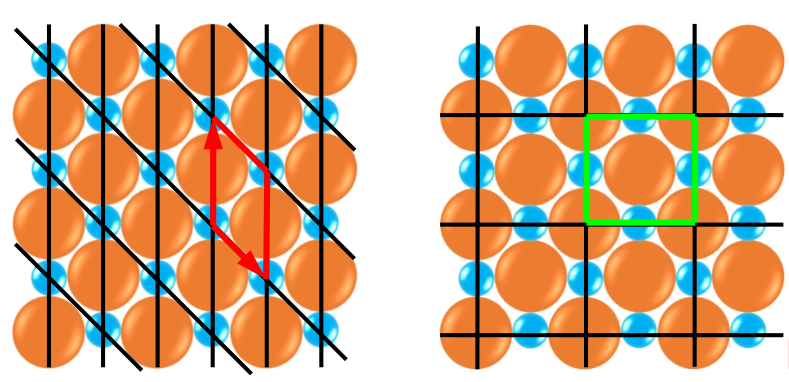
　　 原胞通常取由基矢构成的平行六面体（3d）或平行四边形（2d）。原胞的取法可以有多种，但它们的体积相同：

还有一种原胞的取法，以晶格中某一格点为中心，作其与近邻格点连线的垂直平分面（线），这些平面包围成的以该点为中心的最小体积是属于该点的Wigner-Seitz原胞，简称WS 原胞。

　　 初学者容易搞混原胞与基元的关系。注意，基元+晶格点阵=晶体，每一个布拉伐格点都代表一个基元；原胞则是从布拉伐点阵中取出的最小重复面积（体积），平移可以填满整个空间。下面有个图示可以帮助理解：

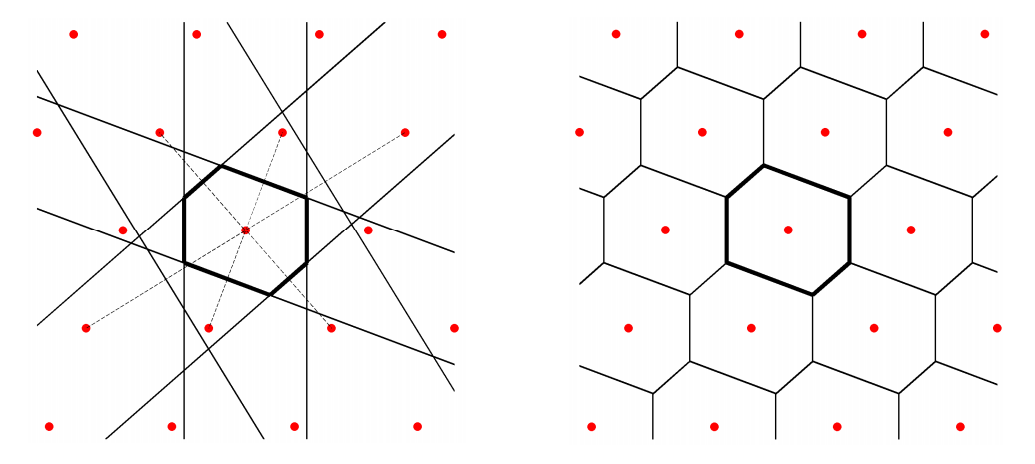
　　 图中，暗红色点的集合 ${R_{n_1,~ n_2}}$ 为布拉伐格子，黑色虚线圈出的是基元，两个红色箭头所标注的矢量 $ \boldsymbol{\mathbf{a}} _1,~ \boldsymbol{\mathbf{a}} _2$ 为基矢，暗红色阴影标注的格子为原胞，其面积最小。