八元数（综述）

                     

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章。

　　 在数学中，八元数是一种实数域上的赋范除代数，是一种超复数系统。八元数通常用大写字母 $\mathbf{O}$ 表示，也可以写作黑板粗体 $\mathbb{O}$。八元数具有 8 个维度，是四元数的 2 倍维数，而它们正是四元数的扩展。八元数是非交换的、非结合的，但满足一种较弱的结合性，即所谓的可交替性。此外，它们还具有幂结合性。

　　 八元数不像四元数和复数那样广为人知，后者在研究和应用上更为广泛。八元数与数学中的一些例外结构（exceptional structures，需要进一步澄清）有关，其中包括例外李群。八元数在弦理论、狭义相对论和量子逻辑等领域都有应用。将 Cayley–Dickson 构造应用于八元数，可以得到十六元数。

1. 历史

　　 八元数是在 1843 年 12 月由约翰·T·格雷夫斯发现的，他的灵感来自好友威廉·罗恩·哈密顿发现四元数。就在格雷夫斯发现八元数前不久，他在 1843 年 10 月 26 日写给哈密顿的一封信中写道：“如果凭借你的炼金术，你能炼出三磅黄金，为什么要止步于此呢？”\(^\text{[1]}\)

　　 格雷夫斯把他的发现称为 “octaves”（八度数），并在 1843 年 12 月 26 日写给哈密顿的信中提到这一点。\(^\text{[2]}\) 他最早发表研究结果的时间，比阿瑟·凯莱的文章稍晚一些。\(^\text{[3]}\) 八元数也被凯莱独立发现，有时被称为 Cayley 数或凯莱代数。\(^\text{[4]}\) 哈密顿后来描述过格雷夫斯发现八元数的早期经过。\(^\text{[5]}\)

2. 定义

　　 八元数可以被看作是实数的 八元组（octets 或 8-元组）。 每一个八元数都是单位八元数的实线性组合： $$ \{e_{0}, e_{1}, e_{2}, e_{3}, e_{4}, e_{5}, e_{6}, e_{7}\},~ $$ 其中，$e_{0}$ 是标量或实数元，可以与实数 1 对应。

　　 也就是说，每个八元数 $x$ 都可以写成以下形式： $$ x = x_{0} e_{0} + x_{1} e_{1} + x_{2} e_{2} + x_{3} e_{3} + x_{4} e_{4} + x_{5} e_{5} + x_{6} e_{6} + x_{7} e_{7},~ $$ 其中系数 $x_{i} \in \mathbb{R}$。

凯莱–迪克森构造

　　 一种更系统地定义八元数的方法是通过 凯莱–迪克森构造。将凯莱–迪克森构造应用于四元数，就能得到八元数。可以表示为 $\mathbb{O} = \mathcal{CD}(\mathbb{H}, 1)$.\(^\text{[6]}\)

　　 就像四元数可以定义为复数的有序对一样，八元数也可以定义为四元数的有序对。加法按分量逐一进行。若 $(a, b)$ 和 $(c, d)$ 是两对四元数，则它们的乘法定义为 $$ (a, b)(c, d) = (ac - d^{*}b,\; da + bc^{*}),~ $$ 其中 $z^{\*}$ 表示四元数 $z$ 的共轭。

　　 当将八个单位八元数与以下有序对对应时，这一定义与前面给出的等价： $$ (1, 0),\; (i, 0),\; (j, 0),\; (k, 0),\; (0, 1),\; (0, i),\; (0, j),\; (0, k).~ $$

3. 算术与运算

加法与减法

　　 八元数的加法与减法是逐项进行的，即对应项的系数相加或相减，这与四元数的情况相同。

乘法

　　 八元数的乘法要复杂得多。乘法对加法是分配的，因此两个八元数的积可以通过逐项相乘再求和得到，这一点和四元数类似。

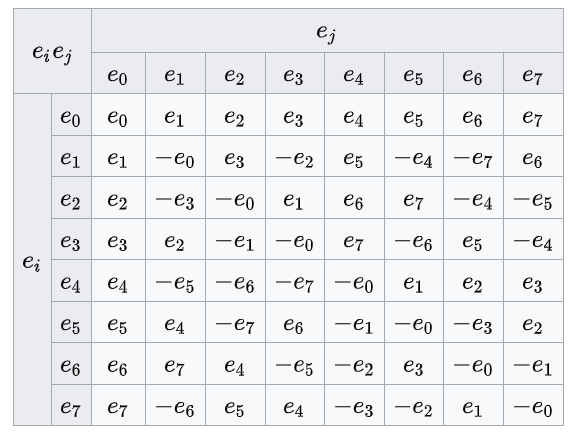
　　 每一对项的乘积由系数的乘法以及单位八元数的乘法表共同决定。一个这样的乘法表（由 阿瑟·凯莱（Arthur Cayley, 1845）和 约翰·T·格雷夫斯（John T. Graves, 1843）分别给出）如下所示：\(^\text{[7]}\)

图
图 1

　　 大多数乘法表的**非对角元素**都是**反对称的**，因此它几乎是一个**斜对称矩阵**（skew-symmetric matrix），只是主对角线元素，以及 $e\_{0}$ 所在的行和列例外。

　　 这个乘法表可以总结为如下形式：[8] $$ e_{\ell} e_{m} = \begin{cases} e_{m}, & \text{if } \ell = 0, \\ e_{\ell}, & \text{if } m = 0, \\ -\delta_{\ell m} e_{0} + \varepsilon_{\ell mn} e_{n}, & \text{otherwise}, \end{cases}~ $$ 其中：$\delta_{\ell m}$ 是 Kronecker delta（当 $\ell = m$ 时等于 1，当 $\ell \neq m$ 时等于 0）；$\varepsilon_{\ell mn}$ 是一个完全反对称张量：当 $(\ell m n)$ 等于下列之一时，取值为 $+1$：$(123),\; (145),\; (176),\; (246),\; (257),\; (347),\; (365),$ 以及这些三元组的偶数次排列；对于这些三元组的奇数次排列，则取值为 $-1$。例如：$\varepsilon_{123} = +1, \quad \varepsilon_{132} = \varepsilon_{213} = -1, \quad\varepsilon_{312} = \varepsilon_{231} = +1$ 若三个指标中有任意两个相同，则 $\varepsilon_{\ell mn} = 0$。

　　 然而，上述定义并不是唯一的。事实上，这只是 480 种可能的八元数乘法定义之一（其中 $e_{0} = 1$）。其他定义可以通过对非标量基元素 ${ e\_{1}, e_{2}, e_{3}, e_{4}, e_{5}, e_{6}, e_{7} }$ 进行置换和符号变换得到。所有这 $480$ 种代数都是同构的，因此通常没有必要区分具体采用哪一种乘法规则。

图
图 2

　　 有时会采用一种变体，即将基底元素标记为射影线上 ${\infty, 0, 1, 2, \ldots, 6}$，该射影线是定义在有限域 $\mathrm{GF}(7)$ 上的。此时，乘法规则为 $e_{\infty} = 1, \quad e_{0} e_{1} = e_{3}$，以及所有通过给下标加上常数（模 7）得到的方程。换句话说，利用以下七个三元组：$(0,1,3), \; (1,2,4), \; (2,3,5), \; (3,4,6), \; (4,5,0), \; (5,6,1), \; (6,0,2)$.这些正是**长度为 7 的二次剩余码在 $\mathrm{GF}(2)$ 上的非零码字。在这里存在两个对称性：一个是阶为 7 的对称性，即对所有下标加上模 7 的常数；另一个是阶为 3 的对称性，即将所有下标乘以模 7 的一个二次剩余（1,2,4）。这七个三元组也可以看作是集合 {1,2,4} 的七个平移，它们形成有限域 $\mathrm{GF}(7)$（含七个元素）上的一个循环 (7,3,1) 差集。

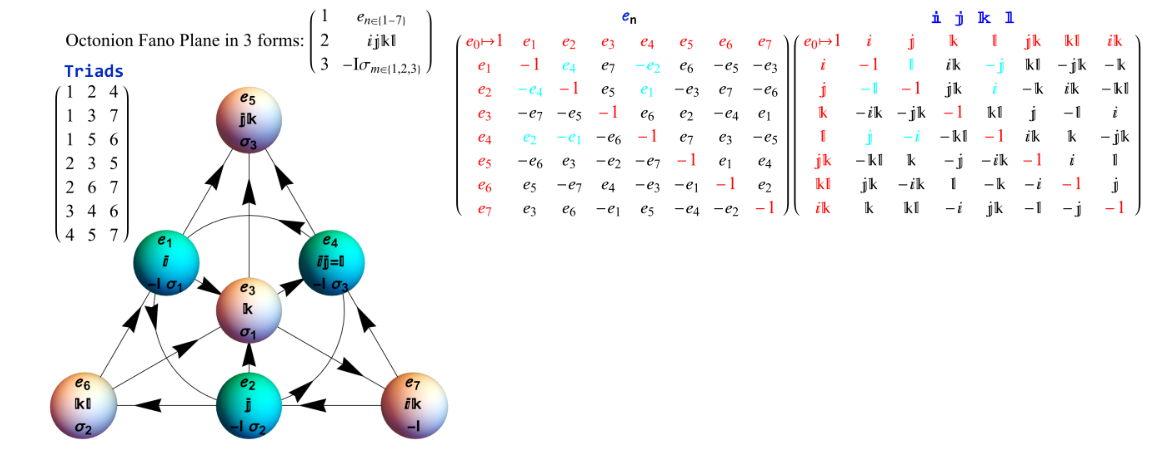
　　 前文所示的法诺平面，配合 $e\_{n}$ 和 IJKL 乘法矩阵，也包含了一个符号为 $(-,-,-,-)$ 的几何代数基。它由以下七个四元数型三元组给出（省略了标量单位元）： $$ (I, j, k), \; (i, J, k), \; (i, j, K), \; (I, J, K), \; (\star I, i, l), \; (\star J, j, l), \; (\star K, k, l),~ $$ 或者等价地写作： $$ (\sigma_{1}, j, k), \; (i, \sigma_{2}, k), \; (i, j, \sigma_{3}), \; (\sigma_{1}, \sigma_{2}, \sigma_{3}), \; (\star \sigma_{1}, i, l), \; (\star \sigma_{2}, j, l), \; (\star \sigma_{3}, k, l).~ $$ 其中：小写符号 ${i, j, k, l}$ 表示向量，例如 ${\gamma_{0}, \gamma_{1}, \gamma_{2}, \gamma_{3}}$ 大写符号 ${I, J, K} = {\sigma_{1}, \sigma_{2}, \sigma_{3}}$ 表示双向量，例如 $\gamma_{{1,2,3}} \gamma_{0},$ 算子 $\star = i j k l$ 是伪标量元。

　　 如果强制 $\star$ 等于单位元，那么乘法将不再是结合的，但此时可以将 $\star$ 从乘法表中移除，从而得到一个八元数的乘法表。若保持 $\star = i j k l$ 作为结合的运算元（因此不将四维几何代数约化为八元数代数），则整个乘法表都可以由 $\star$ 的定义导出。考虑上文给出的 $\gamma$ 矩阵，第五个 $\gamma$ 矩阵的定义式：$\gamma_{5}$, 正表明它是一个由 $\gamma$ 矩阵形成的四维几何代数的 $\star$ 运算结果。

法诺平面助记法

图
图 3：单位八元数乘积的助记法 \(^\text{[11]}\)

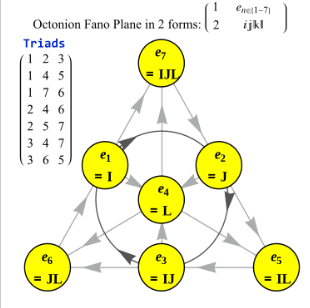
　　 一种记忆单位八元数乘法的便利助记法是通过图示来完成的，这个图表示了凯莱和格雷夫斯给出的乘法表。\(^\text{[7][12]}\) 该图由 7 个点和 7 条线组成（其中通过点 1,2,3 的圆也被视为一条线），被称为法诺平面。这些线具有方向性。这 7 个点对应于 $\operatorname{\mathcal{I_{m}}}!\bigl[\mathbb{O}\bigr]$ 的 7 个标准基元素（见下文定义）。任意两个不同的点恰好确定一条唯一的线，每条线也恰好穿过 3 个点。

　　 设 $(a, b, c)$ 是位于某条线上且按箭头方向排序的三元组，则乘法规则为： $$ ab = c, \quad ba = -c,~ $$ 并结合循环置换。

　　 此外，还需满足以下规则：

　　 这些规则共同完全确定了八元数的乘法结构。此外，法诺平面中的每一条线都生成了一个与四元数 $\mathbf{H}$ 同构的子代数。

共轭、范数与逆元

图
图 4：一种三维助记可视化方法，将前述八元数示例中的实数顶点 $e_{0}$ 作为公共顶点，展示 7 个三元组对应的超平面 \(^\text{[11]}\)

　　 一个八元数 $$ x = x_{0} e_{0} + x_{1} e_{1} + x_{2} e_{2} + x_{3} e_{3} + x_{4} e_{4} + x_{5} e_{5} + x_{6} e_{6} + x_{7} e_{7}~ $$ 的共轭定义为 $$ x^{*} = x_{0} e_{0} - x_{1} e_{1} - x_{2} e_{2} - x_{3} e_{3} - x_{4} e_{4} - x_{5} e_{5} - x_{6} e_{6} - x_{7} e_{7}.~ $$ 共轭运算是 $\mathbb{O}$ 上的一个自反，并满足 $(xy)^{*} = y^{*} x^{*} \quad \text{（注意次序变化）}$.

　　 八元数 $x$ 的实部为 $$ \frac{x + x^{*}}{2} = x_{0} e_{0},~ $$ 虚部（纯部）为 $$ \frac{x - x^{*}}{2} = x_{1} e_{1} + x_{2} e_{2} + x_{3} e_{3} + x_{4} e_{4} + x_{5} e_{5} + x_{6} e_{6} + x_{7} e_{7}.~ $$ 所有纯虚八元数组成 $\mathbb{O}$ 的一个 7 维子空间，记作 $\operatorname{\mathcal{I_{m}}}\!\bigl[\mathbb{O}\bigr]$.

　　 八元数的共轭还满足以下关系： $$ -6x^{*} = x + (e_{1}x)e_{1} + (e_{2}x)e_{2} + (e_{3}x)e_{3} + (e_{4}x)e_{4} + (e_{5}x)e_{5} + (e_{6}x)e_{6} + (e_{7}x)e_{7}.~ $$

　　 八元数与其共轭的乘积总是非负实数： $$ x^{*}x = x_{0}^{2} + x_{1}^{2} + x_{2}^{2} + x_{3}^{2} + x_{4}^{2} + x_{5}^{2} + x_{6}^{2} + x_{7}^{2}.~ $$ 因此，可以定义八元数的范数为 $$ \|x\| = \sqrt{x^{*}x}.~ $$ 这个范数与 $\mathbb{R}^{8}$ 上的标准 8 维欧几里得范数一致。

　　 由于 $\mathbb{O}$ 上存在范数，所以每个非零元素都有逆元。对 $x \neq 0$，其唯一的逆元 $x^{-1}$（满足 $xx^{-1} = x^{-1}x = 1$）为 $$ x^{-1} = \frac{x^{*}}{\|x\|^{2}}.~ $$

指数与极坐标形式

　　 任意一个八元数 $x$ 都可以分解为其实部和虚部： $$ x = \mathfrak{R}(x) + \mathfrak{I}(x),~ $$ 其中，实部 $\mathfrak{R}(x)$ 有时也称为标量部分，虚部 $\mathfrak{I}(x)$ 称为向量部分。

　　 我们定义与 $x$ 对应的单位向量 $u$ 为： $$ u = \frac{\mathfrak{I}(x)}{\|\mathfrak{I}(x)\|}.~ $$ 它是一个范数为 1 的纯八元数。

　　 可以证明 \(^\text{[13]}\)，任何非零八元数都可以写成： $$ o = \|o\|\bigl(\cos \theta + u \sin \theta \bigr) = \|o\| e^{u\theta},~ $$ 从而给出了八元数的极坐标形式。

4. 性质

　　 八元数乘法既不是交换的： $$ e_{i} e_{j} = - e_{j} e_{i} \neq e_{j} e_{i}, \quad \text{当 } i, j \text{ 不同且非零时},~ $$ 也不是结合的： $$ (e_{i} e_{j}) e_{k} = - e_{i} (e_{j} e_{k}) \neq e_{i}(e_{j} e_{k}), \quad \text{当 } i, j, k \text{ 不同且非零且 } e_{i} e_{j} \neq \pm e_{k} \text{时}.~ $$ 不过，八元数满足一种较弱的结合性：它们是可交替的。这意味着由任意两个元素生成的子代数是结合的。实际上，可以证明由 $\mathbb{O}$ 中任意两个元素生成的子代数同构于 $\mathbb{R}$、$\mathbb{C}$ 或 $\mathbb{H}$，而这些代数都是结合代数。由于不具结合性，八元数不能像实数、复数、四元数那样表示为实数矩阵环的子代数。

　　 八元数保留了 $\mathbb{R}$、$\mathbb{C}$ 和 $\mathbb{H}$ 的一个重要性质：其范数满足 $$ \|xy\| = \|x\|\ \|y\|.~ $$ 这说明八元数构成一个组成代数。由凯莱–迪克森构造继续扩展得到的更高维代数（例如十六元数 sedenions）都不再满足这一性质，它们存在零因子。更广泛的数系也存在，其中一些数系具有乘法模（例如 16 维的圆锥十六元数 conic sedenions）。不过，这些数系的模与范数的定义不同，并且它们同样包含零因子。

　　 赫尔维茨证明了：在实数域上，$\mathbb{R}$、$\mathbb{C}$、$\mathbb{H}$ 和 $\mathbb{O}$ 是唯一的赋范除代数。这四个代数也是实数域上唯一的有限维可交替除代数（在同构意义下）。

　　 由于八元数不具结合性，$\mathbb{O}$ 的非零元素不构成群。但它们却构成一个环路，更确切地说是一个 Moufang 环路。

对易子与叉积

　　 两个八元数 $x$ 和 $y$ 的对易子定义为 $$ [x,y] = xy - yx.~ $$ 它是反对称的，并且是一个虚八元数。如果只在虚子空间 $\operatorname{\mathcal{I_{m}}}\!\bigl[\mathbb{O}\bigr]$ 上考虑这一运算，就得到该空间上的一个乘法，即七维叉积，其定义为 $$ x \times y = \tfrac{1}{2}(xy - yx).~ $$ 与三维叉积类似，它给出的结果是一个同时正交于 $x$ 和 $y$ 的向量，其模长为 $$ \|x \times y\| = \|x\| \ \|y\| \ \sin \theta.~ $$ 但与三维情况不同的是，这个叉积并不是唯一确定的。实际上存在多种不同的叉积形式，每一种都依赖于所选取的八元数乘法。\(^\text{[14]}\)

自同构

　　 八元数的一个自同构 $A$ 是 $\mathbb{O}$ 上的一个可逆线性变换，它满足 $$ A(xy) = A(x) \ A(y).~ $$ 所有八元数自同构的集合构成一个群，称为 $G\_{2}$ 群。\(^\text{[15]}\)$G\_{2}$ 是一个单连通、紧致、实李群，维度为 14。它是例外李群中最小的一个，并同构于 $\operatorname{Spin}(7)$ 的一个子群——该子群保持其 8 维实旋量表示中的任意一个特定向量不变。而 $\operatorname{Spin}(7)$ 本身又是下面将要描述的等变群的一个子群。

　　 另见：$\operatorname{PSL}(2,7)$ ——法诺平面的自同构群。

同构变换

　　 一个代数的同构变换是一个三元组 $(a,b,c)$，其中 $a,b,c$ 都是双射线性映射，并且若 $ xy = z$，则有 $a(x)b(y) = c(z)$。当 $a=b=c$ 时，这就是一个自同构。代数的同构群是所有同构变换构成的群，它包含自同构群作为子群。

　　 八元数的同构群是 $\operatorname{Spin}\_{8}(\mathbb{R})$，其中 $a,b,c$ 分别对应其三个 8 维表示。\(^\text{[16]}\) 当 $c$ 固定单位元时，对应的子群是 $\operatorname{Spin}\_{7}(\mathbb{R})$；当 $a,b,c$ 都固定单位元时，对应的子群就是自同构群 $G\_{2}$。

矩阵表示

　　 就像四元数可以用矩阵表示一样，八元数也可以用四元数矩阵表来表示。具体而言，由于任意一个八元数都可以表示为一对四元数 $(q\_{0}, q\_{1})$，我们将其表示为 $$ (q_{0},q_{1}) \;\longmapsto\; \begin{bmatrix} q_{0} & q_{1} \\ - q_{1}^{*} & q_{0}^{*} \end{bmatrix}.~ $$ 这里 $q\_{i}^{\*}$ 表示四元数的共轭。

　　 在使用一种稍加修改的（非结合的）四元数矩阵乘法时： $$ \begin{bmatrix} \alpha_{0} & \alpha_{1} \\ \alpha_{2} & \alpha_{3} \end{bmatrix} \circ \begin{bmatrix} \beta_{0} & \beta_{1} \\ \beta_{2} & \beta_{3} \end{bmatrix} = \begin{bmatrix} \alpha_{0}\beta_{0}+\beta_{2}\alpha_{1} & \beta_{1}\alpha_{0}+\alpha_{1}\beta_{3} \\ \beta_{0}\alpha_{2}+\alpha_{3}\beta_{2} & \alpha_{2}\beta_{1}+\alpha_{3}\beta_{3} \end{bmatrix},~ $$ 我们就可以将八元数的加法和乘法转化为对应的四元数矩阵运算。\(^\text{[6]}\)

5. 应用

　　 八元数在其他数学结构的分类与构造中扮演了重要角色。例如：例外李群 $G_{2}$ 是八元数的自同构群；其他例外李群 $F_{4}$、$E_{6}$、$E_{7}$ 和 $E_{8}$ 可以理解为利用八元数定义的某些射影平面的等距变换群。\(^\text{[17]}\) 由 $3\times 3$ 自伴八元数矩阵构成的集合，配合对称化的矩阵乘法，定义了 Albert 代数。在离散数学中，八元数提供了 Leech 晶格的一种初等推导方法，因此与散在单群密切相关。\(^\text{[[18][19]]}\)

　　 八元数在物理学中的应用大多仍停留在猜想阶段。例如：在 1970 年代，人们曾尝试利用八元数 Hilbert 空间来理解夸克。\(^\text{[20]}\) 已知八元数（以及 “只有四种赋范除代数存在” 这一事实）与可构造超对称量子场论的时空维数相关。\(^\text{[[21][22]]}\) 也有学者尝试通过八元数构造来得到标准模型，例如使用所谓的 Dixon 代数 $\mathbb{C} \otimes \mathbb{H} \otimes \mathbb{O}$.\(^\text{[23][24]}\)

　　 八元数出现在黑洞熵、量子信息科学 \(^\text{[25][26]}\)、弦理论 \(^\text{[27]}\) 和图像处理 \(^\text{[28]}\) 的研究中。

　　 在机器人学中，八元数被用于手眼标定问题的解法。\(^\text{[29]}\)

　　 在机器学习中，深度八元数网络为高效而紧凑的表达提供了一种方式。\(^\text{[30][31]}\)

6. 整数八元数

　　 定义整数八元数有几种自然方式。最简单的方法是取坐标均为整数的八元数。这给出了一个定义在整数环上的非结合代数，称为 Graves 八元数。然而，它并不是环论意义下的极大整阶；事实上，恰好存在 7 个包含它的极大整阶。这七个极大整阶在自同构下都是等价的。通常所说的 “整数八元数” 指的是这七个极大整阶中的一个固定选择。

　　 这些极大整阶最早由 Kirmse (1924)、Dickson 和 Bruck 构造。具体做法如下：将八个基向量标记为域 $\mathrm{GF}(7)$ 上射影直线的点。首先构造所谓的 Kirmse 整数：它们是坐标为整数或半整数的八元数，并且在下面给出的 16 个集合之一上取半整数（即奇数的一半）： $$ \varnothing,\; (\infty124),\; (\infty235),\; (\infty346),\; (\infty450),\; (\infty561),\; (\infty602),\; (\infty013),\; (\infty0123456),\; (0356),\; (1460),\; (2501),\; (3612),\; (4023),\; (5134),\; (6245),~ $$ 这些集合来自长度为 8 的扩展二次剩余码，定义在 $\mathrm{GF}(2)$ 上：即 $\varnothing$、$(\infty124)$ 及其在模 7 加常数下的像，以及这 8 个集合的补集。接着，将 $\infty$ 与任意一个其他坐标交换；这个操作会将 Kirmse 整数双射到另一个集合上，而这个集合正是一个极大整阶。共有 7 种方式可以进行这种交换，得到 7 个极大整阶，它们在 $0123456$ 的循环置换下互为等价。（Kirmse 曾错误地声称 Kirmse 整数本身也是一个极大整阶，因此他认为有 8 个极大整阶。但正如 Coxeter (1946) 指出的，它们在乘法下并不封闭；这一错误在一些文献中仍然出现。）

　　 Kirmse 整数与这 7 个极大整阶都是与 $E_{8}$ 晶格等距的，只是整体缩放了一个因子 $1/\sqrt{2}$。特别地，在每一个极大整阶中都有 240 个非零最小范数为 1 的元素，它们构成一个阶为 240 的 Moufang 环路。

　　 整数八元数具有 “带余除法” 的性质：对于给定的整数八元数 $a$ 和 $b \neq 0$，存在 $q,r$ 使得 $a = qb + r$，且余数 $r$ 的范数小于 $b$ 的范数。在整数八元数中，所有的左理想与右理想都是双边理想，而唯一的双边理想是形如 $n\mathbf{O}$ 的主理想，其中 $n$ 是非负整数。

　　 整数八元数存在某种形式的素因子分解，但由于八元数不结合，积的结果依赖于乘法顺序，因此表述并不直接。不可约整数八元数正是那些范数为素数的八元数，并且每个整数八元数都可以写作不可约八元数的乘积。更精确地说，若一个整数八元数的范数为 $mn$，则它可以分解为范数分别为 $m$ 和 $n$ 的整数八元数的积。

　　 整数八元数的自同构群是 $G\_{2}(\mathbf{F}_{2})$，其阶为 $12,096$。该群包含一个指数为 2 的单群子群，它同构于酉群 $^{2}A_{2}(3^{2})$。整数八元数的同构群是 $E\_{8}$ 晶格旋转群的完美双覆盖。

7. 参见

8. 注释

  1. （Baez 2002, p. 1）
  2. Sabadini, Irene; Shapiro, Michael; Sommen, Franciscus (2009-04-21)，《超复分析》（*Hypercomplex Analysis*），Springer Science & Business Media，ISBN 978-3-7643-9893-4
  3. （Graves 1845）
  4. Cayley, Arthur (1845), “On Jacobi's Elliptic functions, in reply to the Rev. Brice Bronwin; and on Quaternions”，Philosophical Magazine，26 (172): 208–211，doi:10.1080/14786444508645107。附录重印于 The Collected Mathematical Papers，Johnson Reprint Co., New York, 1963, p. 127
  5. Hamilton (1848), “Note, by Sir W. R. Hamilton, respecting the researches of John T. Graves, Esq.”，Transactions of the Royal Irish Academy*，21: 338–341
  6. “Ensembles de nombre” (PDF)（法语），Forum Futura-Science，2011 年 9 月 6 日，2024 年 10 月 11 日检索
  7. Gentili, G.; Stoppato, C.; Struppa, D.C.; Vlacci, F. (2009), “Recent developments for regular functions of a hypercomplex variable”，载于 Sabadini, I.; Shapiro, M.; Sommen, F. (编)，《超复分析》，Birkhäuser，p. 168，ISBN 978-3-7643-9892-7 —— via Google Books
  8. Sabinin, L.V.; Sbitneva, L.; Shestakov, I.P. (2006), “§17.2 八元数代数及其正则双模表示”，《非结合代数及其应用》，Boca Raton, FL: CRC Press，p. 235，ISBN 0-8247-2669-3 —— via Google Books
  9. Abłamowicz, Rafał; Lounesto, Pertti; Parra, Josep M. (1996), “§ 四种八元数基编号”，《含数值与符号计算的克利福德代数》，Birkhäuser，p. 202，ISBN 0-8176-3907-1 —— via Google Books
  10. Schray, Jörg; Manogue, Corinne A. (1996 年 1 月), “八元数的克利福德代数表示与三重性”，Foundations of Physics，26 (1): 17–70，arXiv\:hep-th/9407179，Bibcode:1996FoPh...26...17S，doi:10.1007/BF02058887，S2CID 119604596
    可获取版本：Schray, Jörg; Manogue, Corinne A. (1996), “Octonionic representations of Clifford algebras and triality”，Foundations of Physics，26 (1): 17–70，arXiv\:hep-th/9407179，Bibcode:1996FoPh...26...17S，doi:10.1007/BF02058887，特别见图 1 (.png)，arXiv（图像）
  11. （Baez 2002, p. 6）
  12. Dray, Tevian & Manogue, Corinne A. (2004), “第 29 章：用八元数描述基本粒子”，载于 Abłamowicz, Rafał (编)，《克利福德代数：在数学、物理与工程中的应用》，Birkhäuser，图 29.1：射影平面上的乘法表表示，p. 452，ISBN 0-8176-3525-4 —— via Google Books
  13. “Ensembles de nombres”（法语 PDF），Forum Futura-Science，2011 年 9 月 6 日，2025 年 2 月 24 日检索
  14. Baez (2002), pp. 37–38
  15. （Conway & Smith 2003, ch. 8.6）
  16. （Conway & Smith 2003, ch. 8）
  17. Baez (2002), 第 4 节
  18. Wilson, Robert A. (2009-09-15), “八元数与 Leech 晶格”，Journal of Algebra，322 (6): 2186–2190，doi:10.1016/j.jalgebra.2009.03.021
  19. Wilson, Robert A. (2010-08-13), “康威群与八元数”，Journal of Group Theory，14: 1–8，doi:10.1515/jgt.2010.038，S2CID 16590883
  20. Günaydin, M.; Gürsey, F. (1973), “夸克结构与八元数”，Journal of Mathematical Physics，14 (11): 1651–1667，Bibcode:1973JMP....14.1651G，doi:10.1063/1.1666240
    Günaydin, M.; Gürsey, F. (1974), “夸克统计与八元数”，Physical Review D，9 (12): 3387–3391，Bibcode:1974PhRvD...9.3387G，doi:10.1103/PhysRevD.9.3387
  21. Kugo, Taichiro; Townsend, Paul (1983-07-11)，《超对称与除代数》，Nuclear Physics B，221 (2): 357–380，Bibcode:1983NuPhB.221..357K，doi:10.1016/0550-3213(83)90584-9
  22. Baez, John C.; Huerta, John (2010)，《除代数与超对称 I》，见 Doran, R.; Friedman, G.; Rosenberg, J. (编)，Superstrings, Geometry, Topology, and C*-algebras\，American Mathematical Society，arXiv:0909.0551
  23. Wolchover, Natalie (2018-07-20)，《可能潜藏在自然法则之下的奇特数学》，Quanta Magazine，2018-10-30 检索 Furey, Cohl (2012-07-20)，《理想的统一理论》，*Physical Review D*，86 (2): 025024，arXiv:1002.1497，Bibcode:2012PhRvD..86b5024F，doi:10.1103/PhysRevD.86.025024，S2CID 118458623
  24. Furey, Cohl (2018-10-10)，《三代、两个未破缺的规范对称性和一个八维代数》），Physics Letters B，785: 84–89，arXiv:1910.08395，Bibcode:2018PhLB..785...84F，doi:10.1016/j.physletb.2018.08.032，S2CID 126205768
    Stoica, O.C. (2018)，《来自复克利福德代数 $\mathbb{C}\ell_{6}$ 的轻子、夸克与规范》（*Leptons, quarks, and gauge from the complex Clifford algebra $\mathbb{C}\ell_{6}$*），*Advances in Applied Clifford Algebras*，28: 52，arXiv:1702.04336，doi:10.1007/s00006-018-0869-4，S2CID 125913482
    Gresnigt, Niels G. (2017-11-21)，《量子群与辫群作为基本对称性》，European Physical Society conference on High Energy Physics，2017 年 7 月 5–12 日，意大利威尼斯，arXiv:1711.09011
    Dixon, Geoffrey M. (1994)，《除代数：八元数、四元数、复数与物理的代数设计》，Springer-Verlag，doi:10.1007/978-1-4757-2315-1，ISBN978-0-7923-2890-2，OCLC 30399883Baez, John C. (2011-01-29)，《三重方式（第 4 部分）》，The n-Category Café，2018-11-02 检索
  25. Borsten, Leron; Dahanayake, Duminda; Duff, Michael J.; Ebrahim, Hajar; Rubens, Williams (2009)，《黑洞、量子比特与八元数》，Physics Reports，471 (3–4): 113–219，arXiv:0809.4685，Bibcode:2009PhR...471..113B，doi:10.1016/j.physrep.2008.11.002，S2CID 118488578
  26. Stacey, Blake C. (2017)，《散在 SIC 与赋范除代数》，Foundations of Physics，47 (8): 1060–1064，arXiv:1605.01426，Bibcode:2017FoPh...47.1060S，doi:10.1007/s10701-017-0087-2，S2CID 118438232
  27. 《超越时空：8D —— 冲浪者的乐园》，New Scientist
  28. Jacome, Roman; Mishra, Kumar Vijay; Sadler, Brian M.; Arguello, Henry (2024)，《八元数相位恢复》，IEEE Signal Processing Letters，31: 1615，arXiv:2308.15784，Bibcode:2024ISPL...31.1615J，doi:10.1109/LSP.2024.3411934
  29. Wu, J.; Sun, Y.; Wang, M.; Liu, M. (2020 年 6 月)，《手眼标定：一种基于四维 Procrustes 分析的方法》，IEEE Transactions on Instrumentation and Measurement，69 (6): 2966–2981，Bibcode:2020ITIM...69.2966W，doi:10.1109/TIM.2019.2930710，S2CID 201245901
  30. Wu, J.; Xu, L.; Wu, F.; Kong, Y.; Senhadji, L.; Shu, H. (2020)，《深度八元数网络》，Neurocomputing，397: 179–191，doi:10.1016/j.neucom.2020.02.053，S2CID 84186686，hal-02865295
  31. Bojesomo, Alabi; Liatsis, Panos; Almarzouqi, Hasan (2023)，《基于参数高效八元数架构的海洋垃圾分割》，IEEE Geoscience and Remote Sensing Letters，20: 1–5，Bibcode:2023IGRSL..2021177B，doi:10.1109/lgrs.2023.3321177

9. 参考文献

10. 外部链接


致读者： 小时百科一直以来坚持所有内容免费无广告，这导致我们处于严重的亏损状态。 长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。 因此，我们请求广大读者热心打赏 ，使网站得以健康发展。 如果看到这条信息的每位读者能慷慨打赏 20 元，我们一周就能脱离亏损， 并在接下来的一年里向所有读者继续免费提供优质内容。 但遗憾的是只有不到 1% 的读者愿意捐款， 他们的付出帮助了 99% 的读者免费获取知识， 我们在此表示感谢。

                     

友情链接： 超理论坛　|　©小时科技 保留一切权利