布尔代数（综述）

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章。

　　 在抽象代数中，布尔代数或布尔格是一个带补的分配格。这种代数结构刻画了集合运算和逻辑运算的基本性质。布尔代数可以被看作是幂集代数或集合域的推广，或者其元素可以被看作是广义真值。它也是德摩根代数和克莱尼代数的一个特殊情形。

　　 每一个布尔代数都可以产生一个布尔环，反之亦然，其中环的乘法对应于合取或交运算∧，环的加法对应于异或或对称差（不是析取 ∨）。然而，布尔环理论在两个运算之间本质上是不对称的，而布尔代数的公理和定理则通过对偶性原理体现出理论的对称性。\(^\text{[1]}\)

1. 历史

　　 “布尔代数” 一词是为了纪念自学成才的英国数学家乔治·布尔而命名的。他最初在 1847 年出版的一本小册子《逻辑的数学分析》中引入了这种代数系统，该书是为回应奥古斯都·德·摩根与威廉·汉密尔顿之间一场持续的公共争论而写的。随后，他在 1854 年出版了更为重要的著作 《思维定律》。布尔的表述在一些重要方面与上文所描述的有所不同。例如，在布尔的体系中，合取和析取并不是一对对偶运算。布尔代数在 1860 年代逐渐成形，出现在威廉·杰文斯和查尔斯·桑德斯·皮尔斯撰写的论文中。布尔代数和分配格的首次系统化呈现归功于恩斯特·施罗德 1890 年的 《讲义》。布尔代数在英语中的第一次大规模研究则是 A. N. 怀特海 1898 年的 《普遍代数》。布尔代数作为一种现代公理化意义上的公理化代数结构始于爱德华·V·亨廷顿 1904 年的一篇论文。布尔代数真正成为严肃数学的一部分是在 1930 年代马歇尔·斯通的工作中，以及 1940 年加勒特·伯科夫的 《格论》 中。在 1960 年代，保罗·科恩、达纳·斯科特等人使用布尔代数的衍生理论——强迫法和布尔值模型——在数理逻辑和公理化集合论中发现了深刻的新成果。

2. 定义

　　 一个布尔代数是一个集合 $A$，配备如下结构：两个二元运算：$\land$（称为 “交” 或 “与”，meet / and）$\lor$（称为 “并” 或 “或”，join / or）一个一元运算：$\lnot$（称为 “补” 或 “非”，complement / not）两个特殊元素：$0$ 和 $1$（称为 “底元” 和 “顶元”，或 “最小元” 和 “最大元”，也分别记作 $\bot$ 和 $\top$）使得对所有 $A$ 中的元素 $a, b, c$，以下公理成立：\(^\text{[2]}\)
结合律： $$ a \lor (b \lor c) = (a \lor b) \lor c, \quad a \land (b \land c) = (a \land b) \land c~ $$ 交换律： $$ a \lor b = b \lor a, \quad a \land b = b \land a~ $$ 吸收律： $$ a \lor (a \land b) = a, \quad a \land (a \lor b) = a~ $$ 幺元 $$ a \lor 0 = a, \quad a \land 1 = a~ $$ 分配律： $$ a \lor (b \land c) = (a \lor b) \land (a \lor c), \quad a \land (b \lor c) = (a \land b) \lor (a \land c)~ $$ 补元： $$ a \lor \lnot a = 1, \quad a \land \lnot a = 0~ $$ 注意：吸收律甚至结合律可以从其他公理推导出来，因此可以从公理集合中省略（参见 “已证性质” 部分）。

　　 一个只有一个元素的布尔代数称为平凡布尔代数或退化布尔代数。（在较早的著作中，一些作者要求 0 和 1 必须是不同的元素，以排除这种情况。）

　　 由上面最后三对公理（恒等律、分配律和补元律），或由吸收律可以推出： $$ a = b \land a \quad \text{当且仅当} \quad a \lor b = b~ $$ 定义关系 $a \le b$ 当且仅当上述等价条件成立，则该关系是一个偏序关系，具有最小元 0 和最大元 1。两个元素的交 $a \land b$ 和并 $a \lor b$ 分别与它们关于 $\le$ 的下确界和上确界一致。

　　 前四对公理构成了有界格的定义。

　　 由前五对公理可以推出，任何补元都是唯一的。

　　 这组公理是自对偶的，即如果在某个公理中交换 $\lor$ 与 $\land$，并交换 0 与 1，得到的仍然是一个公理。因此，通过对一个布尔代数（或布尔格）应用这一操作，可以得到另一个具有相同元素的布尔代数，这个代数称为它的对偶。\(^\text{[3]}\)

3. 例子

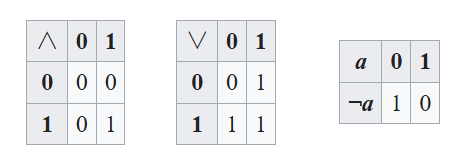
• 最简单的非平凡布尔代数是二元布尔代数，它只有两个元素 0 和 1，并且由以下规则定义：
  
  图 2
• 它在逻辑学中有广泛应用，将 0 解释为 “假”，1 解释为 “真”，∧ 表示 “与 (and)”，∨ 表示 “或 (or)”，¬ 表示 “非 (not)”。包含变量和布尔运算的表达式代表命题形式，当且仅当相应的命题形式在逻辑上等价时，可以使用上述公理证明两个这样的表达式相等。
• 二元布尔代数还用于电气工程中的电路设计；\(^\text{[note 1]}\) 在这里，0 和 1 表示数字电路中一位 (bit) 的两种不同状态，通常是高电平和低电平。电路通过包含变量的表达式来描述，当且仅当两个这样的表达式对于所有变量的取值都相等时，对应的电路具有相同的输入–输出行为。此外，每一种可能的输入–输出行为都可以通过合适的布尔表达式来建模。
• 二元布尔代数在布尔代数的一般理论中也非常重要，因为一个涉及多个变量的等式当且仅当在二元布尔代数中成立时，它才在所有布尔代数中普遍成立（对于变量数量较少的情况，可以通过一个简单的穷举算法来验证）。例如，可以用此方法证明以下定律（共识定理，Consensus theorems）在所有布尔代数中都是普遍成立的：
• $(a \lor b) \land (\lnot a \lor c) \land (b \lor c) \equiv (a \lor b) \land (\lnot a \lor c)$
• $(a \land b) \lor (\lnot a \land c) \lor (b \land c) \equiv (a \land b) \lor (\lnot a \land c)$
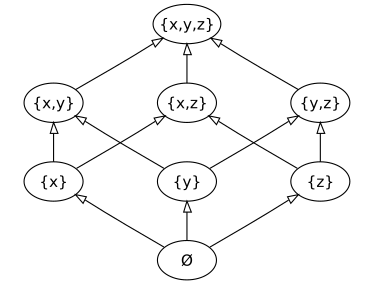
• 任意一个非空集合 $S$ 的幂集（即所有子集组成的集合）形成一个布尔代数，即集合代数，其两个运算分别是 $\lor := \cup$（并集）和 $\land := \cap$（交集）。最小元素 $0$ 是空集，最大元素 $1$ 是集合 $S$ 本身。
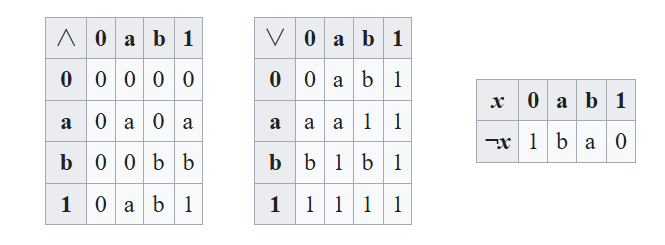
• 在二元布尔代数之后，最简单的布尔代数是由两个原子的幂集所定义的布尔代数：
  
  图 3
• 集合 $S$ 的所有有限子集或余有限子集组成的集合 $A$ 构成一个布尔代数，也是一个集合代数，称为有限–余有限代数。如果 $S$ 是无限集，那么 $S$ 的所有余有限子集组成的集合称为 Fréchet 滤子，它是 $A$ 上的一个自由超滤子。然而，Fréchet 滤子并不是 $S$ 的幂集上的超滤子。
• 从具有 $\kappa$ 个句子符号的命题演算出发，可以构造 Lindenbaum 代数（即命题演算中所有句子的集合，按逻辑等价类划分）。这一构造得到一个布尔代数，它实际上是在 $\kappa$ 个生成元上的自由布尔代数。命题演算中的一个真值赋值对应于从该代数到二元布尔代数的一个布尔代数同态。
• 对于任何具有最小元的线性有序集 $L$，区间代数是包含所有半开区间 $[a,b)$ 的最小布尔代数，其中 $a \in L$，而 $b$ 取自 $L$ 或等于 $\infty$。区间代数在研究 Lindenbaum–Tarski 代数中非常有用；每一个可数布尔代数都同构于某个区间代数。
  
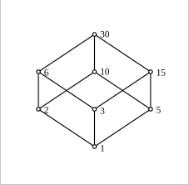
  图 4：30 的因子布尔代数的 Hasse 图。
• 对于任意自然数 $n$，其所有正因子构成的集合，定义 $a \le b$ 当且仅当 $a$ 整除 $b$，形成一个分配格。当且仅当 $n$ 是平方因子互素数时，该格才是一个布尔代数。这个布尔代数的最小元和最大元分别是自然数 1 和 $n$。元素 $a$ 的补元由 $n/a$ 给出。元素 $a$ 和 $b$ 的交与并分别由 $a$ 与 $b$ 的最大公因数和最小公倍数给出。环加法 $a + b$ 定义为 $$ \frac{\operatorname{lcm}(a, b)}{\operatorname{gcd}(a, b)}~ $$ 图中给出了 $n = 30$ 的一个例子。作为反例，考虑非平方因子互素数 $n = 60$，30 与其补元 2 的最大公因数是 2，而它本应是最小元 1。
• 布尔代数的其他例子来自拓扑空间：若 $X$ 是一个拓扑空间，则 $X$ 中所有既开又闭的子集组成的集合构成一个布尔代数，其运算为 $\lor := \cup$（并集）和 $\land := \cap$（交集）。
• 若 $R$ 是一个任意环，则其中心幂等元的集合，即 $$ A = \{ e \in R : e^2 = e \text{ 且 } ex = xe \text{ 对所有 } x \in R \text{ 成立} \},~ $$ 也构成布尔代数。

　　 当其运算定义为 $e \lor f := e + f - ef \quad \text{以及} \quad e \land f := ef$ 时，它就成为一个布尔代数。

4. 同态与同构

　　 两个布尔代数 $A$ 和 $B$ 之间的**同态**是一个函数 $f : A \to B$，使得对所有 $A$ 中的 $a, b$ 都有： $$ f(a \lor b) = f(a) \lor f(b),~ $$ $$ f(a \land b) = f(a) \land f(b),~ $$ $$ f(0) = 0,~ $$ $$ f(1) = 1~ $$ 由此可得，对于所有 $A$ 中的 $a$，都有 $f(\lnot a) = \lnot f(a)$。所有布尔代数及其同态所组成的类，在格范畴中构成一个充满子范畴。

　　 两个布尔代数 $A$ 和 $B$ 之间的同构是一个具有逆同态的同态 $f : A \to B$，即存在一个同态 $g : B \to A$，使得复合 $g \circ f : A \to A$ 是 $A$ 上的恒等函数，且复合 $f \circ g : B \to B$ 是 $B$ 上的恒等函数。一个布尔代数同态当且仅当它是双射时，才是一个同构。

5. 布尔环

　　 每一个布尔代数 $(A, \land, \lor)$ 都可以通过如下定义导出一个环 $(A, +, \cdot)$：$a + b := (a \land \lnot b) \lor (b \land \lnot a) = (a \lor b) \land \lnot(a \land b)$（在集合的情形下，这个运算称为对称差，在逻辑的情形下称为异或 XOR），以及 $a \cdot b := a \land b$。该环的零元与布尔代数中的 0 一致；该环的乘法单位元与布尔代数中的 1 一致。这个环具有性质 $a \cdot a = a$（对所有 $a \in A$），具有这一性质的环称为布尔环。反过来，若给定一个布尔环 $A$，可以通过定义 $x \lor y := x + y + (x \cdot y),\quad x \land y := x \cdot y$ 将其转化为一个布尔代数。\(^\text{[4][5]}\) 由于这两个构造互为逆过程，因此可以说每个布尔环都来自某个布尔代数，反之亦然。进一步地，一个映射 $f : A \to B$ 当且仅当它是布尔代数的同态时，它也是布尔环的同态。布尔环与布尔代数的范畴是等价的；\(^\text{[6]}\) 实际上，这两个范畴是同构的。Hsiang（1985）给出了一种基于规则的算法，用于检查两个任意表达式是否在所有布尔环中表示相同的值。更一般地，Boudet、Jouannaud 和 Schmidt-Schauß（1989）提出了一种算法，用于求解任意布尔环表达式之间的方程。利用布尔环与布尔代数的相似性，这两种算法在自动定理证明中都有应用。

6. 理想与滤子

　　 布尔代数 $A$ 的**理想**是一个非空子集 $I$，使得对所有 $x, y \in I$ 有 $x \lor y \in I$，并且对所有 $a \in A$ 有 $a \land x \in I$。这个理想的概念与布尔环 $A$ 中的环理想概念一致。一个理想 $I$ 称为素理想，如果 $I \neq A$ 并且总是有 $a \land b \in I \Rightarrow a \in I$ 或 $b \in I$。此外，对于任意 $a \in A$，有 $a \land -a = 0 \in I$，如果 $I$ 是素理想，那么对每个 $a \in A$，总有 $a \in I$ 或 $-a \in I$。一个理想 $I$ 称为极大理想，如果 $I \neq A$，并且唯一真包含 $I$ 的理想是 $A$ 本身。对于一个理想 $I$，如果 $a \notin I$ 且 $-a \notin I$，则 $I \cup \{a\}$ 或 $I \cup \{-a\}$ 包含于另一个真理想 $J$。因此，这样的 $I$ 不是极大的，所以在布尔代数中素理想与极大理想的概念是等价的。此外，这些概念与布尔环 $A$ 中的素理想与极大理想的环论概念一致。

　　 理想的对偶是滤子。布尔代数 $A$ 的一个滤子是一个非空子集 $p$，使得对所有 $x, y \in p$ 有 $x \land y \in p$，并且对所有 $a \in A$ 有 $a \lor x \in p$。布尔代数中极大（或素）理想的对偶是超滤子。超滤子也可以描述为从 $A$ 到二元布尔代数的二值同态。命题 “布尔代数中的每个滤子都可以扩展为一个超滤子” 称为超滤子引理，在 Zermelo–Fraenkel 集合论（ZF）中如果 ZF 一致，该命题无法被证明。在 ZF 中，超滤子引理严格弱于选择公理。超滤子引理有许多等价表述：每个布尔代数都有一个超滤子，布尔代数中的每个理想都可以扩展为一个素理想，等等。

7. 表示

　　 可以证明，每个有限布尔代数都同构于某个有限集合的所有子集构成的布尔代数。因此，每个有限布尔代数的元素个数都是 2 的幂。

　　 Stone 著名的布尔代数表示定理表明：每个布尔代数 $A$ 都同构于某个（紧致、全不连通、Hausdorff）拓扑空间中的所有闭开集构成的布尔代数。

8. 公理化

　　 最早的布尔格/布尔代数的公理化是由英国哲学家兼数学家阿尔弗雷德·诺思·怀特海（Alfred North Whitehead）于 1898 年提出的。[7][8] 其中包括上述公理，并另外加入了 $x \lor 1 = 1$ 和 $x \land 0 = 0$。1904 年，美国数学家爱德华·V·亨廷顿（Edward V. Huntington，1874–1952）给出了可能是最简洁的基于 $\land, \lor, \lnot$ 的公理化，甚至证明了结合律（见附框）。[9] 他还证明了这些公理彼此是独立的。[10] 1933 年，亨廷顿提出了如下优雅的布尔代数公理化方案。[11] 它只需要一个二元运算 $+$ 和一个一元函数符号 $n$（表示 “补”）即可，并且满足以下定律：

1. 交换律：$x + y = y + x$
2. 结合律：$(x + y) + z = x + (y + z)$
3. Huntington 方程：$n(n(x) + y) + n(n(x) + n(y)) = x$ 赫伯特·罗宾斯立即提出问题：如果用 Huntington 方程的对偶来代替它，即：
4. Robbins 方程**：$n(n(x + y) + n(x + n(y))) = x$

　　 那么 (1)、(2) 和 (4) 是否构成布尔代数的一个基础？称 (1)、(2) 和 (4) 满足的代数为 Robbins 代数，问题随之变为：是否每个 Robbins 代数都是布尔代数？这个问题（后来被称为 Robbins 猜想）悬而未决几十年，成为阿尔弗雷德·塔尔斯基及其学生们最喜爱的问题之一。1996 年，阿贡国家实验室的威廉·麦库恩，在拉里·沃斯、史蒂夫·温克和鲍勃·维罗夫等人的早期工作基础上，给出了肯定的答案：每个 Robbins 代数都是布尔代数。麦库恩证明的关键是他设计的计算机程序 EQP。关于麦库恩证明的简化版本，可参见 Dahn (1998)。

　　 进一步的工作还致力于减少布尔代数的公理数量，详见 布尔代数最小公理集。

9. 推广

　　 **去掉布尔代数公理中单位元存在性的要求，就得到了 “广义布尔代数”。** 形式上，如果一个分配格 $B$ 具有最小元 $0$，并且对任意 $a, b \in B$ 满足 $a \leq b$，都存在一个元素 $x$，使得 $a \land x = 0 \quad \text{且} \quad a \lor x = b$,则称 $B$ 是一个广义布尔格。定义 $a \setminus b$ 为唯一的元素 $x$，使得 $(a \land b) \lor x = a \quad \text{且} \quad (a \land b) \land x = 0$,则称结构 $(B, \land, \lor, \setminus, 0)$ 是一个广义布尔代数，而 $(B, \lor, 0)$ 是一个广义布尔半格。广义布尔格正好是布尔格的理想。

　　 满足布尔代数所有公理，除了两个分配律公理以外的结构，称为正交补格。正交补格在量子逻辑中自然出现，例如作为可分 Hilbert 空间闭线性子空间所成的格。

10. 另见

• 布尔代数主题列表
• 布尔域
• 布尔函数
• 布尔逻辑
• 布尔环
• 布尔值函数
• 规范形式（布尔代数）
• 完全布尔代数
• 德摩根律
• 强迫（数学）
• 自由布尔代数
• Heyting 代数
• 超立方体图
• 卡诺图
• 形式定律
• 逻辑门
• 逻辑图
• 逻辑矩阵
• 命题逻辑
• 奎因–麦克拉斯基算法
• 二元布尔代数
• 维恩图
• 条件事件代数

11. 注

1. 严格来说，电气工程师倾向于使用额外的状态来表示电路的其他情况，例如高阻抗。参见 IEEE 1164 或 IEEE 1364。

12. 参考文献

1. Givant & Halmos 2009，第 20 页。
2. Davey & Priestley 1990，第 109、131、144 页。
3. Goodstein 2012，第 21 页及以下。
4. Stone 1936。
5. Hsiang 1985，第 260 页。
6. Cohn 2003，第 81 页。
7. Padmanabhan & Rudeanu 2008，第 73 页。
8. Whitehead 1898，第 37 页。
9. Huntington 1904，第 292–293 页。
10. Huntington 1904，第 296 页。
11. Huntington 1933a。

引用著作

• Davey, B.A.; Priestley, H.A. (1990). Introduction to Lattices and Order. Cambridge Mathematical Textbooks. Cambridge University Press.
• Cohn, Paul M. (2003). Basic Algebra: Groups, Rings, and Fields. Springer, 第 51、70–81 页, ISBN 9781852335878.
• Givant, Steven; Halmos, Paul (2009). Introduction to Boolean Algebras. Undergraduate Texts in Mathematics. Springer, ISBN 978-0-387-40293-2.
• Goodstein, R. L. (2012). “第 2 章: 自对偶公理系统 (The self-dual system of axioms)”, Boolean Algebra. Courier Dover Publications, 第 21 页及以下, ISBN 9780486154978.
• Hsiang, Jieh (1985). “Refutational Theorem Proving Using Term Rewriting Systems”. Artificial Intelligence. 25 (3): 255–300. doi:10.1016/0004-3702(85)90074-8.
• Huntington, Edward V. (1904). “Sets of Independent Postulates for the Algebra of Logic”. Transactions of the American Mathematical Society. 5 (3): 288–309. doi:10.1090/s0002-9947-1904-1500675-4. JSTOR 1986459.
• Padmanabhan, Ranganathan; Rudeanu, Sergiu (2008). Axioms for lattices and boolean algebras. World Scientific, ISBN 978-981-283-454-6.
• Stone, Marshall H. (1936). “The Theory of Representations for Boolean Algebra”. Transactions of the American Mathematical Society. 40: 37–111. doi:10.1090/s0002-9947-1936-1501865-8.
• Whitehead, A.N. (1898). A Treatise on Universal Algebra. Cambridge University Press. ISBN 978-1-4297-0032-0.

常用参考文献

• Brown, Stephen; Vranesic, Zvonko (2002), Fundamentals of Digital Logic with VHDL Design (第 2 版), McGraw–Hill, ISBN 978-0-07-249938-4. 见第 2.5 节。
• Boudet, A.; Jouannaud, J.P.; Schmidt-Schauß, M. (1989). "Unification in Boolean Rings and Abelian Groups". Journal of Symbolic Computation. 8 (5): 449–477. doi:10.1016/s0747-7171(89)80054-9.
• Cori, Rene; Lascar, Daniel (2000), Mathematical Logic: A Course with Exercises, Oxford University Press, ISBN 978-0-19-850048-3. 见第 2 章。
• Dahn, B. I. (1998), "Robbins Algebras are Boolean: A Revision of McCune's Computer-Generated Solution of the Robbins Problem", Journal of Algebra, 208 (2): 526–532, doi:10.1006/jabr.1998.7467.
• Halmos, Paul (1963), Lectures on Boolean Algebras, Van Nostrand, ISBN 978-0-387-90094-0.
• Halmos, Paul; Givant, Steven (1998), Logic as Algebra, Dolciani Mathematical Expositions, vol. 21, Mathematical Association of America, ISBN 978-0-88385-327-6.
• Huntington, E. V. (1933a), "New sets of independent postulates for the algebra of logic" (PDF), Transactions of the American Mathematical Society, 35 (1), American Mathematical Society: 274–304, doi:10.2307/1989325, JSTOR 1989325.
• Huntington, E. V. (1933b), "Boolean algebra: A correction", Transactions of the American Mathematical Society, 35 (2): 557–558, doi:10.2307/1989783, JSTOR 1989783.
• Mendelson, Elliott (1970), Boolean Algebra and Switching Circuits, Schaum's Outline Series in Mathematics, McGraw–Hill, ISBN 978-0-07-041460-0.
• Monk, J. Donald; Bonnet, R., 编 (1989), Handbook of Boolean Algebras, North-Holland, ISBN 978-0-444-87291-3. 共 3 卷。(Vol.1: ISBN 978-0-444-70261-6, Vol.2: ISBN 978-0-444-87152-7, Vol.3: ISBN 978-0-444-87153-4)
• Sikorski, Roman (1966), Boolean Algebras, Ergebnisse der Mathematik und ihrer Grenzgebiete, Springer Verlag.
• Stoll, R. R. (1963), Set Theory and Logic W. H. Freeman, ISBN 978-0-486-63829-4. 1979 年由 Dover Publications 再版。

13. 外部链接

• "Boolean algebra", Encyclopedia of Mathematics, EMS Press, 2001 [1994]。
• Stanford Encyclopedia of Philosophy: "The Mathematics of Boolean Algebra", 作者 J. Donald Monk。
• McCune, W. (1997). Robbins Algebras Are Boolean. Journal of Automated Reasoning (JAR), 19(3): 263–276。
• "Boolean Algebra", 作者 Eric W. Weisstein, Wolfram Demonstrations Project, 2007。
• Burris, Stanley N.; Sankappanavar, H. P. (1981). A Course in Universal Algebra. Springer-Verlag. ISBN 3-540-90578-2。
• Weisstein, Eric W. "Boolean Algebra". MathWorld。