玻尔兹曼因子（综述）

                     

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章。

图
图 1：玻尔兹曼分布是一个指数分布。

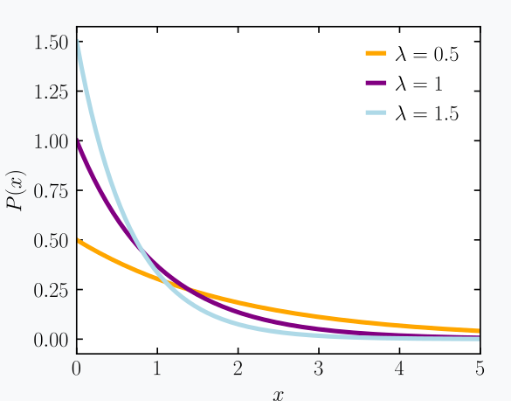
　　 在统计力学和数学中，玻尔兹曼分布（也称为吉布斯分布 \(^\text{[1]}\)）是一种概率分布或概率测度，用于描述一个系统处于某一状态的概率，它是该状态能量和系统温度的函数。该分布的形式为： \[ p_i \propto \exp\left(-\frac{\varepsilon_i}{kT}\right)~ \] 其中：\( p_i \) 是系统处于状态 \( i \) 的概率；\( \exp \) 是指数函数；\( \varepsilon_i \) 是该状态的能量；常数 \( kT \) 是玻尔兹曼常数 \( k \) 与热力学温度 \( T \) 的乘积。符号 \( \propto \) 表示成比例关系（关于比例常数的具体内容，见 “分布” 一节）。

图
图 2：玻尔兹曼因子 \( \frac{p_i}{p_j} \)（纵轴）作为温度 T 的函数，针对几个能量差 \( \epsilon_i - \epsilon_j \)。”

　　 这里的 “系统” 一词具有广泛的含义；它可以指从 “足够数量” 的原子或单个原子 \(^\text{[1]}\) 到像天然气储罐这样的宏观系统。因此，玻尔兹曼分布可以用于解决各种各样的问题。该分布表明，能量较低的状态总是具有更高的被占据的概率。

　　 两个状态的概率之比被称为玻尔兹曼因子，其特征是仅依赖于这两个状态的能量差： \[ \frac{p_i}{p_j} = \exp\left(\frac{\varepsilon_j - \varepsilon_i}{kT}\right)~ \] 玻尔兹曼分布以路德维希·玻尔兹曼的名字命名，他最早于 1868 年在研究热平衡状态下气体的统计力学时提出了这一分布。\(^\text{[2]}\) 玻尔兹曼的统计工作体现在他的论文《论机械热理论的第二基本定理与关于热平衡条件的概率计算之间的关系》中。\(^\text{[3]}\) 之后，约西亚·威拉德·吉布斯于 1902 年在其现代通用形式上对该分布进行了深入研究。\(^\text{[4]}\)

　　 玻尔兹曼分布不应与麦克斯韦–玻尔兹曼分布或麦克斯韦-玻尔兹曼统计混淆。玻尔兹曼分布给出了系统处于某一状态的概率，作为该状态能量的函数[5]，而麦克斯韦-玻尔兹曼分布给出了理想气体中粒子速度或能量的概率。然而，一维气体中的能量分布确实遵循玻尔兹曼分布。

1. 分布

　　 玻尔兹曼分布是一种概率分布，它给出了某一状态的概率，作为该状态能量和分布所应用的系统的温度的函数 \(^\text{[6]}\)。它的表达式为： \[ p_i = \frac{1}{Q} \exp\left(-\frac{\varepsilon_i}{kT}\right) = \frac{\exp\left(-\frac{\varepsilon_i}{kT}\right)}{\sum _{j=1}^{M}\exp\left(-\frac{\varepsilon_j}{kT}\right)}~ \] 其中：

　　 \[{\displaystyle Q=\sum _{j=1}^{M}\exp \left(-{\tfrac {\varepsilon _{j}}{kT}}\right)}~\] 这来自于所有可达状态的概率必须加起来等于 1 的约束。

　　 使用拉格朗日乘子法，可以证明玻尔兹曼分布是最大化熵的分布： \[ S(p_1, p_2, \cdots, p_M) = -\sum_{i=1}^{M} p_i \log_2 p_i~ \] 在归一化约束条件下，即 \(\sum p_i = 1\) 以及约束条件下，即 \(\sum p_i \varepsilon_i\) 等于一个特定的平均能量值，除了两种特殊情况。（这些特殊情况出现在平均值是能量 \(\varepsilon_i\) 的最小值或最大值时。在这些情况下，最大化熵的分布是玻尔兹曼分布的极限，其中 \(T\) 分别从上方或下方趋近于零。）

　　 如果我们知道系统可达状态的能量，分配函数就可以计算出来。对于原子，分配函数的值可以在 NIST 原子光谱数据库中找到。\(^\text{[7]}\)

　　 该分布表明，能量较低的状态总是比能量较高的状态具有更高的占据概率。它还可以为我们提供两种状态被占据的概率之间的定量关系。状态 i 和 j 的概率比率可以表示为： \[ \frac{p_i}{p_j} = \exp \left( \frac{\varepsilon_j - \varepsilon_i}{kT} \right)~ \] 其中：

　　 能量级别的人口比率还必须考虑它们的简并度。

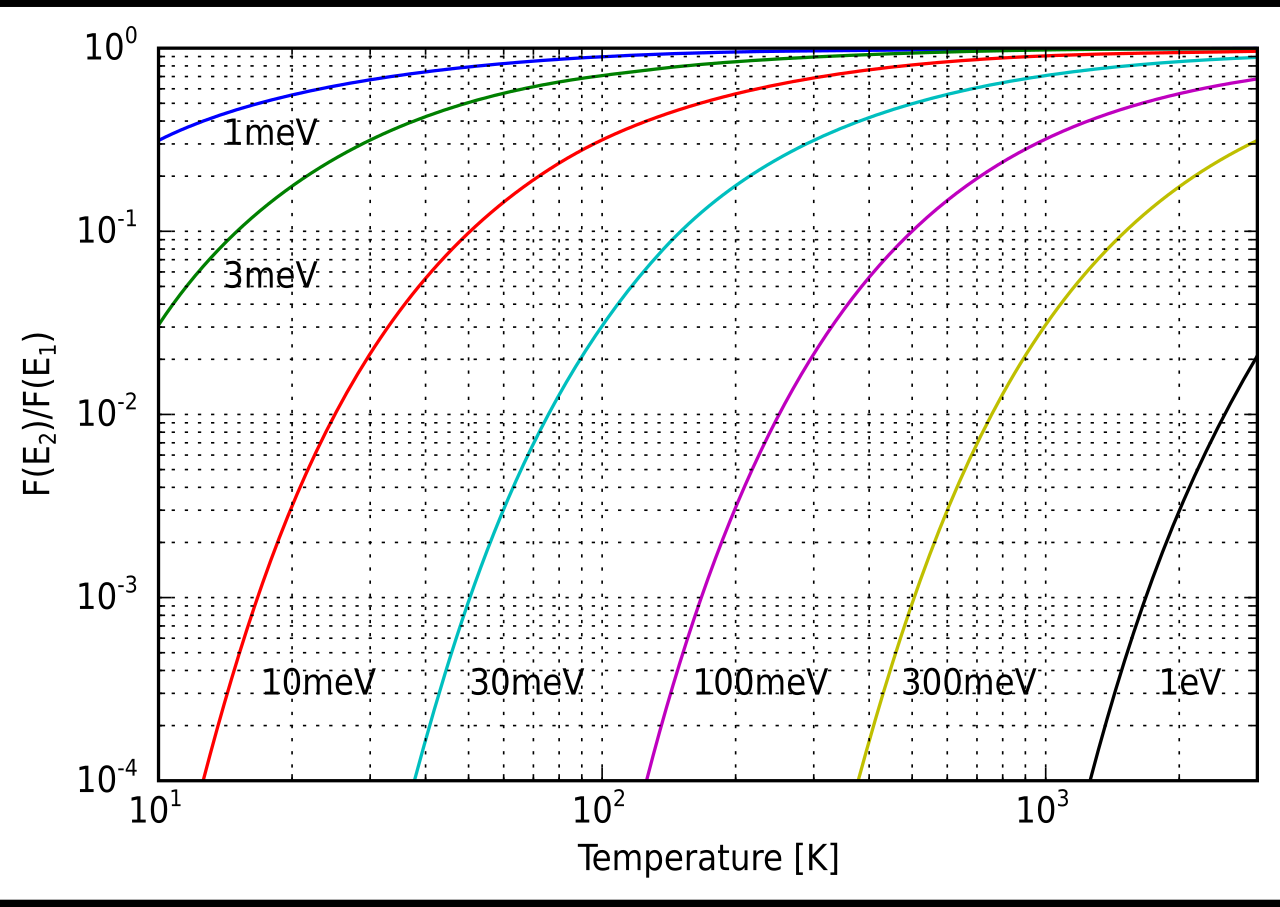
　　 玻尔兹曼分布常用于描述粒子（如原子或分子）在其可达的束缚态上的分布。如果我们有一个由许多粒子组成的系统，粒子处于状态 \(i\) 的概率实际上是这样的概率：如果我们从该系统中随机挑选一个粒子并检查它处于什么状态，那么我们发现它处于状态 \(i\)。这个概率等于状态 \(i\) 中的粒子数除以系统中粒子的总数，也就是占据状态 \(i\) 的粒子的比例。 \[ p_i = \frac{N_i}{N}~ \] 其中 \( N_i \) 是状态 \(i\) 中的粒子数，\( N \) 是系统中粒子的总数。我们可以使用玻尔兹曼分布来求得这个概率，即我们已经看到的，它等于处于状态 i 的粒子的比例。因此，给出状态 \(i\) 中粒子比例的方程是 \(^\text{[5]}\)： \[ \frac{N_i}{N} = \frac{\exp \left( -\frac{\varepsilon_i}{kT} \right)}{\sum_{j=1}^{M} \exp \left( -\frac{\varepsilon_j}{kT} \right)}~ \] 这个方程对于光谱学非常重要。在光谱学中，我们观察原子或分子从一种状态到另一种状态的跃迁所产生的光谱线。\(^\text{[5][8]}\) 为了使这一过程成为可能，必须有一些粒子处于初始状态以进行跃迁。我们可以通过计算处于初始状态的粒子比例来判断这个条件是否成立。如果比例微不足道，那么在该温度下进行计算时，跃迁很可能不会被观察到。一般来说，初始状态中分子比例越大，跃迁到第二状态的数量就越多。\(^\text{[9]}\) 这会产生更强的光谱线。然而，还有其他因素会影响光谱线的强度，例如它是否由允许的跃迁或禁止的跃迁引起。

　　 在机器学习中常用的 softmax 函数与玻尔兹曼分布有关： \[ (p_1, \ldots, p_M) = \operatorname{softmax} \left[ -\frac{\varepsilon_1}{kT}, \ldots, -\frac{\varepsilon_M}{kT} \right]~ \]

2. 广义玻尔兹曼分布

　　 形式为 \[ \Pr \left(\omega \right) \propto \exp \left[ \sum_{\eta =1}^{n} \frac{X_{\eta} x_{\eta}^{(\omega)}}{k_B T} - \frac{E^{(\omega)}}{k_B T} \right]~ \] 被一些作者称为广义玻尔兹曼分布。\(^\text{[10]}\)

　　 玻尔兹曼分布是广义玻尔兹曼分布的一个特例。广义玻尔兹曼分布在统计力学中用于描述经典系综、大系综和等温等压系综。广义玻尔兹曼分布通常是从最大熵原理推导出来的，但也有其他的推导方法。\(^\text{[10][11]}\)

　　 广义玻尔兹曼分布具有以下特性：

3. 在统计力学中

　　 玻尔兹曼分布出现在统计力学中，当考虑处于热平衡（即能量交换平衡）的固定组成的封闭系统时。最一般的情况是正则系综的概率分布。一些特殊情况（可从正则系综推导出）展示了玻尔兹曼分布的不同方面：

　　 正则系综（一般情况）

　　 正则系综给出了处于热平衡、与热库接触的固定体积封闭系统的各种可能状态的概率。正则系综具有玻尔兹曼形式的状态概率分布。

　　 子系统状态的统计频率（在非相互作用集合中）

　　 当研究的系统是由许多非相互作用的较小子系统组成的集合时，有时需要找到给定子系统状态在整个集合中的统计频率。正则系综在应用于此类集合时具有可分性特性：只要非相互作用的子系统具有固定的组成，那么每个子系统的状态都是独立的，并且也由正则系综来描述。因此，子系统状态的预期统计频率分布具有玻尔兹曼形式。

　　 经典气体的麦克斯韦–玻尔兹曼统计（非相互作用粒子系统）

　　 在粒子系统中，许多粒子共享同一空间，并且定期交换位置；它们占据的单粒子状态空间是共享的。麦克斯韦–玻尔兹曼统计给出了在热平衡下，非相互作用粒子的经典气体中，给定单粒子状态中粒子的预期数目。这一预期数目分布具有玻尔兹曼形式。

　　 尽管这些情况有很强的相似性，但区分它们仍然很有帮助，因为当关键假设发生变化时，它们的推广方式不同：

4. 在数学中

5. 在经济学中

　　 玻尔兹曼分布可以用于分配排放交易中的许可证。\(^ \boldsymbol{\mathbf{[13][14]}} \) 使用玻尔兹曼分布的新分配方法可以描述多国之间排放许可证的最可能、自然和无偏分配。

　　 玻尔兹曼分布与多项式对数选择模型具有相同的形式。作为一种离散选择模型，这在经济学中非常著名，因为丹尼尔·麦克法登将其与随机效用最大化联系了起来。\(^ \boldsymbol{\mathbf{[15]}} \)

6. 参见

7. 参考文献

  1. Landau, Lev Davidovich & Lifshitz, Evgeny Mikhailovich (1980) [1976]. *统计物理学* (理论物理学课程，第 5 卷，第 3 版)。牛津：Pergamon Press. ISBN 0-7506-3372-7. 由 J.B. Sykes 和 M.J. Kearsley 翻译。见第 28 节
  2. Boltzmann, Ludwig (1868). "Studien über das Gleichgewicht der lebendigen Kraft zwischen bewegten materiellen Punkten" [关于运动物质点之间生力平衡的研究]。维也纳报告，58: 517–560.
  3. "Archived copy" (PDF). 2021-03-05 从原文存档（PDF）。于 2017-05-11 检索。
  4. Gibbs, Josiah Willard (1902). *统计力学中的基本原理*。纽约：Charles Scribner's Sons.
  5. Atkins, P. W. (2010). *量子*，W. H. Freeman and Company，纽约。
  6. McQuarrie, A. (2000). *统计力学*。加利福尼亚州索萨利托：University Science Books. ISBN 1-891389-15-7.
  7. NIST 原子光谱数据库 级别表格，来自 nist.gov
  8. Atkins, P. W.; de Paula, J. (2009). *物理化学* (第 9 版)。牛津：Oxford University Press. ISBN 978-0-19-954337-3.
  9. Skoog, D. A.; Holler, F. J.; Crouch, S. R. (2006). *仪器分析原理*。马萨诸塞州波士顿：Brooks/Cole. ISBN 978-0-495-12570-9.
  10. Gao, Xiang; Gallicchio, Emilio; Roitberg, Adrian (2019). "广义玻尔兹曼分布是唯一使吉布斯-香农熵等于热力学熵的分布"。《化学物理学杂志》，151(3): 034113. arXiv:1903.02121. Bibcode:2019JChPh.151c4113G. doi:10.1063/1.5111333. PMID 31325924. S2CID 118981017.
  11. Gao, Xiang (2022 年 3 月). "系综理论的数学"。《物理学结果》，34: 105230. arXiv:2006.00485. Bibcode:2022ResPh..3405230G. doi:10.1016/j.rinp.2022.105230. S2CID 221978379.
  12. 一个经典的例子是磁性有序。非相互作用自旋的系统表现出可以通过单粒子正则系综理解的顺磁行为（得到布里渊函数）。相互作用的自旋系统则可能表现出更复杂的行为，如铁磁性或反铁磁性。
  13. Park, J.-W., Kim, C. U. 和 Isard, W. (2012). 使用玻尔兹曼分布进行排放交易中的许可证分配。《物理学 A》，391: 4883–4890.
  14. 《公平分配的棘手问题》。技术评论博客。2011 年 8 月 17 日。引用并总结了 Park、Kim 和 Isard（2012）的内容。
  15. Amemiya, Takeshi (1985). "多项式对数选择模型"。《高级计量经济学》。牛津：Basil Blackwell. 第 295-299 页。ISBN 0-631-13345-3.

致读者： 小时百科一直以来坚持所有内容免费无广告，这导致我们处于严重的亏损状态。 长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。 因此，我们请求广大读者热心打赏 ，使网站得以健康发展。 如果看到这条信息的每位读者能慷慨打赏 20 元，我们一周就能脱离亏损， 并在接下来的一年里向所有读者继续免费提供优质内容。 但遗憾的是只有不到 1% 的读者愿意捐款， 他们的付出帮助了 99% 的读者免费获取知识， 我们在此表示感谢。

                     

友情链接： 超理论坛　|　©小时科技 保留一切权利