北京科技大学 2006 年考研普通物理 A 卷

贡献者： 待更新

　　 声明：“该内容来源于网络公开资料，不保证真实性，如有侵权请联系管理员”

　　 适用专业：凝聚态物理、物理电子学

1. 选择题

1. 质点作半径为 R 的变速圆周运动的加速度大小为(v 表示任一时刻质点的速率)
   (A) $\displaystyle \frac{\mathrm{d}{v}}{\mathrm{d}{t}} $
   (B) $\displaystyle \frac{v^2}{R}$
   (C) $\displaystyle \frac{\mathrm{d}{v}}{\mathrm{d}{t}} +\frac{v^2}{R}$
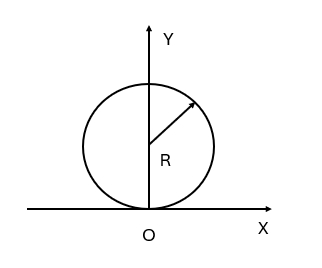
   (D) $\displaystyle [( \frac{\mathrm{d}{v}}{\mathrm{d}{t}} )+\frac{v^4}{R^2}]^\frac{1}{2}$
2. 一质点在如图 1 所示的坐标平面内作圆周运动，有一力 $\vec F=F_0(x\vec i+y \vec j)$ 作用在质点上，在该质点从坐标原点运动到 $(0,2R)$ 位置过程中，此力 $\vec F$ 下对它作的功为:
   
   
   图 1
   (A) $F_0R^2S$
   (B) $2F_0R^2$
   (C) $3F_0R^2$
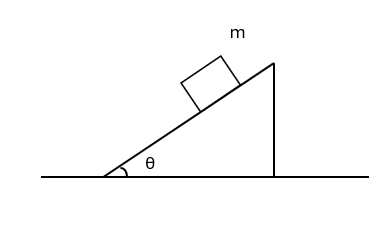
   (D) $4F_0R^2$
3. 若一倾角为 $\theta$ 的斜面上放一质量为 m 的物体，m 与斜面间的摩擦系数为 $\mu$，斜面向左加速运动，欲使 m 沿斜面向上滑动，则斜面的加速度值至少应为:
   
   
   图 2
   (A) $\displaystyle \frac{(\mu \cos \theta+\sin \theta)g}{\cos 2\theta -\mu \sin \theta}$
   (B) $\displaystyle\frac{(\mu \sin \theta+\cos \theta)g}{\cos 2\theta -\mu \sin \theta}$
   (C) $\displaystyle \frac{(\mu \cos \theta+\sin \theta)g}{\sin \theta -\mu \cos\theta}$
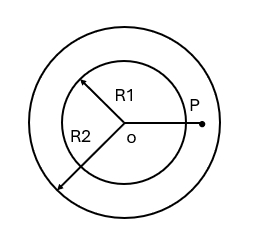
   (D)$\displaystyle \frac{(\mu \cos \theta+\sin \theta)g}{\cos \theta -\mu \sin\theta}$
4. 如图所示，两个同心球壳。内球半径为 $R_1$，均带有电荷 $Q$；外求壳半径为 $R_2$，壳的厚度忽略，原先不带电，但与地相连接。设地为电势零点，则在两球之间，距离球心为 $r$ 的 $P$ 点处电场强度的大小与电势分别为：
   
   
   图 3
   (A) $\displaystyle E=\frac{Q}{4\pi\varepsilon_0 r^2},U=\frac{Q}{4\pi\varepsilon_0 r}$
   (B) $\displaystyle E=\frac{Q}{4\pi\varepsilon_0 r^2},U=\frac{Q}{4\pi\varepsilon_0} (\frac{1}{R_1}-\frac{1}{r})$
   (C) $\displaystyle E=\frac{Q}{4\pi\varepsilon_0 r^2},U=\frac{Q}{4\pi\varepsilon_0} (\frac{1}{r}-\frac{1}{R_2}) $
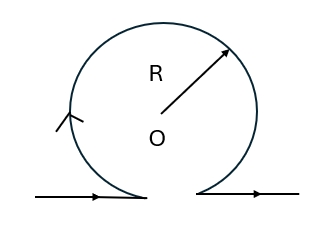
   (D)$\displaystyle E=0,\qquad U=\frac{Q}{4 \pi \varepsilon_0 R_2}$
5. 无限长直导线在 $P$ 处弯成半径为 $R$ 的圆，当通以电流 $I$ 时，则在圆心 $O$ 点的磁场感应强度大小等于
   
   
   图 4
   (A) $\displaystyle \frac{\mu_0 I}{2 \pi R}$
   (B) $\displaystyle \frac{\mu_0 I}{4R}$
   (C) $0$
   (D) $\displaystyle \frac{\mu_0 I}{2R}(1-\frac{1}{\pi})$
6. 已知一定量的某种理想气体，在温度为 $T_1$ 和 $T_2$ 时的分子最概然速率分别为 $V_{p1}$ 和 $V_{p2}$，分子速率分布的最大值分别为 $f(V_{p1})$ 和 $f(V_{p2})$。若 $T_1>T_2$，则
   (A) $V_{p1}>V_{p2},f(V_{p1}>f(V_{p2})$
   (B)$V_{p1}>V_{p2},f(V_{p1}< f(V_{p2})$
   (C)$V_{p1}< V_{p2},f(V_{p1}>f(V_{p2})$
   (D)$V_{p1}< V_{p2},f(V_{p1}< f(V_{p2})$
   

   2. 填空题

7. 一质量为 $M$ 的物体沿 $x$ 轴止向运动，假设该质点在通过坐标为 $x$ 的位置时速度的大小为 $kx$($k$ 为正值常量)，则此时作用于该质点上力 $F=()$，该质点从 $x=x_0$ 点出发运动到 $x=x_1$ 处所经历的时间 $\Delta t=()$
   
8. 把一个均匀带有电荷 $+Q$ 的球形肥皂泡由半径 $r_1$ 吹胀到 $r_2$，则半径为 $R(r_1< R< r_2)$ 的任一点的场强大小 $E$ 由 $(\qquad)$ 变为 $(\qquad)$;电势 $U$ 由 $(\qquad)$。(选无穷远处为电势零点)。
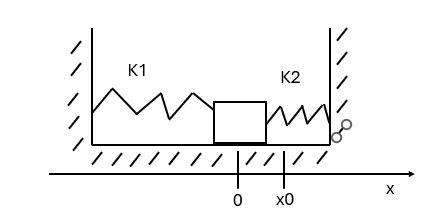
9. 如图所示，一质量为 $m$ 的滑块，两边分别与劲度系数为 $kl$ 和 $k2$ 的轻弹簧相连，两弹簧的另外两端分别规定在墙上。滑块 $m$ 可在光滑的水平面上滑动,$0$ 点为系统的平衡位置，将滑块向右移动到 $x0$，自静止释放，并从释放时开始计时。取坐标如图所示，则其振动方程为:$(\qquad)$
   
   图 5
10. 在弦线上有一简谐波，其表达式为:$y_1=2.0*10^{-2} \cos[100\pi(t+\frac{x}{20})-\frac{4}{3}\pi]$,为了在此弦线上形成驻波，并且 $x=0$ 处为一波腹，此弦线上还应有一简谐波，其表达式为：$(\qquad)$
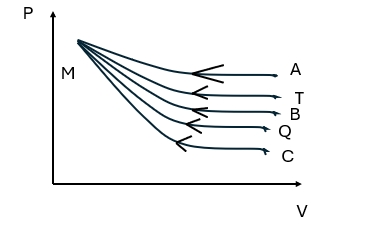
11. 右图为一理想气体几种状态变化过程的 $p-V$ 图，其中 $MT$ 为等温线，$MQ$ 为绝热线，在 $AM,BM,CM$ 三种准静态过程中：
    
    
    图 6
    温度升高的是 $(\qquad)$ 过程，
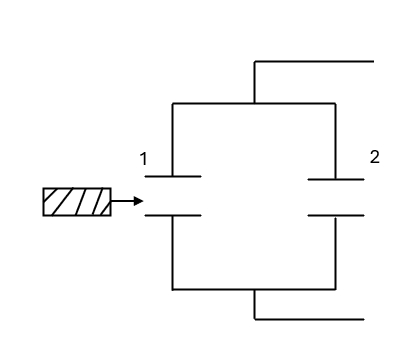
    气体吸热的是 $(\qquad)$ 过程。
12. $1,2$ 是两个完全相同的空气电容器，将其充电后与电源断开，再将一块各向同性均匀电介质板插入电容器 $1$ 的两极板间，如图所示。则电容器 $2$ 的电压 $U_2$,电场能量 $W_2$ 如何变化？(填增大，减小或不变)
    
    
    图 7
    $U_2(\qquad)$
    $W_2(\qquad)$
13. 光波的干涉是指 $(\qquad)$,相干条件为 $(\qquad)$。
14. 用平行的白光垂入射在平面透射光栅上时，波长为 $\lambda_1=440nm $ 的第三级光谱线将与波长为 $\lambda_2=(\quad)nm$ 的第二级光谱线重叠 $(1nm=10^{-9}m)$。
15. 一束自然光垂直穿过两个偏振片，两个偏振片的偏振化方向成 $45$°角，已知通过此两偏振片后的光强为 $1$ ,则入射至第二个偏振片的线偏振光强度为 $(\qquad)$。

    3. 计算题

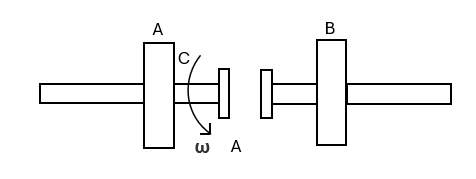
16. (此题单考生不做！)如图所示，$A$ 和 $B$ 两飞轮的轴杆在同一中心线上，设两轮的转动惯量分别为 $J=10kg.m^2$ 和 $J=20kg.m^2$。开始时，$A$ 轮的转速为 $600rev/min$，$B$ 轮静止，$C$ 为摩擦齿和器，其转动惯量可忽略不计。$A,B$ 分别与 $C$ 的左右两个两个组件相连，当 $C$ 的左右组件齿合时，$B$ 轮得到加速而 $A$ 轮减速，直到两轮的转速相等为止。设轴光滑，求:
    
    
    图 8
    (1)两轮齿合后的转速 $n$;
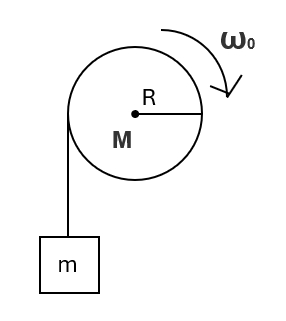
    (2)两轮各自所受的冲量矩。
17. (此题统考生不做！)一轴承光滑的定滑轮，质量为 $M=2.00kg$，半径为 $ R=0.10m$。一根不能伸长的轻绳。一端固定在定滑轮上，另一端系有一质量为 $m=5.00kg $ 的物体，如图所示。已知定滑轮的转动的初角速度 $\omega_0=1.00 rad/s$,方向垂直纸面向里。求:
    
    
    图 9
    (1)定滑轮角加速度的大小和方向;
    (2)定滑轮的角速度变化到 $\omega=0$ 时，物体上升的高度;
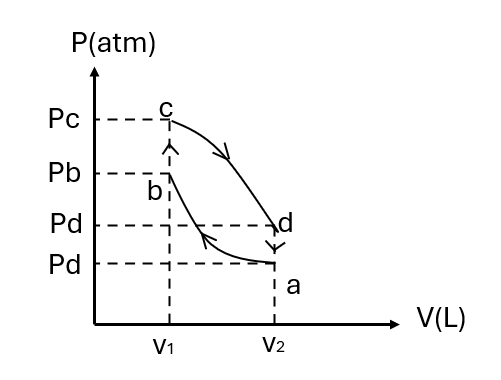
    (3)当物体回到原来位置时，定滑轮的角速度的大小和方向。
18. $1 mol $ 的氦气作如图所示的可逆循环，其中 $ ab $ 和 $cd$ 是绝热过程，$bc$ 和 $da$ 为等容过程，已知 $V_1=16.4L,V_2=32.8L,p_a=l atm,p_b=3.18 atm,p_c=4 atm. p_d=1.26 atm $ 试求:
    
    
    图 10
    (1)在各态氨气的温度;
    (2)在各态氨气的内能；
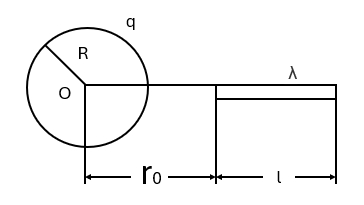
    (3)在一循环过程中氨气所做的净功。
19. (此题单考生不做！)如图所示，半径为 $R$ 的均匀带电球面，带有电荷 $q$。沿某一半径方向上有均匀带电细线，电荷线密度为 $\lambda$，长度为 $1$.细线左端离球心距离为 $r_0$。设球和线上的电荷分布不受相互作用影响。试求细线所受球面由荷的电场力和合细线在该电场中的电势能(设无穷远处的电势为零）。
    
    图 11
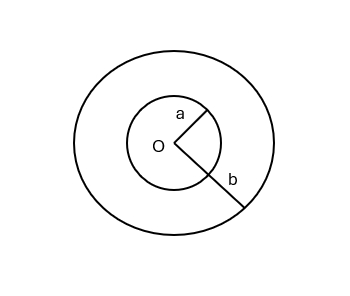
20. (此题统考生不做！)图示一球形电容器,在外球壳的半径 $b$ 和内外导体间的电势差 $U$ 维持条件下，求:
    
    
    图 12
    (1)两球壳之间的电场强度分布；
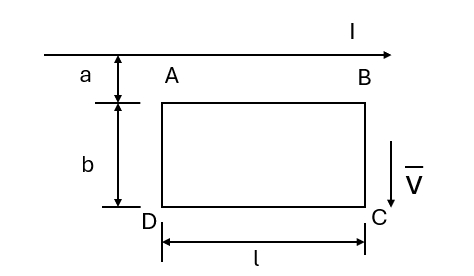
    (2)内球半径 $a$ 为多大时才能使内球表面附近的电场强度为最小?求这个最小电场强度的大小。
21. 载流长直导线与矩形回路 $ABCD$ 共面，导线平行于 $ AB$，如图所示。求下列情况下 $ABCD$ 中的感应电动势:
    
    
    图 13
    (1)长直导线中电流 $I=I_0$ 不变，$ABCD $ 以垂直于导线的速度 $v$ 远离导线匀速平移，当移动到图示位置时；
    (2)长直导线中电流 $I=I_0\sin \omega t$，$ABCD$ 不动;
    (3)长直导线中电流 $I=I_0\sin \omega t$，$ABCD$ 以垂直于导线的速度 $v$ 远离导线匀速运动，位置也如图。
22. 用波长为 $ 500nm(lnm=10^{-9}m)$ 的单色光垂直照射到由两块光学平玻璃构成的空气劈形膜上，在观察度射光的干涉现象中，距劈形模棱边 $l=1.56cm$ 的 $A$ 处是从棱边算起的第四条暗条纹中心。
    (1)求此劈形膜的劈尖角 $\theta$;
    (2)改用 $600nm$ 的单色光垂直照射到此劈尖上仍观察反射光的干涉条纹，$A$ 处是明条纹还是暗条纹？
    (3)在第(2)问的情形从棱边到 A 处的范围共有几条明纹？几条暗纹？