选择公理（综述）

                     

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章。

图
图 1：选择公理的示意图，其中每个集合 \( S_i \) 被表示为一个罐子，且其元素被表示为弹珠。每个元素 \( x_i \) 被表示为右侧的一个弹珠。颜色的使用旨在暗示在采用选择公理后，弹珠之间的函数关联。对于具有无限基数的集合，选择函数的存在通常与 ZF 系统无关，即使所有 \( S_i \) 都是有限的。

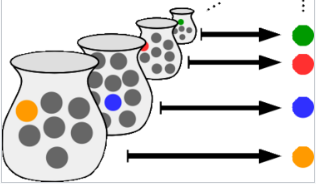
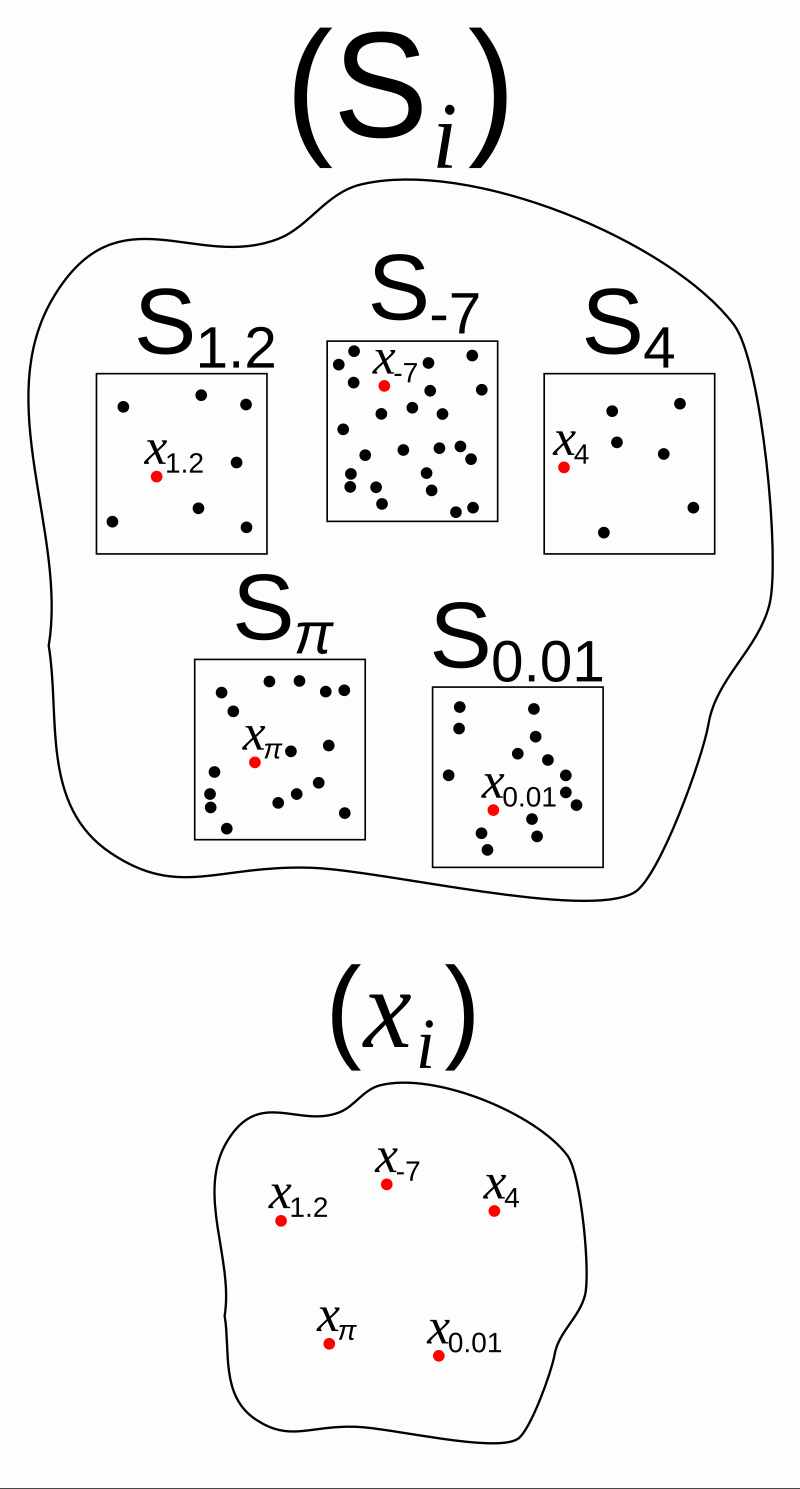
　　 在数学中，选择公理（简称 AC 或 AoC）是集合论的一个公理，它等价于 “非空集合的笛卡尔积是非空的” 这一命题。非正式地说，选择公理表明，给定任何一个集合的集合，每个集合至少包含一个元素，便可以通过从每个集合中选择一个元素来构造一个新集合，即使这个集合是无限的。形式上，它声明，对于每一个索引族 \( (S_i)_{i \in I} \) 的非空集合，存在一个索引集合 \( (x_i)_{i \in I} \)，使得对于每个 \( i \in I \)，都有 \( x_i \in S_i\)。\(^\text{[1]}\) 选择公理是由恩斯特·泽梅洛在 1904 年提出的，旨在形式化他的良序定理证明。选择公理等价于每个划分都有一个横切集的命题。\(^\text{[2]}\)

　　 在许多情况下，通过选择元素构造的集合可以在不使用选择公理的情况下完成，特别是当从中选择元素的集合个数是有限的，或者如果有一个标准规则来选择元素——即对于每个集合，存在某种区分性特性，恰好有一个元素满足该特性。一个典型的例子是从自然数中选取的集合。从这样的集合中，总是可以选择最小的数字，例如，给定集合 {{4, 5, 6}, {10, 12}, {1, 400, 617, 8000}}，包含每个集合最小元素的集合是 {4, 10, 1}。在这种情况下，“选择最小的数字” 就是一个选择函数。即使从自然数中收集了无限多个集合，也总是可以从每个集合中选择最小的元素来构造一个集合。也就是说，选择函数提供了所选元素的集合。但对于所有实数的非空子集的集合，尚未发现一个确定的选择函数。在这种情况下，必须调用选择公理。\(^\text{[3]}\)

图
图 2：\((S_i)\) 是一个以实数 \(\mathbb{R}\) 为索引的无限索引集合族；即，对于每个实数 \(i\)，都有一个集合 \(S_i\)，上面展示的是一个小样本。每个集合包含至少一个元素，且可能包含无限多个元素。选择公理允许我们从每个集合中选择一个元素，形成一个相应的元素族 \((x_i)\)，该族也以实数为索引，且每个 \(x_i\) 来源于 \(S_i\)。通常来说，这些集合可以通过任何集合 \(I\) 进行索引（称为索引集，其元素作为集合中元素的索引），不仅仅是 \(\mathbf{R}\)。

　　 伯特兰·罗素提出了一个类比：对于任何（即使是无限的）鞋子对的集合，可以从每对鞋子中挑选出左鞋，得到一个合适的鞋子集合（即集合）；这使得可以直接定义一个选择函数。而对于一对一对的袜子的无限集合（假设它们没有区分特征，如左袜子和右袜子），没有显而易见的方式来构造一个函数，从每对袜子中选择一只袜子来形成一个集合，而不使用选择公理。

　　 虽然最初具有争议，选择公理现在已被大多数数学家毫无保留地使用，\(^\text{[4]}\) 并且被包括在标准的公理化集合论中，即泽梅洛-弗兰克尔集合论与选择公理（ZFC）。这样做的动机之一是，许多广泛接受的数学结果，如提霍诺夫定理，要求选择公理来证明。现代集合论家还研究与选择公理不兼容的公理，如确定性公理。选择公理在某些构造性数学的变体中被避免，尽管在某些构造性数学的变体中，选择公理是被采纳的。

1. 陈述

　　 选择函数（也称为选择器或选择器函数）是一个定义在非空集合族 \(X\) 上的函数 \(f\)，满足对于 \(X\) 中的每个集合 \(A\)，\(f(A)\) 是 \(A\) 中的一个元素。基于这一概念，选择公理可以表述为：

　　 公理——对于任何非空集合族 \(X\)，存在一个选择函数 \(f\)，该函数定义在 \(X\) 上，并将 \(X\) 中的每个集合映射到该集合的一个元素。

　　 形式上，这可以表示为： \[ \forall X\left[\varnothing \notin X \implies \exists f\colon X \rightarrow \bigcup_{A \in X} A \quad \forall A \in X\,(f(A) \in A)\right].~ \] 因此，选择公理的否定可以表示为存在一个非空集合族，它没有选择函数。形式上，这可以通过利用以下逻辑等价关系来推导： \[ \neg \forall X\left[P(X) \to Q(X)\right] \quad \iff \quad \exists X\left[P(X) \land \neg Q(X)\right].~ \] 每个非空集合族 \(X\) 上的选择函数是 \(X\) 中集合的笛卡尔积的一个元素。这并不是笛卡尔积中最一般的情况，其中一个集合可以作为因子多次出现；然而，我们可以关注那些每次当某个集合作为因子出现时，选择相同元素的笛卡尔积中的元素，这些元素对应于该家族中所有不同集合的笛卡尔积的一个元素。选择公理断言存在这样的元素；因此，它等价于：

　　 给定任何非空集合族，它们的笛卡尔积是一个非空集合。

术语

　　 在本文及其他关于选择公理的讨论中，以下缩写是常见的：

变体

　　 选择公理有许多其他等价的表述。这些表述在集合论的其他基本公理的基础上，是等价的，即它们在选择公理的存在下能推导出选择公理，并且也能从选择公理中推导出来。

　　 一种变体通过实质上用每个选择函数的值域替代选择函数，避免了选择函数的使用：

　　 给定任何集合 \(X\)，如果空集不是 \(X\) 的元素，并且 \(X\) 中的元素两两不相交，则存在一个集合 \(C\)，使得它与 \(X\) 中的任何元素的交集恰好包含一个元素。[6] 这可以在一阶逻辑中形式化为： \[ \forall x \left( \exists e \left( e \in x \land \neg \exists y (y \in e) \right) \lor \exists a \exists b \exists c (a \in x \land b \in x \land c \in a \land c \in b \land \neg (a = b)) \lor \exists c \forall e \left( e \in x \implies \exists a \left( a \in e \land a \in c \land \forall b \left( (b \in e \land b \in c) \implies a = b \right) \right) \right) \right)~ \] 注意，\( P \lor Q \lor R \) 在逻辑上等价于 \((\neg P \land \neg Q) \implies R\)。

　　 用英语表达，这个一阶句子的意思是：
给定任何集合 \(X\)，
\(X\) 包含空集作为一个元素，或者
\(X\) 中的元素不是两两不相交的，或者
存在一个集合 \(X\)，使得它与 \(X\) 中的任何元素的交集恰好包含一个元素。

　　 这保证了对于任何集合 \(X\) 的划分，存在一个子集 \(C\) 属于 \(X\)，该子集从划分的每一部分中恰好选取一个元素。

　　 另一个等价的公理仅考虑那些本质上是其他集合的幂集的集合 \(X\)：

　　 对于任何集合 \(A\)，\(A\) 的幂集（去掉空集）有一个选择函数。 使用这个表述的作者通常会讨论 \(A\) 上的选择函数，但这与本文其他地方使用的选择函数的概念略有不同。这里的选择函数的定义域是 \(A\) 的幂集（去掉空集），因此适用于任何集合 \(A\)，而本文中其他地方使用的定义中，选择函数的定义域是一个集合族，因此仅适用于集合的集合。采用这种替代的选择函数概念，选择公理可以简洁地表述为：

　　 每个集合都有一个选择函数。\(^\text{[7]}\)

　　 这等价于：

　　 对于任何集合 \(A\)，存在一个函数 \(f : \mathcal{P}(A) \setminus \{\emptyset\} \to A\)，使得对于 \(A\) 的任何非空子集 \(B\)，都有 \(f(B) \in B\)。

　　 因此，选择公理的否定可以表示为：

　　 存在一个集合 \(A\)，使得对于 \(A\) 的所有函数 \(f\)（定义在 \(A\) 的非空子集上），存在一个子集 \(B\)，使得 \(f(B) \notin B\)。

对有限集合的限制

　　 选择公理的通常表述并没有规定非空集合的集合是有限的还是无限的，因此它暗示每个有限的非空集合族都有一个选择函数。然而，这个特定的情况是没有选择公理（ZF）的泽梅洛-弗兰克尔集合论的一个定理；它可以通过有限归纳法轻松证明。\(^\text{[8]}\) 在更简单的情况下，如果集合族只有一个集合，选择函数仅对应于该集合的一个元素，因此这个选择公理的实例表明每个非空集合都有一个元素；这一点显然成立。选择公理可以被视为这种性质的推广，已经在有限集合族中显现出来，扩展到任意集合族。

2. 使用

　　 直到 19 世纪末，选择公理常常是隐式使用的，尽管它还没有被正式表述。例如，在证明集合 \(X\) 只包含非空集合后，数学家可能会说 “令 \(F(s)\) 为 \(s \in X\) 的一个成员”，从而定义一个函数 \(F\)。一般来说，没有选择公理是无法证明 \(F\) 存在的，但在泽梅洛之前，这似乎没有引起注意。

3. 示例

　　 集合中各个非空集合的性质可能使得即便对于某些无限集合，也能够避免使用选择公理。例如，假设集合 \(X\) 中的每个成员都是自然数的非空子集。每个这样的子集都有一个最小元素，因此我们可以简单地规定我们的选择函数，将每个集合映射到该集合的最小元素。这就给出了从每个集合中选择一个元素的明确选择，并且不需要在我们的集合论公理中加入选择公理。

　　 当每个集合没有自然的选择元素时，问题就出现了。如果我们不能明确地做出选择，怎么知道我们的选择能构成一个合法的集合（根据其他泽梅洛-弗兰克尔集合论的公理定义）呢？例如，假设 \(X\) 是实数的所有非空子集的集合。首先，我们可能会尝试按 \(X\) 是有限集合的方式来进行。如果我们尝试从每个集合中选择一个元素，那么由于 \(X\) 是无限的，我们的选择过程将永远无法结束，因此我们将永远无法为所有的 \(X\) 生成一个选择函数。接下来我们可能会尝试指定每个集合的最小元素，但有些实数的子集没有最小元素。例如，开区间 \((0,1)\) 没有最小元素：如果 \(x \in (0,1)\)，那么 \(x/2\) 也在 \((0,1)\) 内，并且 \(x/2\) 总是严格小于 \(x\)。所以这个尝试也失败了。

　　 此外，考虑单位圆 \(S\) 和一个由所有有理数倍角的旋转组成的群 \(G\) 对 \(S\) 的作用。在这里，\(G\) 是可数的，而 \(S\) 是不可数的。因此，\(S\) 在 \(G\) 的作用下被分解成不可数多的轨道。使用选择公理，我们可以从每个轨道中选取一个点，得到一个不可数的子集 \(X\) 满足其所有的 \(G\)-平移都与 \(X\) 不交。那些平移的集合将圆分割成一个可数的、两两不相交的集合，这些集合都是两两全等的。由于 \(X\) 对于任何旋转不变的可数可加有限测度来说是不可测的，找到一个算法来从每个轨道选择一个点形成集合，要求我们在集合论的公理中加入选择公理。有关更多细节，参见不可测集合。

　　 在经典算术中，自然数是良序的：对于每个非空自然数子集，在自然排序下都有一个唯一的最小元素。通过这种方式，可以从给定的子集中指定一个集合。有人可能会说，“尽管实数的通常排序不起作用，但可能可以找到另一种排序，使得它是一个良序排序。然后，我们的选择函数可以在我们的非标准排序下选择每个集合的最小元素。” 问题就在于构造一个良序排序，而这显然需要选择公理才能确保其存在；当且仅当选择公理成立时，所有集合都可以良序化。

4. 批评与接受

　　 一个需要选择公理的证明可以证明某个对象的存在，但并没有在集合论的语言中明确构造该对象。例如，虽然选择公理暗示存在实数的良序化，但在某些包含选择公理的集合论模型中，并没有任何一个实数的良序化是可以定义的。同样，尽管可以使用选择公理证明存在一个不可列比的实数子集，但也可以证明，在某些情况下，根本没有这样的集合是可以定义的。\(^\text{[9]}\)

　　 选择公理断言这些难以捉摸的对象的存在（即证明存在的对象，但无法明确构造出来），这可能与某些哲学原则相冲突。\(^\text{[10]}\) 由于没有所有集合的标准良序化，依赖于良序化的构造可能不会产生标准的结果，即使期望产生标准的结果（例如，在范畴理论中常常如此）。这一点被用作反对使用选择公理的论据。

　　 另一个反对选择公理的论据是，它暗示存在一些看似违反直觉的对象。\(^\text{[11]}\) 一个例子是巴拿赫–塔尔斯基悖论，它表明可以将三维单位球体分解成有限多块，并且仅通过旋转和平移操作，将这些块重新组合成两个固体球，每个球的体积与原来的球相同。这种分解中使用选择公理构造的块是不可测的集合。

　　 尽管这些看似悖论的结果存在，但大多数数学家接受选择公理作为证明数学新结果的有效原理。但这场争论足够有趣，以至于当 ZFC（ZF 加选择公理）中的定理与选择公理在逻辑上等价（仅使用 ZF 公理）时，它被视为一个显著事件，数学家们也会寻找需要选择公理为假的结果，尽管这种推导类型不如需要选择公理为真的推导类型常见。

　　 ZF 的定理在该理论的任何模型中都成立，无论选择公理在该特定模型中的真假。选择公理及其弱版本的影响如下列出，因为它们不是 ZF 的定理。例如，巴拿赫–塔尔斯基悖论，单独从 ZF 中既无法证明也无法反驳：在 ZF 中无法构造所需的单位球分解，但也无法证明不存在这样的分解。这类陈述可以重新表述为条件语句——例如，“如果选择公理成立，则巴拿赫–塔尔斯基悖论中的分解存在。” 当原始陈述可以从 ZF 和选择公理中推导出来时，这类条件语句在 ZF 中是可以证明的。

5. 在构造性数学中

　　 如上所述，在经典的 ZFC 理论中，选择公理支持非构造性证明，其中某种类型的对象的存在被证明，但没有明确构造该实例。实际上，在集合论和拓扑论中，Diaconescu 定理表明选择公理暗示排中律。因此，这一原则在构造性集合论中不可用，因为构造性集合论使用的是非经典逻辑。

　　 当选择公理在马丁-洛夫类型理论中表述时，情况有所不同。在该理论中，以及高阶的海廷算术中，选择公理的适当表述是（根据不同的方法）作为公理被包含或可以作为定理被证明。\(^\text{[12]}\) 这种差异的原因在于，类型理论中的选择公理并不具备构造性集合论中选择公理所具备的外延性属性。\(^\text{[13]}\) 类型理论的背景将在下文进一步讨论。

　　 在构造性语境中，不同的选择原则已经得到了彻底的研究，且这些原则在不同学派和构造性数学的变体中的地位各不相同。构造性集合论中的一些结果使用了可数选择公理或依赖选择公理，这些公理并不暗示排中律。Errett Bishop，因其发展了构造性分析的框架而闻名，认为选择公理在构造性数学中是可接受的，并表示：

　　 “选择函数在构造性数学中是存在的，因为选择是由存在的含义本身所暗示的。”\(^\text{[14]}\)

　　 尽管可数选择公理在构造性数学中被广泛使用，但它的使用也受到了质疑。\(^\text{[15]}\)

6. 独立性

　　 早在 1922 年就有人知道，选择公理可能在包含原始元素的 ZF 变体中失败，这通过 Abraham Fraenkel 引入的置换模型技术得以实现，并由 Andrzej Mostowski 进一步发展。\(^\text{[16][17]}\) 基本技术可以如下说明：令 \(x_n\) 和 \(y_n\) 为不同的原始元素，其中 \(n = 1, 2, 3, \dots\)，然后构建一个模型，其中每个集合在除有限个 \(n\) 外都对 \(x_n \leftrightarrow y_n\) 置换对称。然后，集合 \(X = \{\{x_1, y_1\}, \{x_2, y_2\}, \{x_3, y_3\}, \dots\}\) 可以在该模型中，但像 \(\{x_1, x_2, x_3, \dots\}\) 这样的集合却不行，因此 \(X\) 不可能有选择函数。

　　 1938 年，\(^\text{[18]}\) 库尔特·哥德尔证明了选择公理的否定不是 ZF 的定理，通过构造一个内部模型（构造宇宙），使其满足 ZFC，从而表明如果 ZF 本身是一致的，则 ZFC 是一致的。1963 年，保罗·科恩利用为此目的发展出的强制技术，证明了假设 ZF 一致，选择公理本身不是 ZF 的定理。他通过构造一个更复杂的模型，满足 ZF¬C（ZF 加上选择公理的否定作为公理），从而证明 ZF¬C 是一致的。科恩的模型是一个对称模型，类似于置换模型，但使用自然数的 “通用” 子集（通过强制得以证明）替代原始元素。\(^\text{[19]}\)

　　 这些结果共同表明，选择公理在逻辑上与 ZF 独立。假设 ZF 一致是无害的，因为向一个已经不一致的系统添加另一个公理不会使情况变得更糟。由于独立性，是否在证明中使用选择公理（或其否定）不能通过引用集合论的其他公理来决定。必须基于其他理由做出决定。

　　 支持使用选择公理的一个论点是它非常方便，因为它允许证明一些否则无法证明的简化命题。许多可以使用选择公理证明的定理具有优雅的普遍性：任何两个集合的基数是可比较的，每个非平凡的单位环都有一个极大理想，每个向量空间都有基，每个连通图都有一个生成树，每个紧空间的积是紧的，等等。选择公理常常允许将定理推广到 “更大的” 对象。例如，可以在没有选择公理的情况下证明每个有限维向量空间都有基，但推广到所有向量空间则需要选择公理。同样，有限个紧空间的积可以在没有选择公理的情况下证明是紧的，但推广到无限积（提霍诺夫定理）则需要选择公理。

　　 独立性结果的证明还表明，一个广泛的数学命题类，包括所有可以用皮亚诺算术语言表达的命题，可以在 ZF 中证明当且仅当它们在 ZFC 中也能证明。\(^\text{[20]}\) 这个类中的命题包括 \(P = NP\) 的命题、黎曼假设以及许多其他未解决的数学问题。在尝试解决这一类问题时，如果唯一的问题是证明的存在，那么使用 ZF 还是 ZFC 并没有区别。然而，从 ZFC 出发，可能会有比从 ZF 更简短的证明。

　　 选择公理不是唯一一个与 ZF 无关的重要命题。例如，广义连续统假设（GCH）不仅与 ZF 无关，而且与 ZFC 无关。然而，ZF 加 GCH 蕴含 AC，使得 GCH 比 AC 更强，即便它们都与 ZF 无关。

7. 更强的公理

　　 构造性公理和广义连续统假设各自暗示选择公理，因此它们比选择公理更强。在像冯·诺伊曼–伯纳耶–哥德尔集合论和莫尔斯–凯利集合论这样的类理论中，有一个叫做全局选择公理的公理，它比选择公理更强，因为它也适用于适当类。全局选择公理可以从大小限制公理推导出来。塔尔斯基公理，用于塔尔斯基–格罗滕迪克集合论中，表示（通俗地说）每个集合属于某个格罗滕迪克宇宙，它比选择公理更强。

8. 等价性

　　 有一些重要的命题，在假设 ZF 公理但不假设选择公理（AC）或选择公理的否定（¬AC）时，它们与选择公理等价。\(^\text{[21]}\) 其中最重要的包括佐恩引理和良序定理。实际上，泽梅洛最初引入选择公理是为了形式化他对良序定理的证明。

范畴论

　　 在范畴论中，一些结果在其证明中需要使用选择公理。这些结果相对于选择公理的强弱关系，取决于所采用技术基础的强度。举例来说，如果将范畴定义为集合，即对象和态射构成的集合（通常称为 “小范畴”），那么就不存在 “所有集合构成的范畴”，因此很难将范畴论的表述应用于所有集合。另一方面，其他更强的范畴论基础描述（如类论）可能显著更强，此时对选择公理的同样范畴论表述可能比标准形式更强。

　　 需要选择公理的范畴论命题示例包括：

9. 较弱形式

　　 有几个较弱的命题，它们与选择公理密切相关，但并不等价。一个例子是依赖选择公理（DC）。一个更弱的例子是可数选择公理（ACω 或 CC），它表明对于任何可数个非空集合，存在一个选择函数。这些公理足以支持许多初等数学分析中的证明，并且与一些原则是一致的，例如所有实数集合的勒贝格可测性，这些原则无法从完全的选择公理中推导出来。

　　 给定一个序数参数 \(\alpha \geq \omega + 2\)—— 对于每个秩小于 \(\alpha\) 的集合 \(S\)，\(S\) 是良序的。给定一个序数参数 \(\alpha \geq 1\)—— 对于每个哈托格数小于 \(\omega^\alpha\) 的集合 \(S\)，\(S\) 是良序的。随着序数参数的增加，这些命题越来越接近完全的选择公理。

　　 其他比选择公理更弱的选择公理包括布尔素理想定理和统一化公理。前者在 ZF 中与塔尔斯基的 1930 年超滤子引理等价：每个滤子都是某个超滤子的子集。

需要选择公理（或较弱形式）但比选择公理更弱的结果

　　 选择公理最有趣的方面之一是它在数学中的广泛应用。以下是一些需要选择公理的命题，这些命题在 ZF 中无法证明，但在 ZFC（ZF 加上选择公理）中可以证明。等价地，这些命题在所有 ZFC 模型中为真，但在某些 ZF 模型中为假。

可能等价的选择公理推论

　　 有几个历史上重要的集合论命题，它们由选择公理（AC）推导出来，但与选择公理是否等价仍然是一个悬而未解的问题。泽梅洛提到了划分原则（Partition Principle，PP），该原则在选择公理提出之前就已被表述，并且作为支持选择公理的理由。1906 年，罗素宣称划分原则与选择公理等价，但划分原则是否暗示选择公理仍然是集合论中最古老的未解问题之一，\(^\text{[35]}\) 其他命题的等价性也是类似的困难的开放问题。在每个已知的选择公理失败的 ZF 模型中，这些命题也都失败，但是否可以在没有选择公理的情况下成立仍然未知。

10. 选择公理否定的更强形式

　　 如果我们用 BP 来缩写 “每个实数集合具有贝尔性质” 的命题，那么 BP 比 ¬AC 更强，后者断言可能仅对一个非空集合族不存在任何选择函数。加强的否定可能与选择公理的弱化形式兼容。例如，ZF + DC\(^\text{[36]}\) + BP 是一致的，如果 ZF 本身是一致的。

　　 ZF + DC 与每个实数集合都是勒贝格可测的这一命题也是一致的，但这个一致性结果，由 Robert M. Solovay 提出，无法在 ZFC 本身中证明，而需要一个温和的大基数假设（存在一个不可达基数）。更强的决定性公理（AD）暗示每个实数集合都是勒贝格可测的，具有贝尔性质，并具有完美集性质（这三个结果都被选择公理本身反驳）。ZF + DC + AD 是一致的，前提是存在一个足够强的大基数公理是一致的（即存在无限多个 Woodin 基数）。

　　 奎因的公理化集合论系统《新基础》（得名于其 1937 年文章《数学逻辑的新基础》（"New Foundations for Mathematical Logic"）的标题。在 NF 公理系统中，选择公理可以被否定。\(^\text{[37]}\)

11. 暗示选择公理否定的命题

　　 存在一些泽梅洛-弗兰克尔集合论的模型，在这些模型中选择公理是错误的。我们将 “泽梅洛-弗兰克尔集合论加上选择公理的否定” 缩写为 ZF¬C。在某些 ZF¬C 模型中，有可能验证一些标准 ZFC 定理的否定。由于任何 ZF¬C 模型也是 ZF 模型，因此对于以下每个命题，存在一个 ZF 模型，其中该命题为真。

　　 有关证明，请参见 Jech（2008）。

　　 此外，通过对集合施加可定义性条件（在描述集合论的意义上），通常可以从与一般选择公理不兼容的公理中证明选择公理的限制版本。例如，这在 Moschovakis 编码引理中出现。

12. 类型理论中的选择公理

　　 在类型理论中，有一种不同的命题被称为选择公理。这个形式从两个类型 \(\sigma\) 和 \(\tau\) 开始，并且给定一个类型 \(\sigma\) 的对象与类型 \(\tau\) 的对象之间的关系 \(R\)。选择公理声明，如果对于每个类型为 \(\sigma\) 的 \(x\)，存在一个类型为 \(\tau\) 的 \(y\)，使得 \(R(x,y)\) 成立，那么存在一个从类型 \(\sigma\) 的对象到类型 \(\tau\) 的对象的函数 \(f\)，使得对于所有类型为 \(\sigma\) 的 \(x\)，都有 \(R(x,f(x))\) 成立： \[ (\forall x^{\sigma})(\exists y^{\tau})R(x,y) \to (\exists f^{\sigma \to \tau})(\forall x^{\sigma})R(x,f(x)).~ \] 与集合论不同，类型理论中的选择公理通常作为公理方案表述，其中 \(R\) 可以是所有公式的变体，或者是某种特定逻辑形式的所有公式的变体。

13. 注释

  1. 策梅洛 1904.
  2. 约翰·贝尔（2021 年 12 月 10 日）。"选择公理"。《斯坦福哲学百科全书》。检索于 2024 年 12 月 2 日。让我们将策梅洛 1908 年的表述称为**组合选择公理（CAC）： CAC：任何由互不相交的非空集合构成的集合族均存在一个横截集。
  3. 耶赫 1977, 第 351 页
  4. 耶赫 1977, 第 348 页及后续；马丁-洛夫 2008, 第 210 页。 根据门德尔松 1964, 第 201 页： > "近年来，选择公理的地位已不再那么具有争议性。对大多数数学家而言，它似乎非常合理，并且在几乎所有数学分支中都有重要应用，以至于不接受它就像是对实践数学家的一种故意束缚。"
  5. 史蒂文·罗森伯格（2021 年 12 月 21 日）。《抽象代数导论》。CRC 出版社。ISBN 9781000516333.
  6. 赫利希 2006, 第 9 页。 根据萨佩斯 1972, 第 243 页，这是策梅洛 1904 年最初提出的选择公理表述形式。另见哈尔莫斯 1960, 第 60 页对此形式的讨论。
  7. 萨佩斯 1972, 第 240 页。
  8. 图拉基斯（2003），第 209–210 页，第 215–216 页。
  9. 弗兰克尔、亚伯拉罕·A.；巴-希勒尔、耶霍舒亚；莱维、阿兹列尔（1973），《集合论基础》（第二版），阿姆斯特丹-伦敦：北荷兰出版公司，第 69–70 页，ISBN 9780080887050，MR 0345816。
  10. 保罗·C·罗森布鲁姆（2005），《数理逻辑要素》，多佛出版社，第 147 页，ISBN 9780486446172。
  11. 道森，J. W.（2006 年 8 月），《根基动摇抑或开创性重构？对库尔特·哥德尔在逻辑学、数学与计算机科学中影响的百年评估》，载于《第 21 届 IEEE 计算机科学逻辑年度研讨会论文集（LICS 2006）》，第 339–341 页，doi:10.1109/LICS.2006.47，ISBN 978-0-7695-2631-7，S2CID 15526447。 > "选择公理虽在分析的许多论证中被无意识地使用，但其一旦被明确化便引发争议，不仅因其非构造性特征，更因其导致诸如巴拿赫-塔斯基悖论等极度反直觉的结论。"
  12. 佩尔·马丁-洛夫，《直觉主义类型论》，1980 年。 安妮·斯耶普·特鲁尔斯特拉，《直觉主义算术与分析的元数学研究》，Springer 出版社，1973 年。
  13. 马丁-洛夫，佩尔（2006），《策梅洛选择公理百年：问题何在？》，《计算机期刊》第 49 卷第 3 期，第 345–350 页。Bibcode:1980CompJ..23..262L，doi:10.1093/comjnl/bxh162。
  14. 埃雷特·毕晓普与道格拉斯·S·布里奇斯，《构造性分析》，Springer-Verlag 出版社，1985 年。
  15. 弗雷德·里奇曼，《无选择公理的构造性数学》，载于《重聚对跖点——连续统的构造性与非标准观点》（P. Schuster 等编），《综合文库》第 306 卷，第 199–205 页，Kluwer 学术出版社，阿姆斯特丹，2001 年。
  16. Fraenkel 1922.
  17. Mostowski 1938.
  18. Gödel, Kurt (1938 年 11 月 9 日)。"选择公理和广义连续统假设的一致性"。《美国国家科学院院刊》，24（12）：556-557。Bibcode:1938PNAS...24..556G。doi:10.1073/pnas.24.12.556。PMC 1077160。PMID 16577857。
  19. 科恩，保罗（2019）。《选择公理的独立性》（PDF）。斯坦福大学图书馆。存档(PDF)于 2022 年 10 月 9 日的原始版本。检索于 2019 年 3 月 22 日。
  20. 这是由于算术命题相对于可构造宇宙 L 是绝对的。Shoenfield 绝对性定理给出了更一般性的结论。
  21. 关于 74 个等价命题的结构化列表，参见 Moore 2013 年第 330–334 页。关于 86 个带原始文献引用的等价命题，参见 Howard & Rubin 1998 年第 11–16 页。
  22. 布拉斯，安德烈亚斯（1984）。《基的存在性蕴含选择公理》。公理集合论（美国科罗拉多州博尔德，1983 年）。当代数学丛书（第 31 卷）。罗德岛州普罗维登斯：美国数学学会。第 31–33 页。doi:10.1090/conm/031/763890。ISBN 978-0-8218-5026-8。MR 0763890。
  23. A. Hajnal, A. Kertész: 一些选择公理的新代数等价，数学出版物 Debrecen, 19(1972)，339-340，另见 H. Rubin, J. Rubin, 选择公理的等价物，II，北荷兰出版社，1985 年，第 111 页。
  24. Blass, Andreas (1979)。“单射性、投影性与选择公理”。美国数学学会会刊，255: 31-59。doi:10.2307/1998165。JSTOR 1998165。
  25. Awodey, Steve (2010). 《范畴论》（第二版）。牛津：牛津大学出版社。第 20–24 页。ISBN 978-0199237180。OCLC 740446073。
  26. nLab 上的投影对象
  27. Serre, Jean-Pierre (2003)，《树》，Springer 数学丛书，Springer，第 23 页；Soukup, Lajos (2008)，“无限组合学：从有限到无限”，《组合学的视野》，Bolyai 数学研究丛书，第 17 卷，柏林：Springer，第 189–213 页，CiteSeerX 10.1.1.222.5699，doi:10.1007/978-3-540-77200-2_10，ISBN 978-3-540-77199-9，MR 2432534。特别见定理 2.1，第 192–193 页。
  28. Muger, Michael (2020). 《实用数学家的拓扑学》。
  29. Jech (2008)，第 119–131 页，证明了可数选择公理蕴含无限集与 Dedekind 无限集的等价关系，但无限集与 Dedekind 无限集的等价关系并不蕴含 ZF 中的可数选择公理。
  30. Lévy (1958)及其他人利用 Mostowski 模型证明了在没有选择公理（AC）的 ZF 中，关于有限集的八种定义是独立的，尽管在假设选择公理时它们是等价的。这些定义分别是 I-有限、Ia-有限、II-有限、III-有限、IV-有限、V-有限、VI-有限和 VII-有限。I-有限性与普通有限性相同。IV-有限性与 Dedekind 有限性相同。
  31. Sageev, Gershon (1975 年 3 月)。“关于选择公理的独立性结果”。《数学逻辑年刊》，8 (1–2)：1–184。doi:10.1016/0003-4843(75)90002-9。
  32. "[FOM] Are (C,+) and (R,+) isomorphic". 2006 年 2 月 21 日。
  33. Ash, C. J. (1975)。“选择公理的一个后果”。《澳大利亚数学学会学报》，19 (3)：306–308。doi:10.1017/S1446788700031505。S2CID 122334025。
  34. Schechter 1996，第 391–392 页。
  35. “关于分割原理”。
  36. 依赖选择公理
  37. “奎因的新基础”。《斯坦福哲学百科全书》。检索于 2017 年 11 月 10 日。
  38. Jech 2008，第 142–144 页，定理 10.6 及证明。
  39. Stavi, Jonathan (1974)。“一个具有无限自由完备布尔代数的 ZF 模型”。《以色列数学学报》，20 (2)：149–163。doi:10.1007/BF02757883。S2CID 119543439。

14. 参考文献

　　 翻译收录于：Jean van Heijenoort, 2002 年。《从弗雷格到哥德尔：数学逻辑的源书，1879–1931》。新版本。哈佛大学出版社。ISBN 0-674-32449-8

15. 外部链接


致读者： 小时百科一直以来坚持所有内容免费无广告，这导致我们处于严重的亏损状态。 长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。 因此，我们请求广大读者热心打赏 ，使网站得以健康发展。 如果看到这条信息的每位读者能慷慨打赏 20 元，我们一周就能脱离亏损， 并在接下来的一年里向所有读者继续免费提供优质内容。 但遗憾的是只有不到 1% 的读者愿意捐款， 他们的付出帮助了 99% 的读者免费获取知识， 我们在此表示感谢。

                     

友情链接： 超理论坛　|　©小时科技 保留一切权利