贡献者: _Eden_
假如两种原子交替排布构成了一维双原子链,一共 $N$ 个原胞,每个原胞有 $P,Q$ 两个原子。加入只考虑相邻原子间的相互作用,设相邻两原子间的相互作用能为
\begin{equation}
V(a+\delta)=V(a)+\frac{1}{2}\beta \delta^2+\text{高阶项}~.
\end{equation}
,则相邻原子间作用力为
\begin{equation}
F=-\frac{ \,\mathrm{d}{V} }{ \,\mathrm{d}{\delta} }=-\beta \delta~.
\end{equation}
设 $P,Q$ 两原子的质量分别为 $m,M$,并设平衡状态下相邻两原子间距离为 $a$,那么可以列出牛顿方程:
\begin{equation}
\begin{aligned}
&m\ddot \mu_{2n}=\beta(\mu_{2n+1}+\mu_{2n-1}-2\mu_{2n})~,\\
&M\ddot \mu_{2n+1}=\beta(\mu_{2n+2}+\mu_{2n}-2\mu_{2n+1})~.
\end{aligned}
\end{equation}
1. 格波解与色散关系
仿照一维单原子链晶格的方法,我们设双原子链晶格也有格波形式的解
\begin{equation}
\mu_{2n}=A e^{i(\omega t - 2naq)},\mu_{2n+1}=B e^{i(\omega t - (2n+1)aq)}~.
\end{equation}
注意 $A,B$ 可以是复数,而最终 $\mu_{2n}$ 和 $\mu_{2n+1}$ 的可观测部分只有实部。代入
式 3 后可以得到
\begin{equation}
\begin{aligned}
&(m\omega^2-2\beta)A+2\beta \cos\left(aq\right) B=0~,\\
&2\beta \cos\left(aq\right) A+(M\omega^2-2\beta)B=0~.
\end{aligned}
\end{equation}
因此如果把 $A,B$ 看作未知量,方程存在解的条件是系数矩阵的行列式为 $0$,即
\begin{equation}
\left|
\begin{matrix}
m\omega^2-2\beta&2\beta \cos\left(aq\right) \\
2\beta \cos\left(aq\right) &M\omega^2-2\beta
\end{matrix}
\right|=0~.
\end{equation}
因此,任意波数 $q$,都对应两种可能的频率值
\begin{equation}
\omega_{\pm}^2=\beta\frac{m+M}{mM} \left\{1\pm \left[1-\frac{4mM}{(m+M)^2}\sin^2(aq) \right] ^2 \right\} ~.
\end{equation}
代回
式 5 ,可以求得 $P,Q$ 两原子振幅之比:
\begin{equation}
\left(\frac{B}{A} \right) _{\pm}=-\frac{m\omega_{\pm}^2-2\beta}{2\beta \cos\left(aq\right) }~,
\end{equation}
现在我们要对有一定大小的晶格进行分析。一共 $N$ 个原胞,其中最左边的原子和最右边的原子位于晶格的边界处不好处理。所以我们采用周期性边界条件(玻恩-卡曼条件),假设这个原子链的头部 $P$ 原子和尾部 $Q$ 原子相连,形成一个环。这样的话所有原子满足的方程仍然是式 3 ,唯一的限制条件是 式 4 种 $\mu_{m}=\mu_{m+2N}$。所以 $q$ 不再是连续的,而是离散的:
\begin{equation}
q=\frac{2\pi}{2Na} \cdot n~.
\end{equation}
不难发现 $q$ 的格波解可以用 $q+\pi/a$ 的格波解形式来表示,因此布里渊区大小为 $\pi/a$(并且和上面的讨论类似地,一个 $q$ 可以解得两种不同的 $\omega$,对应两个不同的 $A,B$ 组合,对应两个不同的格波解)。注意到在一维单原子链晶格中 $q$ 和 $q+2\pi/a$ 是等价的,布里渊区大小为 $2\pi/a$,而在此处我们双原子链晶格采取 $\pi/a$,这是因为此处我们讨论的双原子链晶格的原胞大小为 $2a$。
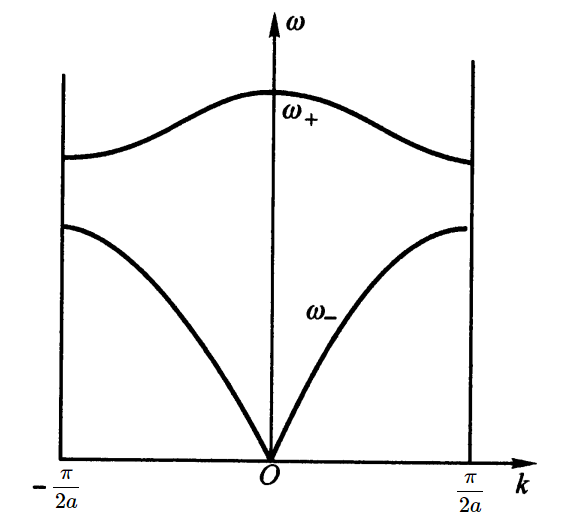
2. 声学支和光学支
将色散曲线在简约布里渊区中画出,将观察到上下两条曲线。其中下方的曲线当 $ \boldsymbol{\mathbf{k}} =0$ 时 $\omega=0$,它也被称为声学支,当 $\omega/k$ 近似为常数时,$\omega/k$ 为晶格中声子的速度,即振动传播的速度。
声学支代表原胞内两个原子同向地运动,即式 8 中 $B$ 与 $A$ 的符号相同。
图 1:声学支和光学支
如图所示,上方的色散曲线被称为光学支。注意到直线 $\omega=ck$ 与这条曲线有交点,而交点的位置大致在 $k=0,\omega_{\max}=\omega_+(0)$ 附近。这意味着,这种振动模式能被电磁波激发。这种振动模式的特点是,同一个原胞内的两个原子振动方向相反,$B$ 与 $A$ 的符号相反。由于 $A$ 和 $B$ 是两个不同的原子,所以它们在作相对振动的时候,等效于一个不停振荡的电偶极矩,所以与同频率的电磁波具有很强的相互作用。在实际的离子晶体中也存在强烈的远红外吸收现象,其原理是一致的。而如果晶体是非极化的,例如 $A,B$ 是同一种原子,则它们作相对振动时不会产生振荡的偶极矩,也就不会产生红外吸收现象。
三维的复式晶格,并且假设每个原胞内有 $n$ 个原子,则情况会比较复杂,但我们可以先考虑 $k\rightarrow 0$,即波长 $\lambda\rightarrow \infty$ 时的情况。此时 $\lambda\gg a$,晶格常数远小于波长,导致晶体振动可以看作是连续介质的振动,因此沿 $ \boldsymbol{\mathbf{k}} $ 方向的声波具有 $3$ 个自由度:一个是纵波,另外两个是横波。将 $ \boldsymbol{\mathbf{k}} $ 方向的色散曲线画出,将发现有 $3$ 条声学支,其余 $3n-3$ 条是光学支。$k=0$ 附近声学支的斜率对应于长波近似下声波的速度。