坐标定轴旋转程序(Matlab)
贡献者: addis
这里给出一个 Matlab 函数 turn() 可以一次把三维空间中若干点绕非零矢量 $ \boldsymbol{\mathbf{A}} $ 按照右手定则旋转角度 $\theta$。在程序中,这些点可以用任意形状的 X, Y, Z 数组来表示,也可以用单个三列的矩阵 $P$ 来表示(每列分别为 $x, y, z$ 坐标)。$ \boldsymbol{\mathbf{A}} $ 和 $\theta$ 既可以直接指定,也可以通过指定两个矢量 $ \boldsymbol{\mathbf{D}} _1, \boldsymbol{\mathbf{D}} _2$:$ \boldsymbol{\mathbf{A}} $ 垂直于 $ \boldsymbol{\mathbf{D}} _1, \boldsymbol{\mathbf{D}} _2$,且把 $ \boldsymbol{\mathbf{D}} _1$ 方向转到 $ \boldsymbol{\mathbf{D}} _2$ 方向。
使用示例:转动一个正方形
图 1:运行结果 1:绕 $z$ 轴转动
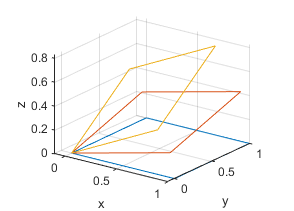
图 2:运行结果 2:绕 $(1,-1,0)$ 轴转动
代码 1:turn_demo.m
% turn_demo
A = [1,-1,0]; % [0, 0, 1]
X = [0,1,1,0,0]; Y = [0,0,1,1,0]; Z = [0,0,0,0,0];
figure; plot3(X, Y, Z);
grid on; hold on; axis equal;
xlabel x; ylabel y; zlabel z;
view(36,20);
[X1,Y1,Z1] = turn(X,Y,Z,A,pi/10);
[X2,Y2,Z2] = turn(X,Y,Z,A,pi/5);
plot3(X1, Y1, Z1);
plot3(X2, Y2, Z2);
代码 2:turn.m
% 格式 0
% [X1,Y1,Z1] = turn(X,Y,Z,A,theta) 把空间点绕原点以 A 方向为轴逆时针转动theta角
% [X1,Y1,Z1] = turn(X,Y,Z,D1,D2) 把空间点由 D1 方向绕原点转到 D2 方向
% numel(X) = numel(Y) = numel(Z)
% numel(D1) = numel(D2) = numel(A) = 3
% numel(theta) = 1
% 格式 1
% P1 = turn(P,A,theta) 把空间点绕原点以 A 方向为轴逆时针转动 theta 角
% P1 = turn(P,D1,D2) 把空间点由 D1 方向绕原点转到 D2 方向
% P, P1 的每行是一个点, size(P) = size(P1) = [N,3]
function [X1, Y1, Z1] = turn(X, Y, Z, A, theta)
% 格式检查
flag = 0; % flag = 0 表示格式 0, flag = 1 表示格式 1
if nargout == 1 && nargin == 3 % 格式检查
A = Y; theta = Z;
Y = X(:,2); Z = X(:,3); X = X(:,1);
flag = 1;
elseif numel(X) ~= numel(Y) || numel(Y) ~= numel(Z) %格式 0 要求 xyz 元素个数相同即可
error('numel of x, y, z is not equal')
end
if length(A(:)) ~= 3 % 两种格式都要求 A 是一个矢量
error('length A is not 3');
end
if numel(theta) == 3
D1 = A/norm(A);
D2 = theta/norm(theta);
A = cross(D1,D2);
C = dot(D1,D2);
S = sqrt(1-C^2);
elseif numel(theta) == 1
C = cos(theta);
S = sin(theta);
else
error('numel(theta)~=1 or numel(A2)~=3');
end
normA = sqrt(A(1)^2 + A(2)^2 + A(3)^2);
if normA == 0
X1 = X; Y1 = Y; Z1 = Z;
return;
end
A0 = A / normA;
Ax = A0(1); Ay = A0(2); Az = A0(3);
C1 = 1 - C;
M = ... % 见 https://wuli.wiki/changed/RotA.html
[
C1*Ax*Ax+C C1*Ax*Ay-Az*S C1*Ax*Az+Ay*S
C1*Ay*Ax+Az*S C1*Ay*Ay+C C1*Ay*Az-Ax*S
C1*Az*Ax-Ay*S C1*Az*Ay+Ax*S C1*Az*Az+C
];
XYZ1 = M*[X(:)';Y(:)';Z(:)'];
if flag == 0 % 原格式
X1 = zeros(size(X));
Y1 = zeros(size(Y));
Z1 = zeros(size(Z));
X1(:)=XYZ1(1,:);
Y1(:)=XYZ1(2,:);
Z1(:)=XYZ1(3,:);
else % 新格式
X1 = XYZ1';
Y1 = []; Z1 = [];
end
end