cos2 波包

贡献者： addis

1. cos2 波包

　　 $\cos^2$ 波包也叫 $\sin^2$ 波包，比起高斯波包，它的优点是存在明确的范围。它的函数形式为

\begin{equation} f(x) = \left\{\begin{aligned} &A\cos^2 \left(\frac{\pi x}{L} \right) \mathrm{e} ^{ \mathrm{i} k x} && ( \left\lvert x \right\rvert < L/2)\\ &0 && (\text{otherwise})~. \end{aligned}\right. \end{equation}

其中 $L$ 是波包的总长度。它的 FWHMI 为

\begin{equation} \text{FWHMI} = \frac{2}{\pi} \operatorname {acos}(2^{-1/4}) L \approx 0.3640567 L~. \end{equation}

满足 $f^2(\text{FWHMI/2}) = f^2(0)/2$。

　　积分为（令 $a = \pi/L$）

\begin{equation} \begin{aligned} &\quad \int A\cos^2 \left(a x \right) \mathrm{e} ^{ \mathrm{i} kx} \,\mathrm{d}{x} = - \mathrm{i} \frac{A}{4} \mathrm{e} ^{ \mathrm{i} kx} \left(\frac{2}{k} +\frac{ \mathrm{e} ^{2 \mathrm{i} ax}}{2a+k} -\frac{ \mathrm{e} ^{-2 \mathrm{i} ax}}{2a-k} \right) + \frac{2 \mathrm{i} Aa^2\cos[{\pi k}/{(2a)}]}{k(4 a^2 -k^2)} + C\\ &= \frac{Ax}{4} \left(2 \operatorname{sinc} (k x) + \operatorname{sinc} [(2 a+k)x] + \operatorname{sinc} [(2 a-k)x] \right) \\ &\quad + \mathrm{i} \frac{A}{4} \left(-\frac{2 \cos\left(k x\right) }{k} -\frac{\cos[(2 a+k)x]}{2 a+k} +\frac{\cos[(2 a-k)x]}{2 a-k} \right) + \frac{2 \mathrm{i} Aa^2\cos[{\pi k}/{(2a)}]}{k(4 a^2 -k^2)} + C~. \end{aligned} \end{equation}

$C$ 前面的部分在 $x = \pm\pi/(2a)$ 处分别为 $\frac{\pm 2 Aa^2\sin[{\pi k}/{(2a)}]}{k(4 a^2 -k^2)}$，易得无穷定积分只有实部

\begin{equation}\int_{-\infty}^{+\infty} f(x) \,\mathrm{d}{x} = \int_{-\pi/(2a)}^{\pi/(2a)} A\cos^2 \left(a x \right) \mathrm{e} ^{ \mathrm{i} k x} \,\mathrm{d}{x} = \frac{4 Aa^2\sin[{\pi k}/{(2a)}]}{k(4 a^2 -k^2)}~. \end{equation}

另外，实部是奇函数，虚部是偶函数。

　　傅里叶变换（注意是实数）：

\begin{equation} \tilde f(k) = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{+\infty} f(x) \mathrm{e} ^{- \mathrm{i} \omega x} \,\mathrm{d}{x} = \frac{\sqrt{2} \pi ^{3/2} A L}{4 \pi ^2-L^2 (\omega-k)^2} \operatorname{sinc} [L(\omega-k)/2]~. \end{equation}

零点的位置为

\begin{equation} k = k_0 \pm 2n\pi/L \qquad (n=2,3,\dots)~. \end{equation}

标准差约为 $2.92544/L$，方差 $13.15947/L^2$，FWHMI $9.05144/L$。

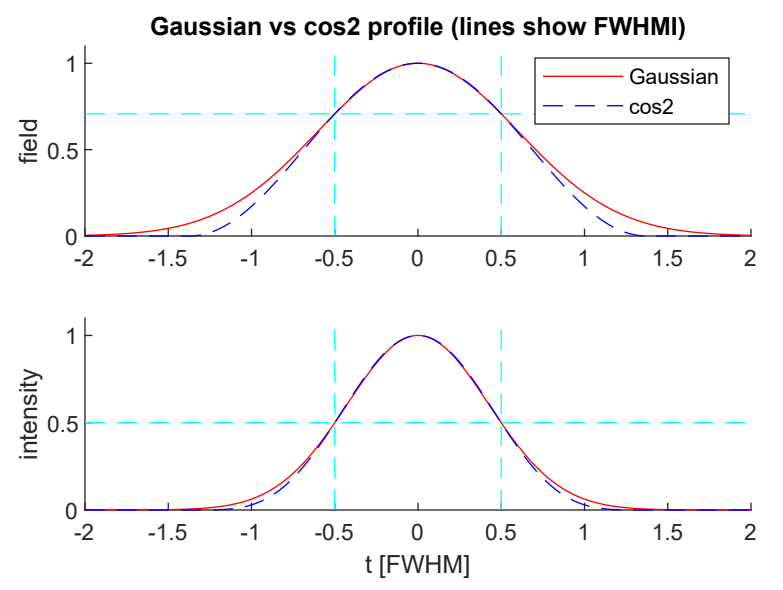
　　画图对比如下（代码见文末）：

图 1：高斯波包和 cos2 波包的对比

2. 附：Matlab 画图代码

代码 1：cos2_spec.m

% properties of cos2 wave packet spectra

A = 0.9; L = 1.12;
g = @(k) (sqrt(2)*pi^1.5*A*L)./(4*pi^2-L^2*k.^2) .* sinc(L*k/2);

k = linspace(-40, 40, 1000);
figure; plot(k, g(k));
grid on;
xlabel k;
hold on;
scatter((2:6)*2*pi/L, 0, 'k');
scatter((-6:-2)*2*pi/L, 0, 'k');
axis([-40, 40, -0.02, 0.21]);

A = 1/sqrt(integral(@(k)g(k).^2, -inf, inf));
integral(@(k)g(k).^2.*abs(k).*A^2, -inf, inf)

代码 2：FWHMIsin2

% FWHMI of wave packets
% FWHMI: full width half maximum intensity
% return the ratio of FWHMI of sin2 (field) wave v.s. total duration
% satisfy: |cos(pi/2 * FWHMIsin2)^2|^2 == 1/2

function ret = FWHMIsin2
    ret = 2*acos(2^(-1/4))/pi;
end

代码 3：cos2_gaussian_compare.m

% plot Gaussian vs cos2 profile

% gaussian
FWHMI = 1;
a = iFWHMIexp(FWHMI);
x = linspace(-2*FWHMI, 2*FWHMI, 1000);
field_gauss = exp(-a.*x.^2);

% cos2
field_cos2  = zeros(size(x));
dur_cos2 = FWHMI / FWHMIsin2;
mark = abs(x) < dur_cos2/2;
field_cos2(mark) = cos((pi/2)*x(mark)/(dur_cos2/2)).^2;

% plot field profile
figure;
subplot(2, 1, 1); hold on;
axis([min(x), max(x), 0, 1.1]);
plot_vert(-FWHMI/2, 'c--');
plot_vert(FWHMI/2, 'c--');
plot_hori(sqrt(1/2), 'c--');
plot(x, field_gauss, 'r');
plot(x, field_cos2, 'b--');
legend({'', '', '', 'Gaussian', 'cos2'});
% xlabel('t [FWHM]');
ylabel('field');
title('Gaussian vs cos2 profile (lines show FWHMI)');

% plot intensity profile
subplot(2, 1, 2); hold on;
axis([min(x), max(x), 0, 1.1]);
plot_vert(-FWHMI/2, 'c--');
plot_vert(FWHMI/2, 'c--');
plot_hori(1/2, 'c--');
plot(x, field_gauss.^2, 'r');
plot(x, field_cos2.^2, 'b--');
xlabel('t [FWHM]');
ylabel('intensity');