贡献者: FFjet; addis
用两个点波源作光的干涉实验的典型代表,是杨氏实验。
1. 实验装置
杨氏实验的装置如下图所示,
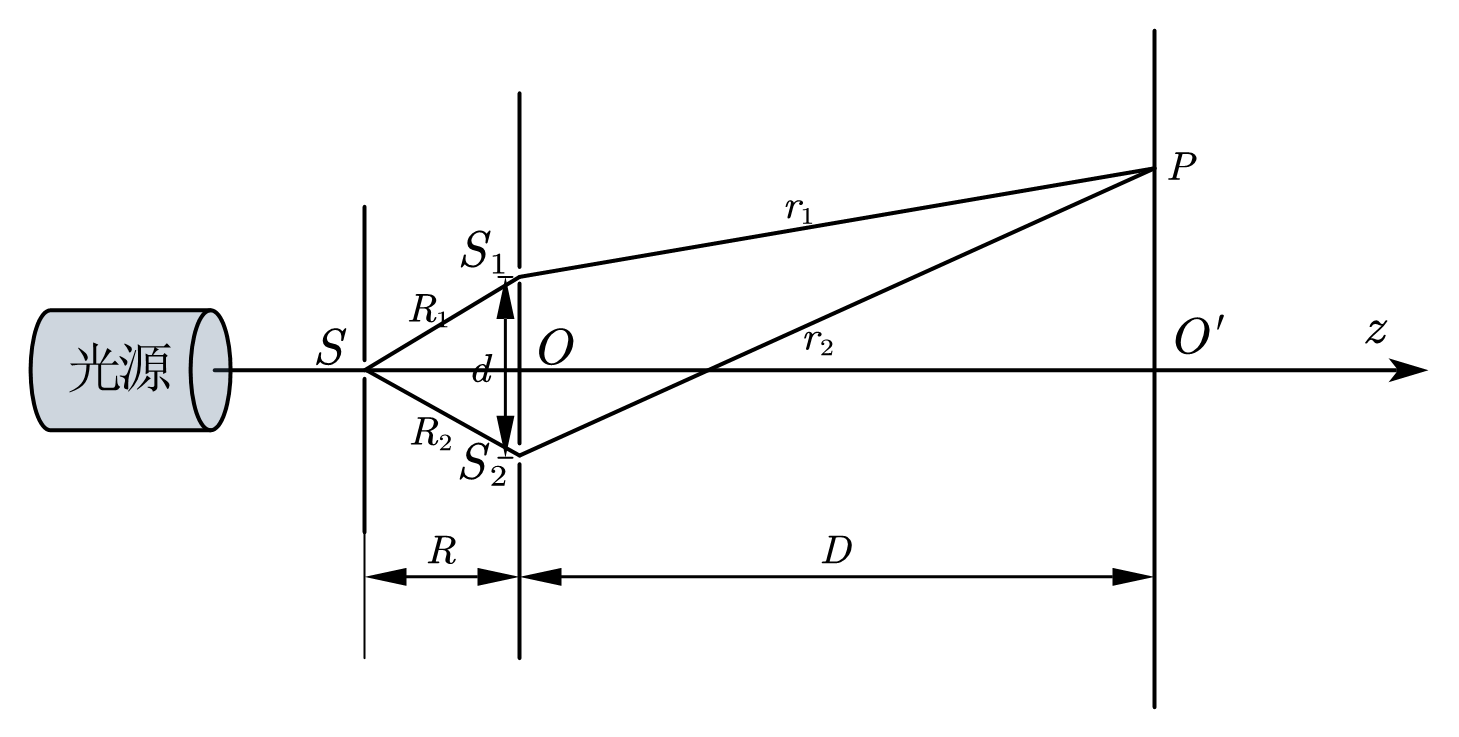
图 1:杨氏双缝干涉
在普通单色光源前面放一个开有小孔 $S$ 的屏,作为单色点光源。在 $S $ 的照明范围内再放一个开有两个小孔 $S_1,S_2$ 的屏。按惠更斯原理,$S$ 将作为两个次波源向前发射次波(球面波),形成交叠的波场。在较远的地方放置一接收屏,屏上可以观测到一组几乎是平行的直线条纹,如图 1 (b)。
但这样的亮度太低了。为了提高干涉条纹的亮度,实际中 $S,S_1,S_2$ 用三个互相平行的狭缝($S_1$ 和 $S_2$ 在同一竖直平面上并都与地面平行,$S$ 在一竖直平面上且与地面平行,且两竖直平面互相平行)
并且可不用屏幕接收,而代之以目镜直接观测。激光出现以后,人们可以用氦氖激光束直接照明双孔,在屏幕上即可获得一套相当明显的干涉条纹,供许多人同时观看。
2. 干涉明暗条纹的位置
现在来分析,用普通光源做杨氏实验时,由双孔出射的两束光波之间的相位差。设 $SS_1=R_1,SS_2=R_2$,用 $\varphi_0$ 代表点波源 $S$ 的初相位,则次波源 $S_1,S_2$ 的初相位分别为
\begin{equation}
\varphi_{10}=\varphi_{0}+\frac{2 \pi}{\lambda} R_{1}, \quad \varphi_{20}=\varphi_{0}+\frac{2 \pi}{\lambda} R_{2}~,
\end{equation}
从而
\begin{equation}
\varphi_{10}-\varphi_{20}=\frac{2 \pi}{\lambda}\left(R_{1}-R_{2}\right)~.
\end{equation}
由此可见,两次波之间的相位差与 $\varphi_0$ 无关,即使中 $\varphi_0$ 变了,相位差中 $\varphi_{10}-\varphi_{20}$ 也不变。下面来作一些计算。
令双孔间距为 $d$, 屏幕与双孔屏间的距离为 $D$,屏幕上横向观测范围为 $X$,我们设 $d^{2} \ll D^{2}$(这被称为远场条件),$X^{2} \ll D^{2}$(这被称为傍轴条件)。
设 $S_1$、$S_2$ 离 $S$ 的距离相等,即 $R_1=R_2$, 从而 $\varphi_{10}=\varphi_{20}$,为了简化运算,可以取二者皆为 $0$,不影响结论。如图 1 ,从线段 $S_1S_2$ 的中点 $O$ 作 $z$ 轴垂直于双孔屏和接收屏。设接收屏上点 $P$ 的横向距离为 $X$,$OP$ 与 $z$ 轴的夹角为 $\theta$。在远场条件下,可认为 $S_1P\parallel S_2P$,在傍轴条件下可认为 $OP$ 也与它们平行。从 $S_1$ 作 $OP$ 和 $S_2P$ 的垂线交 $S_2P$ 于 $N$。则 $\overline{S_2N}$ 近似等于光程差:
\begin{equation}
r_{1}-r_{2} \approx \overline{S_{2} N}=d \sin \theta \approx \frac{d x}{D}~,
\end{equation}
容易得到相位差
\begin{equation}
\delta(P)=\frac{2 \pi\left(r_{1}-r_{2}\right)}{\lambda}=\frac{2 \pi d}{\lambda D} x~.
\end{equation}
干涉条纹的形状,即等强度线是一组纵向(即与
图 1 垂直)的平行直线。强度随 $\delta(P)$ 作周期性变化。干涉条纹的间距定义为两条相邻亮纹(强度极大)或两条暗纹(强度极小)之间的距离。因为两条相邻条纹之间的光程差相差 $\lambda$,令
式 3 中 $r_1-r_2=\Delta L=\lambda$,$ x $ 写成条纹间隔 $\Delta x$,则有
\begin{equation}
\Delta x=\frac{\lambda D}{d}~.
\end{equation}
由上述分析可知,当 $P$ 点处为明纹时,有
\begin{equation}
x=\pm k \frac{D \lambda}{d} \quad k=0,1,2, \cdots~
\end{equation}
相应于 $k=0$ 的明纹称为
零级明纹或
中央明纹。相应于 $k=1, k=2, \cdots$ 的明纹,称为第一级、第二级、……明纹。
当 $P$ 点处为暗纹时,有
\begin{equation}
x=\pm(2 k+1) \frac{D \lambda}{2 d} \quad k=0,1,2, \cdots~
\end{equation}
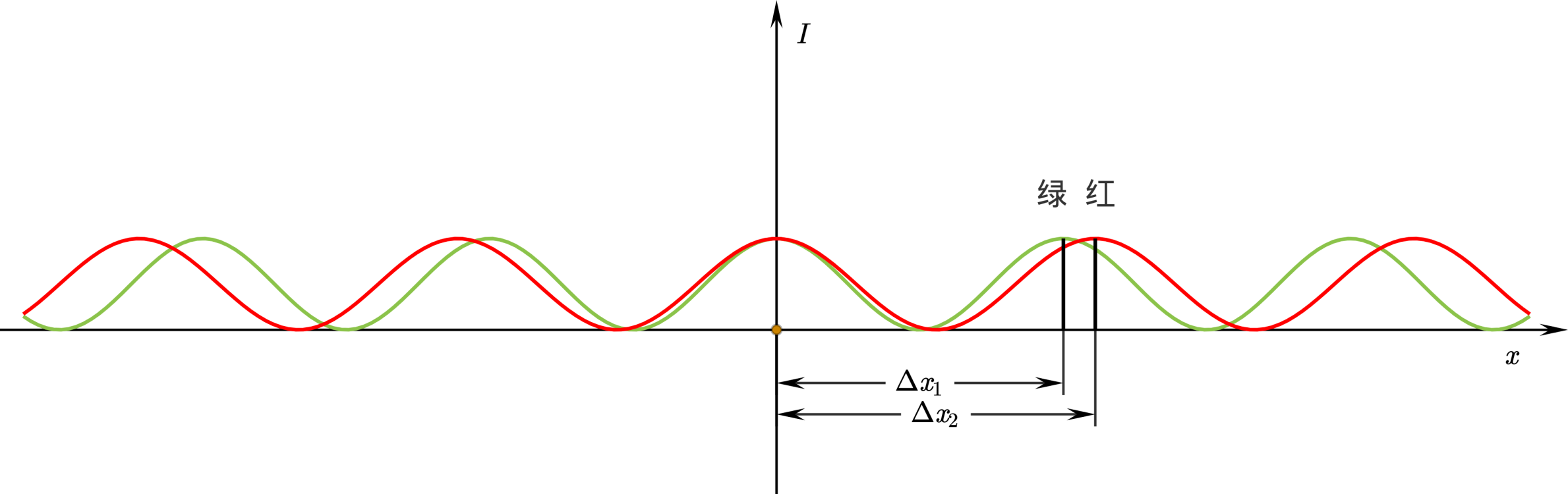
若光源中包含 $\lambda_1$ 和 $\lambda_2$ 两条谱线,则屏上有两套间距不等的条纹同时存在,它们非相干地叠加在一起,如图 2 所示。
图 2:两套不相同颜色干涉条纹不相干叠加
若光源发出的是白光,则在中央零级的白色亮纹两侧,对称地排列着若干条彩色条纹。
图 3:白光的杨氏双缝干涉图样(图片来自维基百科)