贡献者： addis; 叶月2_
电压（voltage） 是电势差的同义词，通常在讨论电路时使用，本文只讨论电路中的电压。电势差的定义为（式 8 ）
\begin{equation}
U_{21} = V( \boldsymbol{\mathbf{r}} _2) - V( \boldsymbol{\mathbf{r}} _1) = - \int_{ \boldsymbol{\mathbf{r}} _1}^{ \boldsymbol{\mathbf{r}} _2} \boldsymbol{\mathbf{E}} _0( \boldsymbol{\mathbf{r}} ) \boldsymbol\cdot \,\mathrm{d}{ \boldsymbol{\mathbf{r}} } ~.
\end{equation}
在 “
电势 电势能” 中，我们强调了要定义电荷的电势能或电势，我们必须要使用无旋的电场（保守场），而电路中一般来说既存在无旋场也存在有旋场（例如线圈的感生电场）。这时我们规定
式 1 中的 $ \boldsymbol{\mathbf{E}} _0( \boldsymbol{\mathbf{r}} )$
只包含电路中的净电荷产生的电场，也就是无旋的部分。
以下我们来举若干例子说明。第一个例子是电阻两端的电压，见 “电阻”。
再来看另一些例子
例 1 电容的电压
令平行板电容器两端分别有正负净电荷，我们知道在平行板之间会产生近似匀强的电场 $ \boldsymbol{\mathbf{E}} $，这个电场是电路中的净电荷产生的，所以需要计入式 1 。所以从带正电荷的平行板到带负电荷的平行板进行积分，结果为 $-E d$（$d$ 是平行板的距离）。所以带电容器带正电荷的一端的电势比另一端要高。
1. 电动势
例 2 化学电源
对于化学电源（即电池）两端产生的电压，我们应该如何通过上述的定义理解呢？这里介绍一个简单的模型。假设电池的两端构成一个平行板电容器（例 2 ），带正电荷的一端是电源的正极，带负电的一端是电源的负极，两个平行板之间存在导电材料，使电子可以在它们之间移动。
两极板之间存在从正极指向负极的匀强电场，使得它们之间的电子受到从负极到正极的电场力。所以如果电池中没有化学反应，电子将不断地从负极移动到正极，使得两极板的净电荷消失，电源两端电势差变为零。但若有化学反应，在这个模型中化学反应的作用相当于给每个电子施加一个与电场力等大反向的恒力，使得两极板间的电子合力为零，以保持两平行板上的净电荷不被中和。
当我们将电源接入电路开始工作时，负极的电子不断通过外电路移动到电源的正极，这时平行板之间的电场稍微变弱，电场力变得比化学反应提供的恒力略弱，电子就在这个恒力的作用下不断从平行板的正极移向负极，从而保持电源两端的电势差，产生源源不断的电流。
我们把非电场力对电荷作用后产生的电势差叫做电动势（electromotive force），化学电源的电动势只是一种，另一种常见的电动势是由电磁感应产生的。
由法拉第电磁感应定律可知，这部分电动势的表达式为：
\begin{equation}
\mathscr{E}=-\frac{\mathrm{d} \Phi}{\mathrm{d} t}=-\frac{\mathrm{d}}{\mathrm{d} t} \iint_{(S)} \boldsymbol{B} \cdot \mathrm{d} \boldsymbol{S}=-\frac{\mathrm{d}}{\mathrm{d} t} \oint_{(L)} \boldsymbol{A} \cdot \mathrm{d} \boldsymbol{l}=-\oint_{(L)} \frac{\partial \boldsymbol{A}}{\partial t} \cdot \mathrm{d} \boldsymbol{l}~.
\end{equation}
2. 感生电动势
例 3
假设我们有一个 $N$ 匝的不闭合线圈，两端接在理想电压表上。若线圈中存在变化的磁场，磁通量 $\Phi(t) = \alpha t$ 随时间线性增加，那么根据电磁感应我们知道电压表会显示稳定的读数 $\alpha$。
注意这并不是一个静电学问题，变化的磁场会沿着线圈产生涡旋电场，这是一个有旋场，所以在计算电路电压时我们不能将这部分电场算入（详见 “电势”）。
那为什么线圈两端还会产生电压呢？因为整个导线（忽略电阻）作为一个导体，其内部的总电场必须为零，所以当线圈放在涡旋电场中，线圈就会自动调整其净电荷分布，使线圈中处处存在与涡旋电场等大反向的，由净电荷产生的电场。而根据定义，这部分电场需要算入式 1 的积分中。由于线圈有 $N$ 匝，从导线的一端线积分到另一端，需要延导线一起环绕 $N$ 圈，所以线圈两端的电压（也叫感生电动势）与匝数成正比。
未完成：图未完成
由此我们可以看到，“导体内部电场为零/导体是等势体” 的说法和 “导线两端存在电压/电势差” 并不矛盾。前者指的是总电场，后者指的是总电场中的无旋部分的电势。
3. 动生电动势
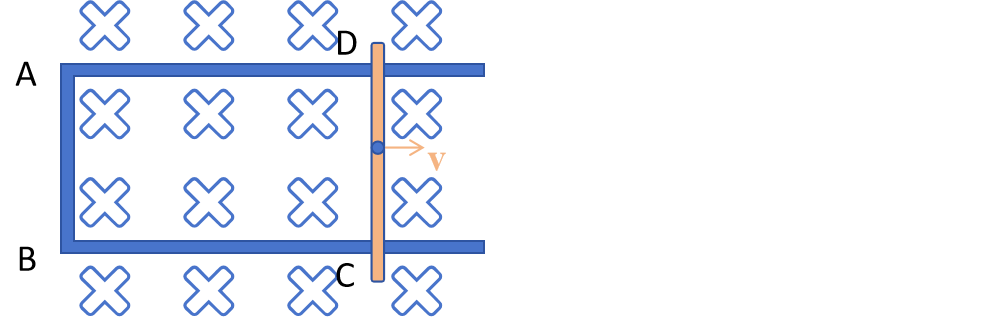
有时候，导体运动会导致磁通量发生变化，我们常把这部分贡献的电动势称为动生电动势。如下图所示，导体在磁场中向右运动，那么电子必定有向右的分速度，对应受到向下的洛伦兹力分力。在导体里，该洛伦兹力使得电子向下汇集，$D,C$ 端类似电源的正负极。
图 1：磁场中运动的导体棒
我们知道，电源的电动势为单位正电荷从负极到正极过程中非静电力所做的功。同理可得，对应于图 1 的动生电动势为：
\begin{equation}
\begin{aligned}
\mathscr{E}&=\int_{C}^D F\cdot d \boldsymbol{\mathbf{x}} \\
&=\int_{C}^{D} \boldsymbol{\mathbf{v}} \times \boldsymbol{\mathbf{B}} \mathrm{~d} \boldsymbol{\mathbf{x}} ~.
\end{aligned}
\end{equation}
图 1 是最简单的模型，但很多时候我们面对的不是这种横平竖直的导线结构，非静电力做功不一定是直线路径，因此
式 3 更为严谨的一种写法是线积分。
例 4
图 2：沿光滑斜轨道滑动的导体棒
假设一根导体棒在间距为 $L$ 的两个导体轨道上以速度 $v$ 匀速运动，导体电阻不计。空间中存在垂直于轨道平面向下的匀强磁场，大小为 $B$。求轨道之间的电压。
根据高中所学的洛伦兹力计算方法，导体中的电子将受到向右的洛伦兹力 $F = evB$，导体为了保持内部平衡（即电子受力为零），会在其表面重新分布净电荷，产生一个向左的静电场使得 $eE = evB$。所以轨道之间的电势差为 $U = EL = vBL$，且右端的电势高于左端。
注意该例不符合 “导体内部电场为零/导体是等势体”，因为存在磁场时这只对静止的导体适用。在学习 “电磁场的参考系变换” 后我们会发现如果我们将参考系与导体一起移动，在这个参考系中导体棒内部电场的确等于零。
