范德瓦尔斯气体

                     

贡献者： _Eden_

预备知识 1　理想气体，

　　 范德瓦尔斯方程是理想气体向真实气体的推广，架起了微观图像与宏观测量之间的桥梁。

　　 范德瓦尔斯对理想气体作了两点修正：1、真实气体占据一定体积；2、真实气体间有分子间作用势（Lennard-Jones 势是一个很好的近似）。范德瓦尔斯方程展现出惊人的威力——从它的图像上可以看出气液相变线，可以找到临界点……1910 年诺贝尔物理学奖授予范德瓦尔斯，以表彰他为气体和液体状态方程所作的工作。

1. 范式方程

　　 范德瓦尔斯方程可以写为

\begin{equation} \left(p+\frac{a}{V_m^2}\right)(V_m-b)=RT~. \end{equation}

　　 $b$ 是因为真实气体分子总占据一定体积而做的修正。$a$ 是考虑分子间作用力（主要是吸引力）而做的修正。这里只给出不严谨的分析计算，但给出的结果是与统计物理计算结果是一致的。

　　 设气体分子的有效直径为 $d$，分子原本能达到的空间体积为 $V_0=\frac{1}{6}\pi d^3$，当考虑它与另一分子的碰撞时，它所能达到的空间体积减少了 $\frac{4}{3}\pi d^3$。$1\rm mol$ 气体含有 $N_A$ 个气体分子，从一个粒子的角度看，它面对 $N_A-1$ 个排斥球，而每个排斥球只有一面可能对它产生排斥，体积只能算一半：

\begin{equation} b=\frac{1}{2}(N_A-1)(\frac{4}{3}\pi d^3)=4N_A V_0~. \end{equation}

　　 由于分子间作用力（主要是吸引力），碰撞容受到朝向容器内的吸引力而动量减小：所以要引入内压强 $\Delta p$。内压力正比于单位时间内碰撞器壁的粒子数，又正比于粒子数密度（影响吸引力的大小），所以 $\Delta p$ 正比于 $\frac{1}{V_m^2}$，所以设这个修正量为 $a/V_m^2$，$a$ 与相互作用势有关。设分子间作用力在 $r>d$ 时为林纳德琼斯势，当 $r\le d$ 时为钢球势（势能趋向于无穷大）。当 $r>d$ 时，有 $\phi(r)=-\epsilon_0(d/r)^6$，这样经过简单的积分可以证明

\begin{equation} a=4V_0\epsilon_0 N_A^2~. \end{equation}

　　

未完成：用集团展开推导范式方程的文章

2. 范德瓦尔斯等温线与相变

预备知识 2　相变平衡条件

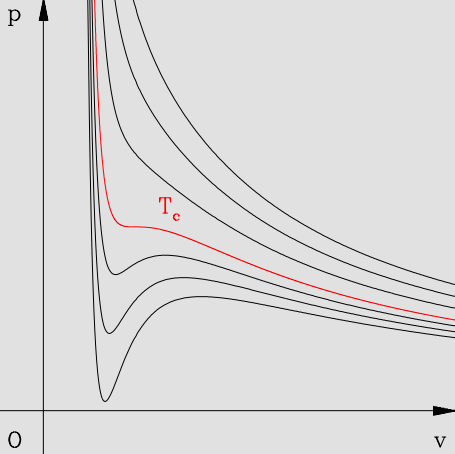
　　 范德瓦尔斯方程描述的系统的等温线如下图：

图
图 1：范德瓦尔斯气体等温线

　　 范德瓦尔斯方程的等价形式是

\begin{equation} V_m^3-V_m^2(b+\frac{RT}{p})+V_m\frac{a}{p}-\frac{ab}{p}=0~. \end{equation}

图
图 2：范德瓦尔斯的等温过程 MADBK

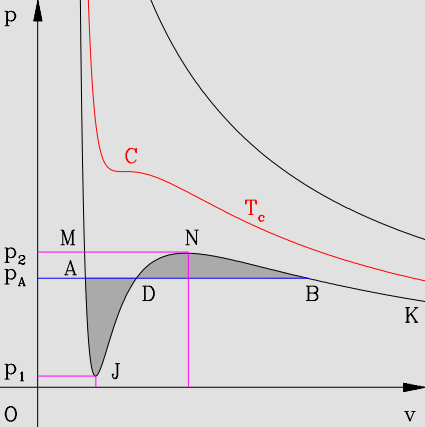
　　 这意味着在 $p-V$ 图上，一个压强 $p$ 可以对应 $3$ 个 $V$。以图 2 中的黑色等温曲线为例，当系统等温压缩从 $K$ 向 $B$ 过渡时，水蒸气的压强逐渐增大，但仍是气体。曲线 $B$ 到 $N$ 上的系统实际上是过冷气体，是亚稳态，稍加扰动后就会有液态水出现，形成水蒸气与液态水的共存态。同样地，$A$ 到 $J$ 是过热液体，稍加扰动将会产生水蒸气。因此等压水平线 $ADB$ 代表的是气液共存态，在从 $B$ 到 $D$ 到 $A$ 的等温压缩过程中，压强保持不变，水蒸气逐渐转化为液态水。到了 $A$ 点以后，水蒸气全部变为液态水，继续等温压缩，系统将沿着 $AM$ 曲线迅速 “爬升”。注意虽然 $AJDNB$ 也是范德瓦尔斯方程的解，但其中只有 $AJ$ 和 $NB$ 是亚稳态，它们分别代表过热液体和过冷气体，而 $JDN$ 曲线是不稳定地，不存在这样的系统。$ADB$ 虽然不是范德瓦尔斯方程的解，但是当前温度下稳定的气液共存态，

　　 对于给定的温度 $T$，气液相变时的压强对应图中水平线 $ADB$ 的高度，而 $T$ 与 $P$ 之间的关系满足克拉伯龙方程。事实上，压强 $P$ 还可以由麦克斯韦等面积法则来确定，即可以证明，图中的两个阴影部分面积是相等的。那么我们就可以由范德瓦尔斯方程先得出等温线，然后根据等面积法则画出水平线 $ADB$，即可得到当前温度下发生气液相变的压强。

　　 此外，范德瓦尔斯气体存在临界点。图中的红色曲线正是临界温度 $T_c$ 下的等温线，$C$ 点就是临界点。所谓临界温度，指的是在这一温度以上时，不再存在 $ADB$ 的气液共存态，事实上在临界温度以上，气相和液相的区别消失。这也意味着在 $C$ 处

\begin{equation} \left(\frac{\partial P}{\partial V}\right)_T=0~, \left(\frac{\partial^2 P}{\partial V^2}\right)_T=0~. \end{equation}
从范德瓦尔斯方程出发解上面两个方程可以得到临界点的压强和体积，式中包含常量 $a,b$，而通过临界点的测量得到 $a,b$。

习题 1　计算范德瓦尔斯气体的临界点

　　 利用式 4 和 式 5 计算临界点的压强和温度，用 $a,b,T$ 及相关常量来表示。

3. 范德瓦尔斯气体的稳定性，临界点的计算

预备知识 3　热动平衡判据，亥姆霍兹自由能，吉布斯自由能

　　 热力学系统的熵判据告诉我们，单元单相孤立系统的平衡稳定条件是

\begin{equation} c_v>0~,\ \left(\frac{\partial P}{\partial V} \right) _T<0~. \end{equation}
这样，我们就知道 $P$-$V$ 图中的等温线上只有斜率 $<0$ 的部分是平衡稳定的单相状态。其中 $NBK$ 是气态，$MAJ$ 是液态；而 $JDK$ 上的态是不稳定的，因此不存在。

　　 让我们进一步分析过热液体 $AJ$ 和过冷气体 $NB$ 的性质。虽然它们处于平衡稳定条件，但如果加以扰动，它们将迅速演变为气液共存态，落到 $ADB$ 水平线上。这是为什么呢？让我们研究这两个系统的某个热力学势，以亥姆霍兹自由能为判据，对于恒温恒容系统，平衡稳定态的条件为

\begin{equation} \left(\frac{\partial^2 F}{\partial V^2} \right) _T>0~. \end{equation}
利用 $ \,\mathrm{d}{F} =-S \,\mathrm{d}{T} -P \,\mathrm{d}{V} $，可得平衡稳定条件同式 6 一样。当 $F$ 关于 $V$ 的二阶导小于 $0$ 时，体系不稳定，如图 3 所示的 $SS'$ 的上凸部分，系统状态将自发地发生两相分离，使得自由能向更小的方向演化。也就是说，任意小的密度涨落都将导致自由能下降，最后到达两相分离的稳定态。这种由单相分解为两相的过程称为“失稳分解”。

图
图 3：失稳分解和成核长大示意图

　　 而对于范德瓦尔斯气体的过热液体 $AJ$ 段和过冷气体 $NB$ 段，虽然满足式 7 ，但经过扰动之后越过亚稳态的势垒，可以形成另一相的核，然后将逐渐扩大范围形成两相。如图 3 所示的 $P_LS$ 段，正代表过热液体，如果发生一定的扰动使得液体中产生气相的核，位于 $S'$ 右侧。那么原先的过热液体状态也就可以逐渐向 $P_L$ 演化，从而在保证恒容的同时使自由能更小。此过程中气相核将逐渐长大，两相最终分离。这个过程被称为“成核长大”。

　　 最后我们考察两相的化学势，即吉布斯自由能。利用 $ \,\mathrm{d}{\mu} =-S \,\mathrm{d}{T} +V \,\mathrm{d}{P} =V \,\mathrm{d}{P} $ 得到等温线上对应的化学势变化曲线。如图

图
图 4：化学势

　　 $A,B$ 对应温度 $T$ 下相变曲线两侧的液相和气相，相变发生的压强为 $P_A=P_B$。根据相变平衡条件，两点化学势应当相等，这也要求从 $A$ 沿着 $JDN$ 到 $B$ 过程中 $V \,\mathrm{d}{P} $ 的积分为 $0$，这就意味着图 2 中两个阴影部分的面积相同。这就是麦克斯韦等面积法则。

                     

© 小时科技 保留一切权利