Y-Δ 变换、星角变换
贡献者: coppersoulfate; addis
- 本文处于草稿阶段。
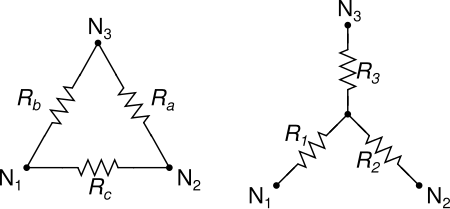
1三角形转星型电阻网络。可以简化一些复杂的电阻网络。
图 1:Δ 型(左)和 Y 型(右)电阻网络
Δ 转 Y
\begin{equation}
R_1 = \frac{R_b R_c}{R_s} ~,\qquad
R_2 = \frac{R_a R_c}{R_s} ~,\qquad
R_3 = \frac{R_a R_b}{R_s}~,
\end{equation}
Y 转 Δ
\begin{equation}
R_a = \frac{R_0}{R_1}~, \qquad
R_b = \frac{R_0}{R_2} ~,\qquad
R_c = \frac{R_0}{R_3}~,
\end{equation}
1. 证明
未完成。
简单的推导
在三端网络中有一端不接入电路时,应满足两端之间电阻相等。即:
\begin{equation}
\left\{\begin{matrix}R_1+R_2=\frac{1}{\frac{1}{R_c}+\frac{1}{R_a+R_b}}\\R_2+R_3=\frac{1}{\frac{1}{R_a}+\frac{1}{R_b+R_c}}\\R_3+R_1=\frac{1}{\frac{1}{R_b}+\frac{1}{R_c+R_a}}\end{matrix}\right.~,
\end{equation}
解以上方程即可得到 Y-Δ 变换。
比较严谨的证明
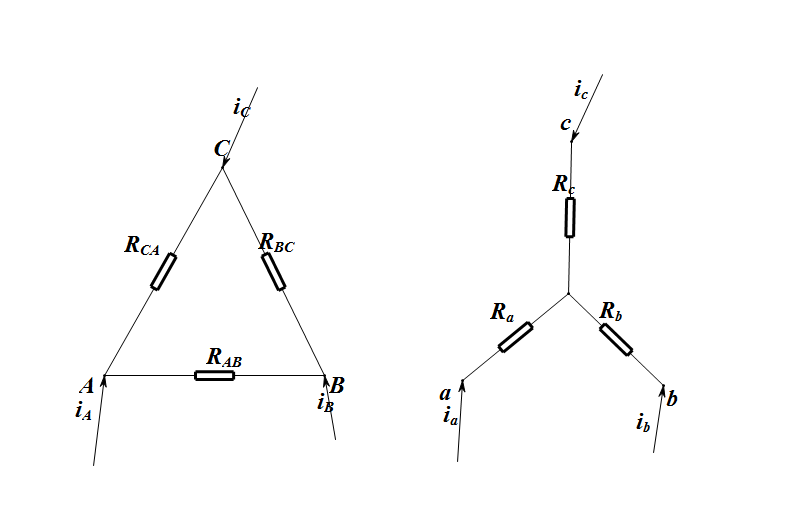
要使得 Y-Δ网络之间等价,应使得在三端接入任意电压时有对应一致的电流。
图 2:等效图
电流的正方向按图 2 定义。则应有:
\begin{equation}
\sum{i}=0~.
\end{equation}
\begin{equation}
i_{AB}=\frac{U_{AB}}{R_{AB}},i_{CA}=\frac{U_{CA}}{R_{CA}},i_A=i_{AB}-i_{CA}~,
\end{equation}
\begin{equation}
i_A=\frac{U_{AB}}{R_{AB}}-\frac{U_{CA}}{R_{CA}}~.
\end{equation}
\begin{equation}
i_a R_a-i_b R_b=U_{ab},i_c R_c-i_a R_a=U_{ca}~,
\end{equation}
\begin{equation}
i_a=\frac{R_c}{R_0}U_{ab}-\frac{R_b}{R_0}U_{ca}~.
\end{equation}
\begin{equation}
\frac{R_c}{R_0}U_{ab}-\frac{R_b}{R_0}U_{ca}=\frac{U_{AB}}{R_{AB}}-\frac{U_{CA}}{R_{CA}}~.
\end{equation}
\begin{equation}
R_{AB}=\frac{R_0}{R_c}~,
\end{equation}
\begin{equation}
R_{CA}=\frac{R_0}{R_b}~,
\end{equation}
\begin{equation}
R_{BC}=\frac{R_0}{R_a}~.
\end{equation}
\begin{equation}
R_c=\frac{R_{BC}}{R_{AB}}R_a~.
\end{equation}
\begin{equation}
R_b=\frac{R_{BC}}{R_{CA}}R_a~.
\end{equation}
\begin{equation}
R_a=\frac{R_{AB} R_{CA}}{R_{AB}+R_{BC}+R_{CA}}~,
\end{equation}