量子力学中的变分法、Rayleigh-Ritz 变分法

贡献者： addis

预备知识　定态薛定谔方程，拉格朗日乘数法

　　¹当平均能量是波函数的鞍点时，波函数就是能量的本征态。对一维单粒子

\begin{equation} E = \left\langle \psi \middle| H \middle| \psi \right\rangle ~, \end{equation}

但注意这里的波函数必须已经归一化。由于变分法需要假设任意的增量函数 $\delta \psi $，我们只好用一个不要求归一化的能量平均值公式

\begin{equation} E = \frac{ \left\langle \psi \middle| H \middle| \psi \right\rangle }{ \left\langle{\psi}\middle| \psi \right\rangle }~, \end{equation}

该式可以给出基态波函数的能量上限。

　　现在假设波函数增加 $\delta \psi$

\begin{equation} E \left\langle \delta\psi \middle| \psi \right\rangle + E \left\langle \psi \middle| \delta\psi \right\rangle = \left\langle \delta \psi \middle| H \middle| \psi \right\rangle + \left\langle \psi \middle| H \middle| \delta\psi \right\rangle ~. \end{equation}

由于 $\delta\psi$ 是任意的，我们也可以使用 $ \mathrm{i} \delta\psi$

\begin{equation} -E \left\langle \delta\psi \middle| \psi \right\rangle + E \left\langle \psi \middle| \delta\psi \right\rangle = - \left\langle \delta\psi \middle| H \middle| \psi \right\rangle + \left\langle \psi \middle| H \middle| \delta\psi \right\rangle ~. \end{equation}

以上两式等效，两式相减，得（相当于 $\psi^*$ 与 $\psi$ 是两个独立的变量函数）

\begin{equation} E \left\langle \delta\psi \middle| \psi \right\rangle = \left\langle \delta\psi \middle| H \middle| \psi \right\rangle ~, \end{equation}

该式对任意微小函数增量 $\delta\psi $ 都要求成立。现在如果令 $\delta \psi = \delta (x)$，我们得到薛定谔方程

\begin{equation} H \left\lvert \psi \right\rangle = E \left\lvert \psi \right\rangle ~, \end{equation}

归一化条件下的变分法也可以由拉格朗日乘数法完成，令

\begin{equation} L = \left\langle \psi \middle| H \middle| \psi \right\rangle - \lambda [ \left\langle{\psi}\middle| \psi \right\rangle - 1]~. \end{equation}

类似以上过程，同样有

\begin{equation} \left\langle \delta\psi \middle| H \middle| \psi \right\rangle - \lambda \left\langle \delta\psi \middle| \psi \right\rangle = 0~. \end{equation}

即

\begin{equation} H \left\lvert \psi \right\rangle = \lambda \left\lvert \psi \right\rangle ~. \end{equation}

显然，乘数 $\lambda $ 就是本征态能量。

1. Rayleigh-Ritz 变分法

　　用一些变分参数拟合波函数 $ \left\lvert \psi \right\rangle $，然后找到这些参数使式 2 最小化的值。

　　特殊地，令

\begin{equation} \psi = \sum_n c_n \chi_n~. \end{equation}

代入式 2 ，令对每个 $c_n$ 求导为零，得

\begin{equation} \sum_n ( \left\langle \chi_n' \middle| H \middle| \chi_n \right\rangle - \left\langle \chi_n' \middle| \chi_n \right\rangle E)c_n = 0 \qquad (n' = 1,2,\dots,N)~. \end{equation}

为了让该方程有解，

\begin{equation} \det[ \left\langle \chi_n' \middle| H \middle| \chi_n \right\rangle - \left\langle \chi_n' \middle| \chi_n \right\rangle E] = 0~, \end{equation}

解得能量 $E_0^{(N)}, E_1^{(N)},\dots,E_{n-1}^{(N)}$。

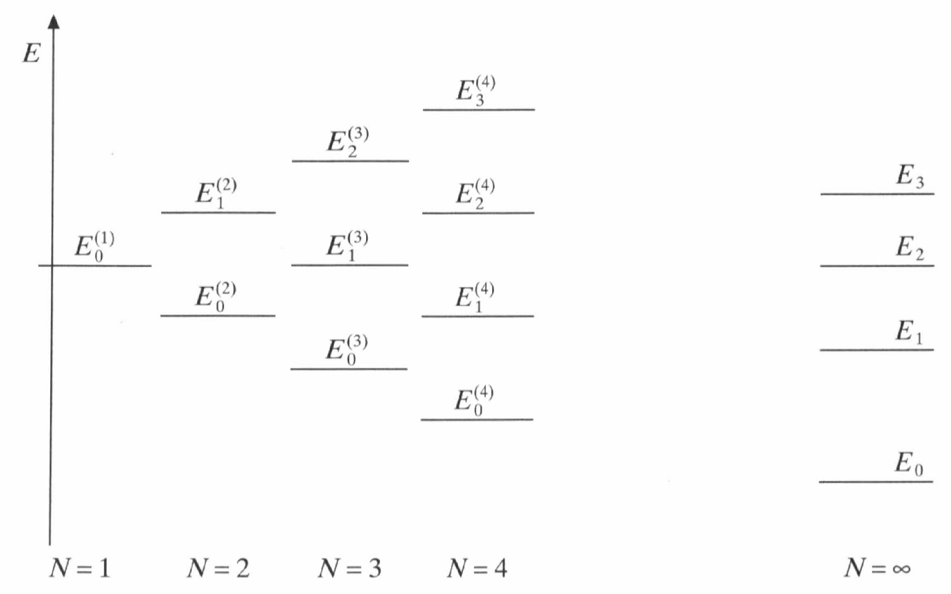
　　根据 Hylleraas-Undheim 理论，相邻两个 $N$ 的两组能级一定是交错的（图 1 ），所以每个 $E_0^{(N)}$ 都大于对应本征值 $E_0^{(\infty)}$。

图 1：Hylleraas-Undheim 理论

1. ^ 参考 [1]。

[1] ^ Bransden, Physics of Atoms and Molecules, 2ed