2015 年考研数学试题（数学一）

贡献者：待更新

1. 选择题

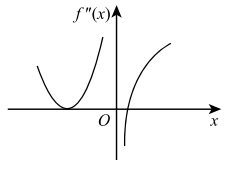
设函数 $f(x)$ 在 $(-\infty,+\infty)$ 上连续，其 2 阶导函数 $f''(x)$ 的图形如图 1 所示，则曲线 $y=f(x)$ 的拐点个数为 ($\quad$)
(A)$\quad$0 $\quad$ (B)$\quad$1 $\quad$ (C)$\quad$2 $\quad$(D)$\quad$3

图 1
设 $y=\frac{1}{2}e^{2x}+(x-\frac{1}{3})e^x$ 是二阶常系数非齐次线性微分方程 $y''+ay'+by=ce^x$ 的一个特解,则($\quad$)
(A) $a=-3,b=2,c=-1$
(B) $a=3,b=2,c=-1$
(C) $a=-3,b=2,c=1$
(D) $a=3,b=2,c=1$
若级数 $\displaystyle \sum_{n=1}^\infty a_n $ 条件收敛，则 $x=\sqrt{3}$ 与 $x=3$ 依次为幂级数 $\displaystyle \sum_{n=1}^\infty na_n(x-1)^n$ 的($\quad$)
(A) 收敛点，收敛点
(B) 收敛点，发散点
(C) 发散点，收敛点
(D) 发散点，发散点
设 $D$ 是第一象限中的曲线 $2xy=1,4xy=1$ 与直线 $y=x,y=\sqrt{3}x$ 围成的平面区域，函数 $f(x,y)$ 在 $D$ 上连续，则 $\displaystyle {\iint}_D f(x,y) \,\mathrm{d}{x} \,\mathrm{d}{y} $=($\quad$)
(A)$\displaystyle \int_\frac{\pi}{4}^\frac{\pi}{3} \,\mathrm{d}{\theta} \int_\frac{1}{2\sin 2\theta}^\frac{1}{\sin 2\theta}f(r\cos \theta,r\sin \theta)r \,\mathrm{d}{r} $
(B)$\displaystyle \int_\frac{\pi}{4}^\frac{\pi}{3} \,\mathrm{d}{\theta} \int_\frac{1}{\sqrt{2\sin 2\theta}}^\frac{1}{\sqrt{\sin 2\theta}}f(r\cos \theta,r\sin \theta)r \,\mathrm{d}{r} $
(C) $\displaystyle \int_\frac{\pi}{4}^\frac{\pi}{3} \,\mathrm{d}{\theta} \int_\frac{1}{2\sin 2\theta}^\frac{1}{\sin 2\theta}f(r\cos \theta,r\sin \theta) \,\mathrm{d}{r} $
(D)$\displaystyle \int_\frac{\pi}{4}^\frac{\pi}{3} \,\mathrm{d}{\theta} \int_\frac{1}{\sqrt{2\sin 2\theta}}^\frac{1}{\sqrt{\sin 2\theta}}f(r\cos \theta,r\sin \theta) \,\mathrm{d}{r} $
设矩阵 $ \boldsymbol{\mathbf{A}} = \begin{pmatrix}1&1&1\\1&2&a\\1&4&a^2\end{pmatrix} , \boldsymbol{\mathbf{b}} = \begin{pmatrix}1\\d\\d^2\end{pmatrix} $ 若集合 $\Omega=\{1,2\}$ 则线性方程组 $ \boldsymbol{\mathbf{Ax=b}} $ 有无穷多解的充分必要条件为($\quad$)
(A) $a\notin \Omega,d\notin \Omega$
(B) $a\notin \Omega,d\in \Omega$
(C) $a\in \Omega,d\notin \Omega$
(D) $a\in \Omega,d\in \Omega$
设二次型 $f(x_1,x_2,x_3)$ 在正交变换 $x=Py$ 下的标准型为 $2y_1^2+y_2^2-y_3^2$，其中 $P=(e_1,e_2,e_3)$。若 $Q=(e_1,-e_3,e_2)$，则 $f(x_1,x_2,x_3)$ 在正交变换 $x=Qy$ 下的标准形为($\quad$)
(A) $2y_1^2-y_2^2+y_3^2$
(B) $2y_1^2+y_2^2-y_3^2$
(C) $2y_1^2-y_2^2-y_3^2$
(D) $2y_1^2+y_2^2+y_3^2$
若 $A,B$ 为任意两个随机事件，则($\quad$)
(A) $P(AB)\le P(A)P(B)$
(B) $P(AB) \ge P(A)P(B)$
(C) $\displaystyle P(AB)\le \frac{P(A)+P(B)}{2}$
(D) $\displaystyle P(AB)\ge \frac{P(A)+P(B)}{2}$
设随机变量 $X,Y$ 不相关，且 $E(X)=2,E(Y)=1,D(X)=3$ ，则 $E[X(X+Y-2)]$=($\quad$)
(A) -3
(B) 3
(C) -5
(D) 5

2. 填空题

$\displaystyle \lim_{x \to 0} \frac{ \ln\left(\cos x\right) }{x^2}$=($\quad$)
$\displaystyle \int_\frac{-\pi}{2}^\frac{\pi}{2}(\frac{\sin x}{1+\cos x}+ \left\lvert x \right\rvert ) \,\mathrm{d}{x} $=($\quad$)
若函数 $z=z(x,y)$ 由方程 $e^z+xyz+x+\cos x=2$ 确定，则 $ \,\mathrm{d}{z} |_{(0,1)}$=($\quad$)
设 $\Omega$ 是由平面 $x+y+z=1$ 与三个坐标平面所围成的空间领域，则 $\displaystyle {\iiint}_{\Omega}(x+2y+3z) \,\mathrm{d}{x} \,\mathrm{d}{y} \,\mathrm{d}{z} $=($\quad$)
$n$ 阶行列式 $\left|\begin{array}{ccccc}2 & 0 & \cdots & 0 & 2 \\ -1 & 2 & \cdots & 0 & 2 \\ \vdots & \vdots & & \vdots & \vdots \\ 0 & 0 & \cdots & 2 & 2 \\ 0 & 0 & \cdots & -1 & 2\end{array}\right|$=($\quad$)
设二维随机变量 $(X,Y)$ 服从正态分布 $N(1,0;1,1;0)$ ，则 $P\{XY-Y<0\}$=($\quad$)

3. 简答题

设函数 $f(x)=x+a \ln\left(1+x\right) +bx\sin x$，若 $f(x)$ 与 $g(x) $ 在 $x \to 0$ 时是等价无穷小，求 $a,b,k$ 值。
设函数 $f(x)$ 在定义域 $I$ 上的导数大于零，若对于任意的 $x_0 \in I$，曲线 $y=f(x)$ 在点 $(x_0,f(x_0))$ 处的切线与直线 $x=x_0$ 及 $x$ 轴所围成区域的面积恒为 4，且 $f(0)=2$，求 $f(x)$ 的表达式。
已知函数 $f(x, y)=x+y+x y$, 曲线 $C: x^2+y^2+x y=3$, 求 $f(x, y)$ 在曲线 $C$ 上的最大方向导数。
(1)设函数 $u(x), v(x)$ 可导, 利用导数定义证明 $[u(x) v(x)]^{\prime}=u^{\prime}(x) v(x)+u(x) v^{\prime}(x)$;
(2)设函数 $u_1(x), u_2(x), \cdots, u_n(x)$ 可导, $f(x)=u_1(x) u_2(x) \cdots u_n(x)$, 写出 $f(x)$ 的求导公式。
已知曲线 $L$ 的方程为 $\left\{\begin{array}{l}z=\sqrt{2-x^2-y^2}, \\ z=x,\end{array}\right.$ 起点为 $A(0, \sqrt{2}, 0)$, 终点为 $B(0,-\sqrt{2}, 0)$, 计算曲线积分 $I=\int_L(y+z) \mathrm{d} x+\left(z^2-x^2+y\right) \mathrm{d} y+x^2 y^2 \mathrm{~d} z$。
设向量组 $\alpha_1,\alpha_2,\alpha_3$ 为 $R^3$ 的一个基,$\beta_1=2\alpha_1+2k\alpha_3,\beta_3=\alpha_1+(k+1)\alpha_3$.
(1)证明向量组 $\beta_1,\beta_2,\beta_3$ 为 $R^2$ 的一个基。
(2)当 $k$ 为何值时，存在非零向量 $\xi$ 在基 $\alpha_1,\alpha_2,\alpha_3$ 与基 $\beta_1,\beta_2,\beta_3$ 下的坐标相同，并求所有的 $\xi$。
设矩阵 $ \boldsymbol{\mathbf{A}} = \begin{pmatrix}0&2&-3\\-1&3&-3\\1&-1&a\end{pmatrix} $ 相似于矩阵 $ \boldsymbol{\mathbf{B}} = \begin{pmatrix}1&-2&0\\0&b&0\\0&3&1\end{pmatrix} $。
(1)求 $a,b$ 的值；
(2)求可逆矩阵 $ \boldsymbol{\mathbf{P}} $，使 $ \boldsymbol{\mathbf{P^{-1}AP}} $ 为对角矩阵。
设随机变量 $X$ 的概率密度为 $f(x)= \left\{\begin{aligned} 2^{-x}\ln 2,\quad x>0\\0, \quad x\le 0 \end{aligned}\right. $ 对 $X$ 进行独立重复的观测，直到第 2 个大于 3 的观测值出现时停止，记 $Y$ 为观测次数。
(1)求 $Y$ 的概率分布；
(2)求 $E(Y)$。
设总体 $X$ 的概率密度为 $f(x;\theta)= \left\{\begin{aligned} \frac{1}{1-\theta}, && \theta \le x\le 1\\ 0,&& \text{其他} \end{aligned}\right. $ 其中 $\theta$ 为未知参数，$X_1,X_2,\dots ,X_n$ 为来自该总体的简单随机样本。
(1)求 $ \theta $ 的矩估计量；
(2)求 $ \theta$ 的最大似然估计量。