天体物理中 N 体问题的数值计算（Matlab）

贡献者： addis

本文处于草稿阶段。

预备知识　四阶龙格库塔法，用 Matlab 生成 mp4 视频

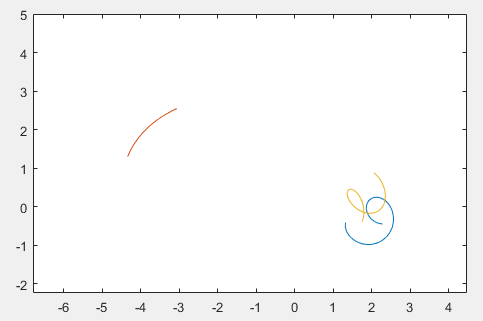
图 1：平面三体运动的模拟，动画见这里。

　　这里给出一个简单的程序，在实际科研中，往往需要大量并行计算，且考虑许多其他因素，详见 “N 体问题（天体物理）”。

　　数值解常微分方程组

\begin{equation} \boldsymbol{\mathbf{a}} _i = \ddot{ \boldsymbol{\mathbf{r}} _i} = \frac{ \boldsymbol{\mathbf{F}} _i}{m_i}~. \end{equation}

\begin{equation} \boldsymbol{\mathbf{F}} _i = G\sum_{j\ne i} \frac{m_i m_j( \boldsymbol{\mathbf{r}} _j - \boldsymbol{\mathbf{r}} _i)}{ \left\lvert \boldsymbol{\mathbf{r}} _j - \boldsymbol{\mathbf{r}} _i \right\rvert ^3}~. \end{equation}

　　算法 “四阶龙格库塔法” 中的 keplerRK4.m 相似，只是使用了 Matlab 自带的变步长龙格库塔解算器 ode45，效率更高。另外当两个天体距离太近，使得 $ \boldsymbol{\mathbf{F}} _i$ 超过了双精度的最大值时，程序将报错终止。

　　当设置 Ndim = 2，程序中所有的位置、速度、力都是二维矢量，当 Ndim = 3 时都是三维矢量。

代码 1：n_body.m

% N 体问题（支持二维或三维）
% Ndim: 2 维或 3 维运动
% r0: 初始位置矢量， Ndim*N 矩阵（N 是质点数）
% v0: 初始速度矢量， Ndim*N 矩阵
% m: 质量， 1*N 矩阵
% t: 时间网格
% RelTol: 微分方程解算器的精度
function [r, v] = n_body(r0, v0, m, Ndim, t, G, RelTol)
N = numel(m);
Y0 = [r0(:), v0(:)];
options = odeset('RelTol', RelTol);
[T, Y] = ode45(@(t,Y)ode_fun(t, Y, m, G, Ndim), ...
        [min(t),max(t)], Y0, options);
r = zeros(numel(t),Ndim,N); v = r;
k1 = 0; k2 = N*Ndim;
for i = 1:N
    for j = 1:Ndim
        k1 = k1 + 1; k2 = k2 + 1;
        r(:,j,i) = interp1(T, Y(:, k1), t);
        v(:,j,i) = interp1(T, Y(:, k2), t);
    end
end
end

% 已知天体位置和速度， 计算加速度
function dY = ode_fun(~, Y, m, G, Ndim)
N = numel(Y)/(2*Ndim);
r = reshape(Y(1:Ndim*N), Ndim, N);
v = reshape(Y(Ndim*N+1:end), Ndim, N);
a = zeros(Ndim, N);
for i = 1:N
    F = 0;
    for j = 1:N
        if j == i, continue; end
        r_ij = r(:,j) - r(:,i);
        d_ij = sqrt(sum(r_ij.^2));
        F = F + G*m(i)*m(j)*r_ij/d_ij^3;
        if isinf(F)
            error('发生碰撞!');
        end
    end
    a(:, i) = F/m(i);
end
dY = [v(:); a(:)];
end

　　下面演示平面三体运动，并制作 MP4 动画。

代码 2：three_body.m

% 平面三体运动演示
% === 参数设置 ===
r0 = [-1,0; 1,0; 0,sqrt(3)+0.01]';
v0 = [r0(:,3)-r0(:,2); r0(:,1)-r0(:,3); r0(:,2)-r0(:,1)]'*0.35;
m = [1,1,1];
RelTol = 1e-6;
G = 1;
tmin = 0; tmax = 160; Nt = 3000;
plot_step = 10;
Ntail = 100; % 尾巴长度

% 写 mp4 视频
v = VideoWriter('3body', 'MPEG-4');
v.FrameRate = 10; % 默认 30
v.Quality = 25; % 默认 75
% ===============
close all;
open(v);

t = linspace(tmin, tmax, Nt);
[r, ~] = n_body(r0, v0, m, 2, t, G, RelTol);
figure;
ax = [min(min(r(:,1,:))), max(max(r(:,1,:))), ...
    min(min(r(:,2,:))), max(max(r(:,2,:)))]*1.1;
for it = 1:plot_step:Nt
clf;
for i = 1:3
    it0 = max(1,it-Ntail);
    plot(r(it0:it,1,i), r(it0:it,2,i)); hold on;
    axis equal;
end
axis(ax);
frame = getframe(gcf);
writeVideo(v, frame);
end
close(v);