神经网络

贡献者： xzllxls

　　 神经网络（Neural network, NN），准确地说，是人工神经网络（Artificial neural network, ANN），在机器学习领域中是指 “由具有适应性的简单单元组成的广泛并行互联的网络，其组织能够模拟生物神经系统对真实世界物体所做出的交互反应”[1]。

　　神经网络是机器学习中广泛使用的一种基本方法。该方法具有较好的曲线拟合能力，能够从数据中学习离散型、连续型或者向量型函数。

1. 动机

　　神经网络最初是受到生物神经系统结构的启发，而提出的机器学习模型。生物的神经系统，比如人脑，从结构上讲，是由大量的基本单位——神经元通过各种复杂的互相连接而构成。从功能的角度，神经系统中的每个神经元都可以接收别的神经元传来的信号，然后做出处理，将处理后的结果，通过信号发送给其它与之连接的神经元。大量神经元能够同时协调工作，从而使得整个神经系统具有对各种环境刺激做出反应的能力，即智能（Intelligence）。

　　由此，人们受到启发，如果能够模拟生物神经系统的结构，并赋予其类似的信息传送和处理机制，则可以定义一个能够具有一定智能的数学模型。值得注意的是，虽然人工神经网络最初的想法是受到生物学的启发，但是在其后续实际研究过程中，站在计算机科学家的角度上来说，并不追求在每一个细节上都模拟生物神经系统。例如，人工神经元输出单一不变的值，然而生物神经元输出的是复杂的时序脉冲[2]。

2. 基本结构

1.神经元

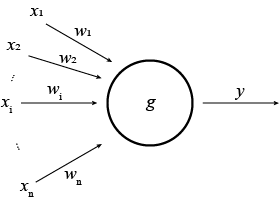
　　生物神经系统的基本单位是神经元，能够接收、处理和发送信号。人们将生物神经元抽象出一个简单模型，即人工神经元（Artificial neuraon），在机器学习领域内，通常就称神经元（Neuron）。在该模型中，神经元接收到其它多个神经元传来的输入信号，这些输入信号通过带有权重的连接进行传递，神经元接收到的总输入值将与神经元的阈值进行比较，然后通过激活函数处理以产生神经元的输出[3]。

图 1：神经元示意图

　　神经元的基本结构如图 1 所示。其中，$x_1, x_2, ..., x_i, ..., x_n$ 表示神经元的输入，$w_1, w_2, ..., w_i, ..., w_n$ 表示每个输入所对应的权重，$g$ 为激活函数，$w_0$ 为偏移量，$y$ 为神经元的输出值。输出和输入的关系是

\begin{equation} y=g(w_1x_1+w_2x_2+...+w_ix_i+...+w_nx_n+w_0).~ \end{equation}

也可以写成向量形式：

\begin{equation} y=g( \boldsymbol{\mathbf{w}} \boldsymbol{\mathbf{x}} ).~ \end{equation}

其中，$ \boldsymbol{\mathbf{w}} =(w_0, w_1, w_2, ..., w_i, ..., w_n)$，$ \boldsymbol{\mathbf{x}} =(x_0, x_1, x_2, ..., x_i, ..., x_n)$，$x_0=1$.

2.感知机与前馈神经网络

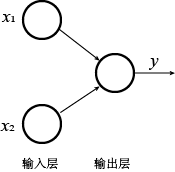
　　 感知机（Perceptron）是有两层神经元构成的最简单的神经网络。其结构中主要包含输入层和输出层。输入层能够接收外界传送来的输入信号，并传递给输出层。输出层就是一个神经元，功能是接收来自输入层传递来的信号，然后做出处理，并输出结果。

图 2：简单的感知机示意图

　　图 2 表示的是一个简单的感知机。其中有两层，分别为输入层和输出层。输入层有两个输入神经元，分别接收输入信号 $x_1$ 和 $x_2$。输出层有一个输出神经元，产生输出结果 $y$。此感知机的输入层只是接收输入数据而不做处理，只有输出层的那个神经元有计算功能，因此，该感知机只有一层功能神经元（Functional neuron）。

　　感知机能够表示所有的原子逻辑函数：与（AND）、或（OR）、与非（NAND）、或非（NOR）[2]。然而，对于某些逻辑函数，单一的感知器无法表示。比如，异或运算。

图 3：逻辑与问题 $x_1x_2$

图 4：逻辑或问题

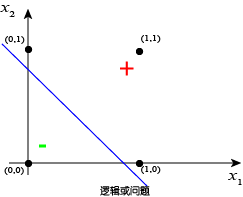
　　图 3 和图 4 分别表示的是两个输入变量 $x_1$,$x_2$ 之间的逻辑与问题（$x_1 \wedge x_2$）和逻辑或问题（$x_1 \vee x_2$）。这两个基本的布尔运算很容易由感知机解决。

图 5：异或问题

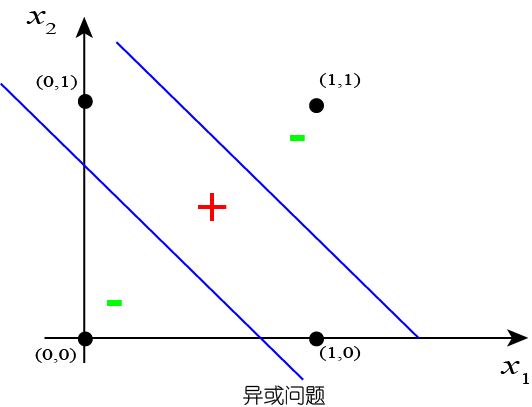
　　图 5 表示的是异或问题（$x_1 \oplus x_2$）。这是一个非线性可分问题，靠单一的感知器无法解决。

　　感知机可以堆叠，层数也能加深，每层也可以有多个神经元。由多层神经元堆叠而成的具有层级结构的神经网络，称为多层感知机（Multi-layer perceptron, MLP），或者前馈神经网络（Feedforward neural network）。之所以称之为 “前馈” 神经网络，是因为数据在网络中的流动方向始终是单向的，数据从浅层网络向深层网络传播，而不会返回。在多层网络结构中，只有相邻层的神经元之间才有连接，同一层的神经元之间是没有连接的，跨层的神经元也不会互相连接。

图 6：两层感知机

　　图 6 表示的是一个简单的多层网络。其中，中间一层为隐含层（Hidden layer）。原始的输入信号，经过隐含层的处理，送到输出层，再由输出层做处理，最终产生结果作为整个网络的输出值。网络的输入层不对数据做处理，只有中间的隐含层和最后的输出层对数据做加工处理。因此，该网络拥有两层功能神经元。通常将具有两层功能神经元的感知机，称为 “两层感知机”，或者 “两层网络”，也有文献称其为 “单隐层网络”。

　　隐含层的存在使得神经网络具有非线性可分的能力。事实上，两层感知机就能表示所有的逻辑函数[2]。隐含层的神经元的激活函数具有非线性性。将激活函数作用于线性变换的输出能够产生非线性变换[4]。

3. 感知机训练算法

　　有了基本的感知机结构，如何利用其来学习拟合实际数据呢？这就须要一套感知机训练算法。训练算法能够根据感知机输出的值与真实值之间的差异来调节感知机的权值参数，从而实现学习。

　　权值调整规则为：

\begin{equation} w_i \leftarrow w_i + \Delta w_i~ \end{equation}

\begin{equation} \Delta w_i = \eta(y-y_o)x_i~ \end{equation}

其中：$x_i$ 表示第 $i$ 个输入神经元，$w_i$ 表示第 $i$ 个输入的权值，$y$ 表示训练数据，$y_o$ 表示感知机的输出值，$\eta$ 表示学习率，取值范围为 $(0,1)$。

　　式 3 和式 4 为权值参数一次更新过程。当感知机输出值与训练样本有误差时，训练算法会反复迭代上述过程，从而使得感知机输出值逐步逼近训练样本。感知机权值的初始值可以统一设定为一个常数，也可以随机设置。在训练过程中，学习率 $\eta$ 可能会随着迭代次数的增加而逐渐减少，从而避免模型越过极小值点。

　　感知机训练算法十分简单，可以解决线性可分问题的训练，但不适用于非线性可分问题。现代神经网络训练最常用的方法是梯度下降及其各种改进方法。

　　理论上说，神经网络模型中的权值，也就是模型参数的数量越多，模型越复杂，其学习能力就越强。现代深度学习技术采用深度神经网络，其结构中所包含的隐含层数量通常有八九层甚至更多[3]。

　　对于较为复杂的模型，如果训练样本数较少，则容易产生过度拟合。随着模型层数的增加，模型复杂度显著提高，模型训练所须要的计算成本也大大增加。然而，当今时代是互联网、大数据时代，数据无处不在，海量数据能够避免模型训练的过度拟合。近些年来，随着芯片技术的飞速发展，基于图形处理器的并行计算技术在深度学习模型训练方面获得了广泛应用，从而使得复杂模型的实现与训练成为可能。由于，数据和算力的保证，深度学习技术获得了大规模的普及和应用。

参考文献

T. Kohonen, “An introduction to neural computing,” Neural Networks, vol. 1, no. 1, pp. 3–16, 1988.
T. M. Mitchell, Machine learning. 1997.
周志华. 机器学习[M]. 北京：清华大学出版社. 2016: 97
I. Goodfellow, Y. Bengio, and A. Courville, Deep learning. MIT press, 2016: 174.