激活函数
贡献者: xzllxls; addis
激活函数(Activation function)是人工神经元计算流程的最后一步,跟随在仿射变换之后的一个非线性变换。神经元中的仿射变换是带有参数的,参数的值是模型训练时学习而来的。而激活函数往往是一个无参数的固定的非线性变换,它决定着一个神经元输出的值的范围。
神经网络中能够采用的激活函数种类繁多,往往须要根据实际应用场景做选择。设激活函数为 $g$ 的输入为 $x$,输出为 $y$,有 $y=g(x)$。
1. 恒等函数
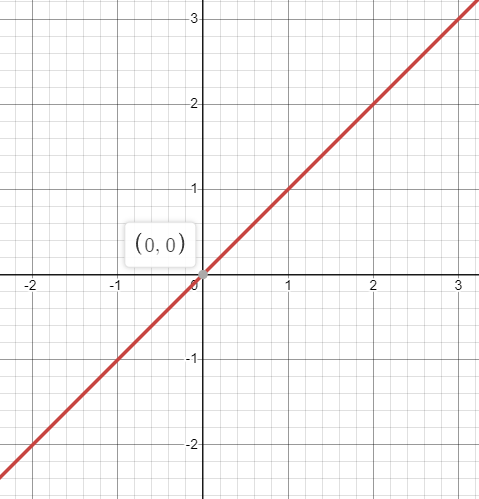
显然,恒等函数的表达式为:
\begin{equation}
y=g(x)=x~.
\end{equation}
图 1:恒等函数
导数为:
\begin{equation}
g'(x)=1~.
\end{equation}
2. 阶跃函数
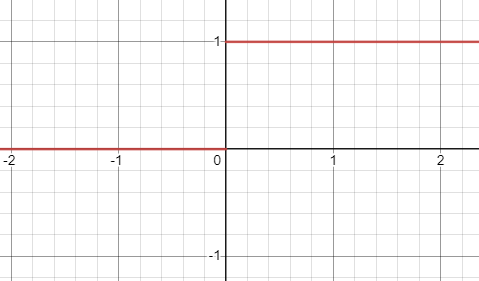
阶跃函数的表达式为:
\begin{equation}
g'(x)= \left\{\begin{aligned} 1, x \geqslant 0 \\ 0, x < 0 \end{aligned}\right. ~
\end{equation}
图 2:阶跃函数
导数为:
\begin{equation}
g'(x)= \left\{\begin{aligned} 0, x \neq 0 \\ \text{不存在}, x = 0 \end{aligned}\right. ~
\end{equation}
3. S 型函数
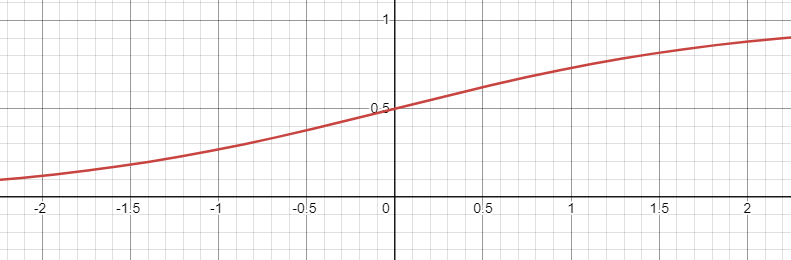
S 型函数又称为 Sigmoid 函数。表达式为:
\begin{equation}
y=g(x)=\frac{1}{1+e^{-x}}~.
\end{equation}
图 3:Sigmiod 函数图像
其导数为:
\begin{equation}
g'(x)=g(x)(1-g(x))~.
\end{equation}
4. 双曲正切函数
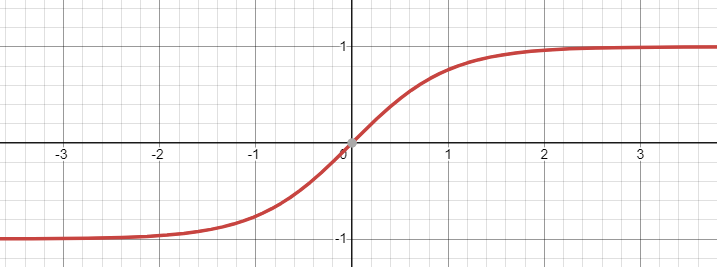
双曲正切函数表达式为:
\begin{equation}
y=g(x)= \tanh\left(x\right) =\frac{e^x-e^{-x}}{e^x+e^{-x}}~.
\end{equation}
图 4:双曲正切函数
导数为:
\begin{equation}
g'(x)=1-g^2(x)~.
\end{equation}
5. 线性整流单元
在现代深度神经网络的架构中,最常用的激活函数是线性整流单元(Rectified linear unit, ReLU)。其表达式为:
\begin{equation}
y=g(x)=\max\{0,x\}~.
\end{equation}
在 TensorFlow 中,可以用以下函数实现线性整流单元:
tf.nn.relu(Tensor, name)
参数含义:
- Tensor:输入张量
- name:该操作的名称(可选)
返回值的数据类型为 Tensor 张量。
例子:
import tensorflow as tf
result = tf.nn.relu([2., -1., 0.]).numpy()
print(result)
array([2., 0., 0.], dtype=float32)
从上述代码和执行结果可以看出,tf.nn.relu 函数对于输入张量的每个分量做线性整流处理。输入张量 $[2, -1, 0]$ 的三个分量中的 $2$ 是大于 $0$ 的,因此结果张量中的第 $1$ 个分量为 $2$;第 $2$ 分量为 $-1$,小于 $0$,因此计算后的结果为 $0$;第 $3$ 个分量为 $0$,计算结果显然为 $0$。