数值解线性方程组(入门)
贡献者: addis
1求解线性方程组是科学计算中最普遍也是最为常见的问题,几乎所有与科学计算有关的问题都直接或间接与它有关。不论是常微分方程,偏微分方程,非线性方程,最优化,甚至是图像和信号处理,机器学习等等问题,最终都会转化成求解线性方程组。因此,线性方程组的解法也是科学计算领域里研究最广泛的问题之一。
线性方程的数值解法按照求解过程可以分为:直接法(direct method)和迭代法(iterative method)。其中,直接法顾名思义就是直接求得方程组的解,这个解在很多情况下就是方程组的解析解。一般常用直接法为高斯消元法(Gauss elimination)或者是 LU 分解(LU decomposition)。
而相对应的,迭代法则是通过有限次的迭代,将数值解不断逼近解析解的过程。因此,迭代法通常都会引入一定的误差。这些误差可以通过增加迭代次数和改进方法逐渐逼近于机器精度。目前常见的迭代法包含了:雅可比法(Jacobi method),高斯-赛德尔迭代(Gauss-Seidel method),Krylov 子空间法(Krylov subspace methods)等。由于迭代法对于数值代数的要求较高,这里就不做过多展开了。有兴趣的同学可以在下面留言,我会单独开一个子专栏进行讨论。
1. 高斯消元法和 LU 分解
事实上,高斯消元法的过程就是构造 LU 分解的上下三角矩阵的过程。关于这个高斯消元法的基本算法见 “高斯消元法解线性方程组” 或参考 Wikipedia 相关页面。
这里我想从更宏观的角度来分析一下高斯消元法和 LU 分解。这个方法的主要思路包含三步,以求解 $Ax=b$ 为例,我们接下来逐一解释。注意,这里的 $A$ 是一个 $n\times n$ 的矩阵,$x$ 和 $b$ 都是 $n\times1$ 的向量。
基本的消元运算
通过高斯消元或者 LU 分解,得到 $A=LU$,其中 $L$ 和 $U $ 分别是 $n\times n$ 的上,下三角矩阵。我们将 $A$ 中第 $i$ 行,第 $j$ 列的元素记做 $a_{i,j}$,那么消元的算法(伪代码)如下
for k=1:n-1
if a(k,k) not 0
for i=k+1:n
L(i,k) = a(i,k)/a(k,k)
end
for j=k+1:n
for i=k+1:n
a(i,j) = a(i,j)-L(i,k)*a(k,j)
end
end
end
end
经过消元得到新的 $A$ 矩阵实际上就是 LU 分解中的上三角 $U$ 矩阵。而在消元过程中用于临时存储系数的 $L$ 矩阵,加上一个单位矩阵就可以得到 LU 分解的下三角矩阵。事实上,细心的同学可以发现,这样的 LU 分解可以直接在 $A$ 的存储空间上进行,无需额外的内存。
经过简单的计算,这样的消元过程总共需要进行 $\sum_{k=1}^{n-1}(k+2k^2)\approx \frac{2}{3}n^3$ 次浮点运算。
前向替换(forward substitution)
把 $Ux$ 看做一个整体 $y$,将求解 $Ax=b$ 转化为求解 $LUx=Ly=b$。由于 $L $ 是下三角矩阵,它的第一行只有一个非 0 的元素 $L_{1,1}$,因此这个求解过程可以简单的从第一行开始,逐行替换。
那么,整个的替换过程需要 $1+3+5+...+(2n-1)=n^2$ 次浮点运算。
后向替换(backward substitution)
最后,我们利用从2.中得出的 $y$ , 求解 $Ux=y$,从而得到原本的未知数 $x$。这个过程正好和求解下三角矩阵相反,需要从最后一行开始,依次向上。
同样的,它也需要 $n^2$ 次浮点运算。
2. 小结
这样看起来,我们把求解一个线性方程组的问题转化成了一个 LU 分解和求解两个线性方程组,但是由于 $L$ 和 $U$ 都是三角矩阵,它们的求解过程非常简单,因此整个过程的总体运算复杂度始终是由 LU 分解所主导,即为 $\mathcal{O}(n^3)$。
例子 1
让我们来用下面的代码直接测试一下高斯消元法的运算复杂度。
import numpy as np
import scipy
import scipy.linalg # SciPy Linear Algebra Library
import timeit
import matplotlib.pyplot as plt
NList = np.arange(1,17)*500
# Loop for all N
invTime = []
for i in NList:
A = scipy.random.rand(i,i)
b = scipy.random.rand(i,1)
invTimeTemp = %timeit -r 5 -n 1 -o x = scipy.linalg.solve(A, b)
invTime.append(invTimeTemp)
# Plot
fig, ax = plt.subplots(1)
xp = []
yp = []
for (i, t) in zip(NList,invTime):
xp.append(i)
yp.append(t.average)
p3 = np.poly1d(np.polyfit(xp, yp, 3))
ax.plot(xp, p3(xp),color='C2')
for (i, t) in zip(NList,invTime):
ax.bar(i, t.average,width=200,color='C0')
ax.errorbar(i, t.average, yerr=t.stdev,color='C1',linewidth=3)
ax.set_xlabel(r'$N$')
ax.set_ylabel('CPU time(s)')
ax.set_xticks(NList)
ax.set_xticklabels(NList)
ax.autoscale(enable=True, axis='y', tight=True)
ax.tick_params(axis ='x', rotation = -45)
ax.legend(['Cubic fit','Average time','Standard Deviations'])
运行后可以得到如下输出
5.46 ms ± 3.93 ms per loop (mean ± std. dev. of 5 runs, 1 loop each)
13.5 ms ± 3.22 ms per loop (mean ± std. dev. of 5 runs, 1 loop each)
50.4 ms ± 6.69 ms per loop (mean ± std. dev. of 5 runs, 1 loop each)
103 ms ± 5.09 ms per loop (mean ± std. dev. of 5 runs, 1 loop each)
186 ms ± 10.8 ms per loop (mean ± std. dev. of 5 runs, 1 loop each)
280 ms ± 34.2 ms per loop (mean ± std. dev. of 5 runs, 1 loop each)
413 ms ± 20 ms per loop (mean ± std. dev. of 5 runs, 1 loop each)
581 ms ± 33.6 ms per loop (mean ± std. dev. of 5 runs, 1 loop each)
877 ms ± 59.7 ms per loop (mean ± std. dev. of 5 runs, 1 loop each)
1.09 s ± 18.9 ms per loop (mean ± std. dev. of 5 runs, 1 loop each)
1.46 s ± 30.2 ms per loop (mean ± std. dev. of 5 runs, 1 loop each)
1.88 s ± 47.5 ms per loop (mean ± std. dev. of 5 runs, 1 loop each)
2.26 s ± 44.4 ms per loop (mean ± std. dev. of 5 runs, 1 loop each)
2.65 s ± 71.2 ms per loop (mean ± std. dev. of 5 runs, 1 loop each)
3.25 s ± 70.7 ms per loop (mean ± std. dev. of 5 runs, 1 loop each)
4.12 s ± 198 ms per loop (mean ± std. dev. of 5 runs, 1 loop each)
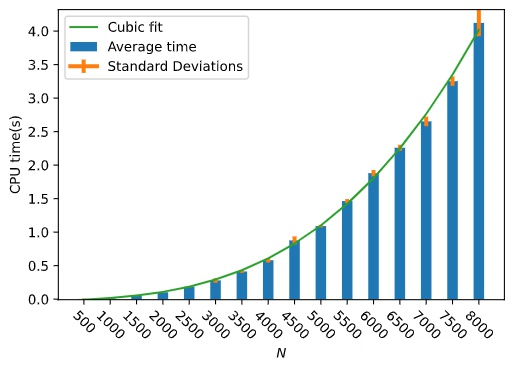
以及下面的图片
从结果的拟合曲线可以看出,求解线性方程组的总体运算时间基本符合 $n$ 的三次方函数。有兴趣的同学也可以试试用二次曲线拟合,看看是否符合。
例子 2:
假设我们的计算机每秒可以处理 $10^9$ 次浮点运算,即 1 giga FLOPS(floating point operations per second),这其实比现在一般的笔记本电脑都要慢得多。下面这个表分别给出的是对于不同尺寸的问题,进行高斯消元运算和只进行向后替换的理论耗时。其中,$t_f$ 是一次浮点运算所需的时间,即 $10^{-9}~\rm{s}$
| 高斯消元 | 后向替换 | |
| $n$ | $2n^3 t_f/3$ | $n^2 t_f$ |
| $10^3$ | $0.67 \,\mathrm{s} $ | $0.001 \,\mathrm{s} $ |
| $10^6$ | $0.67 \times 10^{9} \,\mathrm{s} \approx 21.2 \,\mathrm{years} $ | $1000 \,\mathrm{s} $ |
即使是当今世界上最快的超级计算机,它们的运算速率可以达到 $10^{17}$ FLOPS。如果用高斯消元法求解一个 $n=10^9$ 矩阵,也需要至少 200 年。
然而,很多实际应用问所需要求解的线性方程组的尺度经常会大于 $10^9$,例如一些三维或者更高维度物理过程的模拟仿真,天气预报,等等。那么它们是如何被求解的呢?显然高斯消元只适用于中小尺寸的问题,对于大尺寸的线性方程组,我们需要其他运算复杂度更低的方法进行求解。这个我会在接下来的几期里陆续给大家介绍。