南京理工大学 2008 年 研究生入学考试试题 普通物理(B)
贡献者: 待更新
声明:“该内容来源于网络公开资料,不保证真实性,如有侵权请联系管理员”
1. 填空题(每空 2 分,共 30 分)
1. 一质点作直线运动,运动方程为 $x=3+2t^2+t^3(t>0)\text{(SI 制)}$,则该质点在 $t = 3s$ 时,$v = \underline{\hspace{3cm}}$,在 $t = \underline{\hspace{3cm}}$ 时,质点开始作减速直线运动。
2. 力度系数为 $K$ 的轻弹簧,一端固定,另一端连接一小质量为 $m$ 的物体,$m$ 与地面间的滑动摩擦系数为 $\mu_k$。在弹簧为原长时,对静止物体 $m$ 施一沿 $X$ 轴方向的恒力为 $F (F > f, f = \mu_k mg)$ 时,则该弹簧的最大伸长量为 $\underline{\hspace{3cm}}$,该过程恒力 $\vec{F}$ 作功为 $\underline{\hspace{3cm}}$。
3. 一质量为 $m$,长为 $4r$ 的均匀直尺,一端系于 0 点,另一端连接一质量为 $2m$,半径为 $r$ 的匀质小圆盘边缘。该系统可绕通过 0 点垂直于纸面的轴转动,则该系统对 0 轴的转动惯量 $I = \underline{\hspace{3cm}}$,直尺在水平位置静止并开始转动时的角加速度 $\beta = \underline{\hspace{3cm}}$,直尺转到竖直位置时的角速度 $\omega = \underline{\hspace{3cm}}$。
4. 对于刚性双原子分子理想气体,其定容摩尔热容 $C_v =\underline{\hspace{3cm}}$,等温摩尔热容 $C_T = \underline{\hspace{3cm}}$。
5. $t = 27^\circ C$ 下,$1 \\ mol$ 氧气分子的平均动能为 $\underline{\hspace{3cm}}$;$t = 27^\circ C$ 下,$1 \ mol$ 氧气分子的总动能为 $\underline{\hspace{3cm}}$。
6. 一质点作简谐振动的位移时间曲线如图所示,振幅为 $A$,周期为 $T$,则质点振动的初相角是 $\underline{\hspace{3cm}}$,振动方程为 $\underline{\hspace{3cm}}$。
7.一半径为 $R$ 的导体球的球心为 0 点,在距 0 点 $2R$ 处放置一点电荷,电量为 $q$,则 0 点的电场强度 $E=\underline{\hspace{3cm}}$,电势 $U=\underline{\hspace{3cm}}$。
2. 填空题(每空 2 分,共 30 分)
1. 若一电容器上标明 $200 \\ \text{pF}, \\ 500 \\ \text{V}$,它能储存的最大电能为 $\underline{\hspace{3cm}}$;若该电容器与标明 $300 \\ \text{pF}, \\ 900 \\ \text{V}$ 的另一电容器串联后在两端加 $1000 \\ \text{V}$ 的电压,则此时两电容器的工作状态分别是 $\underline{\hspace{3cm}}$ 和 $\underline{\hspace{3cm}}$。
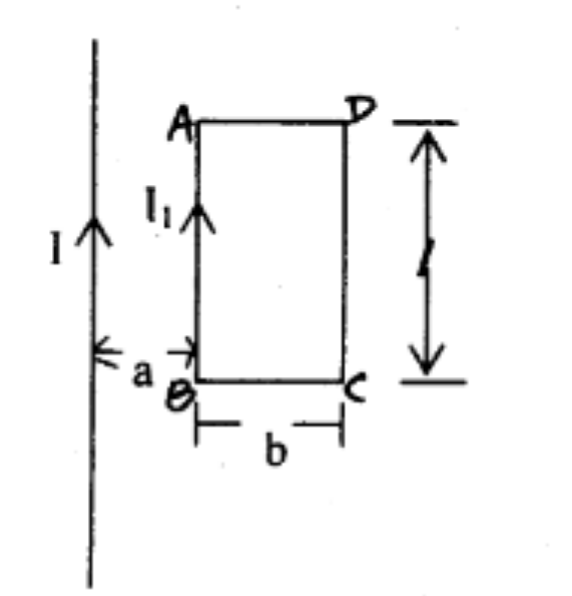
2. 一无限长载流直线 $l$ 与一载流矩形 ABCDA 共面,其尺寸如图所示,则载流线段 $AB$ 受力为 $\underline{\hspace{3cm}}$;载流线段 $BC$ 受力为 $\underline{\hspace{3cm}}$,方向为 $\underline{\hspace{3cm}}$。
3. 油轮泄漏油 $(n = 1.2)$ 入海,在海面上形成一大片油膜,如有人在膜厚为 $4600 \\ \mathring{A}$ 的油膜上空的飞机上垂直往下看,能看到 $\lambda= \underline{\hspace{3cm}}\\ \mathring{A}$ 的光;如有人潜入油膜下方的海里往上看,又能看到 $4 = \underline{\hspace{3cm}}\\ \mathring{A}$ 的光。
4. 一部分偏振光经过一个可旋转的线偏振片后,得到 $I_{\max} / I_{\min} = 3 / 1$,则该部分偏振光中线偏振光的比例为 $\underline{\hspace{3cm}}$;如用自然光通过,则 $I_{\max} / I_{\min} = \underline{\hspace{3cm}}$。
5. 钠的光电效应应允许波长长达 $6250 \\ \mathring{A}$,则钠中电子的逸出功是 $\underline{\hspace{3cm}}$。
6. 电子的静止质量是 $m_0$,当电子以 $v = 0.5c$ 的速度运动时,它的总能量为 $\underline{\hspace{3cm}}$,动能为 $\underline{\hspace{3cm}}$。
7. 在氢原子光谱的巴尔末系中,最短波长为 $\underline{\hspace{3cm}}$,最长波长为 $\underline{\hspace{3cm}}$。
3. (12 分)
已知光栅狭缝的宽度 $a = 1.5 \times 10^{-4} \\, \text{cm}$, 当用波长 $\lambda = 600 \\, \text{nm}$ 的单色光垂直照射在光栅上时,发现第 4 级缺级(第一个缺级),透镜的焦距 $f = 1 \\, \text{m}$,求
(1) 光栅常数;
(2) 屏幕上所呈现的全部明级的级数和条数。
4. (12 分)
一半径为 $R$ 的均匀带电的介质球(介电常数 $\varepsilon$),带电量为 $q$,求
(1) 电场强度分布;
(2) 球内电场能量和球外电场能量之比。
5. (10 分)
试证明:理想气体的定压摩尔热容量为 $C_p = \frac{i + 2}{2} R$,$R$ 为普适气体常量。
6. (10 分)
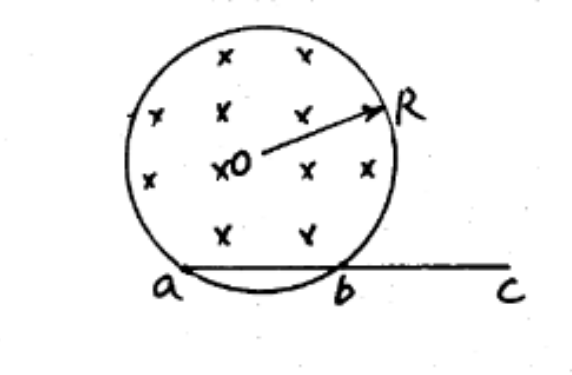
无限长螺线管半径为 $R$,管内磁场的变化率 $\frac{dB}{dt} = k (k < 0)$,导体棒 $ab = bc = R$,试求导体棒中感应电动势的大小和方向。
7. (12 分)
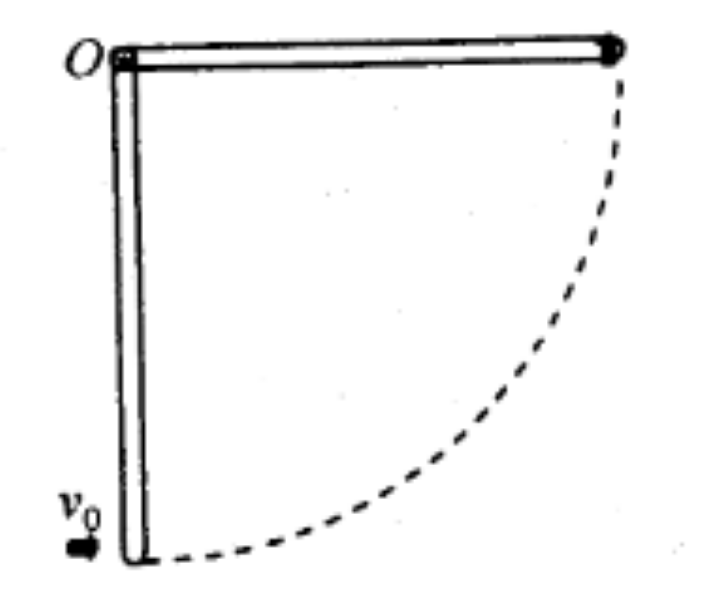
如图所示,一均匀直棒长度为 \( l \),质量为 \( M \),上端挂在水平轴 0 上,自由下垂。今有一质量为 \( m \) 的子弹水平射入杆下端而不复出,以后棒摆至水平位置又开始下落,设子弹射入到停止在棒内均极短,空气阻力不计。求子弹进入棒前的速度。
8. (12 分)
同一媒质中的两波源 A、B,相距为 \( AB=30m \),它们的振幅相同,频率都是 100Hz,相位差为 \( \pi \),波速为 \( 400m \cdot s^{-1} \),试求 A、B 连线上的干涉而静止的各点的位置,而 \(A,B\) 外侧各点的振动情况如何?
9. (10 分)
一根长直圆柱形 (半径为 \( R\)) 导线载有电流 \( I \),均匀地分布在它的横截面上。求这导线内部单位长度的磁场能量。
10. (12 分)
具有能量为 15ev 的光子,被氢原子中处于第一波尔轨道的电子所吸收而形成一光电子。问此光电子远离原子时速度多大?它的德布罗意波长是多少?
附:电子静止质量 \( m_0=9.1 \times 10^{-31} \) (Kg)
电子电量 \( e=1.6 \times 10^{-19} \) (C)
普朗克常数 \( h=6.63 \times 10^{-34} \) (J \cdot s)
玻尔兹曼常数 \( k=1.38 \times 10^{-23} \) (J/K)
真空电容率 \( \epsilon_0=8.85 \times 10^{-12} C^2/N \cdot m^2 \)
真空中光速 \( c=3 \times 10^8 \) (m/s)
普适气体恒量 \( R=8.31 \) (J/mol \cdot K)