南京理工大学 2004 年 研究生入学考试试题 普通物理(B)
贡献者: 待更新
声明:“该内容来源于网络公开资料,不保证真实性,如有侵权请联系管理员”
1. 填空题(每空 2 分,总共 32 分)
1. 已知质点作半径为 \( R \) 的匀加速率圆周运动,其角位置 \( \theta = \theta_0 + \omega_0 t + bt^2/2 \),其中 \( \theta_0 \), \( \omega_0 \), \( b \) 均为常数,则质点在 \( t \) 时刻的速率为 $\underline{\hspace{2cm}}$,\( t \) 时刻的法向加速度大小为 $\underline{\hspace{2cm}}$,\( t \) 时刻的切向加速度大小为 $\underline{\hspace{2cm}}$。
2. 已知一质点作简谐振动,其振动方程为 \( y = 0.1 \cos\left(100\pi t + \pi/3\right) \) (米),则 \( t = 1 \) 秒时质点的振动速度大小为 $\underline{\hspace{2cm}}$ 米/秒,振动加速度大小为 $\underline{\hspace{2cm}}$ 米/秒 \(^2\)。
3. 已知一沿 $ +x $ 方向传播的简谐波的波动方程为 $y = 0.05 \cos\left(100\pi t - 20x + \pi/3\right) $ (米)。则该简谐波的传播速度为 $\underline{\hspace{2cm}}$,波长为 $\underline{\hspace{2cm}}$ 在波线上同一时刻相位差为 $\pi/3$ 的两点间的距离为 $\underline{\hspace{2cm}}$
4.一半径为 $R$ 的金属球,带电 $Q$,则球中心 0 点的电场强度为 $\underline{\hspace{2cm}}$,其电势为球内任一点的电势为 $\underline{\hspace{2cm}}$。
5.一半径为 $R$ 的圆环状载流回路,由 $N$ 匝线圈组成,设一匝线中通过电流 $I$,则圆环中圆环铀线上距圆环中心 $x$ 心处的磁感应强度大小为 $\underline{\hspace{2cm}}$,方向为 $\underline{\hspace{2cm}}$,处的磁感应强度大小为 $\underline{\hspace{2cm}}$。
6.写出磁场中高斯定理的数学表达式 $\underline{\hspace{2cm}}$,它说明磁场足 $\underline{\hspace{2cm}}$。
2. 填空题(每空 2 分,总共 28 分)
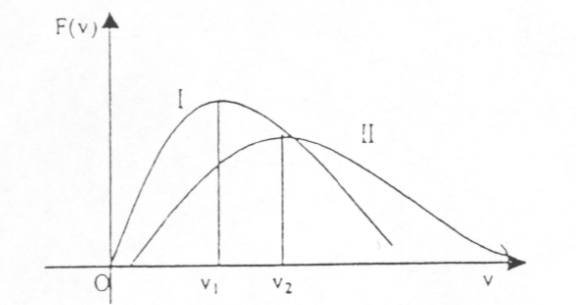
1.如图,曲线 $I$ 表示 27℃的氧气分子的 Maxwell 速率分布,则图示中 $v_1=\underline{\hspace{2cm}}$,Ⅱ也表示氧气分子某一温度下的 Maxwell 速率分布,且 $v_2=600m/s$,则曲线Ⅱ对应的氧气的理想气体温标 $T_2=\underline{\hspace{2cm}}$
2.一理想气体经历一次卡诺循环对外做功 $1000J$,卡诺循环高温热源温度 $T_1=500K$,低混热源温度 $T_2=300K$,则在一次循环中,内能增量为,在高温热源处吸热 $Q=\underline{\hspace{2cm}}$ 在低温热源处放热 $Q_2=\underline{\hspace{2cm}}$。
3.一长度为 $L$ 平饭洪璃片,一端相连,另一端有一个直径为 $d$ 的细丝夹住,利用波长为 $\lambda$ 的单色平行光垂直照射,则平板波璃片上的干涉条纹间距为 $\underline{\hspace{2cm}}$,若把细丝另一端移动,则条纹向 $\underline{\hspace{2cm}}$ 移动,条纹间距变 $\underline{\hspace{2cm}}$。
4.爱因斯坦狭义相对论的两条基本假说是 $\underline{\hspace{2cm}}$,绝对黑体的单色吸收比是 $\underline{\hspace{2cm}}$,测不准关系表达式是 $\underline{\hspace{2cm}}$。
5.一屯子以 $0.6c$ 的速度运动,则该电子的运动质量为 $\underline{\hspace{2cm}}$,该电子的动能等于 $\underline{\hspace{2cm}}$,若该电子从 $0.6c$ 的速度被加速到 $0.8c$,外力需做功 $\underline{\hspace{2cm}}$。
3. 三、10 分
一劲度系数为 $k$ 的轻弹簧水平放置,一端固定,另一端连接一质量为 $m$ 的物体,$m$ 与地面间的滑动摩拣系数为 $\mu$;在弹簧为原长时,对静止物体施一沿 $x$ 正方向的恒力 F($F>f,f$,为摩擦力的大小),试求弹簧的最大伸长量。
4. 四、10 分
一质量为 $m$、半径为 $R$ 的定滑轮(可看作均匀薄圆盘),可绕垂直于纸面的水平光滑轴 0 无摩擦地转动,轮緣绕一细轻绳,绳下端挂一质量为 $m_2$ 的物体,物体从静止开始下降,设绳与滑轮之间不打滑,求任一时刻 $t$ 物体下降的速度。
5. 五、12 分
画出卡诺正循环示意图,做简要说明,并证明理想气体卡诺正循环热机效串 $\eta=1-T_2/T_1$,$T_1$ 为高温热源温度,$T_2$ 为低温热源温度。
6. 六、12 分
一半径为 $R$、均匀带电 $q$ 的圆环的中心为 0 点,求(1)圆环轴线上距 0 点 $x$ 距离的 $P$ 点与 0 点之间的电势差,(2)$P$ 点的电场强度。
7. 七、10 分
一内外半径分别为 $R_1,R_2$ 的无限长圆筒,载有电流为 $I$,求圆筒内外的磁感应强度分布。
8. 八、12 分
用波长为 $632.8nm$ 的单色光垂直照射一每厘米 1250 条刻痕的光栅,刻痕宽度与狭缝宽度相等,求(1)最多能看到第几级?(2)总共能看到多少条谱线。
9. 九、12 分
钠黄光 $\lambda=589.3nm$ 照射某光电池时,为截止所有光电子到达阳极,需加 $0.3V$ 的反向电压。如果用 $\lambda=400nm$ 的光照射这个光电池,则需多大反向电压才能截止所有光电子到达阳极。
10. 十、12 分
求经 20 万伏的电压加速的电子的动能、运动速度大小、德布罗意物质波长。
附物理常数:
电子质量 $m_e = 9.11 \times 10^{-31} \\, \text{千克}$,
电子电量 $e = 1.6 \times 10^{-19} \\, \text{库仑}$,
普朗克常数 $h = 6.63 \times 10^{-34} \\, \text{焦耳·秒}$,
真空中光速 $c = 3 \times 10^8 \\, \text{米/秒}$.