南京理工大学 2005 年 研究生入学考试试题 普通物理（B）

                     

贡献者： 待更新

　　 声明：“该内容来源于网络公开资料，不保证真实性，如有侵权请联系管理员”

1. 一、填空题（26 分，每题 2 分）

　　 1. 一质点作平面运动，运动方程为 $r=6ti+5t^2j$，则 $t$ 时刻质点的速度为__________，加速度为______。

　　 2. 一均质细棒，长为 $L$，质量为 $m$，一端固定于 $O$ 点，棒可绕 $O$ 点转动。开始时托住 $B$ 端让棒处在水平位置，然后松手，则棒处在水平位置时的角加速度大小为___________，棒到达竖直位置时的角加速度为_______，转动动能为___________。

　　 3. 27°C 的 $1mol$ 氧气分子的最概然速率为____________，其物理意义为__________，分子的平均平动动能为_________，$1mol$ 理想氧气的内能为________。

　　 4. 以波速 $u$ 向 $X$ 正方向传播的平面简谐波，振幅为 $A$，圆频率为 $\omega$，设位于坐标 $x_0$ 处的质点，$t=0$ 时，位移 $y=A/2$，且向 $y$ 负方向运动，则该质点的振动方程为__________，该平面简谐波的波动方程（波函数）为___________。 5.一平面简谐波方程(波函数)为 $y_1=4\cos2\pi(\frac{t}{T}+\frac{x}{\lambda})$,在 $x=\frac{\lambda}{2}$-一处有一反射壁若平面波从空气传到反射壁而反射，反射时振幅不变，已知空气为波疏介质，则反射波波动方程为__________，波节点的位置为___________。

2. 二、填空题（28 分，每空 2 分）

　　 1.一无限长均匀带电直线，电荷线密度为 $\lambda$，则离直线距离为 $r$ 处电场强度大小为__________，距直线距离为 $r_a$ 和 $r_b(r_b>r_a)$ 的两点间的电势差 $\varphi_a-\varphi_b$__________。

　　 2.一个电矩为 $p=q$ 的电偶极子轴线(即沿着的方向)距其中心为 $r(r>>1)$ 处的一点的场强(用 $r$ 和 $p$ 表示)为__________。

　　 3.若氢原子中电子(电量为 $e$)在一半径为 R 的圆轨道上以速率 v 作匀速率圆周运动，则圆心处的磁感应强度大小为__________，圆心处的磁场能量密度为__________。

　　 4.白然光入射到空气和某玻璃的分界面上，当入射角为 60°时，反射光为完全偏振光，则该玻璃的折射率为__________，一束强度为 $I0$ 的自然光垂直入射于两块平行放置且透光轴方向夹角为 60。的偏振光上，则透射光的强度为__________。

　　 5.用氦一氖激光器发出的波长为 $632.8nm$ 的单色光做牛顿环实验，测得第 k 级暗环的半径为 $5.625mm$，第 $k+5$ 级暗环的半径为 7.956nm，，则所用平凸透镜的曲率半径 $R=$__________，$k=$__________。

　　 6. S 系中一质量为 $m0$、体积为 $V0$ 的立方体，若使此立方体沿平行于一边的方向以速度 $v=0.6c$ 运动，则在 $S$ 系中测得其体积为____________，动能为________。

　　 7. 基态氢原子中的电子吸收一个能量为 $12eV$ 的光子后所能到达的最高能态为__ ________，从该能态直接跃迁回基态辐射的光子频率为__________。

　　 5.已知一维无限深势阱中粒子的波函数为:$\psi_n(x)=\sqrt{\frac{2}{a}}\sin\frac{n\pi}{a}x$,则 $n=2$ 时，粒子在 $x=\frac{a}{2}$ 处出现的概率密度为__________。

3. 三、（12 分）

　　 质量为 $m$ 的小球在光滑的水平面内沿半径为 $R$ 的固定圆环作圆周运动。已知小球与圆环间的滑动摩擦系数为 $\mu k$，小球的初速度大小为 $v0$，求小球运动三周回到原来位置时的速度大小。

4. 四、（12 分）

　　 已知轻弹簧的劲度系数为 $k$，定滑轮可看作质量为 $M$、半径为 $R$ 的均质圆盘，物体的质量为 $m$，试求：（1）系统的振动周期；（2）当将 $m$ 托至弹簧原长并释放时，求 $m$ 的运动方程（以向下为正方向）。

5. 五、（12 分）

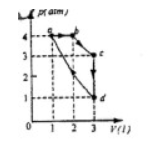
　　 1 摩尔单原子分子组成的理想气体系统，经如右图所示的循环过程，求：（1）一个循环中，系统对外做的功；（2）循环效率

6. 六、（12 分）

　　 内外半径分别为 $R1,R2$ 的金属球壳中心处放置一点电荷 $q$，金属球壳带电 $Q$，试求：（1）电场强度的分布；（2）金属球壳的电势（设无穷远处为零电势点）。

7. 七、（12 分）

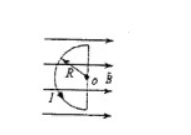
　　 一个半径 $R=0.18m$ 的半圆形闭合线圈，载有电流 $I=10A$，放在 $B=10T$ 的均匀外磁场中，磁场方向与线圈平面平行，如图所示，求：（1）线圈磁矩的大小与方向；（2）线圈所受磁力矩的大小与方向。（3）在磁力矩的作用下，线圈平面绕纸面内过 $O$ 点的竖直轴转过 $\pi/2$ 时，磁力矩作的功（设 $I$ 在旋转过程中不变）

8. 八、（12 分）

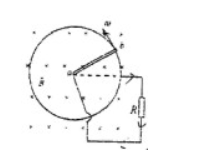
　　 磁感应强度为 $B$ 的均匀磁场垂直纸面向内，一长度为 $L$ 的金属杆 $ab$ 以 $a$ 为中心、角速度为 $w$ 旋转，$b$ 在半径为 $L$ 的金属圆环上滑动，接触良好，旋转中心与金属环之间接一电阻 $R$，求：（1）$ab$ 杆上动生电动势的大小与方向；（2）$ab$ 杆受到的磁力矩。

9. 九、（12 分）

　　 波长为 $450nm$ 的单色光垂直入射在一光栅上，第二级明纹出现在衍射角的正弦等于 0.3 处，第三级为第一个缺级。求：（1）光栅常数；（2）通光狭缝的宽度 $a$；（3）屏上可观察到的明纹数及其级数。

10. 十、（12 分）

　　 试计算：
（1）经 $200V$ 的电势差加速后的电子的德布罗意波长；
（2）动能为 $1.38MeV$ 的电子的德布罗意波长。