洛伦兹吸引子

贡献者： shizy0808; addis

预备知识　四阶龙格库塔法

1. 洛伦兹方程

　　¹20 世纪 60 年代，蓬勃发展的计算机技术开始得到广泛应用，其中包括长期天气预报。大气与液体同属流体，太阳照射使地面升温，靠近地面的气体受到加热，而高层大气还是冷的，于是上、下层气体之间将会出现对流，产生类似于贝纳德实验中的对流现象。在美国气象局工作的数学家洛伦兹（E.N. Lorenz）将大气对流与贝纳德液体对流联系起来，企图用数值方法进行长期天气预报。从贝纳德对流出发，利用流体力学中的纳维叶-斯托克斯（Navier-Stokes）方程、热传导方程和连续性方程，洛伦兹推导出了描述大气对流的微分方程

\begin{align} & \frac{\mathrm{d}{x}}{\mathrm{d}{t}} =-\sigma (x-y)~,\\ & \frac{\mathrm{d}{y}}{\mathrm{d}{t}} =rx-y-xz~,\\ & \frac{\mathrm{d}{z}}{\mathrm{d}{t}} =-bz+xy~. \end{align}

式子中，$r$ 是对流的翻动速率; $y$ 正比于上流与下流液体之间的温差;$z$ 是垂直方向的温度梯度; $\sigma$ 为无量纲因子，称为 Prandtl 数; $b$ 为反映速度阻尼的常数。其中，$xz$ 与 $xy$ 是非线性项。

　　洛伦兹方程是一个能量耗散系统，这可以从它的相空间随时间变化的特性来证明。设在 $(x,y, z)$ 三维相空间取一个闭合曲面，该曲面所包围的体积 $V$ 随时间的变化为：

\begin{align} \frac{\mathrm{d}{V}}{\mathrm{d}{t}} =\int_V \Big( \frac{\mathrm{d}{\dot{x}}}{\mathrm{d}{t}} + \frac{\mathrm{d}{\dot{y}}}{\mathrm{d}{t}} + \frac{\mathrm{d}{\dot{z}}}{\mathrm{d}{t}} \Big)~, \end{align}

式中，$ \,\mathrm{d}{\dot{x}} $, $d\dot{y}$, $d\dot{z}$ 为代表点在相空间的相应方向上的运动速度。由洛伦兹方程得

\begin{align} & \frac{\mathrm{d}{\dot{x}}}{\mathrm{d}{t}} =-\sigma~,\\ & \frac{\mathrm{d}{\dot{y}}}{\mathrm{d}{t}} =-1~,\\ & \frac{\mathrm{d}{\dot{z}}}{\mathrm{d}{t}} =-b~, \end{align}

于是，就有

\begin{align} \frac{\mathrm{d}{V}}{\mathrm{d}{t}} =-(\sigma+1+b)V~. \end{align}

解此方程得到

\begin{align} V(t)=V_0 \exp\left[-(\sigma+1+b)t\right] ~, \end{align}

式中，$V_0$ 为初始相空间的体积。由于参数 $b>0,\sigma>0$,可见洛伦兹方程的相空间体积 $V(t)$ 是随时间收缩的，由初始时的有限相体积 $V_0$ 随时间收缩到一点，这一点应是坐标系的原点 $x=y=z=0$.由此可见，洛伦兹方程描述的是一个耗散系统。正如阻尼单摆那样，耗散意味着系统存在吸引子。

2. 洛伦兹方程解的分岔

　　由 $\dot{x}=\dot{y}=\dot{z}=0$ 可得洛伦兹方程的三个平衡点：

\begin{align} x=y=z=0~,\qquad x=y=\pm\sqrt{b(r-1)}~, z=r-1~. \end{align}

然而，如果 $r<1$,后两个平衡点就不存在，只存在 $x=y=z=0$ 这个平衡点。因此，平衡点 $x=y=z=0$ 是洛伦兹方程的不动点，相应于贝纳德实验中液体的静止定态。为了研究平衡点的稳定性问题，我们将方程写成矩阵形式

\begin{align} \left(\begin{array}{l} \dot{x} \\ \dot{y} \\ \dot{z} \end{array}\right)=\left(\begin{array}{ccc} -\sigma & \sigma & 0 \\ r-z & -1 & -x \\ y & x & -b \end{array}\right)\left(\begin{array}{l} x \\ y \\ z \end{array}\right)~. \end{align}

首先讨论坐标原点 $x=y=z=0$ 的稳定性。为此，对原点的邻域作线性化处理，即

\begin{align} \left(\begin{array}{l} \dot{x}_{0} \\ \dot{y}_{0} \\ \dot{z}_{0} \end{array}\right)=\left(\begin{array}{ccc} -\sigma & \sigma & 0 \\ r & -1 & 0 \\ 0 & 0 & -b \end{array}\right)\left(\begin{array}{l} x_{0} \\ y_{0} \\ z_{0} \end{array}\right)~. \end{align}

线性方程系数矩阵本征值为

\begin{align} \lambda_{1.2}=\frac{1}{2}\left[-(\sigma+1) \pm \sqrt{(\sigma-1)^{2}+4 \sigma r}\right]~, \quad \lambda_{3}=-b~. \end{align}

通常把参数 $\sigma$ 和 $b$ 固定为 $10$ 和 $8/3$,研究随着 $r$ 的变化，系统的动力学行为是如何变化的。

3. 吸引子

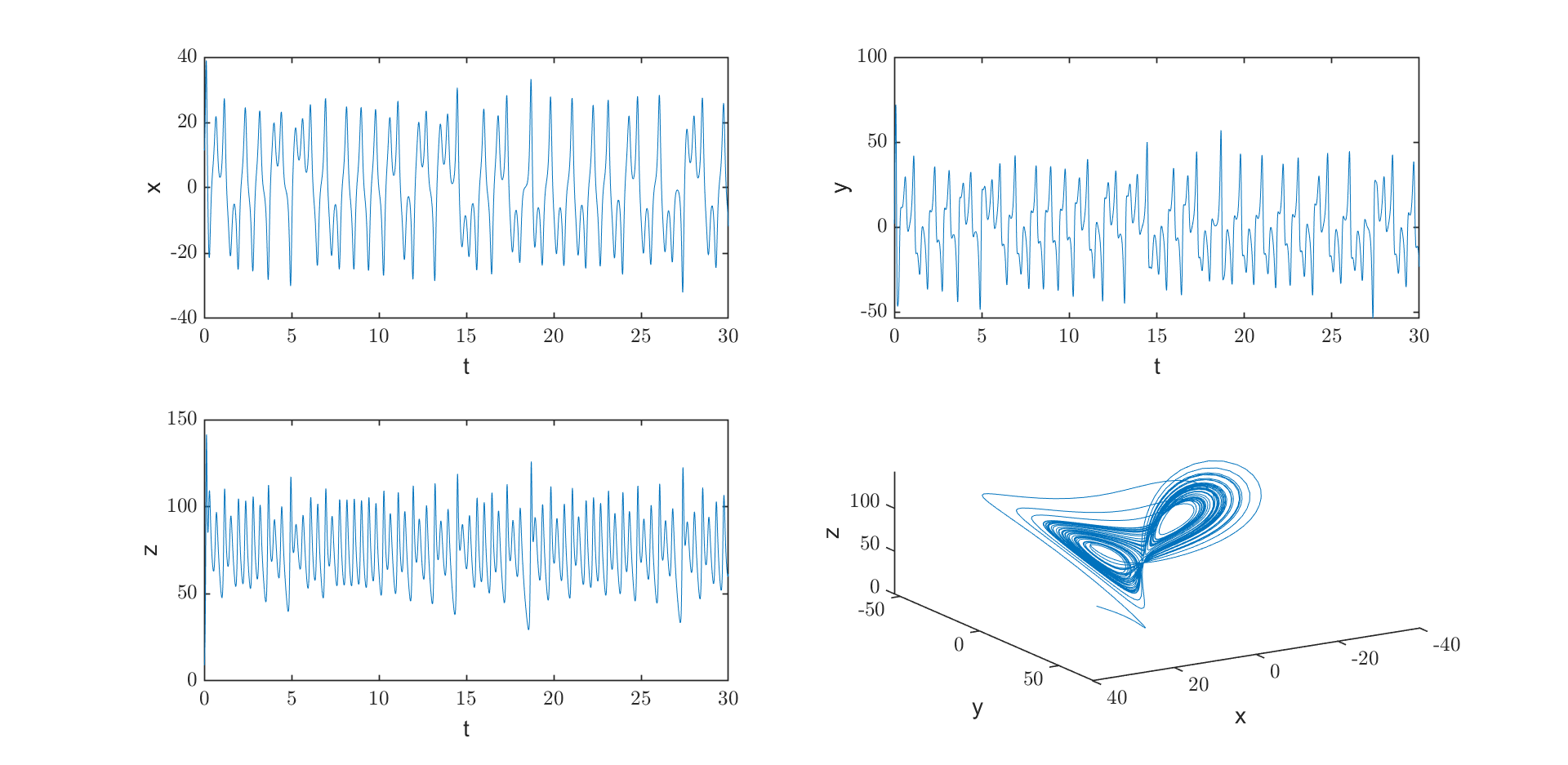
　　由于洛伦兹方程混沌的特点，即对初值非常敏感。如今，这一方程组已成为混沌理论的经典，也是 “巴西蝴蝶扇动翅膀在美国引起德克萨斯的飓风” 一说的肇始。下面几幅图给出了初值稍微变化一点点最终导致完全不同的动力学轨迹的图像。

图 1：吸引子. 参数取值 $\sigma=10,b=8/3, r=80$. 初始条件：$(x_0,y_0,z_0)=(12,2,9)$

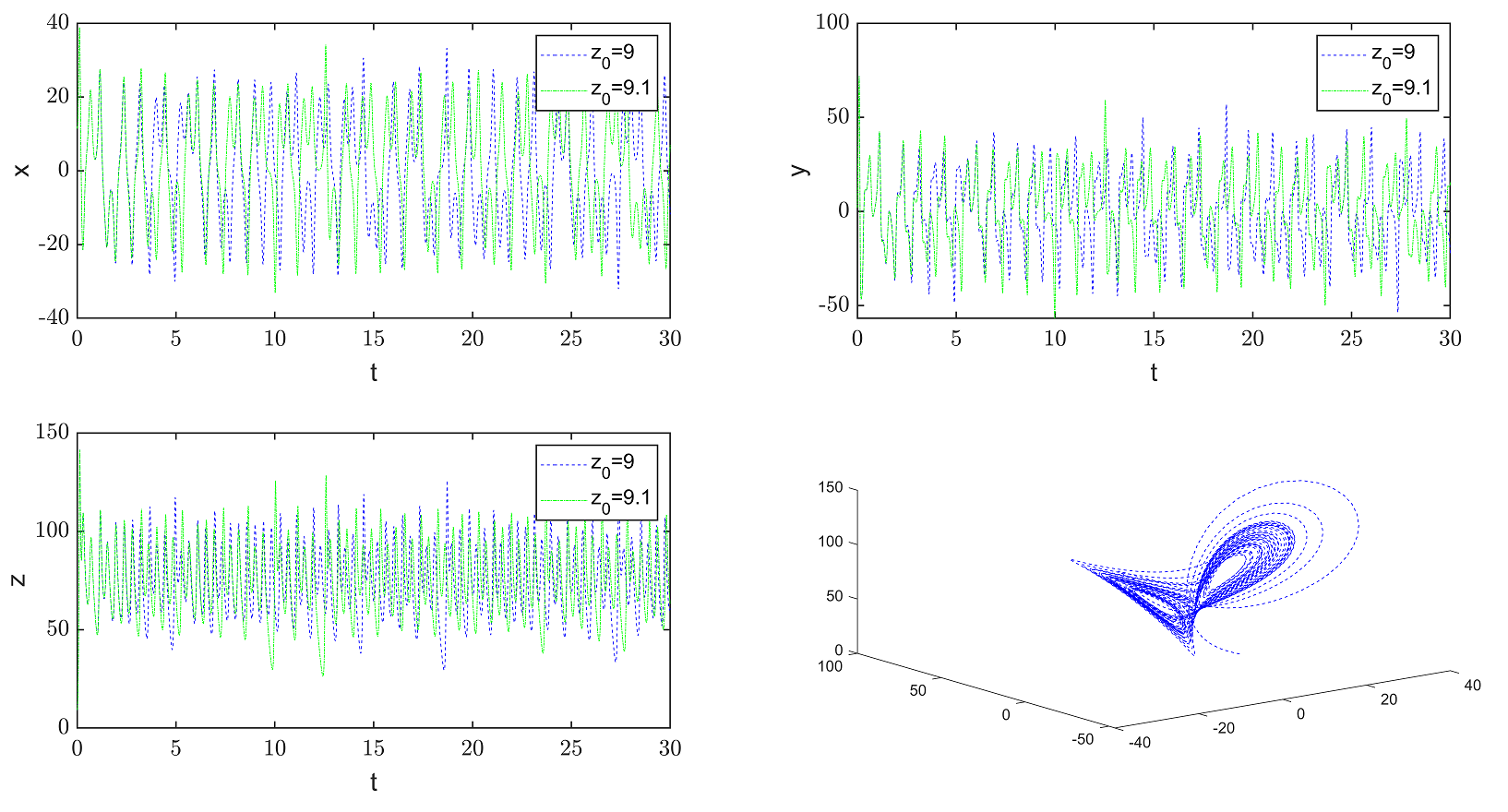
图 2：吸引子. 参数取值 $\sigma=10,b=8/3, r=80$. 初始条件：蓝线 $(x_0,y_0,z_0)=(12,2,9)$ 以及红线 $(x_0,y_0,z_0)=(12,2,9).1$。

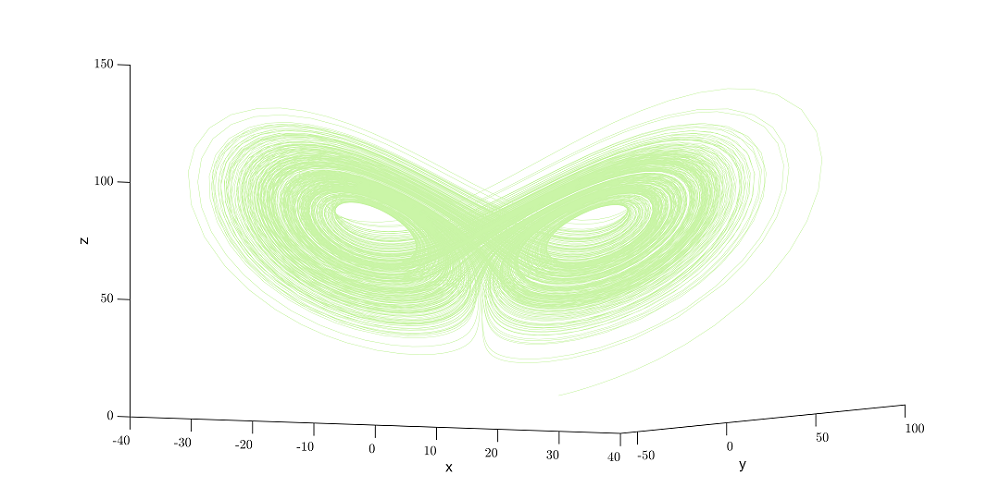
图 3：三维吸引子。

代码 1：lorenz.m

clear all
clc
clf
r = 80;
[t,y]=ode45(@Lorenz,[0,30],[12,2,9],[],r);
[t1,y1]=ode45(@Lorenz,[0,30],[12,2,9.1],[],r);

subplot(221);
plot(t,y(:,1),'b--');
hold on
plot(t1,y1(:,1),'g-.');
legend('z_0=9', 'z_0=9.1')

xlabel('t')
ylabel('x')
set(gca,'linewidth',1,'fontsize',15,'TickLabelInterpreter','latex')
subplot(222);
plot(t,y(:,2),'b--');
hold on
plot(t1,y1(:,2),'g-.');
legend('z_0=9', 'z_0=9.1')

xlabel('t')
ylabel('y')
set(gca,'linewidth',1,'fontsize',15,'TickLabelInterpreter','latex')

subplot(223);
plot(t,y(:,3),'b--');
hold on
plot(t1,y1(:,3),'g-.');
legend('z_0=9', 'z_0=9.1')

xlabel('t')
ylabel('z')
set(gca,'linewidth',1,'fontsize',15,'TickLabelInterpreter','latex')

subplot(224);
plot3(y(:,1),y(:,2),y(:,3),'b--');
hold on
plot3(y1(:,1),y2(:,2),y3(:,3),'g-.');
legend('z_0=9', 'z_0=9.1')

view([45 42]);
xlabel('x')
ylabel('y')
zlabel('z')
set(gca,'linewidth',1,'fontsize',15,'TickLabelInterpreter','latex')

function dy=Lorenz(t,y,r) %
    dy=zeros(3,1);
    dy(1)=10*(-y(1)+y(2));
    dy(2)=r*y(1)-y(2)-y(1)*y(3);
    dy(3)=y(1)*y(2)-8*y(3)/3;
    
end

1. ^ 参考 Wikipedia 相关页面。