木块堆叠问题(里拉斜塔)
贡献者: addis
- 本文处于草稿阶段。
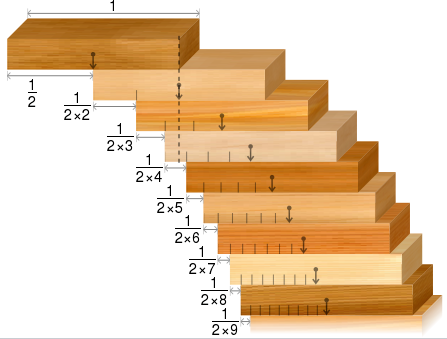
1木块推叠问题也称为里拉斜塔,如图 1 所示。如何对方可以使最顶端的木块伸出最多。
可以证明从上到下第 $n$ 块($n=1,2,\dots$)最多可以伸出的长度为 $Ln/2$。故 $N$ 个木块最多伸出的总长度为
\begin{equation}
d_N = \frac{L}{2} \left(1 + \frac{1}{2} + \frac{1}{3} + \dots + \frac{1}{N} \right) ~.
\end{equation}
图 1:里拉斜塔(来自 Wikipedia)
1. 推导
我们先来证明, 可以用递归法证明。 一个关键的思路在于,上方 $n$ 个木块看成一个整体,然后在下方添加一个木块后,$L/2$ 长度的两端质量比例为 $n:1$,所以质心位置应该在 $1/(n+1)$ 处。
这里用到一个定理:两个质点系的质心位置就是两个质点系各自的质心的质心,见子节 3 。