线性回归

贡献者： lrqlrqlrq; xzllxls

预备知识　函数（高中），几何矢量的内积，回归

　　 线性回归（Linear regression）是一种利用线性函数对自变量（特征）和因变量之间的关系进行建模的方法。线性回归是机器学习中一种广泛使用的基本回归算法。含有有多个特征的线性回归称为多元线性回归。

　　假设有 $n$ 个特征（自变量）$x_1$,$x_2$,...,$x_n$，一个输出变量 $y$，线性回归的一般形式表示如下：

\begin{equation} y=f( \boldsymbol{\mathbf{x}} )=w_1x_1+w_2x_2+...+w_nx_n+b~. \end{equation}

其中，系数 $w_1$,$w_2$,...,$w_n$ 为特征的权重，$b$ 为偏置。上式也可以写成向量的形式：

\begin{equation} y=f( \boldsymbol{\mathbf{x}} )= \boldsymbol{\mathbf{w}} ^T \boldsymbol{\mathbf{x}} +b~. \end{equation}

其中，$ \boldsymbol{\mathbf{x}} = [x_1,x_2,...,x_n]$,$ \boldsymbol{\mathbf{w}} = [w_1,w_2,...,w_n]$.

　　 模型参数： 在线性回归中，模型的参数包括权重向量 $\mathbf{w}$ 和偏置 $b$。这些参数通过学习算法进行调整，以使模型尽可能准确地拟合训练数据。

　　 训练过程： 线性回归的训练过程旨在找到最佳的权重和偏置，以最小化预测值与实际值之间的差距。常用的方法包括最小二乘法和梯度下降法。

1. python 具体的实现

　　下面是线性回归的简单实现代码，使用了 Python 中的 NumPy 库：

import numpy as np

class LinearRegression:
    def __init__(self):
        self.weights = None
        self.bias = None

    def fit(self, X, y):
        # 添加偏置项
        X_b = np.c_[np.ones((X.shape[0], 1)), X]
        # 使用最小二乘法计算权重
        self.weights = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)
        
    def predict(self, X):
        # 添加偏置项
        X_b = np.c_[np.ones((X.shape[0], 1)), X]
        # 计算预测值
        return X_b.dot(self.weights)

　　接下来我们生成一些随机数据，用这些数据去训练模型，然后用训练后的模型去做预测，最后可视化拟合结果。

import matplotlib.pyplot as plt

# 生成随机数据
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)

# 定义模型
model = LinearRegression()

# 训练模型
model.fit(X, y)

# 预测
y_pred = model.predict(X)

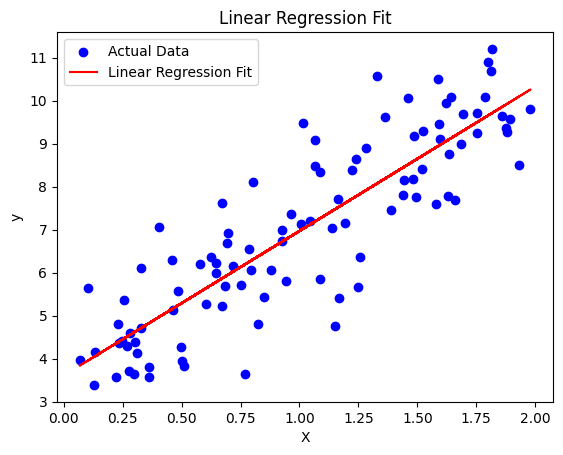
# 可视化拟合结果
plt.scatter(X, y, color='blue', label='Actual Data')
plt.plot(X, y_pred, color='red', label='Linear Regression Fit')
plt.title('Linear Regression Fit')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.show()

图 1：线性回归

2. 进阶的数学原理

　　不难看出，上面的代码真正的核心内容只有一段：

np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y) # 使用最小二乘法计算权重

　　接下来，我们就要用严谨的数学去论证和解释为什么这段简短的代码，能够找到最优的线性拟合函数。

　　 最小二乘法（Least Squares Method）：

　　最小二乘法是一种用于拟合线性模型的常见方法，其目标是通过最小化残差平方和来找到最佳拟合线。在线性回归中，最小二乘法的目标是使预测值与实际值的残差的平方和最小化。

　　对于线性回归的模型 $y = \mathbf{w}^T \mathbf{x} + b$，最小二乘法的优化目标是最小化损失函数：

\begin{equation} L(\mathbf{w}, b) = \sum_{i=1}^{m} (y^{(i)} - (\mathbf{w}^T \mathbf{x}^{(i)} + b))^2~. \end{equation}

　　其中，$m$ 是训练样本数，$\mathbf{x}^{(i)}$ 是第 $i$ 个样本的特征向量，$y^{(i)}$ 是实际输出值。

　　通过对损失函数对参数 $\mathbf{w}$ 和 $b$ 求偏导数，并令其等于零，可以得到最小二乘法的闭式解，即正规方程。

　　 正规方程（Normal Equation）：

　　正规方程是通过对损失函数的偏导数等于零来求解线性回归模型参数的解析解。对于线性回归的损失函数，其正规方程可以写为以下形式：

\begin{equation} \mathbf{w} = (\mathbf{X}^T \mathbf{X})^{-1} \mathbf{X}^T \mathbf{y}~. \end{equation}

这就是我们之前的核心代码。其中，$\mathbf{X}$ 是包含所有训练样本特征的矩阵，$\mathbf{y}$ 是实际输出值的向量。

　　正规方程的求解涉及矩阵的求逆运算，因此当特征矩阵 $\mathbf{X}^T \mathbf{X}$ 可逆时，可以得到唯一解。但在实际应用中，特征矩阵可能不可逆，或者矩阵求逆的计算代价较高。在这些情况下，可以考虑使用其他优化算法，如梯度下降法，来求解模型参数。后面也会有文章讲伪逆（Moore-Penrose pseudo-inverse）。

　　正规方程的优点是能够直接得到参数的解析解，但在大规模数据集上计算矩阵逆的代价较高，因此在实际应用中需要权衡选择最适合问题的方法。

例 1　详细过程：通过对损失函数对参数 $\mathbf{w}$ 和 $b$ 求偏导数，并令其等于零，来求解最小二乘法的闭式解。

　　对 $\mathbf{w}$ 求偏导数：

\begin{equation} \frac{\partial L}{\partial \mathbf{w}} = -2 \sum_{i=1}^{m} \mathbf{x}^{(i)} (y^{(i)} - (\mathbf{w}^T \mathbf{x}^{(i)} + b))~. \end{equation}

将上式置零，得到：

\begin{equation} \sum_{i=1}^{m} \mathbf{x}^{(i)} (\mathbf{w}^T \mathbf{x}^{(i)} + b) = \sum_{i=1}^{m} \mathbf{x}^{(i)} y^{(i)}~. \end{equation}

这可以写成矩阵形式：

\begin{equation} \mathbf{X}^T (\mathbf{X} \mathbf{w} + b\mathbf{1}) = \mathbf{X}^T \mathbf{y}~. \end{equation}

　　其中，$\mathbf{X}$ 是包含所有训练样本特征的矩阵，$\mathbf{1}$ 是全 1 向量。

　　对 $b$ 求偏导数：

\begin{equation} \frac{\partial L}{\partial b} = -2 \sum_{i=1}^{m} (y^{(i)} - (\mathbf{w}^T \mathbf{x}^{(i)} + b))~. \end{equation}

将上式置零，得到：

\begin{equation} \sum_{i=1}^{m} (y^{(i)} - (\mathbf{w}^T \mathbf{x}^{(i)} + b)) = 0~. \end{equation}

化简后得到：

\begin{equation} \sum_{i=1}^{m} y^{(i)} = \sum_{i=1}^{m} (\mathbf{w}^T \mathbf{x}^{(i)} + b)~. \end{equation}

将上述两个方程与矩阵形式相结合，得到正规方程：

\begin{equation} \begin{bmatrix} \mathbf{X}^T \mathbf{X} & \mathbf{X}^T \mathbf{1} \\ \mathbf{1}^T \mathbf{X} & m \end{bmatrix} \begin{bmatrix} \mathbf{w} \\ b \end{bmatrix} = \begin{bmatrix} \mathbf{X}^T \mathbf{y} \\ \sum_{i=1}^{m} y^{(i)} \end{bmatrix}~. \end{equation}

解这个方程，就能得到最小二乘法的闭式解：

\begin{equation} \begin{bmatrix} \mathbf{w} \\ b \end{bmatrix} = \begin{bmatrix} (\mathbf{X}^T \mathbf{X})^{-1} \mathbf{X}^T \mathbf{y} \\ \frac{1}{m} \sum_{i=1}^{m} y^{(i)} \end{bmatrix}~. \end{equation}

这就是使用最小二乘法得到线性回归模型的闭式解的详细步骤。在实际应用中，通过求解正规方程，可以直接得到参数的解析解，但需要注意矩阵 $\mathbf{X}^T \mathbf{X}$ 可逆的情况。

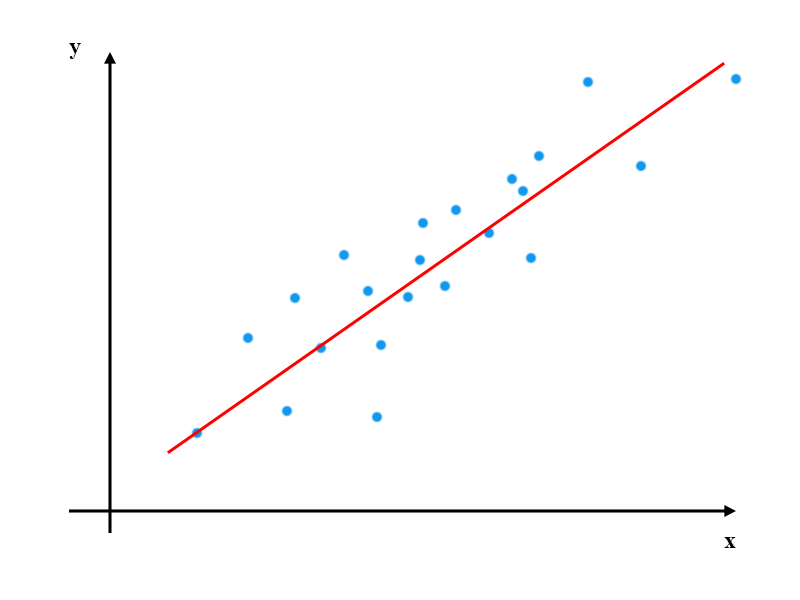
　　一个一元线性回归的示意图如下：

图 2：示意图

　　图中，蓝色表示数据点，红色直线表示最终求得的线性回归结果。

　　线性回归适合处理的是数值型数据。但也可以处理标签型数据，此时，须要先对标签数据做连续化预处理。

　　例如，性别，有两个可能的取值：男、女。为了将性别作为特征送给线性回归使用，可以设男=0，女=1.又如，苹果大小，这个特征，本来有三个标签取值：大、中和小。我们可以令小=1、中=2、大=3，然后再作为特征以便回归使用。

　　值得注意的是，不是所有标签型数据的特征都可以按照上述方法连续化。考察前面两个例子，其特征的取值是有偏序关系的，因而可以直接按照序关系取数值做连续化。然而，一个没有序关系的特征，就不能直接按照上述方法处理。举个例子，颜色，可能取得的值为：红、绿和蓝。那么，我们就不好直接令红=1，绿=2，蓝=3.因为它们之间没有既定的顺序，如果我们直接赋值 $1$、$2$、$3$，就会人为引入一个顺序关系，从而可能会带来问题。此时，可以采用的解决办法是，采用一个三维向量来表示三个特征的取值。设 $x$、$y$、$z$ 分别表示是否为红、绿、蓝。若是，则为 1，否则为 0.，那么，红、绿、蓝三种颜色可以分别表示为 $[1,0,0]$、$[0,1,0]$ 和 $[0,0,1]$。这样做的好处是，避免人为引入一个顺序关系。

3. 实战操作

　　前面介绍了线性回归的基本概念和理论。接下来，介绍一下在实际应用时，如何对数据做线性回归分析。实际上，有很多现成的软件包能够提供了线性回归功能。我们分别做一些介绍。

WEKA

　　打开软件，点击启动界面右侧的 Explorer 大按钮，打开数据处理窗口。

　　第 1 步，打开待处理数据集。点击 Open file...，在弹出的对话框中，选择数据集即可。这里选择 cpu.afff 数据集。

图 3：打开数据集

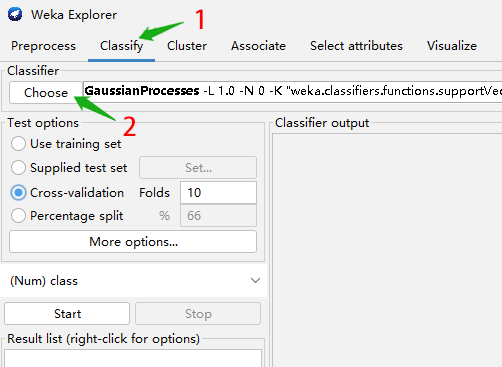
　　第 2 步，准备选择建模算法。（1）点击 Classify；（2）点击 Choose 按钮，选择算法。如图 2 所示。注意，软件里面并没有 Regression 这一选项卡。分类和回归算法都在 Classify 这一选项卡中。

图 4：选择算法

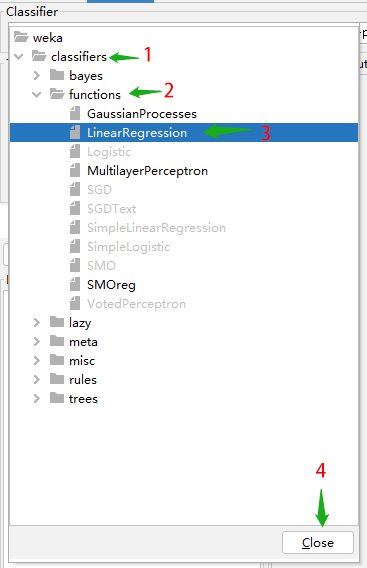
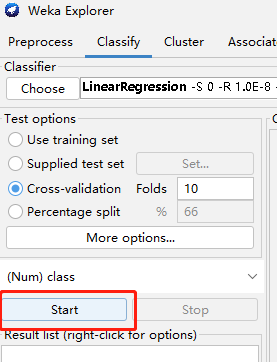
　　第 3 步，选择线性回归算法。在弹出的算法选择窗口里中，依次点击选择：classifiers->functions->LinearRegression。最后点击右下方 Choose 按钮确认。流程如图 3 所示。

图 5：选择线性回归算法

　　第 4 步，执行操作。点击 Start 按钮即可。

图 6：执行操作

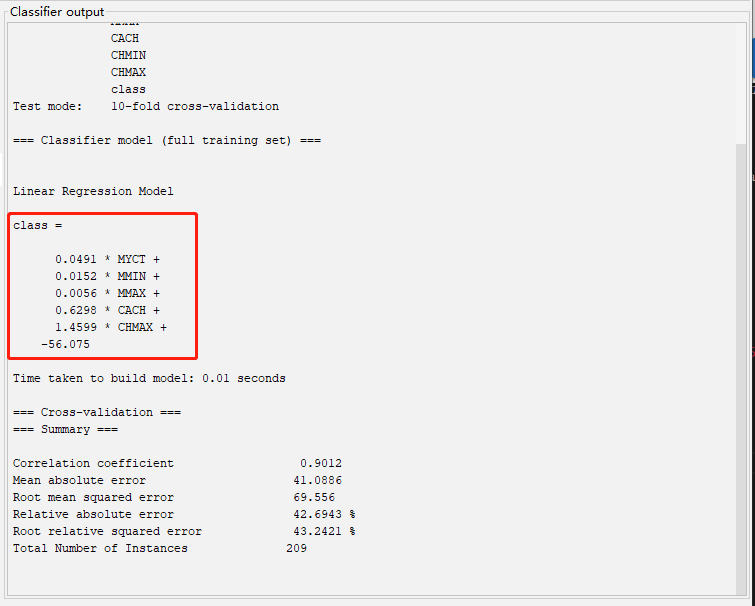
　　软件立即用线性回归方法进行建模。稍后，右侧会显示分析结果。线性回归方程为：$class=0.0491 \times MYCT+0.0152 \times MMIN+0.0056 \times MMAX+0.6298 \times CACH+1.4599 \times CHMAX-56.075$.如图 6 所示，图中红框标注出的就是回归直线方程。

图 7：分析结果