贡献者: jiangnan
1. 背景介绍
Ginzburg 谈到,最初他想要解决在超导体中出现的温差电现象。当超导体出现温度梯度时,导体中会出现特殊的超导电流,并且涌现出电磁场。当时的伦敦方程仅仅能解释其中的部分现象,而且伦敦方程预测普通金属与超导金属的界面能是负的,因此当时急需一个非电磁场起源的界面能来解决温差电现象。到 1950 年,Landau-Ginzburg 理论解决了这一问题。1
2. Landau-Ginzburg 理论
基于二级相变的理论,朗道提出在超导转变温度附近,超导体的自由能可以用一个复的序参量 $\psi = |\psi(r)|e^{i\phi(r)}$ 来描述,序参量的模平方 $|\psi(r)|^2$ 可以解释为超导电子密度,自由能密度可以写为2
\begin{equation}
f_s = f_n + \alpha(T) |\psi|^2 + \frac{\beta(T)}{2} |\psi|^4 + \frac{1}{2m^*} \left| \left(i\hbar \nabla - e^* A \right)\psi \right|^2 + \frac{H^2}{8\pi} ~.
\end{equation}
$f_s$ 代表体系进入超导态后的自由能,而 $f_n$ 代表体系处于正常金属态时的自由能。这里的 $A$ 是磁矢势。在超导温度附近,序参量 $\psi$ 出现由 0 到非 0 的转变,考虑一个最简单的情形,首先我们令 $H=A = 0$,即考虑一个无外加电磁场的体系,$f_n$ 看作一个常数,不妨设 $f_n=0$,并且 $\psi$ 在空间中是均匀的,即 $\nabla \psi = 0$. 此时的自由能可以写为
\begin{equation}
f_s = f_n + \alpha(T) |\psi|^2 + \frac{\beta(T)}{2} |\psi|^4 ~.
\end{equation}
对自由能关于序参量求偏导 $\partial f_s /\partial |\psi|^2 = 0$,可以得到自由能极点
\begin{align}
&|\psi_{\infty}|^2 = \frac{-\alpha}{\beta},|\psi_0|^2 = 0;\\
&f_s(|\psi_{\infty}|) = -\frac{\alpha^2}{\beta}, f_s(|\psi_0|) = 0 ~.
\end{align}
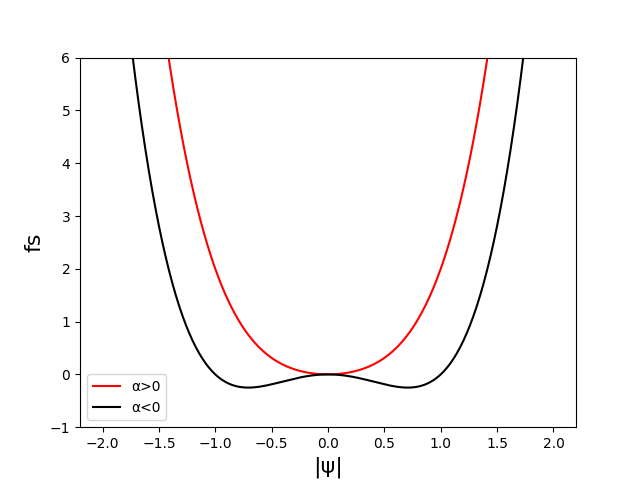
为保证稳定性,即 $|\psi|\rightarrow +\infty$ 时不会出现 $f_s \rightarrow -\infty$, 我们需要令 $\beta(T)$ 恒大于 0. 容易看到,当 $\alpha>0$ 时,$|\psi_\infty|^2 <0$ 这一极点不会出现,自由能随序参量增大而单调增加,因此在取到 $|\psi|=0$ 时自由能最低,无超导电子。而当 $\alpha<0$ 时,存在一个极小值点,$|\psi| = |\psi_{\infty}| = \sqrt{-\alpha/\beta}$,此时体系自由能为 $-\alpha^2/\beta$,即出现超导转变。Landau-Ginzburg 指出,在相变温度附近 $\alpha(T) = \alpha_0 (T - T_C)$,此处 $\alpha_0 > 0$,$T_c$ 为超导相变的临界温度。此时体系从临界温度之上变为临界温度之下即对应 $\alpha(T)$ 由正到负。Landau-Ginzburg 理论可以将各种实验客观测量用系数 $\alpha$、$\beta$ 表示出来,并预测各个物理量之间的关系。
图 1:相变图示,红色曲线代表 $\alpha>0$ 时的自由能随序参量的变化,此事随着序参量增加,自由能单调递增,因此自由能最低点取到序参量为 0,无超导电子。黑色曲线代表 $\alpha<0$ 时的情形,自由能极小值点出现在了一个非零的序参量处,系统处在超导态。原则上序参量的模长只能取正值,但我们在这里同时画了负值,便于理解。
3. 有效质量与有效电荷
Landau-Ginzburg 理论的提出在超导微观理论 BCS 理论之前,因此这套唯象理论的参数含义并不是个显而易见的事。根据各参数与实验的关系,有效质量不出现在可观测量中。这里的有效电荷的选取是一个有趣且深刻的问题。Ginzburg 一开始认为 $e^*$ 作为某些激发的有效电荷,应该跟电子电荷不同,甚至有可能依赖于材料的具体参数,比如压强、温度等等,然而 Landau 不觉得 $e^*$ 应该与电子电荷 $e$ 有任何的不同。因为电子电荷出现在诸如 Landau 参数 $\kappa$(这一参数会出现在界面能 $\sigma_{ns}$ 中),透射深度 $\delta_0$ 以及临界磁场 $H_c$ 中,而这些物理量在实验上可观测,所以 Ginzburg 通过对比实验数据得出结论,$e^* = (2-3)e$。到了 1957 年,Bardeen-Cooper-Schrieffer(BCS)理论出现后,大家意识到在超导中应该由 cooper 对来扮演传导电荷的角色,因此应该有 $e^* = 2e$, $m^* = 2m_e$。1959 年 Gor'kov 从 BCS 理论推导出 Landau-Ginzburg 方程后严格证明了这件事。
4. 临界磁场
在超导态中,当外界施加一个磁场,磁场强度高到一定程度时,会破坏超导相,使超导成为普通金属态。因此当考虑一个外磁场时,我们就需要考察超导态与普通金属态的自由能竞争。在计算超导态自由能时,不仅仅要考虑式 1 给出的能量,还要考虑超导态的抗磁能贡献。所以对于一个均匀超导体而言,当外加磁场大小为 $B_0$ 时(其内部完全抗磁,则有 $A=B=0$),
\begin{equation}
\Delta F = f_s -M H_0 -f_n - \frac{H_0^2}{8\pi}~.
\end{equation}
其中 $M = (H-H_0)/4\pi = -H_0/4\pi$。展开后得到
\begin{equation}
\Delta F = -\frac{\alpha^2}{2\beta} + \frac{H_0^2}{8\pi}~.
\end{equation}
可以看到,当 $H_0^2/8\pi > \alpha^2/\beta$ 时,体系倾向于普通金属态,而 $H_0^2/8\pi<\alpha^2/\beta$ 时,体系倾向于形成超导态。因此临界磁场 $H_C$ 的大小满足 $H_C^2/8\pi = \alpha^2/2\beta$。
5. 临界电流
根据连续性方程,$e^*\partial_t n = e^*\nabla \cdot J$, 给出电流的表达式为
\begin{equation}
J = \frac{e^*\hbar}{2im^*}(\psi \nabla \psi^* - \psi^* \nabla \psi) + \frac{e^{*2}\hbar}{m^*} A \psi^* \psi~.
\end{equation}
用序参量的相位与密度,写为
\begin{equation}
J = \frac{e^*}{m^*} |\psi|^2 (\hbar \nabla \phi - \frac{e^*}{c}A) ~,
\end{equation}
现在我们考虑粒子数密度是空间均匀的,仅有相位的梯度与磁矢势共同造成电流的存在,我们写为
\begin{equation}
J = e^* |\psi|^2 v_s~,
\end{equation}
其中 $v_s$ 代表准粒子的运动速度。将这一表达式代入到自由能中,我们得到自由的表达式变为
\begin{equation}
f_s = f_n + \alpha |\psi|^2 + \frac{\beta}{2}|\psi|^4 + |\psi|^2 \frac{m^*}{2} v_s^2 + \frac{H^2}{8\pi}~.
\end{equation}
此时处于热力学平衡态时,令自由能取极小值,得到超导电子数密度为
\begin{equation}
|\psi|^2 = \frac{-(\alpha + m^* v_s^2/2)}{\beta}~.
\end{equation}
主义,这里仅在 $\alpha+m^* v_s^2/2 <0$ 时体系才处于超导态,因此当准粒子的运动速度太高时,就会破坏超导态。同时,准粒子的运动速度越大,超导粒子的粒子数密度就越小。电流是粒子数密度与运动速度的乘积,即
\begin{equation}
J_s = e^* |\psi_{\infty}|^2 (1-\frac{m^* v_s^2}{2|\alpha|})v_s ~,
\end{equation}
对电流大小关于准粒子运动速度 $v_s$ 求导,$\partial J_s /\partial v_s = 0$,得到
\begin{equation}
1-\frac{3 m^* v_s^2}{2 |\alpha|} =0 ~,
\end{equation}
解得此时有
\begin{equation}
|\psi|^2 = \frac{2}{3}|\psi_{\infty}|^2, J^{max} = \frac{2e^* |\psi_{\infty}|^2}{3} \sqrt{\frac{2|\alpha|}{3m^*}} = \frac{2}{3}\sqrt{\frac{2}{3}}\frac{c H_c}{4\pi \lambda}~.
\end{equation}
这一表达式可以与伦敦方程计算临界电流的值对比,我们能够发现,伦敦方程的计算结果为 $J= c H_c/4\pi \lambda$。这一差别是由于伦敦方程没有考虑到超导电子密度会随着准粒子的运动速度增加而减小。
6. 透射深度
Landau-Ginzburg 理论解释了超导电流的参数依赖问题,在 Landau-Ginzburg 之前的伦敦方程的理论中,仅仅需要假设存在一种超导电流,这一电流满足伦敦方程,在结合麦克斯韦方程组即可得到许多关于超导现象的唯象结果。在伦敦方程中,计算得到的透射深度据超导唯象解释——伦敦方程 子节 4 ,其中的透射深度包含参数 $n_s$,即超导电子密度,在 Landau-Ginzburg 理论中,根据 $n_s = |\psi|^2 = -\alpha/\beta$,得到透射深度为
\begin{aligned}
\lambda = \sqrt{\frac{m^* c^2 \beta}{4\pi (e^*)^2 |\alpha|}}~.
\end{aligned}
实际上我们也可以直接从 Landau-Ginzburg 出发推导出透射深度的大小,考虑一个均匀体系,序参量密度不依赖空间变化,超导电流密度写为式 8 , 根据麦克斯韦方程组,$ \boldsymbol{\nabla}\boldsymbol{\times} B = 4\pi J/c$,对电流密度求旋度,我们得到
\begin{equation}
\frac{4\pi}{c} \boldsymbol{\nabla}\boldsymbol{\times} J_s = \boldsymbol{\nabla}\boldsymbol{\times} \boldsymbol{\nabla}\boldsymbol{\times} B = -\frac{4\pi (e^*)^2}{m^* c^2}|\psi|^2 B ~.
\end{equation}
根据 $ \boldsymbol{\nabla}\boldsymbol{\times} \boldsymbol{\nabla}\boldsymbol{\times} B = \nabla (\nabla \cdot B) - \nabla^2 B$ 得到
\begin{equation}
\nabla^2 B - \frac{4\pi (e^*)^2}{m^* c^2}|\psi|^2 B =0 ~,
\end{equation}
这一方程的解是指数衰减,给出磁场在超导体内的透射深度表达式为
\begin{equation}
\lambda^2 = \frac{m^* c^2}{4\pi (e^*)^2 |\psi|^2}~.
\end{equation}
7. 界面能
在计算界面能之前我们需要引入一个概念,相干长度。对自由能关于 $\psi^*$ 变分,得到无电磁场时的 Landau 方程为
\begin{equation}
\frac{-\hbar^2}{2m^*}\nabla^2 \psi + \alpha(T)\psi + \beta(T)|\psi|^2 \psi = 0~,
\end{equation}
这一方程确定序参量能随空间的变化。随着进入超导内部,序参量趋近于 $\psi_{\infty}$,对该方程进行归一化,进行变量替换 $f= \psi/\psi_{\infty}$,得到一个关于 $f$ 的方程为
\begin{equation}
-\frac{\hbar^2}{2m^* \alpha(T)} \nabla^2 f + f - |f|^2 f =0 ~,
\end{equation}
注意到 $\alpha(T)$ 是能量量纲,这里的 $\hbar^2/2m \alpha(T)$ 是长度平方量纲,因此定义相干长度为
\begin{equation}
\xi(T)^2 =\frac{\hbar^2}{2m^* |\alpha(T)|}~,
\end{equation}
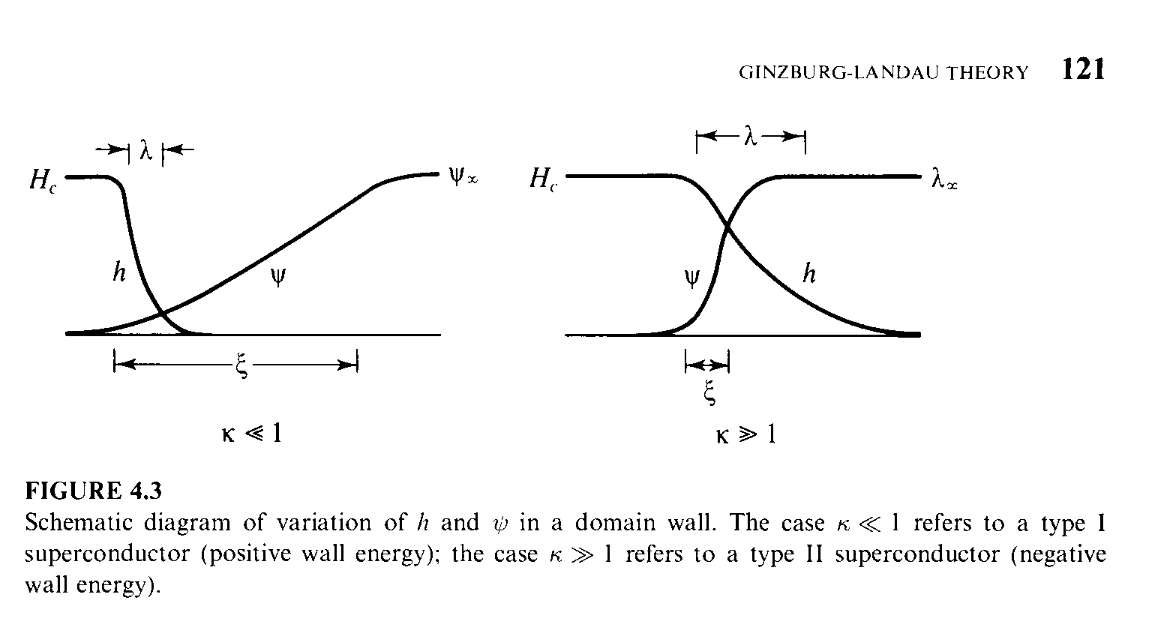
并进行变量代换 $x' = x/\xi(T)$,就完成了对朗道方程的参数无量纲化。因此 $\xi(T)$ 就是序参量随空间变化的特征长度。可以看到,在相变温度附近,相干长度发散,且随温度发散形式为 $(T_c-T)^{1/2}$。现在我们考虑简单的一维情形,通常我们在阅读文献时会遇到一个参数 $\kappa \equiv \lambda/\xi$,成为 Ginzburg-Landau 参数,用于区分 Type-I 超导体与 Type-II 超导体。注意到这里的 $\lambda$ 是透射系数,也即磁场进入超导体的深度,$\kappa$ 非常大时,意味着磁场可以很深地穿入超导体内部,而当 $\kappa$ 非常小时,磁场就大部分地被超导体排除出去
图 2 。当 $0<\kappa<1/\sqrt{2}$ 时,超导体就被分类为 Type-I 超导体,而当 $\kappa>1/\sqrt{2}$ 时,就被分类为 Type-II 超导体。这种分类与界面能的计算有关,Landau 与 Ginzburg 计算得到,当 $0<\kappa<1/\sqrt{2}$ 时,超导体与正常金属态之间的界面能为正,而当 $\kappa>1/\sqrt{2}$ 时,超导体与正常金属态之间的界面能为负。
图 2:超导态与正常金属态界面示意图,图源自 Micheal Tinkham 的《Introduction to superconductivitt》。
界面能的具体计算想法如下,在正常金属态内部添加磁场 $H=H_C$,因为当磁场大小达到临界磁场时,在超导体内部,超导态自由能加上抗磁能的大小与正常金属态自由能加上磁场能量大小相同,也就是说,此时正常金属态内部与超导体内部的自由等相同。此时计算体系整个的自由能再减去当体系全都是正常金属态的自由能,
\begin{equation}
\sigma_{ns} = \int \left( F_{sH}(x) - \frac{H(x)H_c}{4\pi} + \frac{H_c^2}{4\pi} -F_{n0} - \frac{H_c^2}{8\pi}\right)dx~.
\end{equation}
于是可以看到,这一自由能贡献对于超导态内部与正常金属态内部而言都是 0,只有在边界处有贡献。下面我们考虑两个极端情形的例子。
例 1 $\lambda =0$ 时的情形
当 $\lambda=0$ 时,$\xi$ 为有限值,此时对应 $\kappa \rightarrow 0$ 的情形,磁场完全无法进入超导体内部。给定边界条件,$f(z=0)=0, f(z=+\infty) = 1$,对应无量纲的 Ginzburg-Landau 方程的解为 $f=\tanh x' = \tanh x/\xi$。这一解的形式是常见的非线性方程的解,将这一序参量的解代入到式 21 中,计算得到界面能为 $-\alpha \hbar^2/2m \beta\xi$。注意到 $\alpha<0,\beta>0$,因此界面能为正。
例 2 $\xi = 0$ 时的情形
当 $\xi = 0$ 时,我们可以认为在界面处序参量没有平缓的变化,对于 $x>0,\psi(x) = \psi_{\infty}$,对于 $x<0,\psi(x)=0$。根据式 16 (这里有一点不同单位制之间的混用,但可以看到 $H$ 也是指数衰减,且衰减的特征长度也是 $\lambda$),可以得到当 $x>0$ 时,磁场强度的解为 $H(x) = H_c e^{-x/\lambda}$。同样将这一解带入到式 21 中,计算得到界面能为 $-3H_c^2 \lambda/16\pi$,此时界面能为负。
在最初 Landau 时代的超导实验室中,大部分的超导体都满足 $\kappa <<1$,因此 Landau 最初认为界面能为负并不值得仔细研究,后来合金超导体被发现了,它们的性质与纯超导体有很大的不同,正如后来 Landau 指出的,这些类型超导体恰是界面能为负的超导体,也即 Type-II 超导体,而之后发现的大部分超导体都是 Type-II。
1. ^ Ginzburg, Vitaly L. "Nobel Lecture: On superconductivity and superfluidity (what I have and have not managed to do) as well as on the “physical minimum” at the beginning of the XXI century." Reviews of Modern Physics 76.3 (2004): 981.
2. ^ wikipedia: Ginzburg-Landau theory