兰姆位移

贡献者： addis

本文处于草稿阶段。
本文缺少预备知识，初学者可能会遇到困难。

预备知识　玻尔原子模型

　　¹根据狄拉克的量子理论，氢原子的 $2S_{1/2}$ 和 $2P_{1/2}$ 能级应该具有相同的能量，但兰姆的实验发现它们有微弱的偏差，前者高出约

\begin{equation} \Delta E = 4.372 \times 10^{-6} \,\mathrm{eV} ~, \end{equation}

这被称为兰姆位移（Lamb shift）。

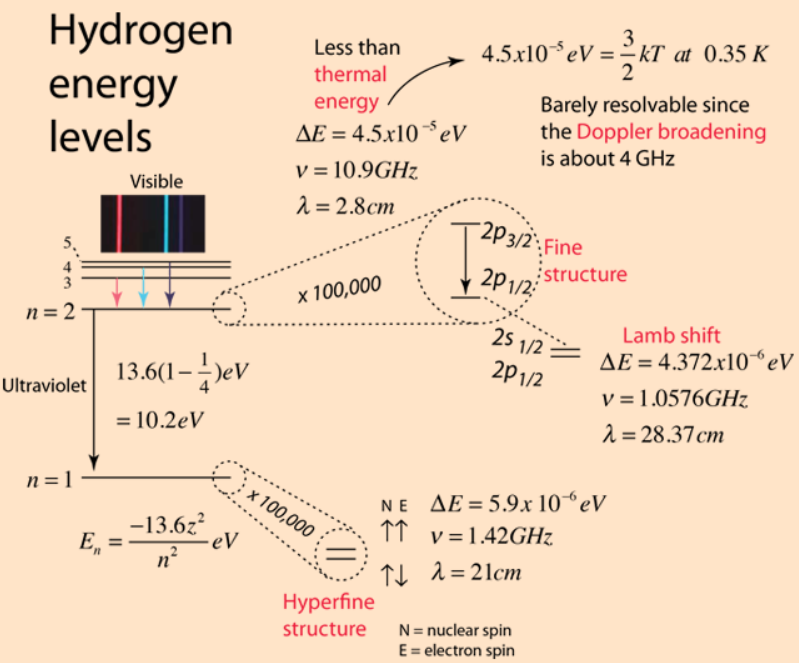
　　图 1 中显示，$n=2$ 能级的精细结构由 $2P_{3/2}$ 和 $2P_{1/2}$ 构成，而兰姆位移由 $2S_{1/2}$ 和 $2P_{1/2}$ 构成。兰姆位移和氢原子基态的超精细结构在同一个数量级。

图 1：氢原子的精细结构，超精细结构，以及兰姆位移（来自 HyperPhysics）

1. 补充

　　（未完成）Hans Bethe 首先用量子电动力学解释了兰姆位移。

　　（未完成）兰姆位移用于精确测量精细结构常数。

2. 能级修正

　　事实上，兰姆位移对每个能级都有微小的修正²

\begin{equation} \Delta E_{lamb} = \alpha^5 m_e c^2 \frac{k(n, 0)}{4n^3} \qquad (l = 0)~. \end{equation}

\begin{equation} \Delta E_{lamb} =\alpha^5 m_e c^2 \frac{1}{4n^3} \left[k(n,l) \pm \frac{1}{\pi(j+1/2)(l+1/2)} \right] \qquad (l \ne 0,\ j = l \pm 1/2)~. \end{equation}

其中 $k(n, 0)$ 约等于 $13$，$k(n, l) < 0.05$。将 $2S_{1/2}$（$l = 0$）和 $2P_{1/2}$（$n = 2,\ l = 1,\ s = 1/2$），得 $\Delta E = 4.365 \times 10^{-6} $。

1. ^ 参考 HyperPhysics 相关条目。
2. ^ 详见 Bethe, H.A.; Salpeter, E.E. (1957). Quantum Mechanics of One- and Two-Electron Atoms. Springer. p. 103.