量子隐形传态（综述）

                     

贡献者： 待更新

　　 （本文根据 CC-BY-SA 协议转载自原搜狗科学百科对英文维基百科的翻译）

图
图 1：量子隐形传态

　　 量子传输是一个传输量子信息(例如，原子或光子的确切状态)的过程，在这个过程中，借助于经典通信和先前发送和接收位置之间共享的量子纠缠，量子信息可以从一个位置传输到另一个位置。因为它依赖于经典通信，其速度不能超过光速，所以不能用于超光速传输或经典位通信。虽然已经证明可以在两个(纠缠的)量子之间传送一个或多个量子位的信息，但在比分子大的任何东西还没有实现这一点。[1]

　　 虽然这个名字的灵感来自小说中常用的传送，但量子传输仅限于信息的传送，而不是物质本身。量子传输不是一种传输方式，而是一种通信方式：它提供了一种将量子位从一个位置传输到另一个位置的方式，而不需要移动物理粒子。

　　 这个术语是物理学家查尔斯·贝内特创造的。1993 年，C. H. Bennett、G. Brassard、C. Crépeau、R. Jozsa、A. Peres 和 W. K. Wootters 发表了第一篇阐述了量子传输概念的开创性论文[2]。量子传输最初是在单个光子中实现的，[3] 后来在原子、离子、电子和超导电路等各种材料系统中得到证明。最新报道的量子传输距离是 1,400 km (870 mi)，由潘建伟小组利用 Micius 卫星进行空间量子传输。[4][5][6]

1. 非技术总结

　　 在与量子或经典信息理论相关的问题中，使用最简单的可能的信息单位——双态系统是很方便的。在经典信息中，这是一个比特，通常用 1 或 0(或真或假)来表示。比特的量子模拟是一个量子比特，或量子比特。量子比特编码一种称为量子信息的信息，它与 “经典” 信息截然不同。例如，量子信息既不能被复制(不克隆定理)，也不能被销毁(不删除定理)。

　　 量子传输提供了一种将一个量子比特从一个位置移动到另一个位置的机制，而不需要物理传输该量子比特通常所附着的底层粒子。就像电报的发明允许经典比特在大陆间高速传输一样，量子传输有朝一日也能以同样的方式移动量子比特。[7][8] 截至 2015 年，单光子、光子模式、单原子、原子系综、固体缺陷中心、单电子和超导电路的量子态已经被用作信息载体。[9]

　　 量子比特的移动不像互联网上的通信那样需要 “事物” 的移动：它不需要传输任何量子对象，但是每传送一个从发送者到接收者的量子比特，就需要传输两个经典比特。实际的传送协议要求创建纠缠量子态或贝尔态，并且它的两个部分在两个位置(源和目的地，或爱丽丝与鲍伯)之间共享。本质上，在移动一个量子比特之前，必须首先在两个位置之间建立某种量子通道。传送也需要建立一个经典的信息通道，因为每个量子比特必须传输两个经典比特。其原因是测量结果必须进行通信，并且必须通过普通的经典通信信道进行。起初，对这种经典渠道的需求似乎令人失望；然而，这与普通通信没有什么不同，普通通信需要电线、无线电或激光。更重要的是，贝尔态最容易被激光光子共享。因此，原则上，远程传输可以通过开放空间来完成，即不需要通过电缆或光纤发送光。

　　 单个原子的量子态已经被传送了。[10][10][10] 一个原子由几个部分组成：电子态的量子比特或原子核周围的电子层、原子核本身的量子比特、最后是组成原子的电子、质子和中子。物理学家已经传输了以原子电子状态编码的量子比特；他们没有传送核状态，也没有传送核本身。因此说 “一个原子被传送了” 是不准确的，应该说原子的量子态被传送了。因此，进行这种传输需要在接收位置有一批原子，可以让量子比特印在上面。传送核状态的重要性还不清楚：核状态确实会影响原子，例如在超精细分裂中，但是在一些未来的 “实际” 应用中，这种状态是否需要传输是有争议的。

　　 量子信息理论的一个重要方面是纠缠，它在不同的物理系统之间施加统计相关性。这些相关性即使在选择和独立执行测量时也是成立的，这是由于彼此之间的因果联系，正如贝尔试验实验所证实的那样。因此，在时空的一个点上进行的测量选择所产生的观测似乎会瞬间影响到另一个区域的结果，即使光还没有时间传播这个距离；这一结论似乎与狭义相对论不符(EPR 悖论)。然而，这种相关性永远不能被用来于以比光速更快的速度传输任何信息，这是一个包含在非通信定理中的陈述。因此，作为一个整体，量子传输永远不会超光速，因为量子比特在伴随的经典信息到来之前是无法重建的。

　　 理解量子传输需要在有限维线性代数、希尔伯特空间和投影矩阵中有良好的基础。利用二维复数值向量空间(希尔伯特空间)来描述量子比特，这是下面给出的形式化操作的主要基础。理解量子传输的数学并不绝对需要量子力学的工作知识，尽管没有这样的了解，方程的深层含义可能仍然相当神秘。

2. 协议

图
图 2：光子量子传输

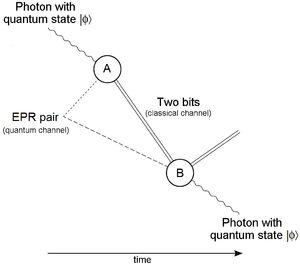
　　 量子传输的先决条件是要被传输的量子比特，能够传输两个经典比特(即四个状态之一)的常规通信信道，以及产生纠缠的 EPR 对量子比特的手段，将每个量子比特传输到两个不同的位置 A 和 B，对其中一个 EPR 对量子比特执行贝尔测量，并操纵另一对量子比特的量子状态。协议如下:

  1. 产生一个 EPR 对，一个量子比特发送到位置 A，另一个发送到位置 B。
  2. 在位置 A，EPR 对量子比特和要传送的量子比特(量子态 $\displaystyle |\phi \rangle $ $\displaystyle |\phi \rangle$ )执行贝尔测量，产生四个测量结果之一，这些结果可以用两个经典信息比特编码。然后，位置 A 的两个量子比特都被丢弃。
  3. 使用经典信道，两个比特从 A 发送到 B(考虑到光速，这是步骤 1 之后唯一可能耗时的步骤。)
  4. 由于在位置 A 进行的测量，位置 B 的 EPR 对量子比特处于四种可能状态之一。在这四种可能的状态中，有一种与原始量子状态相同 $\left| \phi \right\rangle$，和其他三个密切相关。这四种可能性中的其中一种实际上是用两个经典比特编码的。知道了这一点，位置 B 处的 EPR 对量子比特以三种方式之一修改，或者根本不修改，以产生与 $\left| \phi \right\rangle$ 相同的量子比特，即被选择传输的量子比特。

　　 值得注意的是，上面的协议假设量子位是可单独寻址的，这意味着量子比特是可区分的，并且是物理标记的。然而，也有两个相同的量子比特由于波函数的空间重叠而无法区分的情况。在这种情况下，量子比特不能单独控制或测量。然而，类似于上述的传输协议仍然可以(有条件地)通过利用两个独立准备的量子比特来实现，而不需要初始的 EPR 对。这可以通过在由两个无法区分的量子比特的波函数共享的分离区域 A 和 B 中进行空间局部化测量来解决量子比特的内部自由度(例如自旋或极化)来实现。[10]

3. 实验结果和记录

　　 1998 年的工作证实了最初的预测，[11] 在 2004 年 8 月，使用光纤传送的距离增加到 600 米。[12] 随后，量子传输的记录距离逐渐增加到 16 公里（9.9 英里），[13] 然后到 97 公里（60 英里）,[14] 现在是 143 公里（89 英里），这是在加那利群岛的两个岛上进行的露天实验中测量的。[15] 最近(截至 2015 年 9 月)有一项使用超导纳米线探测器的记录集，其在光纤上的距离达到了 102 公里（63 英里）。[16] 对于材料系统，记录距离为 21 米（69 英尺）。[17]

　　 2004 年，使用五光子纠缠演示了一种称为 “开放目的地” 传输的变体，接收器位于多个位置。[18] 还实现了两个单光子复合态的传输。[19] 2011 年 4 月，实验人员报告说，他们已经证明了光的波包在 10MHz 带宽内的传输，同时保留了强非经典叠加态。[20][21] 2013 年 8 月，报道了使用混合技术实现 “完全确定性” 量子传输的成果。[22] 2014 年 5 月 29 日，科学家宣布了一种通过量子传输传输数据的可靠方法。数据的量子传输以前是用非常不可靠的方法完成的。[23][24] 2015 年 2 月 26 日，中国科技大学合肥分校的科学家们在赵阳路和潘建伟的带领下，进行了第一次量子粒子多自由度传输实验。他们设法利用纠缠光子在 150 米（490 英尺）的距离内将量子信息从铷原子团传送到另一个铷原子团。[25][26][27] 2016 年，研究人员在合肥光纤网络上演示了两个独立源的量子传输，两个独立源相距 6.5 公里（4.0 英里）。[28] 2016 年 9 月，卡尔加里大学的研究人员在距离 6.2 公里（3.9 英里）的卡尔加里都市光纤网络上演示了量子传输。[29]

　　 研究人员还成功地利用量子传输在气体原子云之间传输信息，值得注意的是，气体云是宏观的原子集合。[30][31]

　　 2018 年，耶鲁大学的物理学家演示了逻辑编码量子比特之间确定性的传输 CNOT 操作。[32]

4. 正式陈述

　　 有多种方法可以用数学方法编写传输协议。有些协议的编写方式非常简洁但却比较抽象，有些冗长但直截了当且具体。下面展示的是后一种形式：冗长，但是具有简单且直接显示每个量子状态的优点。后面几节回顾更紧凑的符号。

　　 传输协议从量子态或量子比特开始 $\psi$ 在爱丽丝手中，她想传达给鲍勃。这个量子比特一般可以写为：

　　 $|\psi\rangle_c = \alpha|0\rangle_c + \beta|1\rangle_c$.

　　 以上的下标 $c$ 仅用于区分这种状态和下面公式中的 $A$ 和 $B$。

　　 接下来，该协议要求爱丽丝与鲍勃共享一个最大纠缠态。这种状态是通过爱丽丝与鲍勃之间的相互协议预先确定的，可以是公式所示的四种贝尔状态中的任何一种。具体是哪一个不重要。

　　 $|\Phi^+\rangle_{AB} = \frac{1}{\sqrt{2}} (|0\rangle_A \otimes |0\rangle_B + |1\rangle_A \otimes |1\rangle_B)$,

　　 $|\Phi^-\rangle_{AB} = \frac{1}{\sqrt{2}} (|0\rangle_A \otimes |0\rangle_B - |1\rangle_A \otimes |1\rangle_B)$,

　　 $|\Psi^+\rangle_{AB} = \frac{1}{\sqrt{2}} (|0\rangle_A \otimes |1\rangle_B + |1\rangle_A \otimes |0\rangle_B)$,

　　 $|\Psi^-\rangle_{AB} = \frac{1}{\sqrt{2}} (|0\rangle_A \otimes |1\rangle_B - |1\rangle_A \otimes |0\rangle_B)$.

　　 在下文中，假设爱丽丝与鲍伯共享状态 $\lvert \Phi^{+} \rangle_{AB}$。爱丽丝得到一对粒子中的一个，另一个给鲍勃。（这是通过将粒子准备在一起，然后从一个共同的来源分配给爱丽丝与鲍伯来实现的。）下标 $A$ 和 $B$ 是指处于纠缠态的爱丽丝粒子或鲍勃粒子。

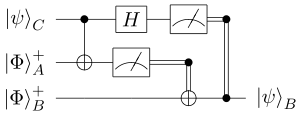
　　 此时，爱丽丝有两个粒子 ($C$，她想传送的那个；$A$，纠缠对中的一个)，鲍勃有一个粒子，$B$。在整个系统中，这三个粒子的状态为 $\lvert \psi \rangle_{C} \otimes \lvert \Phi^{+} \rangle_{AB} = (\alpha \lvert 0 \rangle_{C} + \beta \lvert 1 \rangle_{C}) \otimes \frac{1}{\sqrt{2}} (\lvert 0 \rangle_{A} \otimes \lvert 0 \rangle_{B} + \lvert 1 \rangle_{A} \otimes \lvert 1 \rangle_{B}).$

　　 爱丽丝将在贝尔基组（即四个贝尔态）上对她所拥有的两个粒子进行局部测量。为了使她的测量结果清晰，最好把爱丽丝的两个量子比特的状态写成贝尔基的叠加。这是通过使用以下易于验证的常规标识来完成的：

　　 $\lvert 0 \rangle \otimes \lvert 0 \rangle = \frac{1}{\sqrt{2}} (\lvert \Phi^{+} \rangle + \lvert \Phi^{-} \rangle),$

　　 $\lvert 0 \rangle \otimes \lvert 1 \rangle = \frac{1}{\sqrt{2}} (\lvert \Psi^{+} \rangle + \lvert \Psi^{-} \rangle),$

　　 $\lvert 1 \rangle \otimes \lvert 0 \rangle = \frac{1}{\sqrt{2}} (\lvert \Phi^{+} \rangle - \lvert \Phi^{-} \rangle),$

　　 $\lvert 1 \rangle \otimes \lvert 1 \rangle = \frac{1}{\sqrt{2}} (\lvert \Psi^{+} \rangle - \lvert \Psi^{-} \rangle).$

　　 和

　　 $|1\rangle \otimes |1\rangle = \frac{1}{\sqrt{2}} (| \Phi^{+} \rangle - |\Phi^{-}\rangle).$

　　 其中一个应用带有 $A$ 和 $C$ 下标的标识。总共三个颗粒态，其中 $A$)、$B$ 和 $C$ 三种颗粒态合起来，就变成以下四项叠加：

　　 $|\psi\rangle_{C} \otimes |\Phi^{+}\rangle_{AB} =\frac{1}{2} \left( |\Phi^{+}\rangle_{AC} \otimes (\alpha |0\rangle_{B} + \beta |1\rangle_{B}) + |\Phi^{-}\rangle_{AC} \otimes (\alpha |0\rangle_{B} - \beta |1\rangle_{B}) + |\Psi^{+}\rangle_{AC} \otimes (\beta |0\rangle_{B} + \alpha |1\rangle_{B}) +|\Psi^{-}\rangle_{AC} \otimes (\beta |0\rangle_{B} - \alpha |1\rangle_{B}) \right)$.

　　 以上只是基于爱丽丝的系统的基础改变量。没有执行任何操作，三个粒子仍处于相同的总状态。当爱丽丝在贝尔的基础上测量她的两个量子比特 $A$、$C$ 时，实际的传输发生了

　　 $ |\Phi^{+}\rangle_{AC}, |\Phi^{-}\rangle_{AC}, |\Psi^{+}\rangle_{AC}, |\Psi^{-}\rangle_{AC}. $

　　 实际上，这种测量可以通过一系列指向两个粒子的激光脉冲来实现
footnote{来源请求}。鉴于上述表达式，显然爱丽丝（局部）测量的结果是，三粒子状态将坍缩为以下四种状态之一（获得每种状态的概率相等）：

　　 爱丽丝的两个粒子现在处于四种贝尔态中的一种相纠缠，而爱丽丝和鲍勃的粒子之间原本共享的纠缠现在被打破了。鲍勃的粒子呈现上述四种叠加态之一。注意鲍勃的量子比特现在处于一种类似于被传输的状态。鲍勃的量子比特的四种可能状态是等待传输的单一图像。

　　 爱丽丝的贝尔测量结果告诉她系统处于上述四种状态中的哪一种。她现在可以通过一个经典频道把结果发送给鲍勃。两个经典比特可以传达她获得的四个结果中的任意一个。

　　 鲍勃收到爱丽丝的信息后，他将知道他的粒子处于上述四种状态中的哪一种。利用这些信息，他对他的粒子执行一个适当的单位运算，以将其转换为期望的状态 $\alpha|0\rangle_B + \beta|1\rangle_B$:

　　 $\sigma_3 = \begin{pmatrix}1 & 0 \\0 & -1\end{pmatrix}$

　　 来恢复状态。

　　 这样就实现了传输。上述三个量子门对应于π角度(180°)围绕坐标轴(X, Y 和 Z)的旋转。

图
图 3：用 Q-Kit 演示单个量子比特的量子传输

　　 一些备注:

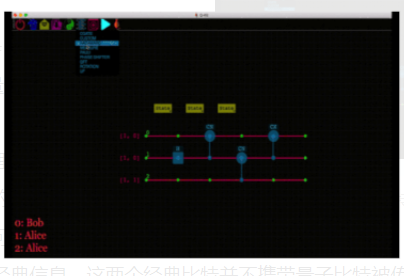
　　 利用量子电路模拟器 Q-Kit，用图形界面演示了单量子比特量子隐形传输的量子电路。爱丽丝在量子比特 2 中的状态通过爱丽丝与鲍伯、量子比特 1 和 0 之间的一对先前纠缠的量子比特被转移到鲍勃的量子比特 0。

5. 替代符号

　　 有各种不同的符号用于描述传输协议。一个常见的方法是使用量子门的符号。在上面的推导中，可以用量子门写出基的幺正变换(从标准乘积基到贝尔基)。直接计算表明，该量子门由下式给出

　　 $G=(H\otimes I)C_N$

　　 其中，$H$ 是沃尔什-哈达玛门的一个量子比特；$C_N$ 是受控反闸。

图
图 4：量子隐形传态的图解形式。[1] 采用彭罗斯图形符号。[2] 在形式上，这种计算是在匕首紧凑类别中进行的。这导致了量子隐形传态在分类量子力学中的抽象描述。
图
图 5：量子传输的量子电路示意

6. 纠缠交换

　　 量子传输不仅可以应用于纯态，也可以应用于混合态，这种混合态可以被视为纠缠对的单个子系统的状态。所谓的纠缠交换是一个简单的且具有说明性的例子。

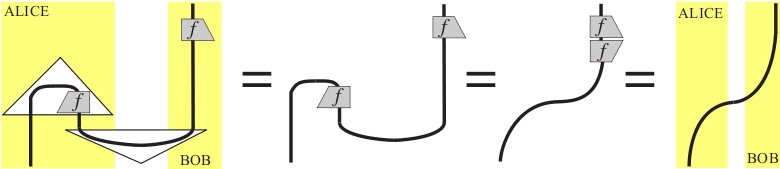
　　 如果爱丽丝有一个粒子与鲍勃拥有的粒子纠缠在一起，鲍勃将它传送给卡罗尔，然后，爱丽丝的粒子与卡罗尔的粒子纠缠在一起。

　　 描述这种情况的更对称的方式如下：爱丽丝有一个粒子，鲍勃有两个，卡罗尔有一个。爱丽丝的粒子和鲍勃的第一粒子纠缠在一起，鲍勃的第二粒子和卡罗尔的粒子纠缠在一起：

　　 ___ / \ 爱丽丝-:-:-:-:-:-:-鲍勃 1 -:-鲍勃 2-:-:-:-:-:-:-:-卡罗尔 _ _ _ _ _ _/

　　 此时，如果鲍勃在贝尔态的基础上对他的两个粒子进行投影测量，并将结果传送给卡罗尔，根据上述传送方案，鲍勃的第一粒子的状态可以传送给卡罗尔。虽然爱丽丝和卡罗尔从来没有相互作用过，但他们的粒子现在已经纠缠在一起了。

　　 鲍勃·科克尔根据范畴量子力学给出了纠缠交换的详细图解推导。

7. 传输协议的推广

　　 上述量子比特的基本传输协议已经在几个方向上进行了推广，特别是关于传输的系统的维度和参与方(作为发送方、控制方或接收方)的数量。

　　 三维系统

　　 对三维系统的概括(所谓的量子比特)是直截了当的，班尼特等人在原始论文中已经讨论过。[35] 两个量子比特的最大纠缠态必须用两个量子比特的最大纠缠态来代替，而贝尔测量必须用最大纠缠标准正交基定义的测量来代替。沃纳在 2001 年讨论了所有可能的这种概括。[35] 无穷维连续变量系统的推广 [36]，导致了第一个无条件运作的量子传输实验。[37]

　　 多部分版本

　　 使用多部分纠缠态而不是双部分最大纠缠态，可以实现以下几个新功能：发送者可以传送信息给几个接收者，或者发送相同的状态给所有接收者(这样可以减少过程所需的纠缠量) [38] 或者传输多部分状态 [39] 或者以接收方需要合作来提取信息的方式发送单个状态。[40] 查看后一种设置的另一种方式是，某些参与方可以控制其他参与方是否可以传输。

8. 逻辑门传输

　　 一般来说，可以传输混合态ρ，并且在传输期间应用线性变换ω，从而允许对量子信息进行数据处理。这是量子信息处理的基础构件之一。如下所示。

8.1 概述

　　 一般的传输方案可以描述如下。传输方案涉及三个量子系统，系统 1 是爱丽丝传输的(未知)状态 $\rho$，系统 2 和 3 处于最大纠缠状态 $\omega$，分别分配给爱丽丝与鲍伯。整个系统就处于这种状态：

\begin{align} \rho \otimes \omega.~ \end{align}

　　 一个成功的隐形传态过程是 LOCC 量子信道 $\varphi$，它满足

\begin{align} \left(\mathrm{Tr}_{12} \otimes \Phi \right) (\rho \otimes \omega) = \rho,~ \end{align}
其中，$\mathrm{Tr}_{12}$ 是针对系统 1 和系统 2 的部分跟踪操作；$\circ$ 表示地图的组成。这描述了萨丁格绘景的频道。

　　 对于所有可观察到的 $O$ 论饱动体系，取海森堡绘景的伴随映射，其成功条件为：

\begin{align} \left\langle \Phi (\rho \otimes \omega) \left| I \otimes O \right| \Phi (\rho \otimes \omega) \right\rangle = \left\langle \\rho \left| O \right| \rho \right\rangle~ \end{align}
$I \otimes O$ 中的张量因子为 $1_2 \otimes 3$，而 $\rho \otimes \omega$ 中的张量因子为 $1 \otimes 2_3$。

8.2 更多详情

　　 可以更明确地描述建议的信道φ。为了开始传送，爱丽丝对她所拥有的两个子系统(1 和 2)进行局部测量。假设本地测量有影响

　　 $F_i = M_i^2.$

　　 如果测量记录了第 $i$ 个结果, 则整体状态将坍缩为 $(M_i \otimes I)(\rho \otimes \omega)(M_i \otimes I).$

　　 $(M_i \otimes I)$ 中的张量因子为 $12 \otimes 3$, 而 $\rho \otimes \omega$ 中的张量因子为 $1 \otimes 23$。然后饱和在系统 3 上应用相应的本地操作 $\psi_i$。在组合系统中，这由 $(\text{Id} \otimes \Psi_i)(M_i \otimes I)(\rho \otimes \omega)(M_i \otimes I).$

　　 其中，Id 是复合系统 $12$ 上的标识映射。

　　 因此，通过 $\phi$ 定义为 $\Phi(\rho \otimes \omega) = \sum_i (\text{Id} \otimes \Psi_i)(M_i \otimes I)(\rho \otimes \omega)(M_i \otimes I)$

　　 注意 $\phi$ 满足 LOCC 的定义。如上所述，如果在饱和的系统中，所有可观察到的 $O$ 都是相等的，那么就可以认为传输是成功的。

　　 $\langle \Phi(\rho \otimes \omega), I \otimes O \rangle = \langle \rho, O \rangle$

　　 等式的左边是:

\begin{equation} \sum_{i} \langle (\text{Id} \otimes \Psi_{i})(M_{i} \otimes I)(\rho \otimes \omega)(M_{i} \otimes I), I \otimes \Psi_{i}^{*}(O) \rangle = \sum_{i} \langle (M_{i} \otimes I)(\rho \otimes \omega)(M_{i} \otimes I), I \otimes \Psi_{i}^{*}(O) \rangle~ \end{equation}
式中，$\Psi_{i}^{*}$ 是海森堡绘景中 $\psi$ 的伴随。假设所有物体都是有限维的，则 $\sum_{i} \text{Tr} \left( (\rho \otimes \omega)(F_{i} \otimes \Psi_{i}^{*}(O)) \right).$

　　 传输的成功标准有以下表达式:

　　 $\sum_{i} \text{Tr} \left( (\rho \otimes \omega)(F_{i} \otimes \Psi_{i}^{*}(O)) \right) = \text{Tr} \\ \rho \cdot O.$

9. 对这一现象的局部解释

　　 针对量子力学的多世界解释，大卫·多伊奇和帕特里克·海登提出了量子传输的局部解释。他们的论文断言爱丽丝发送给鲍勃的两个比特包含 “局部不可访问的信息”，导致量子态的量子传输。“量子信息流经经典通道的能力...，幸存的退相干，是...量子传输的基础。”[41]

10. 参考文献

  1. Deutsch, David; Hayden, Patrick (2017-03-16). "How Quantum Teleportation Actually Works". Proceedings of the Royal Society of London, Series A. 456 (1999): 1759. arXiv:quant-ph/9906007. doi:10.1098/rspa.2000.0585..
  2. A. Zeilinger, Dance of the Photons, Farrar, Straus and Giroux, New York, 2010, p. 46. ("The quantum mechanical solution [to teleportation] was proposed in 1993 by an international collaboration of six theoretical physicists: Charles Bennett of IBM; Gilles Brassard, Claude Crépeau, and Richard Jozsa of the University of Montreal; Asher Peres of the Technion (the Israel Institute of Technology in Haifa), and William K. Wootters of Williams College... The Bennett-Brassard-Crépeau-Jozsa-Peres-Wootters paper has the title 'Teleporting an Unknown Quantum State via Dual Classical and Einstein-Podolsky-Rosen channels.' To have the word 'teleporting' in the title of a physics paper was quite unusual at the time, since teleportation was considered to be part of science fiction and a somewhat shaky topic. But apparently, there was no better name for the interesting theoretical discovery these scientists made, and it was a very fitting name indeed.").
  3. Bouwmeester, D.; et al. (1997). "Experimental quantum teleportation". Nature. 390 (6660): 575–579. arXiv:1901.11004. Bibcode:1997Natur.390..575B. doi:10.1038/37539..
  4. Ren, Ji-Gang; Xu, Ping; Yong, Hai-Lin; Zhang, Liang; Liao, Sheng-Kai; Yin, Juan; Liu, Wei-Yue; Cai, Wen-Qi; Yang, Meng (2017). "Ground-to-satellite quantum teleportation". Nature. 549 (7670): 70–73. arXiv:1707.00934. Bibcode:2017Natur.549...70R. doi:10.1038/nature23675. PMID 28825708..
  5. Kluger, Jeffrey. "A 'Teleportation' to Outer Space". Time. Retrieved 2017-07-16..
  6. "Scientists Teleport A Photon From Earth To Orbit For The First Time". Huffington Post (in 英语). 2017-07-12. Retrieved 2017-07-16..
  7. Kimble, H. J. (2008). "The quantum internet". Nature. 453 (7198): 1023–1030. arXiv:0806.4195. Bibcode:2008Natur.453.1023K. doi:10.1038/nature07127. PMID 18563153..
  8. Michael Lucy (2018-04-13). "The quantum internet is already being built". Cosmos (78). Retrieved 2018-10-08..
  9. S. Pirandola, J. Eisert, C. Weedbrook, A. Furusawa, and S. L. Braunstein (2015). "Advances in quantum teleportation". Nature Photonics. 9 (10): 641–652. arXiv:1505.07831. Bibcode:2015NaPho...9..641P. doi:10.1038/nphoton.2015.154.CS1 maint: Uses authors parameter (link).
  10. New York Times, Scientists Teleport Not Kirk, but an Atom (2004).
  11. D. Boschi; S. Branca; F. De Martini; L. Hardy; S. Popescu (1998). "Experimental Realization of Teleporting an Unknown Pure Quantum State via Dual Classical and Einstein-Podolsky-Rosen Channels". Physical Review Letters. 80 (6): 1121–1125. arXiv:quant-ph/9710013. Bibcode:1998PhRvL..80.1121B. doi:10.1103/PhysRevLett.80.1121..
  12. Rupert Ursin (August 2004). "Quantum teleportation across the Danube". Nature. 430. Retrieved 2010-05-22..
  13. Jin, Xian-Min; Ren, Ji-Gang; Yang, Bin; Yi, Zhen-Huan; Zhou, Fei; Xu, Xiao-Fan; Wang, Shao-Kai; Yang, Dong; Hu, Yuan-Feng; Jiang, Shuo; Yang, Tao; Yin, Hao; Chen, Kai; Peng, Cheng-Zhi; Pan, Jian-Wei (16 May 2010). "Experimental free-space quantum teleportation". Nature Photonics. 4 (6): 376. Bibcode:2010NaPho...4..376J. doi:10.1038/nphoton.2010.87..
  14. Ma, Xiao-Song; Herbst, Thomas; Scheidl, Thomas; Wang, Daqing; Kropatschek, Sebastian; Naylor, William; Wittmann, Bernhard; Mech, Alexandra; Kofler, Johannes; Anisimova, Elena; Makarov, Vadim; Jennewein, Thomas; Ursin, Rupert; Zeilinger, Anton (5 September 2012). "Quantum teleportation over 143 kilometres using active feed-forward". Nature. 489 (7415): 269–73. Bibcode:2012Natur.489..269M. doi:10.1038/nature11472. PMID 22951967..
  15. Ma, X. S.; Herbst, T.; Scheidl, T.; Wang, D.; Kropatschek, S.; Naylor, W.; Wittmann, B.; Mech, A.; et al. (2012). "Quantum teleportation over 143 kilometres using active feed-forward". Nature. 489 (7415): 269–273. Bibcode:2012Natur.489..269M. doi:10.1038/nature11472. PMID 22951967..
  16. Takesue, Hiroki; et al. (2015-10-20). "Quantum teleportation over 100 km of fiber using highly efficient superconducting nanowire single-photon detectors". Optica. 2 (10): 832–835. arXiv:1510.00476. doi:10.1364/OPTICA.2.000832. Retrieved 2016-07-26..
  17. Nölleke, Christian; Neuzner, Andreas; Reiserer, Andreas; Hahn, Carolin; Rempe, Gerhard; Ritter, Stephan (2013). "Efficient Teleportation between Remote Single-Atom Quantum Memories". Physical Review Letters. 110 (14): 140403. arXiv:1212.3127. Bibcode:2013PhRvL.110n0403N. doi:10.1103/PhysRevLett.110.140403. PMID 25166964..
  18. Nature 430, 54-58 (1 July 2004) http://www.nature.com/nature/journal/v430/n6995/full/nature02643.html.
  19. Experimental quantum teleportation of a two-qubit composite system Qiang Zhang, Alexander Goebel, Claudia Wagenknecht, Yu-Ao Chen, Bo Zhao, Tao Yang, Alois Mair, Jörg Schmiedmayer & Jian-Wei Pan Nature Physics 2, 678–682.
  20. Lee, Noriyuki; Hugo Benichi; Yuishi Takeno; Shuntaro Takeda; James Webb; Elanor Huntington; Akira Furusawa (April 2011). "Teleportation of Nonclassical Wave Packets of Light". Science. 332 (6027): 330–333. arXiv:1205.6253. Bibcode:2011Sci...332..330L. CiteSeerX 10.1.1.759.1059. doi:10.1126/science.1201034. PMID 21493853..
  21. Trute, Peter. "Quantum teleporter breakthrough". The University Of New South Wales. Retrieved 17 April 2011..
  22. Takeda et al., "Deterministic quantum teleportation of photonic quantum bits by a hybrid technique", Nature, August 2013..
  23. Markoff, John (29 May 2014). "Scientists Report Finding Reliable Way to Teleport Data". The New York Times. Retrieved 29 May 2014..
  24. Pfaff, W.; et al. (29 May 2014). "Unconditional quantum teleportation between distant solid-state quantum bits". Science. 345 (6196): 532–535. arXiv:1404.4369. Bibcode:2014Sci...345..532P. doi:10.1126/science.1253512. PMID 25082696..
  25. "Two quantum properties teleported together for first time". PhysicsWorld.com. 27 February 2015..
  26. Wang, Xi-Lin; Xin-Dong Cai; Zu-En Su; Ming-Cheng Chen; Dian Wu; Li Li; Nai-Le Liu; Chao-Yang Lu; Jian-Wei Pan (26 February 2015). "Quantum teleportation of multiple degrees of freedom of a single photon". Nature. 518 (7540): 516–519. Bibcode:2015Natur.518..516W. doi:10.1038/nature14246. PMID 25719668..
  27. Xia, Xiu-Xiu; Qi-Chao Sun; Qiang Zhang; Jian-Wei Pan (2018). "Long distance quantum teleportation". Quantum Science and Technology. 3 (1): 014012. Bibcode:2018QS&T....3a4012X. doi:10.1088/2058-9565/aa9baf..
  28. Sun, Qi-Chao; Mao, Ya-Li; Chen, Sijing; Zhang, Wei; Jiang, Yang-Fan; Zhang, Yanbao; Zhang, Weijun; Miki, Shigehito; Yamashita, Taro; Terai, Hirotaka; Jiang, Xiao; Chen, Teng-Yun; You, Lixing; Chen, Xianfeng; Wang, Zhen; Fan, Jingyun; Zhang, Qiang; Pan, Jian-Wei (2016-09-19). "Quantum teleportation with independent sources and prior entanglement distribution over a network". Nature Photonics (in 英语). 10 (10): 671–675. arXiv:1602.07081. doi:10.1038/nphoton.2016.179. ISSN 1749-4893..
  29. Valivarthi, Raju; Puigibert, Marcel.li Grimau; Zhou, Qiang; Aguilar, Gabriel H.; Verma, Varun B.; Marsili, Francesco; Shaw, Matthew D.; Nam, Sae Woo; Oblak, Daniel (2016-09-19). "Quantum teleportation across a metropolitan fibre network". Nature Photonics. 10 (10): 676–680. arXiv:1605.08814. Bibcode:2016NaPho..10..676V. doi:10.1038/nphoton.2016.180. ISSN 1749-4885..
  30. "Quantum teleportation between atomic systems over long distances". Phys.Org..
  31. Krauter, H.; Salart, D.; Muschik, C. A.; Petersen, J. M.; Shen, Heng; Fernholz, T.; Polzik, E. S. (2 June 2013). "Deterministic quantum teleportation between distant atomic objects". Nature Physics. 9 (7): 400. arXiv:1212.6746. Bibcode:2013NatPh...9..400K. doi:10.1038/nphys2631..
  32. K.S. Chou et al., Deterministic teleportation of a quantum gate between two logical qubits. https://arxiv.org/abs/1801.05283.
  33. Chuang, Nielsen. Quantum Computation and Quantum Information. pp. 26–27..
  34. Bob Coecke, "The logic of entanglement". Research Report PRG-RR-03-12, 2003. arXiv:quant-ph/0402014 (8 page shortversion) (full 160 page version).
  35. C. H. Bennett, G. Brassard, C. Crépeau, R. Jozsa, A. Peres, W. K. Wootters (1993). "Teleporting an Unknown Quantum State via Dual Classical and Einstein–Podolsky–Rosen Channels". Phys. Rev. Lett. 70 (13): 1895–1899. Bibcode:1993PhRvL..70.1895B. CiteSeerX 10.1.1.46.9405. doi:10.1103/PhysRevLett.70.1895. PMID 10053414.CS1 maint: Uses authors parameter (link).
  36. Braunstein, S. L.; Kimble, H. J. (1998). "Teleportation of Continuous Quantum Variables" (PDF). Phys. Rev. Lett. 80 (4): 869–872. Bibcode:1998PhRvL..80..869B. doi:10.1103/PhysRevLett.80.869..
  37. Furusawa, A.; Sørensen, J. L.; Braunstein, S. L.; Fuchs, C. A.; Kimble, H. J.; Polzik, E. S. (1998). "Unconditional Quantum Teleportation". Science. 282 (5389): 706–709. Bibcode:1998Sci...282..706F. doi:10.1126/science.282.5389.706..
  38. W. Dür and J. I. Cirac (2000). "Multiparty teleportation". J. Mod. Opt. 47 (2–3): 247–255. Bibcode:2000JMOp...47..247D. doi:10.1080/09500340008244039..
  39. Yeo, Ye; Chua, Wee Kang (2006). "Teleportation and Dense Coding with Genuine Multipartite Entanglement". Phys. Rev. Lett. 96 (6): 060502. arXiv:quant-ph/0510029. Bibcode:2006PhRvL..96f0502Y. doi:10.1103/PhysRevLett.96.060502. PMID 16605974..
  40. Karlsson, Anders; Bourennane, Mohamed (1998). "Quantum teleportation using three-particle entanglement". Phys. Rev. A. 58 (6): 4394–4400. Bibcode:1998PhRvA..58.4394K. doi:10.1103/PhysRevA.58.4394..
  41. Deutsch, David; Hayden, Patrick (1999). "Information Flow in Entangled Quantum Systems". Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences. 456 (1999): 1759–1774. arXiv:quant-ph/9906007. Bibcode:2000RSPSA.456.1759H. doi:10.1098/rspa.2000.0585..

                     

© 小时科技 保留一切权利