贡献者: 1917KMN; 蒋岱兵
1. 实验装置与实验现象
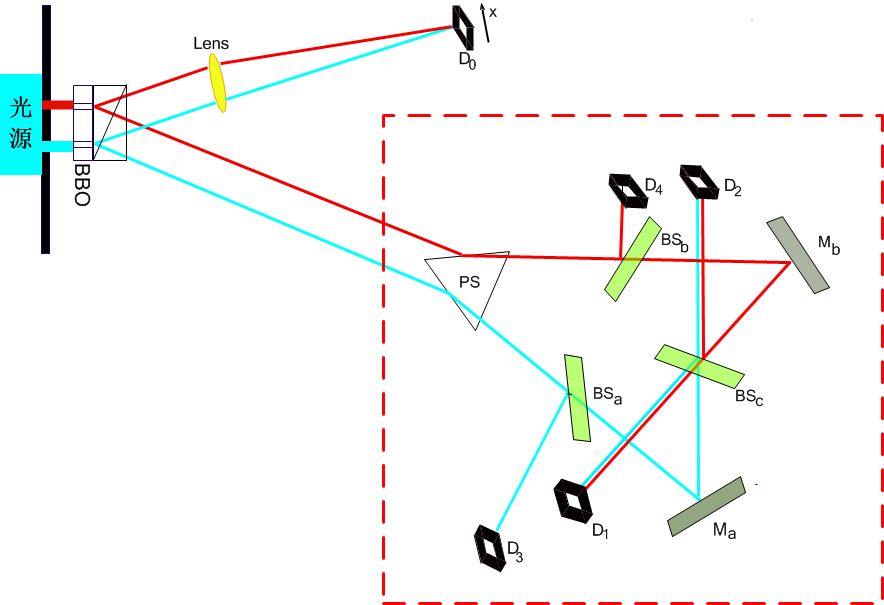
图 1:实验装置图(图片来自维基百科)
如图 1 所示,左上角的光源发射光子,光子随后经过双缝。把红色路径标识的缝记为左缝,另一条则称为右缝。光子经过双缝后会进入 $BBO$ 晶体。$BBO$ 将会吸收每一个入射的光子并发射出两个纠缠的光子。这两个光子经过棱镜后会分别射向不同的方向。我们把射向屏幕 $D_0$ 的光子称为 $A$ 光子,另一个称为 $B$ 光子。$D_0$、$D_1$、$D_2$、$D_3$、$D_4$ 都是感光屏。$BS_a$、$BS_b$、$BS_c$ 是半透半反射镜,入射的光子有一半概率反射、一半概率透射。$M_a$、$M_b$ 是全反射镜。在经过 $BS_c$ 后,从两条缝中射出的光子所产生的 $B$ 光子的路径完全重合。从双缝到 $D_1$、$D_2$、$D_3$、$D_4$ 光程远大于到 $D_0$ 的光程,因此可以在观察到 $D_0$ 上的现象后再对虚线框中的 $B$ 光子观测系统进行调整。
在进行实验时,按如下的步骤操作:
(i)令光源每次只发射一个光子。
(ii)观察 $D_0$ 屏幕上的光子落点,并记下另外四个屏幕中感光的屏幕编号。若 $D_i(i=1,2,3,4)$ 屏幕感光,则将对应的光子落点记为 $i$ 类点。重复进行多次。
(iii)只开放左狭缝,观察 $D_0$ 屏幕上的光子落点,这类落点记为 $L$ 类落点。重复进行多次。然后,在只开放右狭缝的情况下进行同样的工作,对应的落点记为 $R$ 类落点。
实验完成后,将光子的落点画在图上,构成光强分布图。将 $i(i=1,2,3,4,L,R)$ 类点的分布称为 $i$ 类分布,所有光子落点的分布称为总分布。实验现象如下:
(i)总分布图中不存在干涉条纹。
(ii)$1$ 类分布与 $2$ 类分布中存在干涉条纹。
(iii)$3$ 类分布与 $4$ 类分布中不存在干涉条纹。
(iv)$3$ 类分布等于 $R$ 类分布,$4$ 类分布等于 $L$ 类分布。
(v)总分布等于 $|\alpha|^2$ 倍的 $L$ 类分布与 $|\beta|^2$ 倍的 $R$ 类分布之和。
2. 假设与约定
为方便下面的讨论,这里做一些必要的简化,并对符号作出约定。
光子经过双缝后,其态矢量是确定的。显然,这个态矢可以写为如下的形式:
\begin{equation}
\left\lvert \Psi(t=0) \right\rangle =\alpha \left\lvert \chi_L(t=0) \right\rangle +\beta \left\lvert \chi_R(t=0) \right\rangle ~.
\end{equation}
其中 $ \left\lvert \chi_L(t=0) \right\rangle $ 表示这样的一个态:$t=0$ 时刻,光子刚通过狭缝,此时对光子的位置进行测量,可以完全肯定它来自于左边的狭缝。若 $t=0$ 时刻,从两边狭缝透射出的波函数没有任何重叠(即 $\chi_L(t=0)\chi_R(t=0)$ 处处为零),这样的效果就可以达成。$ \left\lvert \chi_R(t=0) \right\rangle $ 的定义同理。所以,在光子刚经过狭缝时,对光子的位置进行测量,就可以完全肯定光子经过了哪条狭缝,且经过左边狭缝的概率为 $|\alpha|^2$,经过右边狭缝的概率为 $|\beta|^2$。这两个概率的和为 $1$(这就保证了态矢量 $ \left\lvert \Psi \right\rangle $ 的归一化),而它们的具体值取决于光源的位置和两条狭缝的宽度等参数,这里不讨论。通过以上的定义,还可以看出 $ \left\lvert \psi_L(t=0) \right\rangle $ 正交于 $ \left\lvert \psi_R(t=0) \right\rangle $,$ \left\lvert \phi_L(t=0) \right\rangle $ 正交于 $ \left\lvert \phi_R(t=0) \right\rangle $,这是因为从两边狭缝透射出的波函数没有任何重叠。
接下来研究 $BBO$ 晶体对态矢量的作用。简单起见,假设光子经过双缝后立刻受到 $BBO$ 的作用。当一个光子射入 $BBO$ 晶体时,将产生一对除自旋外各种属性和状态都相同的光子,且这对光子的属性和状态与入射的光子也相同。设 $\mathscr{E}_A$ 为 $A$ 光子的轨道态空间(即不考虑自旋的态空间),$\mathscr{E}_B$ 为 $B$ 光子的轨道态空间,$\mathscr{E}_I$ 为入射光子的轨道态空间。经过 $BBO$ 晶体后整个体系的轨道态空间即为 $\mathscr{E}_A$ 和 $\mathscr{E}_B$ 的张量积。为了保证属性相同,$\mathscr{E}_A$ 与 $\mathscr{E}_B$、$\mathscr{E}_I$ 互相自然同构。若入射光子的态矢量为 $ \left\lvert \chi \right\rangle $,出射的 $A$ 光子的态矢量为 $ \left\lvert \psi \right\rangle $、出射的 $B$ 光子的态矢量为 $ \left\lvert \phi \right\rangle $,则 $ \left\lvert \chi \right\rangle $、$ \left\lvert \psi \right\rangle $、$ \left\lvert \phi \right\rangle $ 应当在同构映射的意义下彼此相等(或相差一个无意义的相位因子)。从而,经过 $BBO$ 晶体后,整个体系的态矢量应当为
\begin{equation}
\left\lvert \Psi(t=0) \right\rangle =\alpha \left\lvert \psi_L(t=0) \right\rangle \left\lvert \phi_L(t=0) \right\rangle +\beta \left\lvert \psi_R(t=0) \right\rangle \left\lvert \phi_R(t=0) \right\rangle ~.
\end{equation}
其中 $ \left\lvert \psi_L(t=0) \right\rangle $ 是与 $ \left\lvert \chi_L(t=0) \right\rangle $ 在同构映射的意义下相等的矢量,$ \left\lvert \psi_R(t=0) \right\rangle $、$ \left\lvert \phi_L(t=0) \right\rangle $、$ \left\lvert \phi_R(t=0) \right\rangle $ 的定义同理。这里没有考虑自旋态空间,实际上这对后面的解释没有实质性影响。请读者想一想为什么?
现在考虑体系的演化。在射出 $BBO$ 晶体后,$A$ 光子和 $B$ 光子将各自独立地演化,因此体系的哈密顿算符是这两者各自的哈密顿算符(的延伸算符)之和,即 $H=H_A+H_B$。假定 $ \left\lvert \psi_L(t) \right\rangle $ 是满足下列薛定谔方程的解:
\begin{equation}
\mathrm{i} \hbar\frac{ \,\mathrm{d}{}} { \,\mathrm{d}{t} } \left\lvert \psi_L \right\rangle =H_A \left\lvert \psi_L \right\rangle ~.
\end{equation}
该解的初态即为 $ \left\lvert \psi_L(t=0) \right\rangle $。同理,对 $ \left\lvert \psi_R(t) \right\rangle $、$ \left\lvert \phi_L(t) \right\rangle $、$ \left\lvert \phi_R(t) \right\rangle $ 也作同样的假定。于是,任意时刻整个体系的态可以写作
\begin{equation}
\left\lvert \Psi(t) \right\rangle =\alpha \left\lvert \psi_L(t) \right\rangle \left\lvert \phi_L(t) \right\rangle +\beta \left\lvert \psi_R(t) \right\rangle \left\lvert \phi_R(t) \right\rangle ~.
\end{equation}
这是因为这样定义的 $ \left\lvert \Psi(t) \right\rangle $ 满足整个体系的薛定谔方程:
\begin{align}
& \mathrm{i} \hbar\frac{ \,\mathrm{d}{}} { \,\mathrm{d}{t} } \left\lvert \Psi(t) \right\rangle \notag \\
={}&\alpha(( \mathrm{i} \hbar\frac{ \,\mathrm{d}{}} { \,\mathrm{d}{t} } \left\lvert \psi_L(t) \right\rangle ) \left\lvert \phi_L(t) \right\rangle + \left\lvert \psi_L(t) \right\rangle ( \mathrm{i} \hbar\frac{ \,\mathrm{d}{}} { \,\mathrm{d}{t} } \left\lvert \phi_L(t) \right\rangle )) \notag \\
&+\beta(( \mathrm{i} \hbar\frac{ \,\mathrm{d}{}} { \,\mathrm{d}{t} } \left\lvert \psi_R(t) \right\rangle ) \left\lvert \phi_R(t) \right\rangle + \left\lvert \psi_R(t) \right\rangle ( \mathrm{i} \hbar\frac{ \,\mathrm{d}{}} { \,\mathrm{d}{t} } \left\lvert \phi_R(t) \right\rangle )) \notag \\
={}&\alpha(H_A \left\lvert \psi_L(t) \right\rangle \left\lvert \phi_L(t) \right\rangle + \left\lvert \psi_L(t) \right\rangle H_B \left\lvert \phi_L(t) \right\rangle ) \notag \\
&+\beta(H_A \left\lvert \psi_R(t) \right\rangle \left\lvert \phi_R(t) \right\rangle + \left\lvert \psi_R(t) \right\rangle H_B \left\lvert \phi_R(t) \right\rangle ) \notag \\
={}&H \left\lvert \Psi(t) \right\rangle ~.
\end{align}
哈密顿量各自独立,态矢量当然是互相独立地演化。这样体系的演化就得到了求解。为简化讨论,再对体系的演化提出以下假设:
(i)所有的态都是已归一化的。
(ii)$B$ 光子的波函数在 $BS_c$ 之前的路径上是不重叠的,即 $\phi_L(\boldsymbol{r_B},t)\phi_R(\boldsymbol{r_B},t)$ 在路径上恒为零。
(iii)$A$ 光子与 $B$ 光子的波函数分布范围足够小,使得在屏幕后面探测不到光子,也即不会出现光子从屏幕外面经过的情况。
屏幕对光子的作用相当于进行了一次位置的测量,这会导致态矢量发生跃变。假设在 $t_A$ 时刻屏幕 $D_0$ 感光,在 $t_B$ 时刻 $D_1$、$D_2$、$D_3$、$D_4$ 中的任意一个感光。一般 $t_B>t_A$,也就是说屏幕 $D_0$ 先感光,另外四个屏幕再感光。下面假设 $t_A=t_B$,这样会给计算带来方便,也不会给解释问题带来实质性影响。如果不这样假设,将会涉及到态矢量的跃变等问题,较难处理,作者以后可能会补上这一内容。
3. 对实验结果的解释
现在只看 $D_0$ 上的落点分布而不关注另外四个感光屏上出现的现象,则 $A$ 的位置分布就是概率关于 $\boldsymbol{r_A}$ 的边缘分布。联合概率分布为
\begin{align}
&\rho(\boldsymbol{r_A},\boldsymbol{r_B}) \notag \\
={}&|\alpha\psi_L(\boldsymbol{r_A},t_A)\phi_L(\boldsymbol{r_B},t_A)+\beta\psi_R(\boldsymbol{r_A},t_A)\phi_R(\boldsymbol{r_B},t_A)|^2 \notag \\
={}&|\alpha|^2|\psi_L(\boldsymbol{r_A},t_A)|^2|\phi_L(\boldsymbol{r_B},t_A)|^2 \notag \\
&+|\beta|^2|\psi_R(\boldsymbol{r_A},t_A)|^2|\phi_R(\boldsymbol{r_B},t_A)|^2 \notag \\
&+2Re(\alpha\beta^*\psi_L(\boldsymbol{r_A},t_A)\psi_R^*(\boldsymbol{r_A},t_A)\phi_L(\boldsymbol{r_B},t_A)\phi_R^*(\boldsymbol{r_B},t_A))~.
\end{align}
对 $\boldsymbol{r_B}$ 积分得到关于 $\boldsymbol{r_A}$ 的边缘概率分布。考虑到 $ \left\lvert \phi_L \right\rangle $ 和 $ \left\lvert \phi_R \right\rangle $ 都是归一化的态,可得
\begin{align}
&\rho_A(\boldsymbol{r_A}) \notag \\
={}&\int \rho(\boldsymbol{r_A},\boldsymbol{r_B}) \,\mathrm{d}{} ^3\boldsymbol{r_B} \notag \\
={}&|\alpha|^2|\psi_L(\boldsymbol{r_A},t_A)|^2+|\beta|^2|\psi_R(\boldsymbol{r_A},t_A)|^2 \notag \\
&+2Re(\alpha\beta^*\psi_L(\boldsymbol{r_A},t_A)\psi_R^*(\boldsymbol{r_A},t_A) \left\langle \phi_R(t_A) \middle| \phi_L(t_A) \right\rangle )~.
\end{align}
注意到薛定谔方程是保内积的,即
\begin{align}
& \mathrm{i} \hbar\frac{ \,\mathrm{d}{}} { \,\mathrm{d}{t} } \left\langle \xi \middle| \eta \right\rangle \notag \\
={}& \mathrm{i} \hbar(\frac{ \,\mathrm{d}{}} { \,\mathrm{d}{t} } \left\langle \xi \right\rvert ) \left\lvert \eta \right\rangle + \mathrm{i} \hbar \left\langle \xi \right\rvert (\frac{ \,\mathrm{d}{}} { \,\mathrm{d}{t} } \left\lvert \eta \right\rangle ) \notag \\
={}&- \left\langle \xi \right\rvert H \left\lvert \eta \right\rangle + \left\langle \xi \right\rvert H \left\lvert \eta \right\rangle \notag \\
={}&0~.
\end{align}
而 $ \left\lvert \phi_L \right\rangle $ 和 $ \left\lvert \phi_R \right\rangle $ 两个态初始时就是正交的,于是得 $A$ 光子的总分布
\begin{equation}
\rho_A(\boldsymbol{r_A})=|\alpha|^2|\psi_L(\boldsymbol{r_A},t_A)|^2+|\beta|^2|\psi_R(\boldsymbol{r_A},t_A)|^2~.
\end{equation}
注意,$|\psi_L(\boldsymbol{r_A},t_A)|^2$ 是 $L$ 类分布,$|\psi_R(\boldsymbol{r_A},t_A)|^2$ 是 $R$ 类分布。于是实验现象(i)和(v)得到解释。
如果 $D_3$ 或 $D_4$ 感光,$D_0$ 上的光强分布函数就是 $D_3$ 或 $D_4$ 感光时 $A$ 光子关于 $\boldsymbol{r_A}$ 的条件概率分布。以 $D_3$ 感光为例,记 $D_3$ 屏幕的空间区域为 $\Sigma(D_3)$。根据上面的假设,显然有 $\phi_R(\boldsymbol{r_B}\in\Sigma(D_3),t_B)\neq 0$ 且 $\phi_L(\boldsymbol{r_B}\in\Sigma(D_3),t_B)=0$。与式 24 (本应为式 9,但编译器自动生成为式 24)同理,光子 $B$ 的边缘分布为 $\rho_B(\boldsymbol{r_B})=|\alpha|^2|\phi_L(\boldsymbol{r_B},t_B)|^2+|\beta|^2|\phi_R(\boldsymbol{r_B},t_B)|^2$。于是在 $D_3$ 感光的条件下,$A$ 光子的概率分布为:
\begin{align}
&\rho_{A|B}(\boldsymbol{r_A}|\boldsymbol{r_B}\in\Sigma(D_3)) \notag \\
={}&\frac{\int_{\Sigma(D_3)}\rho(\boldsymbol{r_A},\boldsymbol{r_B}) \,\mathrm{d}{} ^3\boldsymbol{r_B}}{\int_{\Sigma(D_3)}\rho_B(\boldsymbol{r_B}) \,\mathrm{d}{} ^3\boldsymbol{r_B}} \notag \\
={}&\frac{|\beta|^2|\psi_R(\boldsymbol{r_A},t_A)|^2\int_{\Sigma(D_3)}|\phi_R(\boldsymbol{r_B},t_A)|^2 \,\mathrm{d}{} ^3\boldsymbol{r_B}}{|\beta|^2\int_{\Sigma(D_3)}|\phi_R(\boldsymbol{r_B},t_A)|^2 \,\mathrm{d}{} ^3\boldsymbol{r_B}} \notag \\
={}&|\psi_R(\boldsymbol{r_A},t_A)|^2~.
\end{align}
$D_4$ 感光的情况也是同理的。于是实验现象(iii)和(iv)得到解释。
如果 $D_1$ 或 $D_2$ 感光,$D_0$ 上的光强分布函数就是 $D_1$ 或 $D_2$ 感光时 $A$ 光子关于 $\boldsymbol{r_A}$ 的条件概率分布。以 $D_1$ 感光为例,记 $D_1$ 屏幕的空间区域为 $\Sigma(D_1)$。根据上面的假设,显然有 $\phi_L(\boldsymbol{r_B}\in\Sigma(D_1),t_B)\neq 0$ 和 $\phi_R(\boldsymbol{r_B}\in\Sigma(D_1),t_B)\neq 0$。令
\begin{equation}
\begin{cases}
\mathscr{I}_1=\int_{\Sigma(D_1)}|\phi_L(\boldsymbol{r_B},t_B)|^2 \,\mathrm{d}{} ^3\boldsymbol{r_B}~; \\
\mathscr{I}_2=\int_{\Sigma(D_1)}|\phi_R(\boldsymbol{r_B},t_B)|^2 \,\mathrm{d}{} ^3\boldsymbol{r_B}~; \\
\mathscr{I}_3=\int_{\Sigma(D_1)}\phi_L(\boldsymbol{r_B},t_B)\phi_R^*(\boldsymbol{r_B},t_B) \,\mathrm{d}{} ^3\boldsymbol{r_B}~.
\end{cases}
\end{equation}
于是在 $D_1$ 感光的条件下,$A$ 光子的概率分布为:
\begin{align}
&\rho_{A|B}(\boldsymbol{r_A}|\boldsymbol{r_B}\in\Sigma(D_1)) \notag \\
={}&\frac{\int_{\Sigma(D_1)}\rho(\boldsymbol{r_A},\boldsymbol{r_B}) \,\mathrm{d}{} ^3\boldsymbol{r_B}}{\int_{\Sigma(D_1)}\rho_B(\boldsymbol{r_B}) \,\mathrm{d}{} ^3\boldsymbol{r_B}} \notag \\
={}&\frac{|\alpha|^2\mathscr{I}_1|\psi_L(\boldsymbol{r_A},t_A)|^2+|\beta|^2\mathscr{I}_2|\psi_R(\boldsymbol{r_A},t_A)}{|\alpha|^2\mathscr{I}_1+|\beta|^2\mathscr{I}_2} \notag \\
&+\frac{2Re(\alpha\beta^*\mathscr{I}_3\psi_L(\boldsymbol{r_A},t_A)\psi_R^*(\boldsymbol{r_A},t_A))}{|\alpha|^2\mathscr{I}_1+|\beta|^2\mathscr{I}_2}~.
\end{align}
虽然 $ \left\langle \psi_R \middle| \psi_L \right\rangle =0$,也即 $\psi_L\psi_R^*$ 在全空间的积分为零,但是一般而言 $\mathscr{I}_3\neq 0$,因此干涉项存在。于是实验现象(ii)得到解释。
4. 相关讨论
由式 11 (本应为式 6,但编译器自动生成为式 11)可知,干涉项始终存在,但是某些观测方式会将干涉项消去。其实,干涉发生在两个光子之间,上述实验中的纠缠状态导致一个光子无法与自己发生干涉,因为它的路径信息被另一个光子泄露出去了。或许可以用一种粗糙的方式来理解这个问题。微观粒子未被观测时具有波粒二象性;一旦被观测,它就必须显示出明显的粒子性或波动性,而不能两者兼有。当观测到路径信息以后,它就具有了粒子性,因而不可能出现干涉条纹之类的波动性产物。若光子的路径信息被纠缠光子泄露,则实验人员时刻都可以通过观测纠缠光子来获知光子的路径信息。即使当前时刻还没有进行观测,但光子具有被观测的 “风险”。试想,如果光子先表现出了波动性,而后实验人员又获知了光子的路径信息,那么光子就同时具有粒子性和波动性了,这就违背了自然规律。自然界为了避免这种情况的发生,就不得不要求光子不能表现波动性。若 $D_1$ 或 $D_2$ 感光,自然界就可以肯定没有人能获知光子的路径信息,所以光子被允许表现出波动性,从而 $1$ 类分布与 $2$ 类分布中存在干涉项。
人们曾经提出这样的想法来刁难自然界:连续发射许多光子,先观测 $D_0$ 上是否具有干涉条纹,如果有就立即(“立即” 的含义是,在 $B$ 光子到达虚线方框之前进行操作)将 $BS_a$ 和 $BS_b$ 换成全反射镜,如果没有干涉条纹就立即将 $BS_a$ 和 $BS_b$ 去掉。这样一来,当有干涉条纹时,$B$ 光子将会被 $D_3$ 或 $D_4$ 探测到,进而可以获知光子经过了哪条狭缝,这导致获知光子路径和出现干涉条纹这两件矛盾的事同时发生;如果没有干涉条纹,$B$ 光子将会被 $D_1$ 或 $D_2$ 探测到,于是无从知道光子的路径,这导致光子的波动性平白无故地消失。这将是相当诡异的。为了弥补这个自然界的漏洞,人们又想出了一个解释。光子可以预判人类未来是否将会对其的路径信息进行观测,并由此决定自己的行为。读者可以自行上网搜索此实验的相关科普文章,会发现 “量子力学违反因果律” 等说法,正是出自于此。如果人类将要观测,那么光子就让干涉条纹消失;否则,就发生干涉。这种解释显然行不通,但似乎又没有别的更好的解释。事实上,以上这些想法就是人们对量子纠缠认识尚不深刻时提出的,这也是本实验名称的来源。
后来,人们发现,根本不会出现以上那些诡异的现象,因为如果只看 $D_0$,将不可能看到任何干涉条纹。由式 24 (本应为式 9,但编译器自动生成为式 24)可以发现,不论后面对纠缠光子进行什么操作,$A$ 光子的概率分布中都没有干涉项。如果后面选择对光子的路径信息进行擦除,也就是将 $BS_a$ 和 $BS_b$ 去掉,就可以在 $1$ 类分布图与 $2$ 类分布图中分别看到干涉条纹。但是,这种方法仅能对 $1$ 类路径和 $2$ 类路径分别进行擦除,所以总分布仍然没有干涉条纹。至此,所有的矛盾都能顺利得到解释了。