拉格朗日力学 (综述)
贡献者: 待更新
本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章)
在物理学中,拉格朗日力学是一种基于平稳作用原理(也称为最小作用原理)的经典力学表述。它由意大利-法国数学家和天文学家约瑟夫-路易·拉格朗日在 1760 年向都灵科学学院的演讲中提出,并在 1788 年他的巨著《解析力学》中达到巅峰。
拉格朗日力学将一个力学系统描述为由构型空间 \( M \) 和其中的一个光滑函数 \( L \)(称为拉格朗日量)组成的对 \( (M, L) \)。对于许多系统,\( L = T - V \),其中 \( T \) 和 \( V \) 分别为系统的动能和势能。
平稳作用原理要求由 \( L \) 推导出的系统的作用泛函在系统的时间演化过程中保持在一个平稳点(最大值、最小值或鞍点)。这一约束条件使得可以利用拉格朗日方程计算系统的运动方程。
1. 简介
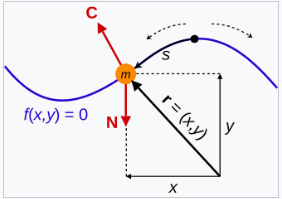
一个珠子被限制在无摩擦的细线上运动。细线对珠子施加一个反作用力 \( C \),以保持其在细线上。此时的非约束力 \( N \) 是重力。注意,珠子在细线上的初始位置可能会导致不同的运动。
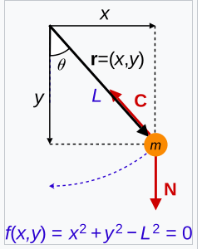
简单摆。由于杆是刚性的,摆锤的位置受到方程 \( f(x, y) = 0 \) 的约束,约束力 \( C \) 是杆中的拉力。同样,此时的非约束力 \( N \) 也是重力。
牛顿定律和力的概念通常是讲授机械系统的起点【5】。这种方法适用于许多问题,但对于一些问题,计算变得极其复杂【6】。例如,在计算一个带珍珠的圆环在水平面上滚动的运动时,时间变化的约束力(例如圆环的角速度、珍珠相对于圆环的运动)使得利用牛顿方程难以确定圆环的运动【7】。拉格朗日力学采用能量而非力作为基本成分【5】,从而得到更抽象的方程,能够处理更复杂的问题【6】。
特别是,拉格朗日的方法是为每个物体的位移和速度建立独立的广义坐标,从而写出一个拉格朗日量(系统的总动能减去势能)的通式,并对所有可能的粒子运动路径进行求和,得到‘作用’的公式,通过极小化作用得到一组广义方程。这一求和的量在粒子实际采取的路径上被最小化。这一选择消除了将约束力引入最终广义方程组的必要性。这样,方程减少了,因为不需要直接计算给定时刻约束对粒子的影响【7】。
对于各种物理系统,如果一个物体的大小和形状可以忽略不计,将其视为质点是一种有用的简化。对于由质量为 \( m_1, m_2, \dots, m_N \) 的 \( N \) 个质点组成的系统,每个质点都有一个位置向量,分别记为 \( r_1, r_2, \dots, r_N \)。笛卡尔坐标系通常足够,因此 \( r_1 = (x_1, y_1, z_1), r_2 = (x_2, y_2, z_2) \) 等。在三维空间中,每个位置向量需要三个坐标来唯一确定一个点的位置,因此需要 \( 3N \) 个坐标来唯一确定系统的构型。这些坐标是粒子在空间中的具体位置;空间中的一个通用点写作 \( r = (x, y, z) \)。每个粒子的速度是其沿运动路径的移动速度,为其位置的时间导数,因此 \[ \mathbf{v}_1 = \frac{d\mathbf{r}_1}{dt}, \quad \mathbf{v}_2 = \frac{d\mathbf{r}_2}{dt}, \dots, \quad \mathbf{v}_N = \frac{d\mathbf{r}_N}{dt}.~ \] 在牛顿力学中,运动方程由牛顿定律给出。第二定律 “合力等于质量乘加速度” 适用于每个粒子, \[ \sum \mathbf{F} = m \frac{d^2 \mathbf{r}}{dt^2},~ \] 对于一个三维的 \( N \) 粒子系统,这样的方程组成了关于粒子位置的 \( 3N \) 个二阶常微分方程,需要求解。
拉格朗日量
拉格朗日力学不使用力,而是利用系统中的能量。拉格朗日力学的核心量是拉格朗日量,它是一个总结整个系统动力学的函数。总体而言,拉格朗日量的单位是能量,但对于所有物理系统没有统一的表达式。任何能够生成符合物理定律的正确运动方程的函数都可以作为拉格朗日量。然而,可以构建适用于广泛应用的通用表达式。对于没有电磁场的非相对论质点系统,其拉格朗日量为【8】 \[ L = T - V,~ \] 其中 \[ T = \frac{1}{2} \sum_{k=1}^{N} m_k v_k^2~ \] 是系统的总动能,等于 \( N \) 个质点动能之和。每个标记为 \( k \) 的质点具有质量 \( m_k \),且 \( v_k^2 = v_k \cdot v_k \) 是其速度的平方,即速度与自身的点积【9】。
动能 \( T \) 是系统运动的能量,仅依赖于速度 \( v_k \),而不依赖于位置 \( r_k \) 或时间 \( t \),因此 \( T = T(v_1, v_2, \dots) \)。
\( V \) 是系统的势能,反映了粒子之间相互作用的能量,即每个粒子由于其他粒子以及任何外部影响而具有的能量。对于保守力(例如牛顿引力),它仅是粒子位置向量的函数,因此 \( V = V(r_1, r_2, \dots) \)。对于那些可以从适当的势中导出的非保守力(例如电磁势),势能也会涉及速度,即 \( V = V(r_1, r_2, \dots, v_1, v_2, \dots) \)。如果存在随时间变化的外场或外部驱动力,势能也会随时间变化,因此最普遍地表示为 \( V = V(r_1, r_2, \dots, v_1, v_2, \dots, t) \)。
如前所述,这种形式的 \( L \) 适用于许多重要的系统类型,但并不适用于所有情况。对于相对论拉格朗日力学,必须用一个与狭义相对论(在洛伦兹变换下为标量)或广义相对论(4-标量)一致的函数来替代【10】。如果存在磁场,则需要重新表述势能的表达式【需要引用】。对于耗散力(例如摩擦),通常需要引入一个称为 “瑞利耗散函数” 的函数来描述能量损失【11】。
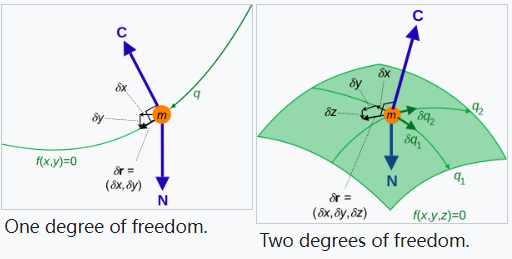
一个或多个粒子可能会受到一个或多个完整约束的限制;这种约束由形式 \( f(r, t) = 0 \) 的方程描述。如果系统中有 \( C \) 个约束,那么每个约束都有一个方程 \( f_1(r, t) = 0, f_2(r, t) = 0, \dots, f_C(r, t) = 0 \),这些方程可以应用于任何粒子。如果粒子 \( k \) 受到约束 \( i \) 的限制,则 \( f_i(r_k, t) = 0 \)。在任何时刻,受约束粒子的坐标是相互关联的,而不是独立的。约束方程决定了粒子可以沿着哪些路径运动,但并不规定它们的确切位置或速度。非完整约束依赖于粒子的速度、加速度或位置的更高阶导数。拉格朗日力学仅适用于所有约束都是完整的系统。三个非完整约束的例子为【12】。
当约束方程是不可积的、约束具有不等式、或存在诸如摩擦之类复杂的非保守力时,需要特殊处理非完整约束,可能需要回归到牛顿力学或使用其他方法【13】。
如果由于时间变化的约束或外部影响使得 \( T \) 或 \( V \) 或两者都显式地依赖于时间,则拉格朗日量 \( L(r_1, r_2, \dots, v_1, v_2, \dots, t) \) 显式地依赖于时间。如果势能和动能都不依赖于时间,那么拉格朗日量 \( L(r_1, r_2, \dots, v_1, v_2, \dots) \) 显式地与时间无关。在这两种情况下,拉格朗日量始终通过广义坐标隐含地依赖于时间。
根据这些定义,拉格朗日第一类方程为[14]:
拉格朗日方程(第一类) \[ \frac{\partial L}{\partial \mathbf{r}_{k}} - \frac{\mathrm{d}}{\mathrm{d}t} \frac{\partial L}{\partial \dot{\mathbf{r}}_{k}} + \sum_{i=1}^{C} \lambda_{i} \frac{\partial f_{i}}{\partial \mathbf{r}_{k}} = 0,~ \] 其中 \( k = 1, 2, \ldots, N \) 表示粒子,\(\lambda_{i}\) 是每个约束方程 \( f_{i} \) 的拉格朗日乘子,且 \[ \frac{\partial }{\partial \mathbf{r}_{k}} \equiv \left(\frac{\partial }{\partial x_{k}}, \frac{\partial }{\partial y_{k}}, \frac{\partial }{\partial z_{k}}\right), \quad \frac{\partial }{\partial \dot{\mathbf{r}}_{k}} \equiv \left(\frac{\partial }{\partial \dot{x}_{k}}, \frac{\partial }{\partial \dot{y}_{k}}, \frac{\partial }{\partial \dot{z}_{k}}\right)~ \] 是对指定变量的偏导数的简写(而不是对整个向量的导数)。每个点上方的符号表示时间导数。与牛顿定律相比,这种方法确实增加了需要解决的方程数量,从 \( 3N \) 增加到 \( 3N + C \),因为在位置坐标和乘子中有 \( 3N \) 个耦合的二阶微分方程,以及 \( C \) 个约束方程。然而,当与粒子的位置信息一起求解时,乘子可以提供关于约束力的信息。坐标不需要通过求解约束方程来消去。
在拉格朗日函数中,位置坐标和速度分量都是独立变量,拉格朗日函数的导数是根据通常的微分规则分别对这些变量进行求导的(例如,对于粒子 2 的 z 方向速度分量,定义为 \(v_{z,2} = \frac{dz_2}{dt}\),其偏导数 \(\frac{\partial L}{\partial v_{z,2}}\) 就是所需的;不需要使用复杂的链式法则或全导数来将速度分量与相应的坐标 \(z_2\) 关联)。
在每个约束方程中,一个坐标是多余的,因为它是由其他坐标确定的。因此,独立坐标的数量为 \(n = 3N - C\)。我们可以将每个位置向量转换为一组公共的 \(n\) 个广义坐标,方便地写成 \(n\)-元组 \(q = (q_1, q_2, ... q_n)\),通过将每个位置向量,进而每个位置坐标,表示为广义坐标和时间的函数: \[ \mathbf{r}_{k} = \mathbf{r}_{k}(\mathbf{q}, t) = {\big (}x_{k}(\mathbf{q}, t), y_{k}(\mathbf{q}, t), z_{k}(\mathbf{q}, t), t{\big )}.~ \] 根据这些定义,欧拉–拉格朗日方程,或称为第二类拉格朗日方程[15][16][17]:
拉格朗日方程(第二类) \[ \frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\partial L}{\partial \dot{q}_j}\right) = \frac{\partial L}{\partial q_j}~ \] 是变分法的数学结果,也可以应用于力学。将拉格朗日函数 \(L(q, \frac{dq}{dt}, t)\) 代入其中,可以得到系统的运动方程。与牛顿力学相比,方程的数量从 \(3N\) 减少到 \(n = 3N - C\) 个耦合的二阶微分方程,采用广义坐标。这些方程完全不包括约束力,仅需考虑非约束力。
虽然运动方程包含偏导数,但这些偏导数的结果仍然是粒子位置坐标的常微分方程。表示为 \(\frac{d}{dt}\) 的全时间导数通常涉及隐式微分。这两个方程在拉格朗日函数中是线性的,但在坐标中通常是非线性耦合方程。
2. 从牛顿力学到拉格朗日力学
牛顿定律
为了简单起见,牛顿定律可以在不失一般性的情况下针对一个粒子进行说明(对于一个由 \(N\) 个粒子组成的系统,这些方程同样适用于系统中的每个粒子)。对于质量为 \(m\) 的粒子,其运动方程是 1687 年牛顿的第二定律,用现代向量符号表示为 \[ \mathbf{F} = m \mathbf{a},~ \] 其中 \(a\) 是加速度,\(F\) 是作用在其上的合力。当质量变化时,该方程需要推广,以考虑动量的时间导数。在三维空间中,这是一个由三个耦合的二阶常微分方程组成的系统,因为这个向量方程中有三个分量。其解为粒子在时间 \(t\) 的位置向量 \(r\),受初始条件 \(r\) 和 \(v\) 在 \(t = 0\) 时的约束。
牛顿定律在笛卡尔坐标系中容易使用,但笛卡尔坐标并不总是方便,对于其他坐标系,运动方程可能变得复杂。在一组曲线坐标 \(\xi = (\xi_1, \xi_2, \xi_3)\) 中,以张量指标符号表示的定律是 “拉格朗日形式”[18][19]: \[ F^{a} = m\left(\frac{\mathrm{d}^{2}\xi^{a}}{\mathrm{d}t^{2}} + \Gamma^{a}{}_{bc} \frac{\mathrm{d}\xi^{b}}{\mathrm{d}t} \frac{\mathrm{d}\xi^{c}}{\mathrm{d}t}\right) = g^{ak}\left(\frac{\mathrm{d}}{\mathrm{d}t} \frac{\partial T}{\partial \dot{\xi}^{k}} - \frac{\partial T}{\partial \xi^{k}}\right), \quad \dot{\xi}^{a} \equiv \frac{\mathrm{d}\xi^{a}}{\mathrm{d}t},~ \] 其中 \(F^{a}\) 是作用在粒子上的合力的第 \(a\) 个协变分量,\(\Gamma^{abc}\) 是第二类克里斯托费尔符号, \[ T = \frac{1}{2}mg_{bc} \frac{\mathrm{d}\xi^{b}}{\mathrm{d}t} \frac{\mathrm{d}\xi^{c}}{\mathrm{d}t}~ \] 是粒子的动能,\(g_{bc}\) 是曲线坐标系的度量张量的协变分量。所有指标 \(a, b, c\) 都取值 1, 2, 3。曲线坐标与广义坐标并不相同。
将牛顿定律表达成这种形式似乎有些复杂,但这有其优势。通过评估动能的导数,可以避免以克里斯托费尔符号表示的加速度分量。如果作用在粒子上的合力为零,即 \(F = 0\),那么粒子不会加速,而是以恒定速度沿直线运动。从数学上讲,微分方程的解是测地线,即空间中两个点之间的极值长度曲线(这些曲线可能是最短路径,但不一定)。在平坦的三维真实空间中,测地线只是直线。因此,对于自由粒子,牛顿的第二定律与测地线方程一致,表明自由粒子遵循测地线,即它能够沿其移动的极值轨迹。如果粒子受到 \(F \neq 0\) 的力作用,粒子会因作用在其上的力而加速,并偏离它如果是自由粒子时所遵循的测地线。将这里给出的平坦三维空间中的量适当扩展到四维曲率时空,上述形式的牛顿定律也适用于爱因斯坦的广义相对论,在这种情况下,自由粒子在曲率时空中遵循的测地线不再是普通意义上的 “直线”[20]。
然而,我们仍需要知道作用在粒子上的总合力 \(F\),这反过来需要非约束力的合力 \(N\) 加上约束力的合力 \(C\), \[ \mathbf{F} = \mathbf{C} + \mathbf{N}.~ \] 约束力可能很复杂,因为它们通常依赖于时间。此外,如果存在约束,曲线坐标并不是独立的,而是通过一个或多个约束方程相互关联。
可以通过将约束力从运动方程中消除,使得只剩下非约束力,或者通过在运动方程中包含约束方程来包含约束力。
达朗贝尔原理
分析力学中的一个基本结果是达朗贝尔原理,该原理由雅克·伯努利于 1708 年提出,用于理解静态平衡,并由达朗贝尔于 1743 年发展以解决动力学问题[21]。该原理断言,对于 \(N\) 个粒子,虚功,即沿虚位移 \(\delta \mathbf{r}_k\) 的功,为零[9]: \[ \sum_{k=1}^{N}(\mathbf{N}_{k}+\mathbf{C}_{k}-m_{k}\mathbf{a}_{k}) \cdot \delta \mathbf{r}_{k} = 0.~ \]
虚位移 \(\delta \mathbf{r}_k\) 根据定义是与在某一时刻作用于系统的约束力一致的系统配置的微小变化[22],即以这样的方式,使得约束力维持受约束的运动。它们与系统中的实际位移不同,实际位移是由作用在粒子上的合成约束力和非约束力引起的,以使其加速并移动。虚功是沿虚位移所做的功,无论是对于约束力还是非约束力。
由于约束力作用于系统中每个粒子的运动方向垂直,以维持约束,因此作用于系统的约束力所做的总虚功为零: \[ \sum_{k=1}^{N} \mathbf{C}_{k} \cdot \delta \mathbf{r}_{k} = 0,~ \] 因此有 \[ \sum_{k=1}^{N} (\mathbf{N}_{k} - m_{k} \mathbf{a}_{k}) \cdot \delta \mathbf{r}_{k} = 0.~ \] 因此,达朗贝尔原理使我们能够只关注施加的非约束力,并在运动方程中排除约束力[24][25]。所示的形式也独立于坐标的选择。然而,它不能直接用于在任意坐标系中建立运动方程,因为虚位移 \(\delta \mathbf{r}_k\) 可能通过约束方程相连,这阻止我们将 \(N\) 个单项和设为零。因此,我们将寻求一组相互独立的坐标,对于这些坐标,只有当每个单项和为零时,总和才为零。将每个单项和设为零最终将给我们分开的运动方程。
从达朗贝尔原理得到的运动方程
如果对粒子 \(k\) 存在约束,那么由于位置坐标 \( \mathbf{r}_k = (x_k, y_k, z_k) \) 通过约束方程相互关联,虚位移 \( \delta \mathbf{r}_k = (\delta x_k, \delta y_k, \delta z_k) \) 也是如此。由于广义坐标是独立的,我们可以通过转换为广义坐标中的虚位移来避免与 \( \delta \mathbf{r}_k \) 相关的复杂性。这些虚位移以与全导数相同的形式相关联,[9]: \[ \delta \mathbf{r}_k = \sum_{j=1}^{n} \frac{\partial \mathbf{r}_k}{\partial q_j} \delta q_j.~ \] 这里没有相对于时间的偏导数与时间增量相乘,因为这是一个虚位移,沿着约束在某一时刻的位移。
达朗贝尔原理中的第一项是非约束力 \( \mathbf{N}_k \) 沿虚位移 \( \delta \mathbf{r}_k \) 所做的虚功,可以在不失一般性的情况下通过广义力的定义转换为广义模拟: \[ Q_j = \sum_{k=1}^{N} \mathbf{N}_k \cdot \frac{\partial \mathbf{r}_k}{\partial q_j},~ \] 因此有 \[ \sum_{k=1}^{N} \mathbf{N}_k \cdot \delta \mathbf{r}_k = \sum_{k=1}^{N} \mathbf{N}_k \cdot \sum_{j=1}^{n} \frac{\partial \mathbf{r}_k}{\partial q_j} \delta q_j = \sum_{j=1}^{n} Q_j \delta q_j.~ \] 这是转换为广义坐标的一半。接下来需要将加速度项转换为广义坐标,这一点并不明显。回想牛顿第二定律的拉格朗日形式,可以找到动能对广义坐标和速度的偏导数,以得到所需的结果[9]: \[ \sum_{k=1}^{N} m_k \mathbf{a}_k \cdot \frac{\partial \mathbf{r}_k}{\partial q_j} = \frac{\mathrm{d}}{\mathrm{d} t} \frac{\partial T}{\partial \dot{q}_j} - \frac{\partial T}{\partial q_j}.~ \] 现在,达朗贝尔原理已经转换为所需的广义坐标: \[ \sum_{j=1}^{n}\left[Q_j - \left(\frac{\mathrm{d}}{\mathrm{d} t} \frac{\partial T}{\partial \dot{q}_j} - \frac{\partial T}{\partial q_j}\right)\right]\delta q_j = 0,~ \] 由于这些虚位移 \(\delta q_j\) 是独立且非零的,因此可以将系数设为零,结果得到拉格朗日方程[26][27]或广义运动方程[28]: \[ Q_{j} = \frac{\mathrm{d}}{\mathrm{d} t} \frac{\partial T}{\partial \dot{q}_{j}} - \frac{\partial T}{\partial q_{j}}.~ \] 这些方程等同于非约束力的牛顿定律。该方程中的广义力仅来源于非约束力——约束力已被排除在达朗贝尔原理之外,无需计算。只要满足达朗贝尔原理,广义力可能是非保守的[29]。
欧拉-拉格朗日方程和汉密尔顿原理
对于依赖于速度的非保守力,可能找到一个依赖于位置和速度的势能函数 \( V \)。如果广义力 \( Q_i \) 可以通过一个势能 \( V \) 得到,使得:[31][32] \[ Q_{j} = \frac{\mathrm{d}}{\mathrm{d} t} \frac{\partial V}{\partial \dot{q}_{j}} - \frac{\partial V}{\partial q_{j}},~ \] 将其与拉格朗日方程相等,并定义拉格朗日量为 \( L = T - V \),得到第二类拉格朗日方程或欧拉-拉格朗日运动方程: \[ \frac{\partial L}{\partial q_{j}} - \frac{\mathrm{d}}{\mathrm{d} t} \frac{\partial L}{\partial \dot{q}_{j}} = 0.~ \] 然而,欧拉-拉格朗日方程只能在能够找到势能的情况下考虑非保守力。对于非保守力,这并不总是可能的,因此拉格朗日方程不涉及任何势能,仅涉及广义力;因此它们比欧拉-拉格朗日方程更为一般。
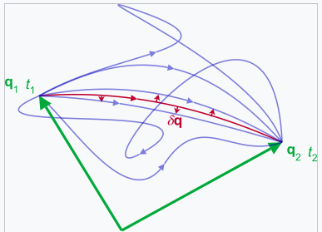
欧拉-拉格朗日方程也源于变分法。拉格朗日量的变化为: \[ \delta L = \sum_{j=1}^{n} \left( \frac{\partial L}{\partial q_{j}} \delta q_{j} + \frac{\partial L}{\partial \dot{q}_{j}} \delta \dot{q}_{j} \right), \quad \delta \dot{q}_{j} \equiv \delta \frac{\mathrm{d} q_{j}}{\mathrm{d} t} \equiv \frac{\mathrm{d} (\delta q_{j})}{\mathrm{d} t},~ \] 这具有类似于 \( L \) 的全微分的形式,但虚位移及其时间导数替代了微分,且根据虚位移的定义,没有时间增量。对时间进行分部积分可以将 \( \delta q_{j} \) 的时间导数转移到 \( \frac{\partial L}{\partial (\frac{dq_{j}}{dt})} \) 上,在此过程中,将 \( \frac{d(\delta q_{j})}{dt} \) 替换为 \( \delta q_{j} \),从而使独立的虚位移可以从拉格朗日量的导数中提取出来: \[ \begin{aligned} \int_{t_{1}}^{t_{2}} \delta L \, \mathrm{d} t &= \int_{t_{1}}^{t_{2}} \sum_{j=1}^{n} \left( \frac{\partial L}{\partial q_{j}} \delta q_{j} + \frac{\mathrm{d}}{\mathrm{d} t} \left( \frac{\partial L}{\partial \dot{q}_{j}} \delta q_{j} \right) - \frac{\mathrm{d}}{\mathrm{d} t} \frac{\partial L}{\partial \dot{q}_{j}} \delta q_{j} \right) \, \mathrm{d} t,\\ &= \sum_{j=1}^{n} \left[ \frac{\partial L}{\partial \dot{q}_{j}} \delta q_{j} \right]_{t_{1}}^{t_{2}} + \int_{t_{1}}^{t_{2}} \sum_{j=1}^{n} \left( \frac{\partial L}{\partial q_{j}} - \frac{\mathrm{d}}{\mathrm{d} t} \frac{\partial L}{\partial \dot{q}_{j}} \right) \delta q_{j} \, \mathrm{d} t. \end{aligned}~ \] 现在,如果对所有 \( j \) 都满足条件 \( \delta q_{j}(t_{1}) = \delta q_{j}(t_{2}) = 0 \),则未积分的项为零。如果此外整个 \( \delta L \) 的时间积分为零,那么由于 \( \delta q_{j} \) 是独立的,唯一使定积分为零的方式是被积函数等于零,因此每个 \( \delta q_{j} \) 的系数也必须为零。这样我们就得到了运动方程。这可以通过哈密顿原理来总结: \[ \int_{t_{1}}^{t_{2}} \delta L \, \mathrm{d} t = 0.~ \] 拉格朗日函数的时间积分是另一个称为作用量的量,定义为[33] \[ S = \int_{t_{1}}^{t_{2}} L \, \mathrm{d} t,~ \] 这是一个泛函;它接收在 \( t_{1} \) 和 \( t_{2} \) 之间所有时刻的拉格朗日函数,并返回一个标量值。它的维度与 [角动量]、[能量]·[时间] 或 [长度]·[动量] 相同。根据这个定义,哈密顿原理为 \[ \delta S = 0.~ \] 与其考虑粒子对施加力的响应而加速,不如将其视为选择具有静止作用的路径,其中路径在配置空间的端点在初始和最终时刻保持固定。哈密顿原理是几种作用原理之一。[34]
历史上,寻找粒子在受力情况下可以遵循的最短路径的想法促使了变分法在机械问题中的首次应用,例如让·伯努利在 1696 年解决的最速降线问题,以及莱布尼茨、丹尼尔·伯努利、洛必达等人大约在同一时期的研究,牛顿在次年也对此进行了思考。[35] 牛顿本人也是在变分法的思路上进行思考,但并未发表。[35] 这些思想进而引出了费马、莫佩尔蒂斯、欧拉、哈密顿等人的力学变分原理。
哈密顿原理可以应用于非保守约束,如果约束方程可以以某种形式表达,即坐标的一阶微分的线性组合。得到的约束方程可以重新排列成一阶微分方程。[36] 这里不再赘述。
拉格朗日乘子和约束
拉格朗日量 \( L \) 可以在 \( N \) 个粒子的笛卡尔坐标 \( \mathbf{r}_k \) 中变化, \[ \int_{t_{1}}^{t_{2}} \sum_{k=1}^{N} \left( \frac{\partial L}{\partial \mathbf{r}_{k}} - \frac{\mathrm{d}}{\mathrm{d} t} \frac{\partial L}{\partial \dot{\mathbf{r}}_{k}} \right) \cdot \delta \mathbf{r}_{k} \,\mathrm{d} t = 0.~ \] 哈密尔顿原理仍然有效,即使拉格朗日量 \( L \) 所表达的坐标 \( \mathbf{r}_k \) 不是独立的,但仍假设约束是全能的。[37] 像往常一样,端点是固定的 \( \delta \mathbf{r}_k(t_1) = \delta \mathbf{r}_k(t_2) = 0 \) 对所有 \( k \) 都成立。不能简单地将 \( \delta \mathbf{r}_k \) 的系数置为零,因为 \( \delta \mathbf{r}_k \) 不是独立的。相反,可以使用拉格朗日乘子法来包含约束。将每个约束方程 \( f_i(\mathbf{r}_k, t) = 0 \) 乘以拉格朗日乘子 \( \lambda_i \)(对于 \( i = 1, 2, \ldots, C \)),并将结果添加到原始拉格朗日量中,得到新的拉格朗日量 \[ L' = L(\mathbf{r}_{1}, \mathbf{r}_{2}, \ldots, \dot{\mathbf{r}}_{1}, \dot{\mathbf{r}}_{2}, \ldots, t) + \sum_{i=1}^{C} \lambda_{i}(t) f_{i}(\mathbf{r}_{k}, t).~ \]
拉格朗日乘子是时间 \( t \) 的任意函数,但不是坐标 \( \mathbf{r}_k \) 的函数,因此乘子与位置坐标处于同等地位。对这个新的拉格朗日量进行变分并对时间积分,得到 \[ \int_{t_{1}}^{t_{2}} \delta L' \, \mathrm{d} t = \int_{t_{1}}^{t_{2}} \sum_{k=1}^{N} \left( \frac{\partial L}{\partial \mathbf{r}_{k}} - \frac{\mathrm{d}}{\mathrm{d} t} \frac{\partial L}{\partial \dot{\mathbf{r}}_{k}} + \sum_{i=1}^{C} \lambda_{i} \frac{\partial f_{i}}{\partial \mathbf{r}_{k}} \right) \cdot \delta \mathbf{r}_{k} \, \mathrm{d} t = 0.~ \] 引入的乘子可以被选择,使得 \( \delta \mathbf{r}_k \) 的系数为零,即使 \( \mathbf{r}_k \) 不是独立的。由此得到运动方程。从前面的分析可知,求解这个积分等价于以下陈述: \[ \frac{\partial L'}{\partial \mathbf{r}_{k}} - \frac{\mathrm{d}}{\mathrm{d} t} \frac{\partial L'}{\partial \dot{\mathbf{r}}_{k}} = 0 \Rightarrow \frac{\partial L}{\partial \mathbf{r}_{k}} - \frac{\mathrm{d}}{\mathrm{d} t} \frac{\partial L}{\partial \dot{\mathbf{r}}_{k}} + \sum_{i=1}^{C} \lambda_{i} \frac{\partial f_{i}}{\partial \mathbf{r}_{k}} = 0,~ \] 这就是拉格朗日的第一类方程。同时,针对新的拉格朗日量的 \( \lambda_i \) 欧拉-拉格朗日方程返回约束方程: \[ \frac{\partial L'}{\partial \lambda_{i}} - \frac{\mathrm{d}}{\mathrm{d} t} \frac{\partial L'}{\partial \dot{\lambda}_{i}} = 0 \Rightarrow f_{i}(\mathbf{r}_{k}, t) = 0.~ \] 对于由某个势能 \( V \) 的梯度给出的保守力,该势能仅依赖于 \( \mathbf{r}_k \) 坐标,将拉格朗日量 \( L = T - V \) 代入,得到 \[ \underbrace{{\frac {\partial T}{\partial \mathbf{r}_{k}}}-{\frac {\mathrm{d}}{\mathrm{d} t}}{\frac {\partial T}{\partial \dot{\mathbf{r}}_{k}}}}_{-\mathbf{F}_{k}} + \underbrace{-{\frac {\partial V}{\partial \mathbf{r}_{k}}}}_{\mathbf{N}_{k}} + \sum_{i=1}^{C} \lambda_{i} \frac{\partial f_{i}}{\partial \mathbf{r}_{k}} = 0,~ \] 并将动能的导数识别为(负的)合力,而势能的导数等于非约束力,因此可以得出约束力为 \[ \mathbf{C}_{k} = \sum_{i=1}^{C} \lambda_{i} \frac{\partial f_{i}}{\partial \mathbf{r}_{k}},~ \] 从而明确给出约束力以约束方程和拉格朗日乘子的形式表示。
3. 拉格朗日量的性质
非唯一性
给定系统的拉格朗日量并不是唯一的。一个拉格朗日量 \( L \) 可以乘以一个非零常数 \( a \) 并加上一个任意常数 \( b \),新的拉格朗日量 \( L' = aL + b \) 将描述与 \( L \) 相同的运动。如果在给定的时间区间 \([t_{\text{st}}, t_{\text{fin}}]\) 上,并且固定端点 \( P_{\text{st}} = q(t_{\text{st}}) \) 和 \( P_{\text{fin}} = q(t_{\text{fin}}) \),则描述相同系统的两个拉格朗日量可以通过一个函数 \( f(q, t) \) 的 “总时间导数” 相差:[38] \[ L'(\mathbf{q}, \dot{\mathbf{q}}, t) = L(\mathbf{q}, \dot{\mathbf{q}}, t) + \frac{\mathrm{d} f(\mathbf{q}, t)}{\mathrm{d} t},~ \] 其中 \[ \frac{\mathrm{d} f(\mathbf{q}, t)}{\mathrm{d} t} \text{ 表示 } \frac{\partial f(\mathbf{q}, t)}{\partial t} + \sum_{i} \frac{\partial f(\mathbf{q}, t)}{\partial q_{i}} \dot{q}_{i}.~ \] 两个拉格朗日量 \( L \) 和 \( L' \) 产生相同的运动方程[39][40],因为对应的作用量 \( S \) 和 \( S' \) 通过以下关系相连: \[ \begin{aligned} S'[\mathbf{q}] &= \int_{t_{\text{st}}}^{t_{\text{fin}}} L'(\mathbf{q}(t), \dot{\mathbf{q}}(t), t) \, dt \\ &= \int_{t_{\text{st}}}^{t_{\text{fin}}} L(\mathbf{q}(t), \dot{\mathbf{q}}(t), t) \, dt + \int_{t_{\text{st}}}^{t_{\text{fin}}} \frac{\mathrm{d} f(\mathbf{q}(t), t)}{\mathrm{d} t} \, dt \\ &= S[\mathbf{q}] + f(P_{\text{fin}}, t_{\text{fin}}) - f(P_{\text{st}}, t_{\text{st}}), \end{aligned}~ \] 最后两个项 \( f(P_{\text{fin}}, t_{\text{fin}}) \) 和 \( f(P_{\text{st}}, t_{\text{st}}) \) 与 \( q \) 无关。
在点变换下的不变性
给定一组广义坐标 \( q \),如果我们根据可逆的点变换 \( Q = Q(q, t) \) 将这些变量更改为一组新的广义坐标 \( Q \),即 \( q = q(Q, t) \),则新的拉格朗日量 \( L' \) 是新坐标的函数: \[ L'(\mathbf{Q}, \dot{\mathbf{Q}}, t) = L(\mathbf{q}(\mathbf{Q}, t), \dot{\mathbf{q}}(\mathbf{Q}, \dot{\mathbf{Q}}, t), t),~ \] 根据偏微分的链式法则,拉格朗日方程在此变换下是不变的;[41] \[ \frac{\mathrm{d}}{\mathrm{d} t} \frac{\partial L'}{\partial \dot{Q}_{i}} = \frac{\partial L'}{\partial Q_{i}}.~ \] 这可能简化运动方程。
证明
对于坐标变换 \({\displaystyle Q_{i}=Q_{i}(\mathbf {q} ,t)}\),我们有 \[{\displaystyle d{Q_{i}}=\sum _{k}{\frac {\partial Q_{i}}{\partial q_{k}}}d{q_{k}}+{\frac {\partial Q_{k}}{\partial t}}dt,}~\] 这意味着 \[{\displaystyle {\dot {Q_{i}}}=\sum _{k}{\frac {\partial Q_{i}}{\partial q_{k}}}(\mathbf {q} ,t)\,{\dot {q}}_{k}+{\frac {\partial Q_{k}}{\partial t}}(\mathbf {q} ,t)}~,\] 这意味着 \[{\displaystyle {\frac {\partial {\dot {Q_{i}}}}{\partial {\dot {q}}_{k}}}={\frac {\partial Q_{i}}{\partial q_{k}}}}~.\] 还可以得出: \[{\displaystyle {\frac {\partial {\dot {Q_{i}}}}{\partial q_{j}}}=\sum _{k}{\frac {\partial ^{2}Q_{i}}{\partial q_{j}\partial q_{k}}}(\mathbf {q} ,t)\,{\dot {q}}_{k}+{\frac {\partial ^{2}Q_{k}}{\partial q_{j}\partial t}}(\mathbf {q} ,t)}~\] 同样地: \[{\displaystyle {\frac {d}{dt}}\left({\frac {\partial {Q_{i}}}{\partial q_{j}}}\right)=\sum _{k}{\frac {\partial ^{2}Q_{i}}{\partial q_{k}\partial q_{j}}}(\mathbf {q} ,t)\,{\dot {q}}_{k}+{\frac {\partial ^{2}Q_{k}}{\partial t\partial q_{j}}}(\mathbf {q} ,t)}~\]。 这意味着 \[ \frac{d}{dt}\left(\frac{\partial Q_{i}}{\partial q_{k}}\right)=\frac{\partial \dot{Q}_{i}}{\partial q_{k}}.~ \] 这两个推导的关系可以用于证明。
从初始的广义坐标的欧拉-拉格朗日方程出发,我们有: \[ \frac{\partial L}{\partial \dot{q}} - \frac{\partial L}{\partial q} = 0~ \] \[ \sum_{k}\left(\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{Q}_{k}}\right) - \frac{\partial L}{\partial Q_{k}} \frac{\partial Q_{k}}{\partial q} - \frac{\partial L}{\partial \dot{Q}_{k}} \frac{\partial \dot{Q}_{k}}{\partial q}\right) = 0~ \] \[ \sum_{k}\left(\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{Q}_{k}}\right)\frac{\partial \dot{Q}_{k}}{\partial \dot{q}} + \frac{\partial L}{\partial \dot{Q}_{k}} \frac{d}{dt}\left(\frac{\partial \dot{Q}_{k}}{\partial \dot{q}}\right) - \frac{\partial L}{\partial Q_{k}} \frac{\partial \dot{Q}_{k}}{\partial \dot{q}} - \frac{\partial L}{\partial \dot{Q}_{k}} \frac{d}{dt}\left(\frac{\partial Q_{k}}{\partial q}\right)\right) = 0~ \] \[ \sum_{k}\left(\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{Q}_{k}}\right) - \frac{\partial L}{\partial \dot{Q}_{k}}\right) \frac{\partial Q_{k}}{\partial q} = 0~ \] 由于从 \( q \rightarrow Q \) 的变换是可逆的,因此欧拉-拉格朗日方程的形式是不变的,即: \[ \frac{d}{dt}\frac{\partial L}{\partial \dot{Q}_{i}} - \frac{\partial L}{\partial Q_{i}} = 0.~ \]
循环坐标与守恒动量
拉格朗日的一个重要属性是,守恒量可以很容易地从中读出。与坐标 \( q_i \) '正则共轭' 的广义动量定义为 \[ p_{i} = \frac{\partial L}{\partial \dot{q}_{i}}.~ \] 如果拉格朗日量 \( L \) 不依赖于某个坐标 \( q_i \),那么根据欧拉-拉格朗日方程可以立即得出 \[ \dot{p}_{i} = \frac{d}{dt} \frac{\partial L}{\partial \dot{q}_{i}} = \frac{\partial L}{\partial q_{i}} = 0~ \] 并且积分显示对应的广义动量等于一个常数,这是一个守恒量。这是诺特定理的一个特例。这种坐标称为 “循环” 或 “可忽略” 的坐标。
例如,一个系统可能具有拉格朗日量 \[ L(r, \theta, \dot{s}, \dot{z}, \dot{r}, \dot{\theta}, \dot{\phi}, t),~ \] 其中 \( r \) 和 \( z \) 是沿直线的长度,\( s \) 是沿某条曲线的弧长,而 \( \theta \) 和 \( \phi \) 是角度。注意,尽管 \( z \)、\( s \) 和 \( \phi \) 的速度不为零,但它们在拉格朗日量中是缺失的。那么动量 \[ p_{z} = \frac{\partial L}{\partial \dot{z}}, \quad p_{s} = \frac{\partial L}{\partial \dot{s}}, \quad p_{\phi} = \frac{\partial L}{\partial \dot{\phi}},~ \] 都是守恒量。每个广义动量的单位和性质将依赖于相应的坐标;在这种情况下,\( p_z \) 是沿 \( z \) 方向的平动动量,\( p_s \) 也是沿测量曲线 \( s \) 的平动动量,而 \( p_{\phi} \) 是在测量角度 \( \phi \) 的平面中的角动量。无论系统的运动多么复杂,所有坐标和速度都将以一种方式变化,使得这些动量是守恒的。
能量
给定一个拉格朗日量 \( L \),相应机械系统的哈密顿量定义为 \[ H = \left(\sum_{i=1}^{n} \dot{q}_{i} \frac{\partial L}{\partial \dot{q}_{i}}\right) - L.~ \] 如果广义坐标是自然坐标,即在表达位置向量时没有显式的时间依赖性:\(\mathbf{r} = \mathbf{r}(q_{1}, \cdots, q_{n}),\) 那么这个量将等于能量。从: \[ T = \frac{m}{2} v^{2} = \frac{m}{2} \sum_{i,j} \left(\frac{\partial \mathbf{r}}{\partial q_{i}} \dot{q}_{i}\right) \cdot \left(\frac{\partial \mathbf{r}}{\partial q_{j}} \dot{q}_{j}\right) = \frac{m}{2} \sum_{i,j} a_{ij} \dot{q}_{i} \dot{q}_{j}~ \] 可以得出: \[ \sum_{k=1}^{n} \dot{q}_{k} \frac{\partial L}{\partial \dot{q}_{k}} = \sum_{k=1}^{n} \dot{q}_{k} \frac{\partial T}{\partial \dot{q}_{k}} = \frac{m}{2} \left(2\sum_{i,j} a_{ij} \dot{q}_{i} \dot{q}_{j}\right) = 2T.~ \] 因此: \[ H = \left(\sum_{i=1}^{n} \dot{q}_{i} \frac{\partial L}{\partial \dot{q}_{i}}\right) - L = 2T - (T - V) = T + V = E,~ \] 其中 \[ a_{ij} = \frac{\partial \mathbf{r}}{\partial q_{i}} \cdot \frac{\partial \mathbf{r}}{\partial q_{j}}~ \] 是一个对称矩阵,为推导而定义。
坐标变换下的不变性
在每个时刻 \( t \),能量在配置空间坐标变化 \( q \rightarrow Q \) 下是不变的,即(使用自然坐标) \[ E(\mathbf{q}, \dot{\mathbf{q}}, t) = E(\mathbf{Q}, \dot{\mathbf{Q}}, t).~ \] 除了这一结果,下面的证明表明,在这种坐标变化下,导数 \(\partial L/\partial \dot{q}_{i}\) 作为线性形式的系数发生变化。
证明
对于坐标变换 \( Q = F(q) \),我们有 \[ d\mathbf{Q} = F_{*}(\mathbf{q}) d\mathbf{q},~ \] 其中 \( F_{*}(\mathbf{q}) \) 是从向量空间 \[ \left\{\sum_{i=1}^{n} \dot{q}_{i} \cdot \left(\left.\frac{\partial}{\partial q_{i}}\right|_{\mathbf{q}}\right) \bigg| \dot{q}_{i} \in \mathbb{R} \right\}~ \] 到向量空间 \[ \left\{\sum_{i=1}^{n} \dot{Q}_{i} \cdot \left(\left.\frac{\partial}{\partial Q_{i}}\right|_{F(\mathbf{q})}\right) \bigg| \dot{Q}_{i} \in \mathbb{R} \right\}~ \] 的切映射,并且 \[ F_{*}(\mathbf{q}) = \left(\left.\frac{\partial F_{i}}{\partial q_{j}}\right|_{\mathbf{q}}\right)_{i,j=1}^{n}~ \] 是雅可比矩阵。在坐标 \( \dot{q}_{i} \) 和 \( \dot{Q}_{i} \) 中,之前关于 \( d\mathbf{Q} \) 的公式有形式 \(\dot{\mathbf{Q}} = F_{*}(\mathbf{q}) \dot{\mathbf{q}}\).经过涉及乘积法则的微分, \[{\displaystyle d{\dot {\mathbf {Q}}} = G(\mathbf {q}, {\dot {\mathbf {q}}}) d\mathbf {q} + F_{*}(\mathbf {q}) d{\dot {\mathbf {q}}},} ~\] 其中
在向量表示中,
守恒
在拉格朗日力学中,当且仅当拉格朗日量 \( L \) 不显式依赖于时间时,系统是封闭的。能量守恒定律指出,封闭系统的能量 \( E \) 是一个运动的积分。
更准确地说,设 \( q = q(t) \) 是一个极值轨迹(换句话说,\( q \) 满足欧拉–拉格朗日方程)。沿着这个极值轨迹取拉格朗日量 \( L \) 的总时间导数,并利用欧拉–拉格朗日方程,可以得到: \[ \begin{aligned} \frac{dL}{dt} &= \dot{\mathbf{q}} \frac{\partial L}{\partial \mathbf{q}} + \ddot{\mathbf{q}} \frac{\partial L}{\partial \dot{\mathbf{q}}} + \frac{\partial L}{\partial t} \\ - \frac{\partial L}{\partial t} &= \frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\mathbf{q}}}\right) \dot{\mathbf{q}} + \ddot{\mathbf{q}} \frac{\partial L}{\partial \dot{\mathbf{q}}} - \dot{L} \\ - \frac{\partial L}{\partial t} &= \frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\mathbf{q}}} \dot{\mathbf{q}} - L\right) = \frac{dH}{dt} \end{aligned}~ \] 如果拉格朗日量 \( L \) 不显式依赖于时间,则 \( \frac{\partial L}{\partial t} = 0 \),这意味着哈密顿量 \( H \) 随粒子的时间演化不变,实际上是一个运动的积分,这意味着 \[ H(\mathbf{q}(t), \dot{\mathbf{q}}(t), t) = \text{常数}.~ \] 因此,如果选择的坐标是自然坐标,能量就是守恒的。
动能和势能
在所有这些情况下[42],常量 \[ E = T + V~ \] 是系统的总能量。动能和势能在系统演化过程中仍然会变化,但系统的运动使得它们的和,即总能量是恒定的。这是一个有价值的简化,因为能量 \( E \) 是一个积分常数,作为问题的任意常数,并且可能通过这个能量关系从速度积分来求解坐标。
机械相似性
如果势能是坐标的齐次函数并且与时间无关[43],且所有位置矢量都按相同的非零常数 \( \alpha \) 进行缩放,即 \( \mathbf{r}'_k = \alpha \mathbf{r}_k \),那么 \[ V(\alpha \mathbf{r}_1, \alpha \mathbf{r}_2, \ldots, \alpha \mathbf{r}_N) = \alpha^{N} V(\mathbf{r}_1, \mathbf{r}_2, \ldots, \mathbf{r}_N)~ \] 同时如果时间按因子 \( \beta \) 缩放,即 \( t' = \beta t \),那么速度 \( v_k \) 将按 \( \alpha/\beta \) 缩放,动能 \( T \) 将按 \( (\alpha/\beta)^2 \) 缩放。如果整个拉格朗日量也按相同因子缩放,满足 \[ \frac{\alpha^{2}}{\beta^{2}} = \alpha^{N} \quad \Rightarrow \quad \beta = \alpha^{1 - \frac{N}{2}}.~ \] 由于长度和时间被缩放,系统中粒子的轨迹遵循几何相似的路径,只是在大小上有所不同。原始轨迹中在时间 \( t \) 内行进的长度 \( l \) 对应于新轨迹中在时间 \( t' \) 内行进的新长度 \( l' \),由以下比率给出: \[ \frac{t'}{t} = \left( \frac{l'}{l} \right)^{1 - \frac{N}{2}}.~ \]
相互作用粒子
对于给定系统,如果两个子系统 \( A \) 和 \( B \) 之间不相互作用,则整体系统的拉格朗日量 \( L \) 是子系统的拉格朗日量 \( L_A \) 和 \( L_B \) 的和:[38] \[ L = L_{A} + L_{B}.~ \] 如果它们确实相互作用,则无法这样处理。在某些情况下,可以将系统的拉格朗日量 \( L \) 分解为不相互作用的拉格朗日量之和,加上包含相互作用信息的拉格朗日量 \( L_{AB} \): \[ L = L_{A} + L_{B} + L_{AB}.~ \] 这可以通过将不相互作用的拉格朗日量视为动能,而相互作用拉格朗日量视为系统的总势能来进行物理动机化。此外,在相互作用可忽略的极限情况下,\( L_{AB} \) 会趋近于零,简化为上述不相互作用的情况。
扩展到两个以上不相互作用的子系统是直接的——整体拉格朗日量是每个子系统单独拉格朗日量的和。如果存在相互作用,则可以添加相互作用拉格朗日量。
奇异拉格朗日量的后果
根据欧拉–拉格朗日方程,可以得出以下结论: \[ \frac{d}{dt} \frac{\partial L}{\partial \dot{q}_{i}} - \frac{\partial L}{\partial q_{i}} = 0~ \] \[ \frac{\partial^{2} L}{\partial q_{j} \partial \dot{q}_{i}} \frac{dq_{j}}{dt} + \frac{\partial^{2} L}{\partial \dot{q}_{j} \partial \dot{q}_{i}} \frac{d\dot{q}_{j}}{dt} + \frac{\partial L}{\partial t} - \frac{\partial L}{\partial q_{i}} = 0~ \] \[ \sum_{j} W_{ij}(q, \dot{q}, t) \ddot{q}_{j} = \frac{\partial L}{\partial q_{i}} - \frac{\partial L}{\partial t} - \sum_{j} \frac{\partial^{2} L}{\partial \dot{q}_{i} \partial q_{j}} \dot{q}_{j},~ \] 其中矩阵定义为 \(W_{ij} = \frac{\partial^{2} L}{\partial \dot{q}_{i} \partial \dot{q}_{j}}.\) 如果矩阵 \( W \) 是非奇异的,上述方程可以被求解,以将 \( \ddot{q} \) 表示为 \( (\dot{q}, q, t) \) 的函数。如果矩阵是不可逆的,则无法将所有的 \( \ddot{q} \) 表示为 \( (\dot{q}, q, t) \) 的函数,并且哈密顿运动方程也不会呈现标准形式。[44]
4. 示例
以下示例将拉格朗日的第二类方程应用于机械问题。
保守力
一个质量为 \( m \) 的粒子在一个源自标量势 \( V \) 的梯度 \( \nabla \) 影响下运动, \[ \mathbf{F} = -\nabla V(\mathbf{r}).~ \] 如果有多个粒子,根据上述结果,总动能是所有粒子动能的总和,势能是所有坐标的函数。
笛卡尔坐标
粒子的拉格朗日量可以写成 \[ L(x, y, z, \dot{x}, \dot{y}, \dot{z}) = \frac{1}{2} m (\dot{x}^2 + \dot{y}^2 + \dot{z}^2) - V(x, y, z).~ \] 粒子的运动方程通过应用欧拉–拉格朗日方程找到,对于 \( x \) 坐标: \[ \frac{d}{dt} \left( \frac{\partial L}{\partial \dot{x}} \right) = \frac{\partial L}{\partial x},~ \] 其导数为 \[ \frac{\partial L}{\partial x} = -\frac{\partial V}{\partial x}, \quad \frac{\partial L}{\partial \dot{x}} = m \dot{x}, \quad \frac{d}{dt} \left( \frac{\partial L}{\partial \dot{x}} \right) = m \ddot{x},~ \] 因此, \[ m \ddot{x} = -\frac{\partial V}{\partial x},~ \] 对于 \( y \) 和 \( z \) 坐标也类似。将这些方程集合成向量形式,我们得到 \[ m \ddot{\mathbf{r}} = -\nabla V,~ \] 这就是受保守力作用的粒子的牛顿第二运动定律。
二维和三维的极坐标
使用在物理中常用的球坐标 \((r, \theta, \phi)\)(ISO 80000-2:2019 规范),其中 \(r\) 是到原点的径向距离,\(\theta\) 是极角(也称为余纬度、天顶角、法线角或倾角),\(\phi\) 是方位角,中心势的拉格朗日量为 \[ L = \frac{m}{2} \left( \dot{r}^{2} + r^{2} \dot{\theta}^{2} + r^{2} \sin^{2} \theta \, \dot{\phi}^{2} \right) - V(r).~ \] 因此,在球坐标中,欧拉–拉格朗日方程为 \[ m \ddot{r} - mr(\dot{\theta}^{2} + \sin^{2} \theta \, \dot{\phi}^{2}) + \frac{\partial V}{\partial r} = 0,~ \] \[ \frac{d}{dt} (mr^{2} \dot{\theta}) - mr^{2} \sin \theta \cos \theta \, \dot{\phi}^{2} = 0,~ \] \[ \frac{d}{dt} (mr^{2} \sin^{2} \theta \, \dot{\phi}) = 0.~ \] \(\phi\) 坐标是循环坐标,因为它在拉格朗日量中没有出现,因此系统中守恒的动量是角动量 \[ p_{\phi} = \frac{\partial L}{\partial \dot{\phi}} = mr^{2} \sin^{2} \theta \, \dot{\phi},~ \] 其中 \(r\)、\(\theta\) 和 \(d\phi/dt\) 都可以随时间变化,但只有在 \(p_{\phi}\) 保持不变的情况下。
通过将 \(\theta\) 固定为常数值 \(\pi/2\),可以恢复二维极坐标中的拉格朗日量。
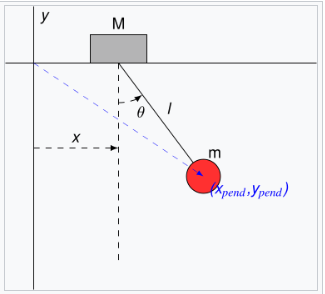
在可移动支撑上的摆
考虑一个质量为 \( m \)、长度为 \( \ell \) 的摆,它被固定在一个质量为 \( M \) 的支撑上,支撑可以沿 \( x \) 方向移动。设 \( x \) 为支撑沿线的坐标,摆的位置由与竖直方向的夹角 \( \theta \) 表示。摆锤的坐标和速度分量为: \[ \begin{array}{rll} x_{\mathrm{pend}} &= x + \ell \sin \theta & \quad \Rightarrow \quad \dot{x}_{\mathrm{pend}} = \dot{x} + \ell \dot{\theta} \cos \theta \\ y_{\mathrm{pend}} &= -\ell \cos \theta & \quad \Rightarrow \quad \dot{y}_{\mathrm{pend}} = \ell \dot{\theta} \sin \theta. \end{array}~ \] 广义坐标可以取为 \( x \) 和 \( \theta \)。系统的动能为: \[ T = \frac{1}{2} M \dot{x}^2 + \frac{1}{2} m \left( \dot{x}_{\mathrm{pend}}^2 + \dot{y}_{\mathrm{pend}}^2 \right),~ \] 而势能为: \[ V = mg y_{\mathrm{pend}}.~ \] 因此,拉格朗日量为:
双体中心力问题
两个质量为 \( m_1 \) 和 \( m_2 \) 的物体,其位置矢量分别为 \( \mathbf{r}_1 \) 和 \( \mathbf{r}_2 \),由于吸引中心势能 \( V \) 而互相绕转。我们可以直接用位置坐标写出拉格朗日量,但将双体问题转化为单体问题是一种常用的程序。引入雅可比坐标;物体之间的距离 \( \mathbf{r} = \mathbf{r}_2 - \mathbf{r}_1 \) 和质心的位置 \( \mathbf{R} =(m_1 \mathbf{r}_1 + m_2 \mathbf{r}_2)/(m_1 + m_2) \)。拉格朗日量则为: \[ L = \underbrace{\frac{1}{2} M \dot{\mathbf{R}}^2}_{L_{\text{cm}}} + \underbrace{\frac{1}{2} \mu \dot{\mathbf{r}}^2 - V(|\mathbf{r}|)}_{L_{\text{rel}}}~ \] 其中 \( M = m_1 + m_2 \) 是总质量,\( \mu = m_1 m_2/(m_1 + m_2) \) 是约化质量,\( V \) 是径向力的势能,仅依赖于分离距离的大小 \( |\mathbf{r}| = |\mathbf{r}_2 - \mathbf{r}_1| \)。拉格朗日量分为质心项 \( L_{\text{cm}} \) 和相对运动项 \( L_{\text{rel}} \)。
对 \( \mathbf{R} \) 的欧拉–拉格朗日方程为: \[ M {\ddot {\mathbf{R}}} = 0,~ \] 这表明质心以恒定速度沿直线运动。
由于相对运动仅依赖于分离的大小,因此理想的做法是使用极坐标 \( (r, \theta) \) 并取 \( r = |\mathbf{r}| \): \[ L_{\text{rel}} = \frac{1}{2} \mu \left( {\dot{r}}^{2} + r^{2} {\dot{\theta}}^{2} \right) - V(r),~ \] 因此 \( \theta \) 是一个循环坐标,对应的守恒(角)动量为: \[ p_{\theta} = \frac{\partial L_{\text{rel}}}{\partial {\dot{\theta}}} = \mu r^{2} {\dot{\theta}} = \ell.~ \] 径向坐标 \( r \) 和角速度 \( d\theta/dt \) 可以随时间变化,但仅以使得 \( \ell \) 保持常数的方式变化。对于 \( r \) 的拉格朗日方程为: \[ \mu r {\dot{\theta}}^{2} - \frac{dV}{dr} = \mu {\ddot{r}}.~ \] 这个方程与在共同旋转参考框架中使用牛顿定律获得的径向方程是相同的,即一个与约化质量一起旋转的框架,使其看起来是静止的。通过消去角速度 \( d\theta/dt \) 这个径向方程,可以得到: \[ \mu {\ddot {r}} = -\frac{dV}{dr} + \frac{\ell^2}{\mu r^3}.~ \] 这是一个一维问题的运动方程,其中质量为 \( \mu \) 的粒子受到向内的中心力 \( -dV/dr\) 和一个向外的第二个力,这在此上下文中称为(拉格朗日)离心力: \[ F_{\mathrm{cf}} = \mu r \dot{\theta}^2 = \frac{\ell^2}{\mu r^3}.~ \] 当然,如果完全局限于一维表述,\( \ell \) 仅作为施加的外向力的参数出现,而它作为角动量的解释则依赖于更一般的二维问题,这个问题是从一维问题衍生而来的。
如果在共同旋转的框架中使用牛顿力学得到这个方程,那么它作为该框架中由于框架本身旋转而产生的离心力的解释是显而易见的。如果直接通过使用广义坐标 \( (r, \theta) \) 并简单地遵循拉格朗日表述而不考虑框架,离心力的解释则是它是使用极坐标的自然结果。正如希尔德布兰所说:[48]
“由于这些量不是实际的物理力,因此通常被称为惯性力。它们的存在与否并不取决于具体的问题,而是取决于所选择的坐标系统。” 特别地,如果选择笛卡尔坐标,离心力就会消失,公式中只涉及中心力本身,这提供了曲线运动所需的向心力。
这种观点,即虚拟力源于坐标的选择,通常由拉格朗日方法的使用者表达。这种观点在拉格朗日方法中自然而然地出现,因为参考系(可能是在无意识中)是通过选择坐标来确定的。例如,可以参考[49]比较惯性框架和非惯性框架中的拉格朗日量。还可以参考关于 “总” 拉格朗日量和 “更新” 拉格朗日量表述的讨论。[50]不幸的是,这种 “惯性力” 的用法与牛顿对惯性力的定义相矛盾。在牛顿的观点中,惯性力源于观察框架的加速度(即它不是一个惯性参考框架),而不是坐标系的选择。为了保持清晰,最好将拉格朗日惯性力称为广义惯性力,以将其与牛顿的矢量惯性力区分开来。也就是说,应避免跟随希尔德布兰的说法(第 155 页)“我们总是处理广义力、速度、加速度和动量。为简洁起见,形容词‘广义的’将被频繁省略。”
众所周知,一个系统的拉格朗日量不是唯一的。在拉格朗日形式主义中,可以通过存在替代拉格朗日量来识别牛顿的虚构力,在这些替代拉格朗日量中,虚构力消失,这有时是通过利用系统的对称性找到的。[51]
5. 扩展以包括非保守力
耗散力
耗散(即非保守系统)也可以通过某种程度的自由度加倍来处理,形成一个有效的拉格朗日量。[52][53][54][55]
在更一般的表述中,力可以是保守的和粘性的。如果能找到适当的转换,Rayleigh 建议使用以下形式的耗散函数 D:[56] \[ D = \frac{1}{2} \sum_{j=1}^{m} \sum_{k=1}^{m} C_{jk} \dot{q}_{j} \dot{q}_{k},~ \] 其中 \( C_{jk} \) 是与物理系统中的阻尼系数相关的常数,但不一定等于它们。如果 D 以这种方式定义,则有[56]: \[ Q_{j} = -\frac{\partial V}{\partial q_{j}} - \frac{\partial D}{\partial \dot{q}_{j}} ~\] 以及 \[ \frac{d}{dt} \left( \frac{\partial L}{\partial \dot{q}_{j}} \right) - \frac{\partial L}{\partial q_{j}} + \frac{\partial D}{\partial \dot{q}_{j}} = 0.~ \]
电磁学
测试粒子是指质量和电荷被假设得非常小,以至于对外部系统的影响微不足道的粒子。它通常是一个假设的简化点粒子,除了质量和电荷外没有其他属性。真实的粒子,如电子和上夸克,更为复杂,其拉格朗日量中包含额外的项。这些场不仅可以形成非保守势能,这些势能也可以依赖于速度。
带电粒子的拉格朗日量是与电磁场相互作用的典型例子,它包含速度依赖的势能。电场 \( \mathbf{E} = \mathbf{E}(r, t) \) 和磁场 \( \mathbf{B} = \mathbf{B}(r, t) \) 由电势标量 \( \phi = \phi(r, t) \) 和磁矢势 \( \mathbf{A} = \mathbf{A}(r, t) \) 定义如下: \[ \mathbf{E} = -\nabla \phi - \frac{\partial \mathbf{A}}{\partial t}, \quad \mathbf{B} = \nabla \times \mathbf{A}.~ \] 带电质量测试粒子在电磁场中的拉格朗日量 \[ L={\tfrac {1}{2}}m{\dot {\mathbf {r}}}^{2}+q\,{\dot {\mathbf {r}}}\cdot \mathbf {A} -q\phi,~ \] 称为最小耦合。这是一个很好的例子,说明常见的经验法则(拉格朗日量是动能减去势能)并不总是正确。结合欧拉-拉格朗日方程,它产生了洛伦兹力定律: \[ m{\ddot {\mathbf {r}}}=q\mathbf {E} +q{\dot {\mathbf {r}}}\times \mathbf {B}.~ \] 在规范变换下: \[ \mathbf {A} \rightarrow \mathbf {A} +{\boldsymbol {\nabla }}f,\quad \phi \rightarrow \phi -{\dot {f}},~ \] 其中 \( f(r,t) \) 是空间和时间的任意标量函数,上述拉格朗日量变换为: \[ L\rightarrow L+q\left({\dot {\mathbf {r}}}\cdot {\boldsymbol {\nabla }}+{\frac {\partial }{\partial t}}\right)f=L+q{\frac {df}{dt}},~ \] 这仍然产生相同的洛伦兹力定律。 注意,动量(与位置 \( r \) 共轭)是动动量加上来自 \( A \) 场的贡献(称为势动量): \[ \mathbf {p} =\frac {\partial L}{\partial {\dot {\mathbf {r}}}}=m{\dot {\mathbf {r}}}+q\mathbf {A} .~ \] 这个关系在量子力学和量子场论的最小耦合规则中也得到了应用。从这个表达式中,我们可以看到,规范动量 \( p \) 不是规范不变的,因此不是一个可测量的物理量;然而,如果 \( r \) 是循环坐标(即拉格朗日量不依赖于位置 \( r \)),这在 \( \phi \) 和 \( A \) 场均匀时发生,那么这里给出的规范动量 \( p \) 是守恒动量,而可测量的物理动量 \( mv \) 不是。
6. 其他背景和表述
拉格朗日力学中的思想在物理学的其他领域有着众多应用,并且可以采用变分法中的广义结果。
经典力学的替代表述
经典力学的一种密切相关的表述是哈密顿力学。哈密顿量定义为 \[ H = \sum_{i=1}^{n} \dot{q}_{i} \frac{\partial L}{\partial \dot{q}_{i}} - L~ \] 可以通过对拉格朗日量进行勒让德变换获得,这引入了与原始变量规范共轭的新变量。例如,给定一组广义坐标,规范共轭的变量是广义动量。这使变量的数量翻倍,但使得微分方程成为一阶方程。哈密顿量在量子力学中是一个特别普遍的量(参见哈密顿量(量子力学))。
拉塞尔力学是一种拉格朗日力学和哈密顿力学的混合表述,虽然在实践中不常用,但对于循环坐标是一种有效的表述。
动量空间表述
欧拉–拉格朗日方程也可以用广义动量而非广义坐标来表述。对广义坐标拉格朗日量 \( L(q, \dot{q}, t) \) 进行勒让德变换,可以得到广义动量拉格朗日量 \( L'(p, \dot{p}, t) \),同时也可以得到以广义动量为变量的欧拉–拉格朗日方程。这两个拉格朗日量包含相同的信息,任一者都可以用于求解系统的运动。在实践中,广义坐标比广义动量更方便使用和解释。
广义坐标的高阶导数
在数学上没有理由仅限于广义坐标的导数为一阶。可以推导出包含高阶导数的拉格朗日量的修正欧拉–拉格朗日方程,详见欧拉–拉格朗日方程。然而,从物理角度来看,包含高于一阶的时间导数存在障碍,这由奥斯特罗格拉德斯基对非退化高阶导数拉格朗日量的规范形式的构造所暗示,详见奥斯特罗格拉德斯基不稳定性。
光学
拉格朗日力学可以应用于几何光学,通过将变分原理应用于介质中的光线,并求解欧拉–拉格朗日方程,得到光线传播路径的方程。
相对论的表述
拉格朗日力学可以在狭义相对论和广义相对论中进行表述。尽管拉格朗日力学的一些特征在相对论理论中得以保留,但在其他方面会迅速出现困难。特别是,欧拉-拉格朗日方程保持相同形式,循环坐标与守恒动量之间的联系仍然适用,然而拉格朗日量必须进行修正,并不只是粒子的动能减去势能。此外,以显式协变的方式处理多粒子系统并不简单,但如果单独选择一个特定的参考框架,可能会有所帮助。
量子力学
在量子力学中,作用量与量子相位通过普朗克常数相关联,驻留作用原理可以通过波函数的构造干涉来理解。
1948 年,费曼发现了路径积分表述,将最小作用原理扩展到电子和光子的量子力学中。在这种表述中,粒子沿着从初始状态到最终状态的每条可能路径运动;特定最终状态的概率是通过对所有可能轨迹进行求和获得的。在经典范围内,路径积分表述干净地重现了哈密尔顿原理,以及光学中的费马原理。
经典场论
在拉格朗日力学中,广义坐标构成一组离散变量,用以定义系统的状态。在经典场论中,物理系统不是一组离散粒子,而是定义在三维空间区域上的连续场ϕ(r, t)。与该场相关联的是一个拉格朗日密度 \[ \mathcal{L}(\phi, \nabla \phi, \dot{\phi}, \mathbf{r}, t)~ \] 它是基于场及其在位置 r 和时间 t 的空间和时间导数定义的。类似于粒子的情况,对于非相对论应用,拉格朗日密度也可以看作是场的动能密度减去其势能密度(这在一般情况下并不成立,拉格朗日密度需要 “反向工程”)。然后,拉格朗日是拉格朗日密度在三维空间上的体积积分: \[ L(t) = \int \mathcal{L} \, \mathrm{d}^{3}\mathbf{r}~ \] 其中,d³r 是三维微分体积元素。拉格朗日是时间的函数,因为拉格朗日密度通过场隐含地依赖于空间,并且可能具有显式的空间依赖性,但在积分中这些依赖被去除,只留下时间作为拉格朗日的变量。
诺特定理
作用原理和拉格朗日形式与诺特定理密切相关,该定理将物理守恒量与物理系统的连续对称性联系起来。
如果拉格朗日对某一对称性不变,则由此产生的运动方程也将在该对称性下保持不变。这一特性在证明理论与特殊相对论或广义相对论一致性方面非常有帮助。
7. 另见
- 规范坐标
- 变分法的基本引理
- 泛函导数
- 广义坐标
- 哈密顿力学
- 哈密顿光学
- 拉格朗日力学的逆问题,即在给定运动方程的情况下寻找系统的拉格朗日。
- 流场的拉格朗日和欧拉描述
- 拉格朗日点
- 拉格朗日系统
- 非自治力学
- 普拉托问题
- 受限三体问题
8. 脚注
- 有时在这种情况下,变分导数表示并定义为 \[ \frac{\delta}{\delta \mathbf{r}_k} \equiv \frac{\partial}{\partial \mathbf{r}_k} - \frac{d}{dt} \frac{\partial}{\partial \dot{\mathbf{r}}_k}~ \] 在本文中,仅使用偏导数和全导数。
- 这里假设虚位移是可逆的,但对于某些系统,可能存在违反这一原则的不可逆虚位移,参见乌德瓦迪亚–卡拉巴方程。
- 换句话说 \[ \mathbf {C} _{k}\cdot \delta \mathbf {r} _{k}=0~ \] 对于受约束力作用的粒子 \(k\),但 \[ C_{k\,x}\delta x_{k}\neq 0,\quad C_{k\,y}\delta y_{k}\neq 0,\quad C_{k\,z}\delta z_{k}\neq 0~ \] 因为约束方程作用于 \(rk\) 坐标。
- 拉格朗日量也可以明确地为旋转参考系写出。参见帕德马纳班,2000。
9. 注释
- 弗雷泽,克雷格。《拉格朗日在力学原理和方法上的早期贡献》。精确科学史档案,第 28 卷,第 3 期,1983 年,第 197–241 页。JSTOR,http://www.jstor.org/stable/41133689。访问日期:2023 年 11 月 3 日。
- Hand & Finch 1998,第 23 页
- Hand & Finch 1998,第 18–20 页
- Hand & Finch 1998,第 46、51 页
- 巴尔,菲利普。(2019 年 9 月 13 日)。《先教能量再教力》。物理学,第 100 页。doi:10.1103/PhysRevPhysEducRes.15.020126。检索日期:2024 年 9 月 27 日。
- 塔图姆,J. B.《拉格朗日力学》(PDF)。www.astro.uvic.ca。检索日期:2024 年 9 月 27 日。
- 帕森斯,保罗;迪克森,盖尔。(2016)。《你真正需要了解的 50 个科学概念》。伦敦:Quercus 出版社,第 4–7 页。ISBN 9781784296148。
- Torby 1984,第 270 页
- Torby 1984,第 269 页
- 克雷马斯基尼,克劳迪奥;泰萨罗托,马西莫。(2015 年 6 月 30 日)。《广义相对论中的同步拉格朗日变分原理》。欧洲物理学杂志 Plus,130 卷(6 期):123。doi:10.1140/epjp/i2015-15123-4。ISSN 2190-5444。
- Bersani, A. M., Caressa, P. 《耗散系统的拉格朗日描述:综述》。固体数学与力学,2021;第 26 卷第 6 期:785-803。doi: 10.1177/1081286520971834。
- Hand & Finch 1998, p. 36–40
- Pfeiffer, Friedrich(2008 年),由 Friedrich Pfeiffer 编,《约束系统》,《机械系统动力学》,柏林,海德堡:Springer 出版社,第 85–186 页,doi:10.1007/978-3-540-79436-3_3,ISBN 978-3-540-79436-3,检索日期:2024 年 9 月 23 日。
- Hand & Finch 1998, p. 60–61
- Hand & Finch 1998, p. 19
- Penrose 2007
- Morin, D.(2007 年)。第 6 章:拉格朗日方法。收录于《拉格朗日方法》。https://scholar.harvard.edu/files/david-morin/files/cmchap6.pdf。
- Kay 1988,第 156 页
- Synge & Schild 1949,第 150–152 页
- Foster & Nightingale 1995,第 89 页
- Hand & Finch 1998,第 4 页
- Goldstein 1980,第 16–18 页
- Hand & Finch 1998,第 15 页
- Hand & Finch 1998,第 15 页
- Fetter & Walecka 1980,第 53 页
- Kibble & Berkshire 2004,第 234 页
- Fetter & Walecka 1980,第 56 页
- Hand & Finch 1998,第 17 页
- Hand & Finch 1998,第 15–17 页
- 彭罗斯,R.(2007 年)。《通向实在之路》。Vintage Books 出版社,第 474 页。ISBN 978-0-679-77631-4。
- Goldstein 1980,第 23 页
- Kibble & Berkshire 2004,第 234–235 页
- Hand & Finch 1998,第 51 页
- Hanc, Jozef;Taylor, Edwin F.;Tuleja, Slavomir(2005 年 7 月 1 日)。《一维和二维中的变分力学》。美国物理学杂志,73 卷(7 期):603–610。Bibcode: 2005AmJPh..73..603H。doi: 10.1119/1.1848516。ISSN 0002-9505。
- Hand & Finch 1998,第 44–45 页
- Goldstein 1980
- Fetter & Walecka 1980,第 68–70 页
- Landau & Lifshitz 1976,第 4 页
- Goldstein, Poole & Safko 2002,第 21 页
- Landau & Lifshitz 1976,第 4 页
- Goldstein 1980,第 21 页
- Landau & Lifshitz 1976,第 14 页
- Landau & Lifshitz 1976,第 22 页
- Rothe, Heinz J;Rothe, Klaus D(2010)。《受限哈密顿系统的经典与量子动力学》。世界科学物理讲座笔记,第 81 卷。世界科学出版社,第 7 页。doi:10.1142/7689。ISBN 978-981-4299-64-0。
- Taylor 2005,第 297 页
- Padmanabhan 2000,第 48 页
- Hand & Finch 1998,第 140–141 页
- Hildebrand 1992,第 156 页
- Zak, Zbilut & Meyers 1997,第 202 页
- Shabana 2008,第 118–119 页
- Gannon 2006,第 267 页
- Kosyakov 2007
- Galley 2013
- Birnholtz, Hadar & Kol 2014
- Birnholtz, Hadar & Kol 2013
- Torby 1984,第 271 页
10. 参考文献
- 拉格朗日,J. L.(1811)。《解析力学》。第 1 卷。
- 拉格朗日,J. L.(1815)。《解析力学》。第 2 卷。
- 彭罗斯,罗杰(2007)。《通向实在之路》。Vintage Books 出版社。ISBN 978-0-679-77631-4。
- 朗道,L. D.;利夫席兹,E. M.(1976 年 1 月 15 日)。《力学》(第 3 版)。巴特沃斯·海因曼出版社,第 134 页。ISBN 9780750628969。
- 朗道,列夫;利夫席兹,叶夫根尼(1975)。《经典场论》。Elsevier 出版社。ISBN 978-0-7506-2768-9。
- 汉德,L. N.;芬奇,J. D.(1998)。《解析力学》(第 2 版)。剑桥大学出版
- 萨勒滕,E. J.;何塞,J. V.(1998)。《经典动力学:一种现代方法》。剑桥大学出版社。ISBN 9780521636360。
- 基布尔,T. W. B.;伯克希尔,F. H.(2004)。《经典力学》(第 5 版)。帝国理工学院出版社,第 236 页。ISBN 9781860944352。
- 戈德斯坦,赫伯特(1980)。《经典力学》(第 2 版)。加利福尼亚州旧金山:艾迪生·韦斯利出版社。ISBN 0201029189。
- 戈德斯坦,赫伯特;普尔,查尔斯 P. Jr.;萨夫科,约翰 L.(2002)。《经典力学》(第 3 版)。加利福尼亚州旧金山:艾迪生·韦斯利出版社。ISBN 0-201-65702-3。
- 兰乔斯,科尔内留斯(1986)。《附加条件:拉格朗日 λ-方法》,《力学的变分原理》(1970 年多伦多大学第 4 版重印)。Courier Dover 出版社,第 43 页。ISBN 0-486-65067-7。
- 费特,A. L.;瓦莱卡,J. D.(1980)。《粒子与连续体的理论力学》。Dover 出版社,第 53–57 页。ISBN 978-0-486-43261-8。
- 《最小作用量原理》,R. 费曼
- 德沃夏克,R.;弗莱斯泰特,弗洛里安(2005)。《第一类拉格朗日方程》。行星系统中的混沌与稳定性。Birkhäuser 出版社,第 24 页。ISBN 3-540-28208-4。
- 哈肯,H(2006)。《信息与自组织》(第 3 版)。Springer 出版社,第 61 页。ISBN 3-540-33021-6。
- 亨利·扎茨基斯(1960)。《第二类拉格朗日方程》。载于 DH 曼泽尔(编)。《物理学基础公式》,第 1 卷(第 2 版)。Courier Dover 出版社,第 160 页。ISBN 0-486-60595-7。
- 希尔德布兰德,弗朗西斯·贝格诺(1992)。《应用数学方法》(1965 年 Prentice-Hall 第 2 版重印)。Courier Dover 出版社,第 156 页。ISBN 0-486-67002-3。
- 扎克,米哈伊尔;兹比鲁特,约瑟夫 P.;迈耶斯,罗纳德 E.(1997)。《从不稳定到智能》。Springer 出版社,第 202 页。ISBN 3-540-63055-4。
- 沙巴纳,艾哈迈德 A.(2008)。《计算连续体力学》。剑桥大学出版社,第 118–119 页。ISBN 978-0-521-88569-0。
- 泰勒,约翰·罗伯特(2005)。《经典力学》。University Science Books 出版社,第 297 页。ISBN 1-891389-22-X。
- 帕德马纳班,塔努(2000)。《旋转框架中的运动》,载于《理论天体物理学:天体物理过程》(第 3 版)。剑桥大学出版社,第 48 页。ISBN 0-521-56632-0。
- 多蒂,诺埃尔·A.(1990)。《拉格朗日相互作用》。艾迪生·韦斯利出版社。ISBN 0-201-41625-5。
- 科斯亚科夫,B. P.(2007)。《粒子与场的经典理论导论》。德国柏林:Springer 出版社。doi:10.1007/978-3-540-40934-2。ISBN 978-3-540-40933-5。
- 加利,查德·R.(2013)。《非保守系统的经典力学》。《物理评论快报》,110 卷(17 期):174301。arXiv:1210.2745。Bibcode:2013PhRvL.110q4301G。doi:10.1103/PhysRevLett.110.174301。PMID 23679733。S2CID 14591873。
- Birnholtz, Ofek;Hadar, Shahar;Kol, Barak(2014)。《作用量层面的辐射反应》。国际现代物理 A 杂志,29 卷(24 期):1450132–1450190。arXiv:1402.2610。Bibcode:2014IJMPA..2950132B。doi:10.1142/S0217751X14501322。S2CID 118541484。
- Birnholtz, Ofek;Hadar, Shahar;Kol, Barak(2013)。《后牛顿辐射和反应理论》。物理评论 D,88 卷(10 期):104037。arXiv:1305.6930。Bibcode:2013PhRvD..88j4037B。doi:10.1103/PhysRevD.88.104037。S2CID 119170985。
- Roger F. Gans(2013)。《工程动力学:从拉格朗日到模拟》。纽约:Springer 出版社。ISBN 978-1-4614-3929-5。
- 甘农,特里(2006)。《超越怪物的月光:连接代数、模形式与物理的桥梁》。剑桥大学出版社,第 267 页。ISBN 0-521-83531-3。
- 托比,布鲁斯(1984)。《能量方法》。工程高级动力学。HRW 机械工程系列。美国:CBS 学院出版社。ISBN 0-03-063366-4。
- 福斯特,J;奈廷格尔,J. D.(1995)。《广义相对论简明教程》(第 2 版)。Springer 出版社。ISBN 0-03-063366-4。
- M. P. 霍布森;G. P. 埃夫斯塔修;A. N. 拉森比(2006)。《广义相对论:物理学家的入门》。剑桥大学出版社,第 79–80 页。ISBN 9780521829519。
- 辛格,J. L.;希尔德,A.(1949)。《张量计算》。Dover 出版社 1978 年第一版。ISBN 978-0-486-63612-2。
- 凯伊,大卫(1988 年 4 月)。《Schaum's 张量计算概要》。麦格劳-希尔专业出版社。ISBN 978-0-07-033484-7。
11. 延伸阅读
- 古普塔,基兰·钱德拉。《粒子和刚体的经典力学》(Wiley 出版社,1988 年)。
- 卡塞尔,凯文(2013)。《变分方法及其在科学与工程中的应用》。剑桥:剑桥大学出版社。ISBN 978-1-107-02258-4。
- 戈德斯坦,赫伯特等。《经典力学》(第 3 版),Pearson 出版社,2002 年。