刚体动力学 （综述）

                     

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章）

图
图 1：波尔顿和瓦特蒸汽机（1784 年）各组成部件的运动可以通过一组运动学和动力学方程来描述。

　　 在动力学的物理科学中，刚体动力学研究在外力作用下互连体系统的运动。假设这些物体是刚体（即在外力作用下不发生变形），这简化了分析，因为系统的配置仅需通过每个物体附加的参考框架的平移和旋转来描述。[1][2]这排除了表现出流体、高弹性和塑性行为的物体。

　　 刚体系统的动力学由运动学定律以及牛顿第二定律（动力学）或其导数形式——拉格朗日力学来描述。这些运动方程的解提供了系统中各个组成部分的位置、运动和加速度的描述，以及整个系统随时间的变化。刚体动力学的公式化和求解是机械系统计算机仿真中的重要工具。

1. 平面刚体动力学

　　 如果一个粒子系统平行于固定平面运动，则称该系统受到平面运动的约束。在这种情况下，刚体系统中 \( N \) 个粒子 \( P_i \)（\( i=1,...,N \)）的牛顿定律（动力学）简化了，因为在 \( k \) 方向上没有运动。可在参考点 \( R \) 处确定合力和力矩，得到： \[ \mathbf{F} = \sum_{i=1}^{N} m_{i} \mathbf{A}_{i}, \quad \mathbf{T} = \sum_{i=1}^{N} (\mathbf{r}_{i} - \mathbf{R}) \times m_{i} \mathbf{A}_{i},~ \] 其中，\( \mathbf{r}_i \) 表示每个粒子的平面轨迹。

　　 刚体运动学给出了粒子 \( P_i \) 的加速度公式，表示为参考点位置 \( \mathbf{R} \) 和加速度 \( \mathbf{A} \)，以及刚体系统的角速度向量 \( \boldsymbol{\omega} \) 和角加速度向量 \( \boldsymbol{\alpha} \)： \[ \mathbf{A}_i = \boldsymbol{\alpha} \times (\mathbf{r}_i - \mathbf{R}) + \boldsymbol{\omega} \times (\boldsymbol{\omega} \times (\mathbf{r}_i - \mathbf{R})) + \mathbf{A}.~ \] 对于约束在平面运动的系统，角速度和角加速度向量沿着垂直于运动平面的 \( k \) 方向，使得此加速度方程简化。在这种情况下，可以通过从参考点 \( R \) 到点 \( r_i \) 的单位向量 \( \mathbf{e}_i \) 以及单位向量 \( \mathbf{t}_i = \mathbf{k} \times \mathbf{e}_i \) 来简化加速度向量，因此有： \[ \mathbf{A}_i = \alpha (\Delta r_i \mathbf{t}_i) - \omega^2 (\Delta r_i \mathbf{e}_i) + \mathbf{A}.~ \] 这给出了系统的合力为： \[ \mathbf{F} = \alpha \sum_{i=1}^{N} m_{i} \left( \Delta r_{i} \mathbf{t}_{i} \right) - \omega^2 \sum_{i=1}^{N} m_{i} \left( \Delta r_{i} \mathbf{e}_{i} \right) + \left( \sum_{i=1}^{N} m_{i} \right) \mathbf{A},~ \] 而力矩为：

\begin{equation} \begin{aligned} \mathbf{T} &= \sum_{i=1}^{N} (m_{i} \Delta r_{i} \mathbf{e}_{i}) \times \left( \alpha (\Delta r_{i} \mathbf{t}_{i}) - \omega^2 (\Delta r_{i} \mathbf{e}_{i}) + \mathbf{A} \right) \\ &= \left( \sum_{i=1}^{N} m_{i} \Delta r_{i}^{2} \right) \alpha \mathbf{k} + \left( \sum_{i=1}^{N} m_{i} \Delta r_{i} \mathbf{e}_{i} \right) \times \mathbf{A}, \end{aligned}~ \end{equation}
其中 \( \mathbf{e}_{i} \times \mathbf{e}_{i} = 0 \) 且 \( \mathbf{e}_{i} \times \mathbf{t}_{i} = \mathbf{k} \)，即垂直于平面的单位向量，适用于所有粒子 \( P_i \)。

　　 使用质心 \( C \) 作为参考点，这些方程在牛顿定律中的简化形式为： \[ \mathbf{F} = M \mathbf{A}, \quad \mathbf{T} = I_C \alpha \mathbf{k},~ \] 其中 \( M \) 为总质量，\( I_C \) 为绕刚体系统运动平面垂直轴且穿过质心的转动惯量。

2. 三维空间中的刚体

方向或姿态描述

　　 已经开发了几种方法来描述三维空间中刚体的方向。这些方法将在以下部分中进行总结。

　　 欧拉角

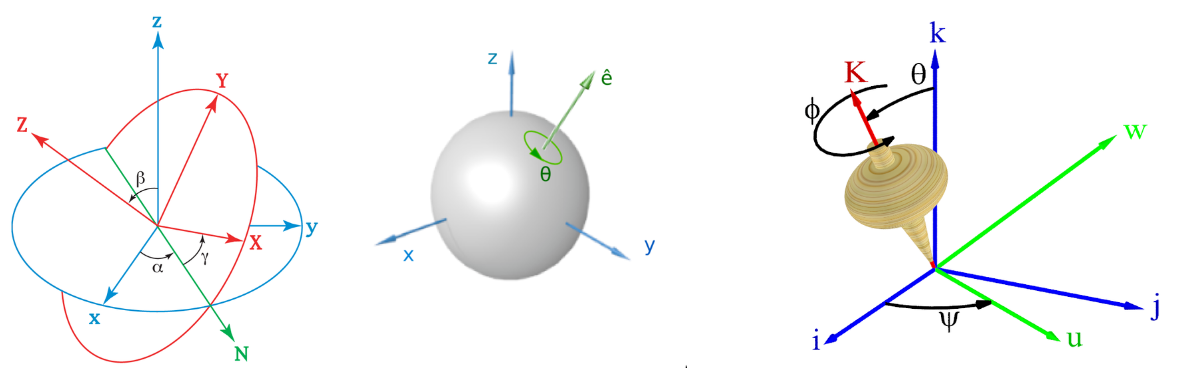
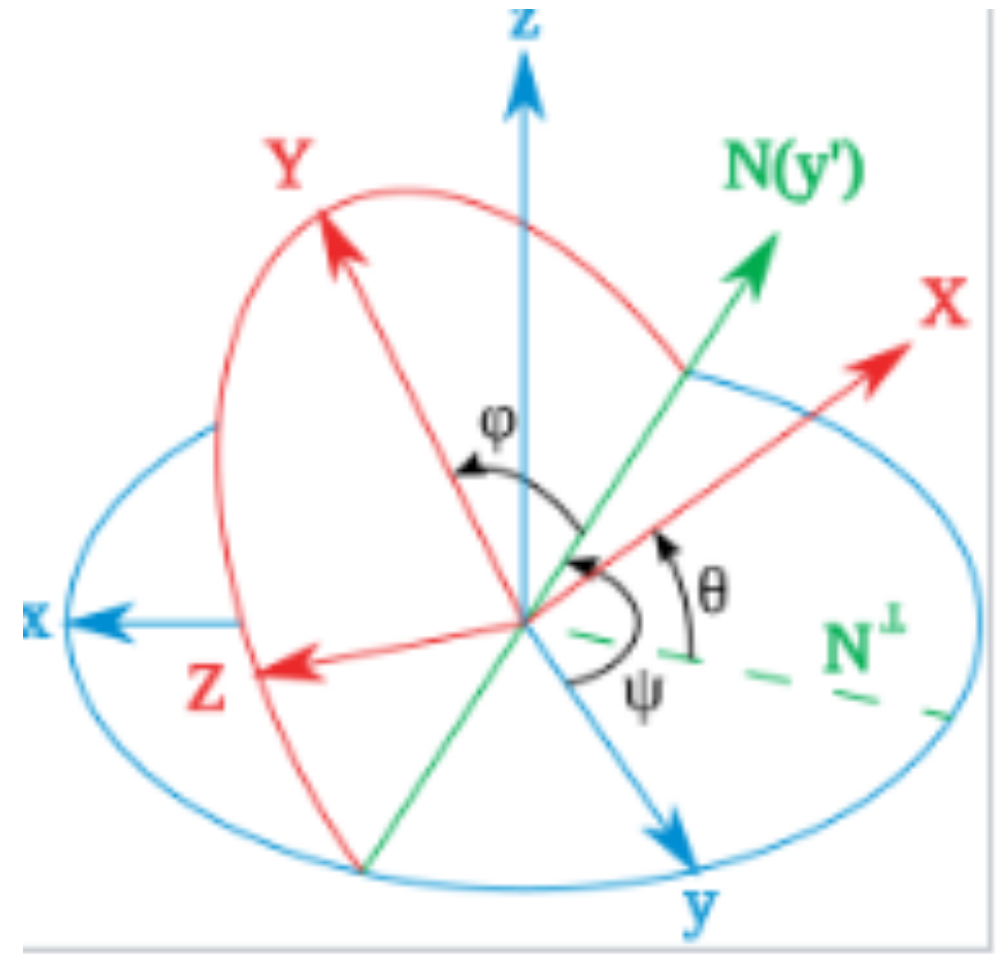
　　 最早用来表示方向的方法归功于莱昂哈德·欧拉。他设想了三个可以相互旋转的参考框架，并意识到通过从一个固定参考框架开始执行三次旋转，可以得到空间中的任何其他参考框架（使用两次旋转来固定垂直轴，再用一次旋转来固定另外两个轴）。这三次旋转的值称为欧拉角。通常，\(\psi\) 用来表示进动，\(\theta\) 表示章动，而 \(\phi\) 表示固有旋转。

图
图 2：欧拉角示意图/球体围绕固定轴的固有旋转/陀螺在欧拉角中的运动

　　 泰特–布莱恩角

　　 这些是三个角，也被称为偏航、俯仰和滚转角，导航角和卡丹角。从数学上来说，它们在十二种可能的欧拉角组合中构成了六种可能性，这种顺序最适合描述如飞机等载具的方向。在航空航天工程中，它们通常被称为欧拉角。

　　 方向向量

　　 欧拉还意识到，两次旋转的组合等效于绕另一个不同固定轴的单次旋转（欧拉旋转定理）。因此，前面三个角的组合必须等同于仅一次旋转，其轴的计算在引入矩阵之前相当复杂。基于这一事实，欧拉引入了一种描述任意旋转的矢量方法，使用旋转轴上的一个矢量，其模等于旋转角度的大小。因此，任何方向都可以通过一个旋转向量（也称为欧拉向量）来表示，该向量从参考框架导向该方向。当用于表示方向时，旋转向量通常称为方向向量或姿态向量。

　　 一种类似的方法称为轴角表示，使用一个与旋转轴对齐的单位向量和一个单独的值来表示旋转角度（参见图示）。

图
图 3：泰特–布莱恩角，另一种描述方向的方法

　　 方向矩阵

　　 随着矩阵的引入，欧拉定理被重新表述。旋转被用正交矩阵描述，这些矩阵称为旋转矩阵或方向余弦矩阵。当用于表示方向时，旋转矩阵通常称为方向矩阵或姿态矩阵。

　　 上述的欧拉向量是旋转矩阵的特征向量（旋转矩阵有唯一的实特征值）。两个旋转矩阵的乘积即为旋转的组合。因此，和之前一样，方向可以表示为从初始参考系到达所需参考系的旋转。

　　 在 \( n \) 维空间中，非对称物体的配置空间为 \( \text{SO}(n) \times \mathbb{R}^n \)。可以通过将切向量的基附加到物体上来可视化方向，每个向量指向的方向决定了物体的方向。

　　 方向四元数

　　 另一种描述旋转的方法是使用旋转四元数，也称为单位四元数。它们等价于旋转矩阵和旋转向量。与旋转向量相比，它们可以更容易地与矩阵相互转换。当用于表示方向时，旋转四元数通常称为方向四元数或姿态四元数。

三维空间中的牛顿第二定律

　　 要在三维空间中考虑刚体动力学，必须扩展牛顿第二定律，以定义刚体的运动与作用在其上的力和力矩系统之间的关系。

　　 牛顿为单个粒子制定了他的第二定律，内容是：“物体的运动变化与所施加的力成正比，并且沿着施力的直线方向。”[3] 由于牛顿通常将质量乘以速度称为粒子的 “运动”，因此 “运动变化” 指的是粒子的质量乘以加速度，所以这条定律通常写作： \[ \mathbf{F} = m \mathbf{a},~ \] 其中 \( \mathbf{F} \) 被理解为作用在粒子上的唯一外力，\( m \) 是粒子的质量，\( \mathbf{a} \) 是其加速度向量。将牛顿第二定律扩展到刚体的方法是考虑一个刚性粒子系统。

刚性粒子系统

　　 如果一个由 \( N \) 个粒子 \( P_i \)（\( i=1, \dots, N \)）组成的系统形成一个刚体，则牛顿第二定律可以应用于该刚体中的每个粒子。如果 \( \mathbf{F}_i \) 是作用在质量为 \( m_i \) 的粒子 \( P_i \) 上的外力，则有： \[ \mathbf{F}_i + \sum_{j=1}^{N} \mathbf{F}_{ij} = m_i \mathbf{a}_i, \quad i = 1, \dots, N,~ \] 其中 \( \mathbf{F}_{ij} \) 是粒子 \( P_j \) 作用于粒子 \( P_i \) 的内力，用来维持这些粒子之间的固定距离。

图
图 4：人体被建模为几何实心的刚体系统。为更好地展示行走者的形态，添加了代表性的骨骼。

　　 通过引入作用在刚体系统上的合力和力矩，可以对这些力方程进行重要的简化。这个合力和力矩是通过选择系统中的一个粒子作为参考点 \( R \) 得到的，每个外力都施加在此参考点，并附加了相应的力矩。合力 \( \mathbf{F} \) 和力矩 \( \mathbf{T} \) 的公式为： \[ \mathbf{F} = \sum_{i=1}^{N} \mathbf{F}_{i}, \quad \mathbf{T} = \sum_{i=1}^{N} (\mathbf{R}_{i} - \mathbf{R}) \times \mathbf{F}_{i},~ \] 其中 \( \mathbf{R}_i \) 是定义粒子 \( P_i \) 位置的向量。

　　 将牛顿的粒子第二定律与合力和力矩的公式结合，得到： \[ \mathbf{F} = \sum_{i=1}^{N} m_{i} \mathbf{a}_{i}, \quad \mathbf{T} = \sum_{i=1}^{N} (\mathbf{R}_{i} - \mathbf{R}) \times (m_{i} \mathbf{a}_{i}),~ \] 其中内部力 \( \mathbf{F}_{ij} \) 成对抵消。刚体的运动学给出粒子 \( P_i \) 加速度的公式，该加速度基于参考粒子的位置 \( \mathbf{R} \) 和加速度 \( \mathbf{a} \)，以及刚体系统的角速度向量 \( \boldsymbol{\omega} \) 和角加速度向量 \( \boldsymbol{\alpha} \)： \[ \mathbf{a}_{i} = \boldsymbol{\alpha} \times (\mathbf{R}_{i} - \mathbf{R}) + \boldsymbol{\omega} \times (\boldsymbol{\omega} \times (\mathbf{R}_{i} - \mathbf{R})) + \mathbf{a}.~ \]

质量属性

　　 属性由其质心和惯性矩阵表示。选择参考点 \( R \)，使其满足以下条件： \[ \sum_{i=1}^{N} m_{i} (\mathbf{R}_{i} - \mathbf{R}) = 0,~ \] 那么 \( R \) 就被称为系统的质心。

　　 相对于参考点 \( R \) 的系统惯性矩阵 \([I_R]\) 定义为： \[ [I_{R}] = \sum_{i=1}^{N} m_{i} \left( \mathbf{I} (\mathbf{S}_{i}^{\textsf{T}} \mathbf{S}_{i}) - \mathbf{S}_{i} \mathbf{S}_{i}^{\textsf{T}} \right),~ \] 其中 \( \mathbf{S}_{i} \) 是列向量 \( \mathbf{R}_{i} - \mathbf{R} \)，\( \mathbf{S}_{i}^{\textsf{T}} \) 是其转置，\( \mathbf{I} \) 是 \( 3 \times 3 \) 的单位矩阵。

　　 \({\displaystyle \mathbf {S} _{i}^{\textsf {T}}\mathbf {S} _{i}}\) 是 \(\mathbf{S}_{i}\) 与其自身的标量积，而 \(\mathbf{S}_{i}\mathbf{S}_{i}^{\textsf {T}}\) 是 \(\mathbf{S}_{i}\) 与其自身的张量积。

力-力矩方程

　　 利用质心和惯性矩阵，单个刚体的力和力矩方程表示为： \[ \mathbf{F} = m \mathbf{a}, \quad \mathbf{T} = [I_{R}] \alpha + \omega \times [I_{R}] \omega,~ \] 这被称为刚体的牛顿第二运动定律。

　　 对于由 \( M \) 个刚体 \( B_j \)（\( j = 1, \dots, M \)）组成的互连系统，其动力学通过隔离每个刚体并引入相互作用力来进行描述。每个刚体上外力和相互作用力的合力给出力-力矩方程： \[ \mathbf{F}_{j} = m_{j} \mathbf{a}_{j}, \quad \mathbf{T}_{j} = [I_{R}]_{j} \alpha_{j} + \omega_{j} \times [I_{R}]_{j} \omega_{j}, \quad j = 1, \dots, M.~ \] 牛顿的表述给出 \( 6M \) 个方程，定义了 \( M \) 个刚体系统的动力学。[4]

三维旋转

　　 旋转物体在有无力矩影响下，都可能表现出进动和章动的行为。描述旋转刚体行为的基本方程是欧拉运动方程： \[ {\boldsymbol {\tau }} = \frac{D \mathbf{L}}{Dt} = \frac{d \mathbf{L}}{dt} + {\boldsymbol {\omega }} \times \mathbf{L} = \frac{d(I{\boldsymbol {\omega }})}{dt} + {\boldsymbol {\omega }} \times (I{\boldsymbol {\omega }}) = I{\boldsymbol {\alpha }} + {\boldsymbol {\omega }} \times (I{\boldsymbol {\omega }}),~ \] 其中伪向量 \(\boldsymbol{\tau}\) 和 \(\mathbf{L}\) 分别是作用在物体上的力矩和角动量，标量 \(I\) 是转动惯量，向量 \(\boldsymbol{\omega}\) 是角速度，\(\boldsymbol{\alpha}\) 是角加速度，\(D\) 是惯性参考系中的微分算符，\(d\) 是相对参考系（固定于物体）中的微分算符。

　　 无外加力矩时该方程的解在欧拉运动方程和泊松椭球体条目中讨论。

　　 由欧拉方程可知，当力矩 \(\boldsymbol{\tau}\) 垂直于旋转轴（即垂直于 \(\mathbf{L}\)）时，会产生绕 \(\boldsymbol{\tau}\) 和 \(\mathbf{L}\) 都垂直的轴的旋转。这种运动称为进动。进动的角速度 \(\Omega_{\mathrm{P}}\) 由叉积给出： \[ \boldsymbol{\tau} = \boldsymbol{\Omega}_{\mathrm{P}} \times \mathbf{L}.~ \]

图
图 5：陀螺仪的进动

　　 可以通过将一个旋转的陀螺水平放置，并在一端松散支撑（无摩擦地允许进动）来演示进动。预期陀螺可能会下落，但实际上它似乎 “抵抗” 重力，保持轴水平。当轴的另一端没有支撑，且自由端在水平面上缓慢画出一个圆时，陀螺表现出进动旋转。这一现象可以用上述方程来解释。陀螺上的力矩由一对力提供：重力向下作用在装置的质心上，以及支撑装置一端的等大向上力。由此力矩产生的旋转并非向下（直观上可能会导致陀螺下落），而是垂直于重力力矩（水平且垂直于旋转轴）和旋转轴（水平且向支点外）的方向，即绕垂直轴旋转，导致装置围绕支撑点缓慢旋转。

　　 在恒定力矩 \(\tau\) 的作用下，进动速度 \(\Omega_{\mathrm{P}}\) 与其角动量 \(L\) 成反比： \[ \tau = \Omega_{\mathrm{P}} L \sin \theta,~ \] 其中 \(\theta\) 是向量 \(\Omega_{\mathrm{P}}\) 和 \(L\) 之间的夹角。因此，如果陀螺的旋转速度减慢（例如由于摩擦），它的角动量减小，进动速率则增加。这种情况将持续到装置旋转速度不足以支撑其自身重量时，进动停止，陀螺掉落，主要是由于进动摩擦导致另一种进动，最终导致下落。

　　 根据惯例，这三个向量——力矩、旋转和进动——按照右手法则相互排列。

3. 作用在刚体上的力的虚功

　　 刚体动力学的另一种具有诸多便利特性的表述方法是通过考虑作用在刚体上的力的虚功来获得的。

　　 作用在单个刚体上不同点的力的虚功可以使用这些作用点的速度以及合力和力矩来计算。为了说明这一点，设力 \( \mathbf{F}_1, \mathbf{F}_2, \dots, \mathbf{F}_n \) 作用在刚体中的点 \( \mathbf{R}_1, \mathbf{R}_2, \dots, \mathbf{R}_n \) 上。

　　 这些点 \( \mathbf{R}_i \) 的轨迹由刚体的运动定义。点 \( \mathbf{R}_i \) 沿其轨迹的速度为： \[ \mathbf{V}_i = \boldsymbol{\omega} \times (\mathbf{R}_i - \mathbf{R}) + \mathbf{V},~ \] 其中 \( \boldsymbol{\omega} \) 是刚体的角速度向量。

虚功

　　 功可以通过每个力与其接触点位移的点积来计算： \[ \delta W = \sum_{i=1}^{n} \mathbf{F}_i \cdot \delta \mathbf{r}_i.~ \] 如果刚体的轨迹由一组广义坐标 \( q_j \)（\( j = 1, \dots, m \)）定义，则虚位移 \( \delta \mathbf{r}_i \) 为： \[ \delta \mathbf{r}_i = \sum_{j=1}^{m} \frac{\partial \mathbf{r}_i}{\partial q_j} \delta q_j = \sum_{j=1}^{m} \frac{\partial \mathbf{V}_i}{\partial \dot{q}_j} \delta q_j.~ \] 作用在物体上的这一系统的力在广义坐标下的虚功为： \[ \delta W = \mathbf{F}_1 \cdot \left( \sum_{j=1}^{m} \frac{\partial \mathbf{V}_1}{\partial \dot{q}_j} \delta q_j \right) + \dots + \mathbf{F}_n \cdot \left( \sum_{j=1}^{m} \frac{\partial \mathbf{V}_n}{\partial \dot{q}_j} \delta q_j \right).~ \] 或者将 \( \delta q_j \) 的系数收集起来： \[ \delta W = \left( \sum_{i=1}^{n} \mathbf{F}_i \cdot \frac{\partial \mathbf{V}_i}{\partial \dot{q}_1} \right) \delta q_1 + \dots + \left( \sum_{i=1}^{n} \mathbf{F}_i \cdot \frac{\partial \mathbf{V}_i}{\partial \dot{q}_m} \right) \delta q_m.~ \]

广义力

　　 为简单起见，考虑一个由单一广义坐标 \( q \)（例如旋转角度）指定的刚体轨迹，则公式变为： \[ \delta W = \left( \sum_{i=1}^{n} \mathbf{F}_i \cdot \frac{\partial \mathbf{V}_i}{\partial \dot{q}} \right) \delta q = \left( \sum_{i=1}^{n} \mathbf{F}_i \cdot \frac{\partial (\boldsymbol{\omega} \times (\mathbf{R}_i - \mathbf{R}) + \mathbf{V})}{\partial \dot{q}} \right) \delta q.~ \] 引入合力 \( \mathbf{F} \) 和力矩 \( \mathbf{T} \)，使该方程变为： \[ \delta W = \left( \mathbf{F} \cdot \frac{\partial \mathbf{V}}{\partial \dot{q}} + \mathbf{T} \cdot \frac{\partial \boldsymbol{\omega}}{\partial \dot{q}} \right) \delta q.~ \] 定义的量 \( Q \) 为： \[ Q = \mathbf{F} \cdot \frac{\partial \mathbf{V}}{\partial \dot{q}} + \mathbf{T} \cdot \frac{\partial \boldsymbol{\omega}}{\partial \dot{q}},~ \] 称为与虚位移 \( \delta q \) 相关的广义力。该公式可以推广到由多个广义坐标定义的刚体运动，即： \[ \delta W = \sum_{j=1}^{m} Q_j \delta q_j,~ \] 其中 \[ Q_j = \mathbf{F} \cdot \frac{\partial \mathbf{V}}{\partial \dot{q}_j} + \mathbf{T} \cdot \frac{\partial \boldsymbol{\omega}}{\partial \dot{q}_j}, \quad j=1, \dots, m.~ \] 值得注意的是，保守力（如重力和弹簧力）可以从势函数 \( V(q_1, \dots, q_n) \)（即势能）导出。在这种情况下，广义力为： \[ Q_j = -\frac{\partial V}{\partial q_j}, \quad j=1, \dots, m.~ \]

4. 达朗贝尔形式的虚功原理

　　 刚体机械系统的运动方程可以通过达朗贝尔形式的虚功原理来确定。虚功原理用于研究刚体系统的静态平衡，但通过在牛顿定律中引入加速度项，该方法被推广用于定义动态平衡。

静态平衡

　　 刚体机械系统的静态平衡定义为，在系统的任意虚位移下，所施加力的虚功为零。这就是所谓的虚功原理。[5] 这等价于任意虚位移下广义力为零的要求，即 \( Q_i = 0 \)。

　　 设一个机械系统由 \( n \) 个刚体 \( B_i \)（\( i = 1, \dots, n \)）组成，并设每个刚体上施加力的合力为力矩对 \( \mathbf{F}_i \) 和 \( \mathbf{T}_i \)（\( i = 1, \dots, n \)）。注意，这些施加的力不包括刚体连接处的反作用力。最后，假设每个刚体的速度 \( \mathbf{V}_i \) 和角速度 \( \boldsymbol{\omega}_i \)（\( i = 1, \dots, n \)）由一个广义坐标 \( q \) 定义。这样的刚体系统称为单自由度系统。

　　 作用在该单自由度系统上的力和力矩 \( \mathbf{F}_i \) 和 \( \mathbf{T}_i \) 的虚功为： \[ \delta W = \sum_{i=1}^{n} \left( \mathbf{F}_i \cdot \frac{\partial \mathbf{V}_i}{\partial \dot{q}} + \mathbf{T}_i \cdot \frac{\partial \boldsymbol{\omega}_i}{\partial \dot{q}} \right) \delta q = Q \delta q,~ \] 其中 \[ Q = \sum_{i=1}^{n} \left( \mathbf{F}_i \cdot \frac{\partial \mathbf{V}_i}{\partial \dot{q}} + \mathbf{T}_i \cdot \frac{\partial \boldsymbol{\omega}_i}{\partial \dot{q}} \right),~ \] 是作用在此单自由度系统上的广义力。

　　 如果机械系统由 \( m \) 个广义坐标 \( q_j \)（\( j = 1, \dots, m \)）定义，则系统具有 \( m \) 个自由度，虚功表示为： \[ \delta W = \sum_{j=1}^{m} Q_j \delta q_j,~ \] 其中 \[ Q_j = \sum_{i=1}^{n} \left( \mathbf{F}_i \cdot \frac{\partial \mathbf{V}_i}{\partial \dot{q}_j} + \mathbf{T}_i \cdot \frac{\partial \boldsymbol{\omega}_i}{\partial \dot{q}_j} \right), \quad j=1, \dots, m,~ \] 是与广义坐标 \( q_j \) 相关的广义力。虚功原理表明，静态平衡在系统上作用的这些广义力为零时发生，即 \[ Q_j = 0, \quad j=1, \dots, m.~ \] 这 \( m \) 个方程定义了刚体系统的静态平衡。

广义惯性力

　　 考虑一个在合力 \( \mathbf{F} \) 和力矩 \( \mathbf{T} \) 作用下运动的单个刚体，其运动由一个广义坐标 \( q \) 定义的单自由度描述。假设合力和力矩的参考点是物体的质心，那么与广义坐标 \( q \) 相关的广义惯性力 \( Q^* \) 给出为： \[ Q^* = - (M \mathbf{A}) \cdot \frac{\partial \mathbf{V}}{\partial \dot{q}} - \left( [I_R] \boldsymbol{\alpha} + \boldsymbol{\omega} \times [I_R] \boldsymbol{\omega} \right) \cdot \frac{\partial \boldsymbol{\omega}}{\partial \dot{q}}.~ \] 此惯性力可以通过刚体的动能来计算： \[ T = \frac{1}{2} M \mathbf{V} \cdot \mathbf{V} + \frac{1}{2} \boldsymbol{\omega} \cdot [I_R] \boldsymbol{\omega},~ \] 并使用以下公式： \[ Q^* = - \left( \frac{d}{dt} \frac{\partial T}{\partial \dot{q}} - \frac{\partial T}{\partial q} \right).~ \] 对于具有 \( m \) 个广义坐标的 \( n \) 个刚体系统，其动能为： \[ T = \sum_{i=1}^{n} \left( \frac{1}{2} M \mathbf{V}_i \cdot \mathbf{V}_i + \frac{1}{2} \boldsymbol{\omega}_i \cdot [I_R] \boldsymbol{\omega}_i \right),~ \] 该动能可用于计算 \( m \) 个广义惯性力： \[ Q_j^* = - \left( \frac{d}{dt} \frac{\partial T}{\partial \dot{q}_j} - \frac{\partial T}{\partial q_j} \right), \quad j = 1, \dots, m.~ \]

动态平衡

　　 达朗贝尔形式的虚功原理指出，当刚体系统的作用力和惯性力之和的虚功对于系统的任意虚位移为零时，该系统处于动态平衡。因此，具有 \( m \) 个广义坐标的 \( n \) 个刚体系统的动态平衡要求： \[ \delta W = \left(Q_{1} + Q_{1}^{*}\right) \delta q_{1} + \dots + \left(Q_{m} + Q_{m}^{*}\right) \delta q_{m} = 0,~ \] 对于任意虚位移集 \( \delta q_j \)。这一条件得出 \( m \) 个方程： \[ Q_j + Q_j^* = 0, \quad j = 1, \dots, m,~ \] 这也可以写成： \[ \frac{d}{dt} \frac{\partial T}{\partial \dot{q}_j} - \frac{\partial T}{\partial q_j} = Q_j, \quad j = 1, \dots, m.~ \] 结果是一组 \( m \) 个运动方程，用于定义刚体系统的动力学。

拉格朗日方程

　　 如果广义力 \( Q_j \) 可由势能 \( V(q_1, \dots, q_m) \) 导出，则这些运动方程可以表示为： \[ \frac{d}{dt} \frac{\partial T}{\partial \dot{q}_j} - \frac{\partial T}{\partial q_j} = -\frac{\partial V}{\partial q_j}, \quad j = 1, \dots, m.~ \] 在这种情况下，引入拉格朗日量 \( L = T - V \)，使这些运动方程变为： \[ \frac{d}{dt} \frac{\partial L}{\partial \dot{q}_j} - \frac{\partial L}{\partial q_j} = 0, \quad j = 1, \dots, m.~ \] 这些方程称为拉格朗日运动方程。

5. 线性和角动量

粒子系统

　　 刚体粒子系统的线性和角动量是通过测量粒子相对于质心的位置和速度来定义的。设粒子系统 \( P_i \)（\( i = 1, \dots, n \)）位于坐标 \( \mathbf{r}_i \) 处，速度为 \( \mathbf{v}_i \)。选择一个参考点 \( \mathbf{R} \)，并计算相对位置和速度向量。 \[ \mathbf{r}_i = \left(\mathbf{r}_i - \mathbf{R}\right) + \mathbf{R}, \quad \mathbf{v}_i = \frac{d}{dt}(\mathbf{r}_i - \mathbf{R}) + \mathbf{V}.~ \] 相对于参考点 \( \mathbf{R} \) 的总线性动量和角动量向量分别为： \[ \mathbf{p} = \frac{d}{dt} \left( \sum_{i=1}^{n} m_i \left( \mathbf{r}_i - \mathbf{R} \right) \right) + \left( \sum_{i=1}^{n} m_i \right) \mathbf{V},~ \] 以及 \[ \mathbf{L} = \sum_{i=1}^{n} m_i \left( \mathbf{r}_i - \mathbf{R} \right) \times \frac{d}{dt} \left( \mathbf{r}_i - \mathbf{R} \right) + \left( \sum_{i=1}^{n} m_i \left( \mathbf{r}_i - \mathbf{R} \right) \right) \times \mathbf{V}.~ \] 如果选择 \( \mathbf{R} \) 为质心，则这些方程简化为： \[ \mathbf{p} = M \mathbf{V}, \quad \mathbf{L} = \sum_{i=1}^{n} m_i \left( \mathbf{r}_i - \mathbf{R} \right) \times \frac{d}{dt} \left( \mathbf{r}_i - \mathbf{R} \right).~ \]

刚性粒子系统

　　 为了将这些公式专门化用于刚体，假设粒子是刚性连接在一起的，因此 \( P_i \)（\( i = 1, \dots, n \)）的坐标为 \( \mathbf{r}_i \)，速度为 \( \mathbf{v}_i \)。选择一个参考点 \( \mathbf{R} \)，计算相对位置和速度向量： \[ \mathbf{r}_i = (\mathbf{r}_i - \mathbf{R}) + \mathbf{R}, \quad \mathbf{v}_i = \omega \times (\mathbf{r}_i - \mathbf{R}) + \mathbf{V},~ \] 其中 \( \omega \) 为系统的角速度。

　　 相对于质心 \( \mathbf{R} \) 的线动量和角动量为： \[ \mathbf{p} = \left( \sum_{i=1}^{n} m_i \right) \mathbf{V},~ \] \[ \mathbf{L} = \sum_{i=1}^{n} m_i (\mathbf{r}_i - \mathbf{R}) \times \mathbf{v}_i = \sum_{i=1}^{n} m_i (\mathbf{r}_i - \mathbf{R}) \times (\omega \times (\mathbf{r}_i - \mathbf{R})).~ \] 这些方程可以简化为： \[ \mathbf{p} = M \mathbf{V}, \quad \mathbf{L} = [I_R] \omega,~ \]

　　 其中 \( M \) 是系统的总质量，且 \( [I_R] \) 是由以下定义的惯性矩阵： \[ [I_R] = -\sum_{i=1}^{n} m_i [r_i - R][r_i - R],~ \] 其中 \( [r_i - R] \) 是由向量 \( \mathbf{r}_i - \mathbf{R} \) 构造的反对称矩阵。

6. 应用

7. 参见

8. 参考文献

　　
1. B. Paul, 《平面机械的运动学与动力学》，普伦蒂斯-霍尔出版社，新泽西州，1979 年。
2. L. W. Tsai, 《机器人分析：串联和并联操纵器的力学》，约翰-威利出版社，纽约，1999 年。
3. 《大英百科全书》，[牛顿运动定律](https://www.britannica.com/science/Newtons-laws-of-motion)。
4. K. J. Waldron 和 G. L. Kinzel，《机械设计中的运动学与动力学》，第 2 版，约翰-威利父子出版社，2004 年。
5. Torby, Bruce (1984 年). 《能量方法》。高级工程动力学。HRW 机械工程系列。美国：CBS 大学出版社。ISBN 0-03-063366-4。
6. T. R. Kane 和 D. A. Levinson，《动力学，理论与应用》，麦格劳-希尔出版社，纽约，2005 年。
7. Marion, JB; Thornton, ST (1995 年). 《系统与粒子的经典动力学》(第 4 版)。汤姆森出版。ISBN 0-03-097302-3。
8. Symon, KR (1971 年). 《力学》(第 3 版). 艾迪生-韦斯利出版社。ISBN 0-201-07392-7。
9. Tenenbaum, RA (2004 年). 《应用动力学基础》。施普林格出版社。ISBN 0-387-00887-X。
10. Gomez, R W; Hernandez-Gomez, J J; Marquina, V (2012 年 7 月 25 日). "倾斜平面上跳跃的圆柱体"。《欧洲物理杂志》。33 (5). IOP: 1359–1365. [arXiv:1204.0600](https://arxiv.org/abs/1204.0600)。Bibcode:2012EJPh...33.1359G. [doi:10.1088/0143-0807/33/5/1359](https://doi.org/10.1088/0143-0807/33/5/1359). S2CID 55442794。检索日期：2016 年 4 月 25 日。

9. 延伸阅读

                     

© 小时科技 保留一切权利