哈密顿力学（综述）

贡献者：待更新

　　本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章）

图 1：威廉·罗恩·哈密顿爵士

　　在物理学中，哈密顿力学是拉格朗日力学的重新表述，起源于 1833 年。由威廉·罗恩·哈密顿爵士提出【1】，哈密顿力学用（广义）动量替代了拉格朗日力学中使用的（广义）速度 \( \dot{q}^i \)。这两种理论都提供了对经典力学的解释，并描述了相同的物理现象。

　　哈密顿力学与几何学（特别是辛几何和泊松结构）有密切关系，并且作为经典力学与量子力学之间的纽带。

1. 概述

相空间坐标 \( (p, q) \) 和哈密顿量 \( H \)

　　设 \( (M, \mathcal{L}) \) 为一个具有构型空间 \( M \) 和光滑拉格朗日量 \( \mathcal{L} \) 的力学系统。选择 \( M \) 上的标准坐标系 \( (\boldsymbol{q}, \boldsymbol{\dot{q}}) \)。量 \( p_i(\boldsymbol{q}, \boldsymbol{\dot{q}}, t) \stackrel{\text{def}}{=} \partial \mathcal{L} / \partial \dot{q}^i \) 称为动量（也称为广义动量、共轭动量或正则动量）。对于时间瞬间 \( t \)，拉格朗日量 \( \mathcal{L} \) 的勒让德变换定义为映射 \( (\boldsymbol{q}, \boldsymbol{\dot{q}}) \to (\boldsymbol{p}, \boldsymbol{q}) \)，假设其具有光滑逆映射 \( (\boldsymbol{p}, \boldsymbol{q}) \to (\boldsymbol{q}, \boldsymbol{\dot{q}}) \)。对于具有 \( n \) 个自由度的系统，拉格朗日力学定义了能量函数 \[ E_{\mathcal{L}}(\boldsymbol{q}, \boldsymbol{\dot{q}}, t) \stackrel{\text{def}}{=} \sum_{i=1}^{n} \dot{q}^i \frac{\partial \mathcal{L}}{\partial \dot{q}^i} - \mathcal{L} ~. \] 拉格朗日量 \( \mathcal{L} \) 的勒让德变换将 \( E_{\mathcal{L}} \) 转化为称为哈密顿量的函数 \( \mathcal{H}(\boldsymbol{p}, \boldsymbol{q}, t) \)。哈密顿量满足： \[ \mathcal{H}\left(\frac{\partial \mathcal{L}}{\partial \boldsymbol{\dot{q}}}, \boldsymbol{q}, t\right) = E_{\mathcal{L}}(\boldsymbol{q}, \boldsymbol{\dot{q}}, t)~ \] 这意味着： \[ \mathcal{H}(\boldsymbol{p}, \boldsymbol{q}, t) = \sum_{i=1}^{n} p_i \dot{q}^i - \mathcal{L}(\boldsymbol{q}, \boldsymbol{\dot{q}}, t),~ \] 其中速度 \( \boldsymbol{\dot{q}} = (\dot{q}^1, \dots, \dot{q}^n) \) 从 \( \boldsymbol{p} = \partial \mathcal{L} / \partial \boldsymbol{\dot{q}} \)（一个 \( n \) 维方程组）中得出，假设它对于 \( \boldsymbol{\dot{q}} \) 的解是唯一的。\( ( \boldsymbol{p}, \boldsymbol{q} ) \)（一个 \( 2n \) 维对）称为相空间坐标（也称为正则坐标）。

从欧拉-拉格朗日方程到哈密顿方程

　　在相空间坐标 \( (\boldsymbol{p}, \boldsymbol{q}) \) 中，\( n \) 维的欧拉-拉格朗日方程 \[ \frac{\partial \mathcal{L}}{\partial \boldsymbol{q}} - \frac{d}{dt} \frac{\partial \mathcal{L}}{\partial \boldsymbol{\dot{q}}} = 0~ \] 变为 \( 2n \) 维的哈密顿方程： \[ \frac{d \boldsymbol{q}}{dt} = \frac{\partial \mathcal{H}}{\partial \boldsymbol{p}}, \quad \frac{d \boldsymbol{p}}{dt} = -\frac{\partial \mathcal{H}}{\partial \boldsymbol{q}}.~ \] 证明

　　哈密顿量 \( \mathcal{H}(\boldsymbol{p}, \boldsymbol{q}) \) 是拉格朗日量 \( \mathcal{L}(\boldsymbol{q}, \boldsymbol{\dot{q}}) \) 的勒让德变换，因此有： \[ \mathcal{L}(\boldsymbol{q}, \boldsymbol{\dot{q}}) + \mathcal{H}(\boldsymbol{p}, \boldsymbol{q}) = \boldsymbol{p} \cdot \boldsymbol{\dot{q}}~ \] 因此 \[ \partial \mathcal{H}/\partial \boldsymbol{p} = \boldsymbol{\dot{q}}, \quad \partial \mathcal{L}/\partial \boldsymbol{q} = -\partial \mathcal{H}/\partial \boldsymbol{q}.~ \] 此外，由于 \( \boldsymbol{p} = \frac{\partial \mathcal{L}}{\partial \boldsymbol{\dot{q}}} \)，欧拉-拉格朗日方程给出 \[ d \boldsymbol{p}/dt = \partial \mathcal{L}/\partial \boldsymbol{q} = -\partial \mathcal{H}/\partial \boldsymbol{q}.~ \]

从驻定作用量原理到哈密顿方程

　　设 \( \mathcal{P}(a, b, \boldsymbol{x}_a, \boldsymbol{x}_b) \) 为满足 \( \boldsymbol{q}(a) = \boldsymbol{x}_a \) 和 \( \boldsymbol{q}(b) = \boldsymbol{x}_b \) 的光滑路径集合 \( \boldsymbol{q}: [a, b] \to M \)。作用泛函 \( \mathcal{S}: \mathcal{P}(a, b, \boldsymbol{x}_a, \boldsymbol{x}_b) \to \mathbb{R} \) 定义为 \[ \mathcal{S}[\boldsymbol{q}] = \int_a^b \mathcal{L}(t, \boldsymbol{q}(t), \dot{\boldsymbol{q}}(t)) \, dt = \int_a^b \left(\sum_{i=1}^n p_i \dot{q}^i - \mathcal{H}(\boldsymbol{p}, \boldsymbol{q}, t)\right) \, dt,~ \] 其中 \( \boldsymbol{q} = \boldsymbol{q}(t) \)，且 \( \boldsymbol{p} = \partial \mathcal{L} / \partial \boldsymbol{\dot{q}} \)（见上文）。若路径 \( \boldsymbol{q} \in \mathcal{P}(a, b, \boldsymbol{x}_a, \boldsymbol{x}_b) \) 为 \( \mathcal{S} \) 的驻点（因此满足运动方程），则相空间坐标 \( (\boldsymbol{p}(t), \boldsymbol{q}(t)) \) 必须满足哈密顿方程。

基本物理解释

　　对哈密顿力学的简单解释来自其在由质量为 \( m \) 的单个非相对论粒子组成的一维系统中的应用。此情况下，哈密顿量 \( H(p, q) \) 的值是系统的总能量，即动能和势能之和，分别传统地表示为 \( T \) 和 \( V \)。其中 \( p \) 是动量 \( mv \)，而 \( q \) 是空间坐标。则有： \[ \mathcal{H} = T + V, \quad T = \frac{p^2}{2m}, \quad V = V(q)~ \] 动能 \( T \) 仅为 \( p \) 的函数，而势能 \( V \) 仅为 \( q \) 的函数（即 \( T \) 和 \( V \) 是非时间依赖的）。

　　在此示例中，\( q \) 的时间导数是速度，因此第一哈密顿方程意味着粒子的速度等于其动能对动量的导数。动量 \( p \) 的时间导数等于牛顿力，因此第二哈密顿方程意味着力等于势能的负梯度。

2. 示例

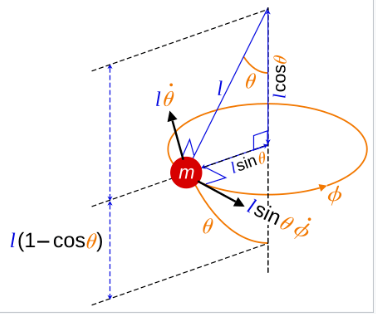
　　球面摆由一个质量为 \( m \) 的物体组成，其在球面上无摩擦地运动。作用在该质量上的唯一力是球面的反作用力和重力。使用球坐标 \( (r, \theta, \phi) \) 来描述该质量的位置，其中 \( r \) 是固定的，\( r = \ell \)。

图 2：球面摆：角度和速度。

　　该系统的拉格朗日量为【2】： \[ L = \frac{1}{2}m\ell^2\left(\dot{\theta}^2 + \sin^2 \theta \, \dot{\varphi}^2\right) + mg\ell \cos \theta.~ \] 因此，哈密顿量为 \[ H = P_{\theta} \dot{\theta} + P_{\varphi} \dot{\varphi} - L~ \] 其中 \[ P_{\theta} = \frac{\partial L}{\partial \dot{\theta}} = m\ell^2 \dot{\theta}~ \] 和 \[ P_{\varphi} = \frac{\partial L}{\partial \dot{\varphi}} = m\ell^2 \sin^2 \theta \, \dot{\varphi}.~ \] 用坐标和动量表示时，哈密顿量为 \[ H = \underbrace{\left[\frac{1}{2}m\ell^2 \dot{\theta}^2 + \frac{1}{2}m\ell^2 \sin^2 \theta \, \dot{\varphi}^2 \right]}_{T} + \underbrace{\left[-mg\ell \cos \theta \right]}_{V} = \frac{P_{\theta}^2}{2m\ell^2} + \frac{P_{\varphi}^2}{2m\ell^2 \sin^2 \theta} - mg\ell \cos \theta.~ \] 哈密顿方程给出了坐标和共轭动量的时间演化，这些是一组四个一阶微分方程： \[ \begin{aligned} \dot{\theta} &= \frac{P_{\theta}}{m\ell^2}, \\ \dot{\varphi} &= \frac{P_{\varphi}}{m\ell^2 \sin^2 \theta}, \\ \dot{P_{\theta}} &= \frac{P_{\varphi}^2}{m\ell^2 \sin^3 \theta} \cos \theta - mg\ell \sin \theta, \\ \dot{P_{\varphi}} &= 0. \end{aligned}~ \] 动量 \( P_{\varphi} \) 对应于角动量的垂直分量 \( L_z = \ell \sin \theta \times m\ell \sin \theta \, \dot{\varphi} \)，是一个守恒量。这是系统围绕垂直轴旋转对称性的结果。由于方位角 \( \varphi \) 不出现在哈密顿量中，因此它是一个循环坐标，这意味着其共轭动量守恒。

3. 推导哈密顿方程

　　哈密顿方程可以通过拉格朗日量 \( \mathcal{L} \)、广义位置 \( q^i \) 和广义速度 \( \dot{q}^i \) 的计算推导出来，其中 \( i = 1, \ldots, n \)【3】。这里我们在 “非壳” 情况下工作，意味着 \( q^i \)、\( \dot{q}^i \)、\( t \) 是相空间中的独立坐标，不受任何运动方程的约束（特别是 \( \dot{q}^i \) 不是 \( q^i \) 的导数）。拉格朗日量的全微分为： \[ \mathrm{d} \mathcal{L} = \sum_{i} \left( \frac{\partial \mathcal{L}}{\partial q^i} \, \mathrm{d} q^i + \frac{\partial \mathcal{L}}{\partial \dot{q}^i} \, \mathrm{d} \dot{q}^i \right) + \frac{\partial \mathcal{L}}{\partial t} \, \mathrm{d} t.~ \] 广义动量坐标定义为 \( p_i = \frac{\partial \mathcal{L}}{\partial \dot{q}^i} \)，因此我们可以将方程改写为： \[ \mathrm{d} \mathcal{L} = \sum_{i} \left( \frac{\partial \mathcal{L}}{\partial q^i} \, \mathrm{d} q^i + p_i \, \mathrm{d} \dot{q}^i \right) + \frac{\partial \mathcal{L}}{\partial t} \, \mathrm{d} t = \sum_{i} \left( \frac{\partial \mathcal{L}}{\partial q^i} \, \mathrm{d} q^i + \mathrm{d} (p_i \dot{q}^i) - \dot{q}^i \, \mathrm{d} p_i \right) + \frac{\partial \mathcal{L}}{\partial t} \, \mathrm{d} t.~ \] 重新排列后得到： \[ \mathrm{d} \left(\sum_{i} p_i \dot{q}^i - \mathcal{L}\right) = \sum_{i} \left( -\frac{\partial \mathcal{L}}{\partial q^i} \, \mathrm{d} q^i + \dot{q}^i \, \mathrm{d} p_i \right) - \frac{\partial \mathcal{L}}{\partial t} \, \mathrm{d} t.~ \] 左侧括号中的项即为之前定义的哈密顿量 \( \mathcal{H} = \sum p_i \dot{q}^i - \mathcal{L} \)，因此： \[ \mathrm{d} \mathcal{H} = \sum_{i} \left( -\frac{\partial \mathcal{L}}{\partial q^i} \, \mathrm{d} q^i + \dot{q}^i \, \mathrm{d} p_i \right) - \frac{\partial \mathcal{L}}{\partial t} \, \mathrm{d} t.~ \] 也可以计算哈密顿量 \( \mathcal{H} \) 相对于坐标 \( q^i \)、\( p_i \)、\( t \) 的全微分，而不是相对于 \( q^i \)、\( \dot{q}^i \)、\( t \)，得到： \[ \mathrm{d} \mathcal{H} = \sum_{i} \left( \frac{\partial \mathcal{H}}{\partial q^i} \, \mathrm{d} q^i + \frac{\partial \mathcal{H}}{\partial p_i} \, \mathrm{d} p_i \right) + \frac{\partial \mathcal{H}}{\partial t} \, \mathrm{d} t.~ \] 现在，可以将 \( \mathrm{d}\mathcal{H} \) 的两个表达式等式化，一个关于 \( \mathcal{L} \)，另一个关于 \( \mathcal{H} \)： \[ \sum_{i} \left( -\frac{\partial \mathcal{L}}{\partial q^i} \, \mathrm{d} q^i + \dot{q}^i \, \mathrm{d} p_i \right) - \frac{\partial \mathcal{L}}{\partial t} \, \mathrm{d} t = \sum_{i} \left( \frac{\partial \mathcal{H}}{\partial q^i} \, \mathrm{d} q^i + \frac{\partial \mathcal{H}}{\partial p_i} \, \mathrm{d} p_i \right) + \frac{\partial \mathcal{H}}{\partial t} \, \mathrm{d} t.~ \] 由于这些计算是在 “非壳” 情况下完成的，可以将等式两边的 \( \mathrm{d} q^i \)、\( \mathrm{d} p_i \)、\( \mathrm{d} t \) 的系数分别相等，得到： \[ \frac{\partial \mathcal{H}}{\partial q^i} = -\frac{\partial \mathcal{L}}{\partial q^i}, \quad \frac{\partial \mathcal{H}}{\partial p_i} = \dot{q}^i, \quad \frac{\partial \mathcal{H}}{\partial t} = -\frac{\partial \mathcal{L}}{\partial t}.~ \] 在 “壳” 上，替换参数化函数 \( q^i = q^i(t) \) 来定义相空间中的轨迹，其速度为 \( \dot{q}^i = \frac{d}{dt} q^i(t) \)，满足拉格朗日方程： \[ \frac{d}{dt} \frac{\partial \mathcal{L}}{\partial \dot{q}^i} - \frac{\partial \mathcal{L}}{\partial q^i} = 0.~ \] 重新排列并用 “壳” 上的 \( p_i = p_i(t) \) 表示得到： \[ \frac{\partial \mathcal{L}}{\partial q^i} = \dot{p}_i.~ \] 因此，拉格朗日方程等价于哈密顿方程： \[ \frac{\partial \mathcal{H}}{\partial q^i} = -\dot{p}_i, \quad \frac{\partial \mathcal{H}}{\partial p_i} = \dot{q}^i, \quad \frac{\partial \mathcal{H}}{\partial t} = -\frac{\partial \mathcal{L}}{\partial t}.~ \] 在哈密顿量 \( \mathcal{H} \) 和拉格朗日量 \( \mathcal{L} \) 都不依赖于时间的情况下，即 \(\frac{\partial \mathcal{H}}{\partial t} = -\frac{\partial \mathcal{L}}{\partial t} = 0\),哈密顿方程组成了 \( 2n \) 个一阶微分方程，而拉格朗日方程是 \( n \) 个二阶方程。尽管哈密顿方程通常不会减少求显式解的难度，但它们可以用于推导出重要的理论结果，因为坐标和动量是独立变量，具有近乎对称的作用。

　　哈密顿方程相比于拉格朗日方程有另一个优势：如果一个系统具有对称性，使得某个坐标 \( q_i \) 不出现在哈密顿量中（即这是一个循环坐标），那么对应的动量坐标 \( p_i \) 沿每条轨迹保持守恒，并且在该方程组的其他方程中可以将该坐标简化为常数。这有效地将问题从 \( n \) 个坐标减少到 \( n - 1 \) 个坐标：这是几何学中辛约简的基础。在拉格朗日框架中，动量守恒同样可以立即得出，但所有的广义速度 \( \dot{q}_i \) 仍然出现在拉格朗日量中，因此仍需在 \( n \) 个坐标中求解一个方程组。

　　拉格朗日和哈密顿的方法为经典力学中的更深层次结果奠定了基础，并暗示了量子力学中的类似表述：即路径积分表述和薛定谔方程。

哈密顿量 \( \mathcal{H} \) 的性质如下：

当且仅当能量函数 \( E_{\mathcal{L}} \) 具有相同性质时，哈密顿量 \( \mathcal{H} \) 的值等于系统的总能量。（参见 \( \mathcal{H} \) 的定义。）
\[\frac{d\mathcal{H}}{dt} = \frac{\partial \mathcal{H}}{\partial t}~\]当 \( \mathbf{p}(t) \) 和 \( \mathbf{q}(t) \) 形成哈密顿方程的解时成立。实际上，\[\frac{d\mathcal{H}}{dt} = \frac{\partial \mathcal{H}}{\partial \mathbf{p}} \cdot \dot{\mathbf{p}} + \frac{\partial \mathcal{H}}{\partial \mathbf{q}} \cdot \dot{\mathbf{q}} + \frac{\partial \mathcal{H}}{\partial t}~,\]其中除最后一项外，其余项均相互抵消。
\( \mathcal{H} \) 在点变换下保持不变，即平滑的坐标变化 \( \mathbf{q} \leftrightarrow \mathbf{q'} \) 不改变 \( \mathcal{H} \)。（这一点源于能量函数 \( E_{\mathcal{L}} \) 在点变换下的不变性。可以直接验证 \( E_{\mathcal{L}} \) 的不变性。）
\[\frac{\partial \mathcal{H}}{\partial t} = -\frac{\partial \mathcal{L}}{\partial t}.~\]（见 “推导哈密顿方程” 部分。）
\[-\frac{\partial \mathcal{H}}{\partial q^{i}} = \dot{p}_{i} = \frac{\partial \mathcal{L}}{\partial q^{i}}.~\]（比较哈密顿方程和欧拉-拉格朗日方程，或参见 “推导哈密顿方程” 部分。）
\[\frac{\partial \mathcal{H}}{\partial q^{i}} = 0~\]当且仅当\[\frac{\partial \mathcal{L}}{\partial q^{i}} = 0~\]。满足最后一个方程的坐标称为循环坐标（或可忽略坐标）。每个循环坐标 \( q^{i} \) 都会将自由度数量减少 1，使得相应的动量 \( p_{i} \) 得到守恒，并使得哈密顿方程的求解更为简便。

4. 哈密顿量作为系统的总能量：

　　在应用于特定系统时，哈密顿量通常取为 \[ \mathcal{H} = T + V~ \] 其中 \( T \) 是动能，\( V \) 是势能。直接使用此关系有时比先计算拉格朗日量再从中导出哈密顿量更简单。然而，这一关系并不适用于所有系统。

　　对于非相对论系统，当下列条件都满足时，这一关系成立【5】【6】： \[ \frac{\partial V(\mathbf{q}, \mathbf{\dot{q}}, t)}{\partial \dot{q}_i} = 0,\quad \forall i~ \] \[ \frac{\partial T(\mathbf{q}, \mathbf{\dot{q}}, t)}{\partial t} = 0~ \] \[ T(\mathbf{q}, \mathbf{\dot{q}}) = \sum_{i=1}^{n}\sum_{j=1}^{n} \left( c_{ij}(\mathbf{q}) \dot{q}_i \dot{q}_j \right)~ \] 其中 \( t \) 是时间，\( n \) 是系统的自由度数量，每个 \( c_{ij}(\mathbf{q}) \) 是 \( \mathbf{q} \) 的任意标量函数。

　　通俗地说，这意味着关系 \( \mathcal{H} = T + V \) 成立的条件是：动能 \( T \) 不显含时间（即它是定态的），势能 \( V \) 不显含广义速度，并且动能 \( T \) 的每一项在广义速度中都是二次项。

证明

　　在进行本证明之前，有必要先解决相关数学符号中的一个歧义。虽然可以通过变量变换将 \[ \mathcal{L}(\boldsymbol{p}, \boldsymbol{q}, t) = \mathcal{L}(\boldsymbol{q}, \boldsymbol{\dot{q}}, t)~ \] 相等，但需要注意的是 \[ \frac{\partial \mathcal{L}(\boldsymbol{q}, \boldsymbol{\dot{q}}, t)}{\partial \dot{q}_i} \neq \frac{\partial \mathcal{L}(\boldsymbol{p}, \boldsymbol{q}, t)}{\partial \dot{q}_i}~ \] 在这种情况下，右侧总是等于 0。若要在偏导数中执行变量变换，应使用多变量链式法则。因此，为避免歧义，应在任何偏导数内的项中标明函数的参数。

　　另外，此证明中使用了符号 \[ f(a, b, c) = f(a, b)~ \] 以暗示 \[ \frac{\partial f(a, b, c)}{\partial c} = 0~ \] 证明

　　从具有 \( n \) 个自由度系统的哈密顿量、广义动量和拉格朗日量的定义开始： \[ \mathcal{H} = \sum_{i=1}^{n} \left( p_{i} \dot{q}_{i} \right) - \mathcal{L}(\boldsymbol{q}, \boldsymbol{\dot{q}}, t)~ \] 广义动量的定义为： \[ p_{i}(\boldsymbol{q}, \boldsymbol{\dot{q}}, t) = \frac{\partial \mathcal{L}(\boldsymbol{q}, \boldsymbol{\dot{q}}, t)}{\partial \dot{q}_{i}}~ \] 拉格朗日量表示为： \[ \mathcal{L}(\boldsymbol{q}, \boldsymbol{\dot{q}}, t) = T(\boldsymbol{q}, \boldsymbol{\dot{q}}, t) - V(\boldsymbol{q}, \boldsymbol{\dot{q}}, t)~ \] 其中 \( T \) 是系统的动能，\( V \) 是势能。

　　将广义动量代入哈密顿量得到： \[ \mathcal{H} = \sum_{i=1}^{n} \left( \frac{\partial \mathcal{L}(\boldsymbol{q}, \boldsymbol{\dot{q}}, t)}{\partial \dot{q}_{i}} \dot{q}_{i} \right) - \mathcal{L}(\boldsymbol{q}, \boldsymbol{\dot{q}}, t)~ \] 将拉格朗日量代入结果得到： \[ \mathcal{H} = \sum_{i=1}^{n} \left( \frac{\partial \left(T(\boldsymbol{q}, \boldsymbol{\dot{q}}, t) - V(\boldsymbol{q}, \boldsymbol{\dot{q}}, t)\right)}{\partial \dot{q}_{i}} \dot{q}_{i} \right) - \left(T(\boldsymbol{q}, \boldsymbol{\dot{q}}, t) - V(\boldsymbol{q}, \boldsymbol{\dot{q}}, t)\right)~ \] \[ = \sum_{i=1}^{n} \left( \frac{\partial T(\boldsymbol{q}, \boldsymbol{\dot{q}}, t)}{\partial \dot{q}_{i}} \dot{q}_{i} - \frac{\partial V(\boldsymbol{q}, \boldsymbol{\dot{q}}, t)}{\partial \dot{q}_{i}} \dot{q}_{i} \right) - T(\boldsymbol{q}, \boldsymbol{\dot{q}}, t) + V(\boldsymbol{q}, \boldsymbol{\dot{q}}, t)~ \] 现在假设： \[ \frac{\partial V(\boldsymbol{q}, \boldsymbol{\dot{q}}, t)}{\partial \dot{q}_{i}} = 0, \quad \forall i~ \] 并且假设： \[ \frac{\partial T(\boldsymbol{q}, \boldsymbol{\dot{q}}, t)}{\partial t} = 0~ \] 应用这些假设得到：

\begin{equation} \begin{aligned} \mathcal{H} &= \sum_{i=1}^{n} \left( \frac{\partial T(\boldsymbol{q}, \boldsymbol{\dot{q}})}{\partial \dot{q}_{i}} \dot{q}_{i} - \frac{\partial V(\boldsymbol{q}, t)}{\partial \dot{q}_{i}} \dot{q}_{i} \right) - T(\boldsymbol{q}, \boldsymbol{\dot{q}}) + V(\boldsymbol{q}, t)\\ &= \sum_{i=1}^{n} \left( \frac{\partial T(\boldsymbol{q}, \boldsymbol{\dot{q}})}{\partial \dot{q}_{i}} \dot{q}_{i} \right) - T(\boldsymbol{q}, \boldsymbol{\dot{q}}) + V(\boldsymbol{q}, t) \end{aligned}~ \end{equation}

接下来假设 \( T \) 的形式为： \[ T(\boldsymbol{q}, \boldsymbol{\dot{q}}) = \sum_{i=1}^{n} \sum_{j=1}^{n} \left( c_{ij}(\boldsymbol{q}) \dot{q}_{i} \dot{q}_{j} \right)~ \] 其中每个 \( c_{ij}(\boldsymbol{q}) \) 是关于 \( \boldsymbol{q} \) 的任意标量函数。

　　对 \( \dot{q}_{l} \) 求导，其中 \( l \in [1, n] \)，得到：

\begin{equation} \begin{aligned} \frac{\partial T(\boldsymbol{q}, \boldsymbol{\dot{q}})}{\partial \dot{q}_{l}} &= \sum_{i=1}^{n} \sum_{j=1}^{n} \left( \frac{\partial \left[ c_{ij}(\boldsymbol{q}) \dot{q}_{i} \dot{q}_{j} \right]}{\partial \dot{q}_{l}} \right)\\ &= \sum_{i=1}^{n} \sum_{j=1}^{n} \left( c_{ij}(\boldsymbol{q}) \frac{\partial \left[ \dot{q}_{i} \dot{q}_{j} \right]}{\partial \dot{q}_{l}} \right) \end{aligned}~ \end{equation}

将求和拆分、计算偏导数并重新组合求和，得到：

\begin{equation} \begin{aligned} \frac{\partial T(\boldsymbol{q}, \boldsymbol{\dot{q}})}{\partial \dot{q}_{l}} &= \sum_{i \neq l}^{n} \sum_{j \neq l}^{n} \left( c_{ij}(\boldsymbol{q}) \frac{\partial \left[\dot{q}_{i} \dot{q}_{j}\right]}{\partial \dot{q}_{l}} \right) + \sum_{i \neq l}^{n} \left( c_{il}(\boldsymbol{q}) \frac{\partial \left[\dot{q}_{i} \dot{q}_{l}\right]}{\partial \dot{q}_{l}} \right) + \sum_{j \neq l}^{n} \left( c_{lj}(\boldsymbol{q}) \frac{\partial \left[\dot{q}_{l} \dot{q}_{j}\right]}{\partial \dot{q}_{l}} \right) + c_{ll}(\boldsymbol{q}) \frac{\partial \left[\dot{q}_{l}^{2}\right]}{\partial \dot{q}_{l}}\\ &= \sum_{i \neq l}^{n} \sum_{j \neq l}^{n} (0) + \sum_{i \neq l}^{n} \left( c_{il}(\boldsymbol{q}) \dot{q}_{i} \right) + \sum_{j \neq l}^{n} \left( c_{lj}(\boldsymbol{q}) \dot{q}_{j} \right) + 2c_{ll}(\boldsymbol{q}) \dot{q}_{l}\\ &= \sum_{i=1}^{n} \left( c_{il}(\boldsymbol{q}) \dot{q}_{i} \right) + \sum_{j=1}^{n} \left( c_{lj}(\boldsymbol{q}) \dot{q}_{j} \right) \end{aligned}~ \end{equation}

　　将上述结果乘以 \(\dot{q}_{l}\) 并对 \(l\) 求和，得到：

\begin{equation} \begin{aligned} \sum_{l=1}^{n} \left( \frac{\partial T(\boldsymbol{q}, \boldsymbol{\dot{q}})}{\partial \dot{q}_{l}} \dot{q}_{l} \right) &= \sum_{l=1}^{n} \left( \left( \sum_{i=1}^{n} \left( c_{il}(\boldsymbol{q}) \dot{q}_{i} \right) + \sum_{j=1}^{n} \left( c_{lj}(\boldsymbol{q}) \dot{q}_{j} \right) \right) \dot{q}_{l} \right)\\ &= \sum_{l=1}^{n} \sum_{i=1}^{n} \left( c_{il}(\boldsymbol{q}) \dot{q}_{i} \dot{q}_{l} \right) + \sum_{l=1}^{n} \sum_{j=1}^{n} \left( c_{lj}(\boldsymbol{q}) \dot{q}_{j} \dot{q}_{l} \right)\\ &= \sum_{i=1}^{n} \sum_{l=1}^{n} \left( c_{il}(\boldsymbol{q}) \dot{q}_{i} \dot{q}_{l} \right) + \sum_{l=1}^{n} \sum_{j=1}^{n} \left( c_{lj}(\boldsymbol{q}) \dot{q}_{l} \dot{q}_{j} \right)\\ &= T(\boldsymbol{q}, \boldsymbol{\dot{q}}) + T(\boldsymbol{q}, \boldsymbol{\dot{q}})\\ &= 2T(\boldsymbol{q}, \boldsymbol{\dot{q}}) \end{aligned}~ \end{equation}

这个简化是欧拉齐次函数定理的结果。

　　因此，哈密顿量变为

\begin{equation} \begin{aligned} {\mathcal {H}} &= \sum_{i=1}^{n} \left( \frac{\partial T(\boldsymbol{q}, \boldsymbol{\dot{q}})}{\partial \dot{q}_{i}} \dot{q}_{i} \right) - T(\boldsymbol{q}, \boldsymbol{\dot{q}}) + V(\boldsymbol{q}, t) \\ &= 2T(\boldsymbol{q}, \boldsymbol{\dot{q}}) - T(\boldsymbol{q}, \boldsymbol{\dot{q}}) + V(\boldsymbol{q}, t)\\ &= T(\boldsymbol{q}, \boldsymbol{\dot{q}}) + V(\boldsymbol{q}, t) \end{aligned}~ \end{equation}

在质点系统中的应用

　　对于质点系统，广义速度的平方项满足于 \( T(\mathbf{q}, \mathbf{\dot{q}}, t) = T(\mathbf{q}, \mathbf{\dot{q}}) \) 的情况，这也是 \( \mathcal{H} = T + V \) 成立的一个必要条件。

　　证明

　　考虑一个由 \( N \) 个点质量构成的系统的动能。如果假设 \( T(\boldsymbol{q}, \boldsymbol{\dot{q}}, t) = T(\boldsymbol{q}, \boldsymbol{\dot{q}}) \)，则可以证明 \( \dot{\mathbf{r}}_k(\boldsymbol{q}, \boldsymbol{\dot{q}}, t) = \dot{\mathbf{r}}_k(\boldsymbol{q}, \boldsymbol{\dot{q}}) \)（参见 Scleronomous 的应用部分）。因此，动能可以表示为

　　 \[ T(\boldsymbol{q}, \boldsymbol{\dot{q}}) = \frac{1}{2} \sum_{k=1}^{N} \left( m_k \dot{\mathbf{r}}_k(\boldsymbol{q}, \boldsymbol{\dot{q}}) \cdot \dot{\mathbf{r}}_k(\boldsymbol{q}, \boldsymbol{\dot{q}}) \right)~ \]

　　对于多变量的链式法则，可以用来展开速度：

\begin{equation} \begin{aligned} \dot{\mathbf{r}}_k(\boldsymbol{q}, \boldsymbol{\dot{q}}) &= \frac{d\mathbf{r}_k(\boldsymbol{q})}{dt}\\ &= \sum_{i=1}^{n} \left( \frac{\partial \mathbf{r}_k(\boldsymbol{q})}{\partial q_i} \dot{q}_i \right) \end{aligned}~ \end{equation}

结果为

\begin{equation} \begin{aligned} T(\boldsymbol{q}, \boldsymbol{\dot{q}}) &= \frac{1}{2} \sum_{k=1}^{N} \left( m_k \left( \sum_{i=1}^{n} \left( \frac{\partial \mathbf{r}_k(\boldsymbol{q})}{\partial q_i} \dot{q}_i \right) \cdot \sum_{j=1}^{n} \left( \frac{\partial \mathbf{r}_k(\boldsymbol{q})}{\partial q_j} \dot{q}_j \right) \right) \right)\\ &= \sum_{k=1}^{N} \sum_{i=1}^{n} \sum_{j=1}^{n} \left( \frac{1}{2} m_k \frac{\partial \mathbf{r}_k(\boldsymbol{q})}{\partial q_i} \cdot \frac{\partial \mathbf{r}_k(\boldsymbol{q})}{\partial q_j} \dot{q}_i \dot{q}_j \right)\\ &= \sum_{i=1}^{n} \sum_{j=1}^{n} \left( \sum_{k=1}^{N} \left( \frac{1}{2} m_k \frac{\partial \mathbf{r}_k(\boldsymbol{q})}{\partial q_i} \cdot \frac{\partial \mathbf{r}_k(\boldsymbol{q})}{\partial q_j} \right) \dot{q}_i \dot{q}_j \right)\\ &= \sum_{i=1}^{n} \sum_{j=1}^{n} \left( c_{ij}(\boldsymbol{q}) \dot{q}_i \dot{q}_j \right) \end{aligned}~ \end{equation}

此形式符合要求。

能量守恒

　　如果满足 \( \mathcal{H} = T + V \) 的条件，则哈密顿量的守恒意味着能量守恒。这要求额外满足条件，即势能 \( V \) 不包含时间作为显式变量。 \[ \frac{\partial V(\boldsymbol{q}, \boldsymbol{\dot{q}}, t)}{\partial t} = 0~ \] 在扩展的欧拉-拉格朗日方程形式下（参见拉格朗日力学 § 包含非保守力的扩展），瑞利耗散函数表示由于自然原因产生的能量耗散。因此，当 \( R \neq 0 \) 时，能量不再守恒。这与速度相关的势能相似。

　　总结而言，对于非相对论系统满足 \( \mathcal{H} = T + V = \text{时间常数} \) 的要求是：

\( V = V(\boldsymbol{q}) \)
\( T = T(\boldsymbol{q}, \boldsymbol{\dot{q}}) \)
\( T \) 是 \( \boldsymbol{\dot{q}} \) 的齐次二次函数。

5. 带电粒子在电磁场中的哈密顿量

　　带电粒子在电磁场中的哈密顿力学的一个足够的例子是带电粒子的哈密顿量。在笛卡尔坐标系下，非相对论经典粒子在电磁场中的拉格朗日函数（采用 SI 单位）为： \[ \mathcal{L} = \sum_{i} \frac{1}{2} m \dot{x}_i^2 + \sum_{i} q \dot{x}_i A_i - q \varphi,~ \] 其中 \( q \) 是粒子的电荷，\( \varphi \) 是电标势，而 \( A_i \) 是磁矢势的分量，可能显式地依赖于 \( x_i \) 和 \( t \)。

　　该拉格朗日函数结合欧拉-拉格朗日方程得出洛伦兹力定律： \[ m \ddot{\mathbf{x}} = q \mathbf{E} + q \dot{\mathbf{x}} \times \mathbf{B} ~, \] 被称为最小耦合。

　　正则动量由以下公式给出： \[ p_i = \frac{\partial \mathcal{L}}{\partial \dot{x}_i} = m \dot{x}_i + q A_i.~ \] 哈密顿量作为拉格朗日函数的勒让德变换，因此为： \[ \mathcal{H} = \sum_{i} \dot{x}_i p_i - \mathcal{L} = \sum_{i} \frac{\left( p_i - q A_i \right)^2}{2m} + q \varphi.~ \] 该方程在量子力学中经常使用。

　　在规范变换下： \[ \mathbf{A} \rightarrow \mathbf{A} + \nabla f \,, \quad \varphi \rightarrow \varphi - \dot{f},~ \] 其中 \( f(\mathbf{r}, t) \) 是空间和时间的任意标量函数。上述的拉格朗日函数、正则动量和哈密顿量变换如下： \[ L \rightarrow L' = L + q \frac{df}{dt} \,, \quad \mathbf{p} \rightarrow \mathbf{p}' = \mathbf{p} + q \nabla f \,, \quad H \rightarrow H' = H - q \frac{\partial f}{\partial t} ,~ \] 这仍然会产生相同的哈密顿方程：

\begin{equation} \begin{aligned} \left. \frac{\partial H'}{\partial {x_i}} \right|_{p'_i} &= \left. \frac{\partial}{\partial {x_i}} \right|_{p'_i} ({\dot{x}}_i p'_i - L') = - \left. \frac{\partial L'}{\partial {x_i}} \right|_{p'_i}\\ &= - \left. \frac{\partial L}{\partial {x_i}} \right|_{p'_i} - q \left. \frac{\partial}{\partial {x_i}} \right|_{p'_i} \frac{df}{dt} \\ &= - \frac{d}{dt} \left( \left. \frac{\partial L}{\partial {\dot{x}_i}} \right|_{p'_i} + q \left. \frac{\partial f}{\partial {x_i}} \right|_{p'_i} \right)\\ &= - \dot{p}'_i \end{aligned}~ \end{equation}

　　在量子力学中，波函数在规范变换过程中也会经历一个局部 \( U(1) \) 群变换，这意味着所有物理结果必须在局部 \( U(1) \) 变换下保持不变。

在电磁场中的相对论性带电粒子

　　带电粒子（静止质量为 \( m \)，电荷为 \( q \)）的相对论拉格朗日函数为： \[ \mathcal{L}(t) = -mc^2 \sqrt{1 - \frac{\dot{\mathbf{x}}(t)^2}{c^2}} + q \dot{\mathbf{x}}(t) \cdot \mathbf{A}(\mathbf{x}(t), t) - q \varphi(\mathbf{x}(t), t)~ \] 因此，粒子的正则动量为 \[ \mathbf{p}(t) = \frac{\partial \mathcal{L}}{\partial \dot{\mathbf{x}}} = \frac{m \dot{\mathbf{x}}}{\sqrt{1 - \frac{\dot{\mathbf{x}}^2}{c^2}}} + q \mathbf{A}~ \] 也就是说，它是动量和势动量的总和。

　　求解速度，得到 \[ \dot{\mathbf{x}}(t) = \frac{\mathbf{p} - q \mathbf{A}}{\sqrt{m^2 + \frac{1}{c^2} (\mathbf{p} - q \mathbf{A})^2}}~ \] 因此，哈密顿量为 \[ \mathcal{H}(t) = \dot{\mathbf{x}} \cdot \mathbf{p} - \mathcal{L} = c \sqrt{m^2 c^2 + (\mathbf{p} - q \mathbf{A})^2} + q \varphi~ \] 这导致力方程（等同于欧拉-拉格朗日方程） \[ \dot{\mathbf{p}} = -\frac{\partial \mathcal{H}}{\partial \mathbf{x}} = q \dot{\mathbf{x}} \cdot (\nabla \mathbf{A}) - q \nabla \varphi = q \nabla (\dot{\mathbf{x}} \cdot \mathbf{A}) - q \nabla \varphi~ \] 由此可以推导出

\begin{equation} \begin{aligned} \frac{d}{dt} \left( \frac{m \dot{\mathbf{x}}}{\sqrt{1 - \frac{\dot{\mathbf{x}}^2}{c^2}}} \right) &= \frac{d}{dt} (\mathbf{p} - q \mathbf{A}) = \dot{\mathbf{p}} - q \frac{\partial \mathbf{A}}{\partial t} - q (\dot{\mathbf{x}} \cdot \nabla) \mathbf{A}\\ &= q \nabla (\dot{\mathbf{x}} \cdot \mathbf{A}) - q \nabla \varphi - q \frac{\partial \mathbf{A}}{\partial t} - q (\dot{\mathbf{x}} \cdot \nabla) \mathbf{A}\\ &= q \mathbf{E} + q \dot{\mathbf{x}} \times \mathbf{B} \end{aligned}~ \end{equation}

　　上述推导使用了矢量运算的恒等式： \[ \frac{1}{2} \nabla (\mathbf{A} \cdot \mathbf{A}) = \mathbf{A} \cdot \mathbf{J}_{\mathbf{A}} = \mathbf{A} \cdot (\nabla \mathbf{A}) = (\mathbf{A} \cdot \nabla) \mathbf{A} + \mathbf{A} \times (\nabla \times \mathbf{A}).~ \] 哈密顿量的等价表达式（作为相对论动量 \( \mathbf{P} = \gamma m \dot{\mathbf{x}}(t) = \mathbf{p} - q \mathbf{A} \) 的函数）为： \[ \mathcal{H}(t) = \dot{\mathbf{x}}(t) \cdot \mathbf{P}(t) + \frac{mc^2}{\gamma} + q \varphi(\mathbf{x}(t), t) = \gamma mc^2 + q \varphi(\mathbf{x}(t), t) = E + V~ \] 这样表达的优势在于动量 \( \mathbf{P} \) 可以通过实验测量，而正则动量 \( \mathbf{p} \) 则不能。请注意，哈密顿量（总能量）可以视为相对论能量（动能+静能）\( E = \gamma mc^2 \) 与势能 \( V = q \varphi \) 的总和。

6. 从辛几何到哈密顿方程

哈密顿系统的几何结构

　　哈密顿量可以在一个光滑的偶数维流形 \( M_{2n} \) 上诱导出一种辛结构，有几种等价的方法，最著名的如下：

　　作为一个闭合的非退化辛 2-形式 \( \omega \)。根据达布定理，在流形 \( M \) 上的任意一点的一个小邻域内，存在适当的局部坐标 \( p_{1}, \cdots, p_{n}, q_{1}, \cdots, q_{n} \)（正则坐标或辛坐标），使得辛形式变为： \[ \omega = \sum_{i=1}^{n} dp_{i} \wedge dq_{i} \,.~ \] 形式 \( \omega \) 诱导了切空间与余切空间的自然同构：\( T_x M \cong T_x^* M \)。这是通过将一个向量 \( \xi \in T_x M \) 映射到一个 1-形式 \( \omega_\xi \in T_x^* M \)，其中对所有 \( \eta \in T_x M \)，有 \( \omega_\xi(\eta) = \omega(\eta, \xi) \)。由于 \( \omega \) 的双线性和非退化性以及 \( \dim T_x M = \dim T_x^* M \)，映射 \( \xi \to \omega_\xi \) 确实是一个线性同构。这个同构是自然的，即它在 \( M \) 上的坐标变换下不变。对于所有 \( x \in M \)，重复这一过程，我们得到一个从平滑向量场空间到平滑 1-形式空间的同构 \( J^{-1}: \text{Vect}(M) \to \Omega^1(M) \)。对于任意 \( f, g \in C^{\infty}(M, \mathbb{R}) \) 和 \( \xi, \eta \in \text{Vect}(M) \)， \[ J^{-1}(f \xi + g \eta) = f J^{-1}(\xi) + g J^{-1}(\eta).~ \] （用代数术语来说，这表明 \( C^{\infty}(M, \mathbb{R}) \)-模 \( \text{Vect}(M) \) 和 \( \Omega^1(M) \) 是同构的。）如果 \( H \in C^{\infty}(M \times \mathbb{R}_t, \mathbb{R}) \)，则对任意固定的 \( t \in \mathbb{R}_t \)，有 \( dH \in \Omega^1(M) \)，且 \( J(dH) \in \text{Vect}(M) \)。\( J(dH) \) 称为哈密顿向量场。对应的微分方程 \[ \dot{x} = J(dH)(x)~ \] 称为哈密顿方程。这里 \( x = x(t) \)，\( J(dH)(x) \in T_x M \) 是在 \( x \in M \) 处向量场 \( J(dH) \) 的（时间相关的）值。

　　哈密顿系统可以理解为一个时间 \( \mathbb{R} \) 上的纤维丛 \( E \)，其中纤维 \( E_t \) 是在时间 \( t \in \mathbb{R} \) 处的位置空间。因此，拉格朗日函数是定义在 \( E \) 上的射丛 \( J \) 上的一个函数；对拉格朗日函数进行纤维方向的勒让德变换生成一个时间上的对偶丛上的函数，其在 \( t \) 处的纤维是余切空间 \( T^* E_t \)，配备了一个自然的辛形式，这后一函数即为哈密顿量。拉格朗日力学和哈密顿力学之间的对应关系通过自明的 1-形式实现。

　　任何在辛流形上的光滑实值函数 \( H \) 都可以用于定义一个哈密顿系统。该函数 \( H \) 称为 “哈密顿量” 或 “能量函数”。此时，辛流形称为相空间。哈密顿量在辛流形上诱导一个特殊的向量场，称为哈密顿向量场。

　　哈密顿向量场在流形上诱导一个哈密顿流。这是一个关于流形的单参数变换族（曲线的参数通常称为 “时间”）；换句话说，它是以恒等变换为起点的一个辛同胚的同伦。根据刘维尔定理，每个辛同胚保持相空间上的体积形式。由哈密顿流诱导的这些辛同胚的集合通常称为哈密顿系统的 “哈密顿力学”。

　　辛结构诱导了一个泊松括号。泊松括号赋予流形上函数空间一个李代数的结构。

　　如果 \( F \) 和 \( G \) 是 \( M \) 上的光滑函数，那么光滑函数 \( \omega(J(dF), J(dG)) \) 被适当地定义为函数 \( F \) 和 \( G \) 的泊松括号，记作 \( \{F, G\} \)。泊松括号具有以下性质：

双线性
反对称性
莱布尼兹规则：\(\{F_1 \cdot F_2, G\} = F_1 \{F_2, G\} + F_2 \{F_1, G\}\)
雅可比恒等式：\(\{\{H, F\}, G\} + \{\{F, G\}, H\} + \{\{G, H\}, F\} \equiv 0\)
非退化性：如果 \( M \) 上的点 \( x \) 对 \( F \) 不是临界点，则存在一个光滑函数 \( G \)，使得 \( \{F, G\}(x) \neq 0 \)。

　　给定一个函数 \( f \)， \[ \frac{d}{dt} f = \frac{\partial}{\partial t} f + \{f, \mathcal{H}\},~ \] 如果存在一个概率分布 \( \rho \)，那么（由于相空间速度 \( (\dot{p}_i, \dot{q}_i) \) 的散度为零且概率守恒），其对流导数可以证明为零，因此 \[ \frac{\partial}{\partial t} \rho = -\{\rho, \mathcal{H}\}~ \] 这被称为刘维尔定理。辛流形上的每一个光滑函数 \( G \) 都生成一个单参数辛同胚族，如果 \( \{G, H\} = 0 \)，则 \( G \) 是守恒的，这些辛同胚是对称变换。

　　一个哈密顿量可能具有多个守恒量 \( G_i \)。如果辛流形的维数为 \( 2n \)，且存在 \( n \) 个函数独立且彼此交换的守恒量 \( G_i \)（即 \( \{G_i, G_j\} = 0 \)），则该哈密顿量是刘维尔可积的。刘维尔-阿诺德定理指出，局部上，任何刘维尔可积的哈密顿量可以通过一个辛同胚变换为一个新的哈密顿量，其中守恒量 \( G_i \) 成为坐标；这些新坐标称为作用–角坐标。变换后的哈密顿量仅依赖于 \( G_i \)，因此运动方程形式简化为 \[ \dot{G}_i = 0, \quad \dot{\varphi}_i = F_i(G)~ \] 对于某些函数 \( F \)【9】。有一个完整的研究领域专注于由 KAM 定理描述的可积系统的微小偏离。

　　哈密顿向量场的可积性是一个未解决的问题。一般而言，哈密顿系统是混沌的；测度、完备性、可积性和稳定性的概念定义不明确。

黎曼流形

　　一个重要的特例是二次型的哈密顿量，即可以表示为 \[ \mathcal{H}(q, p) = \frac{1}{2} \langle p, p \rangle_q~ \] 其中 \( \langle , \rangle_q \) 是纤维 \( T^*_q Q \) 上平滑变化的内积，即构型空间中点 \( q \) 的余切空间，有时称为共度量。这种哈密顿量完全由动能项组成。

　　如果考虑一个黎曼流形或伪黎曼流形，黎曼度量在切丛和余切丛之间引入了一个线性同构。（参见 Musical isomorphism）。利用这个同构，可以定义一个共度量。（在坐标中，定义共度量的矩阵是定义度量的矩阵的逆矩阵。）这种哈密顿量的哈密顿-雅可比方程的解与流形上的测地线相同。特别地，在这种情况下，哈密顿流就是测地流。有关此类解的存在性及其解集的完备性，在测地线上有详细讨论。另请参见测地线作为哈密顿流。

次黎曼流形

　　当共度量是退化的时，它不可逆。在这种情况下，由于没有度量，便没有黎曼流形。然而，哈密顿量仍然存在。如果在构型空间流形 \( Q \) 的每个点 \( q \) 上共度量都是退化的，使得共度量的秩小于流形 \( Q \) 的维数，则称其为次黎曼流形。

　　在这种情况下的哈密顿量称为次黎曼哈密顿量。每个这样的哈密顿量唯一地决定了共度量，反之亦然。这意味着每个次黎曼流形都由其次黎曼哈密顿量唯一确定，反之亦然：每个次黎曼流形都有一个唯一的次黎曼哈密顿量。根据 Chow–Rashevskii 定理，次黎曼测地线的存在性得以保证。

　　连续实值的海森堡群提供了一个次黎曼流形的简单例子。对于海森堡群，哈密顿量为 \[ \mathcal{H}(x, y, z, p_x, p_y, p_z) = \frac{1}{2} (p_x^2 + p_y^2).~ \] 其中 \( p_z \) 不参与哈密顿量。

泊松代数

　　哈密顿系统可以通过多种方式进行推广。除了仅仅研究辛流形上的光滑函数代数外，哈密顿力学还可以在一般的交换幺半实泊松代数上进行表述。一个状态是泊松代数上的一个连续线性泛函（配备适当的拓扑），使得对于代数中的任意元素 \( A \)，\( A^2 \) 映射到一个非负实数。

　　进一步的推广是南部动力学。

通过泊松括号向量子力学的推广

　　以上的哈密顿方程在经典力学中运作良好，但在量子力学中却不适用，因为这些微分方程假设可以在任意时刻同时精确地指定粒子的位置和动量。然而，这些方程可以进一步推广，使其不仅适用于经典力学，还适用于量子力学，通过将 \( p \) 和 \( q \) 上的泊松代数变形为莫 oyal 括号代数来实现。

　　更一般形式的哈密顿方程为 \[ \frac{d f}{d t} = \{f, \mathcal{H}\} + \frac{\partial f}{\partial t},~ \] 其中 \( f \) 是 \( p \) 和 \( q \) 的某个函数，\( H \) 是哈密顿量。要了解评估泊松括号的规则而不借助微分方程，请参见李代数；泊松括号是泊松代数中的李括号的名称。然后可以将这些泊松括号扩展为与非等价李代数相符合的莫 oyal 括号，这一点由 Hilbrand J. Groenewold 证明，从而描述相空间中的量子力学扩散（参见相空间表述和 Wigner–Weyl 变换）。这种更代数化的方法不仅最终允许将相空间中的概率分布扩展到 Wigner 准概率分布，而且在纯泊松括号的经典设置中，也更有助于分析系统中的相关守恒量。

7. 另见

正则变换
经典场论
哈密顿场论
哈密顿光学-力学类比
协变哈密顿场论
经典力学
动力系统理论
哈密顿系统
哈密顿-雅可比方程
哈密顿-雅可比-爱因斯坦方程
拉格朗日力学
麦克斯韦方程
哈密顿量（量子力学）
量子哈密顿方程
量子场论
哈密顿光学
De Donder–Weyl 理论
几何力学
Routhian 力学
南部力学
哈密顿流体力学
哈密顿向量场

8. 参考文献

Hamilton, William Rowan, Sir (1833). *On a general method of expressing the paths of light, & of the planets, by the coefficients of a characteristic function.* Printed by P.D. Hardy. OCLC 68159539.
Landau & Lifshitz 1976, 第 33–34 页
该推导参考了 Arnol'd 1989, 第 65–66 页
Goldstein, Poole & Safko 2002, 第 347–349 页
Malham 2016, 第 49–50 页
Landau & Lifshitz 1976, 第 14 页
Zinn-Justin, Jean; Guida, Riccardo (2008-12-04). "Gauge invariance". Scholarpedia. 3 (12): 8287. Bibcode:2008SchpJ...3.8287Z. doi:10.4249/scholarpedia.8287. ISSN 1941-6016.
Arnol'd, Kozlov & Neĩshtadt 1988, §3. Hamiltonian mechanics.
Arnol'd, Kozlov & Neĩshtadt 1988.

9. 延伸阅读

Landau, Lev Davidovich；Lifshitz, Evgenii Mikhailovich（1976）。*力学*。《理论物理学教程》。第 1 卷。Sykes, J. B.（John Bradbury），Bell, J. S.（第 3 版）。牛津。ISBN 0-08-021022-8。OCLC 2591126。
Abraham, R.; Marsden, J.E.（1978）。*力学的基础*（第 2 版，修订、扩展版）。马萨诸塞州雷丁：Benjamin/Cummings 出版社。ISBN 0-8053-0102-X。OCLC 3516353。
Arnol'd, V. I.; Kozlov, V. V.; Neĩshtadt, A. I.（1988）。*经典力学和天体力学的数学方面*。《数学科学百科全书》，动力系统 III。第 3 卷。Anosov, D. V. 主编。柏林：Springer-Verlag。ISBN 0-387-17002-2。OCLC 16404140。
Arnol'd, V. I.（1989）。*经典力学的数学方法*（第 2 版）。纽约：Springer-Verlag。ISBN 0-387-96890-3。OCLC 18681352。
Goldstein, Herbert；Poole, Charles P. Jr.；Safko, John L.（2002）。*经典力学*（第 3 版）。旧金山：Addison Wesley。ISBN 0-201-31611-0。OCLC 47056311。
Vinogradov, A. M.; Kupershmidt, B. A.（1977 年 8 月 31 日）。《哈密顿力学的结构》。*俄罗斯数学概览*。32 (4): 177–243。Bibcode: 1977RuMaS..32..177V。doi:10.1070/RM1977v032n04ABEH001642。ISSN 0036-0279。S2CID 250805957。