开普勒定律(综述)
贡献者: 待更新
本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章。
在天文学中,开普勒的行星运动定律由约翰内斯·开普勒于 1609 年发布(除了第三定律,后者于 1619 年完全发布),描述了行星围绕太阳的轨道。这些定律用椭圆轨道代替了哥白尼日心说中的圆形轨道和本轮,并解释了行星速度的变化。这三条定律如下:
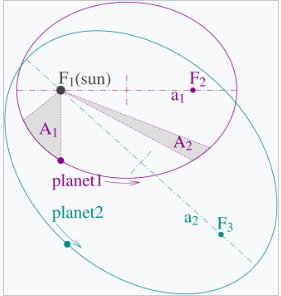
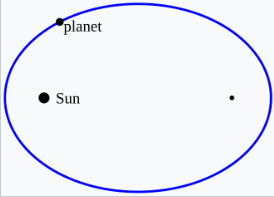
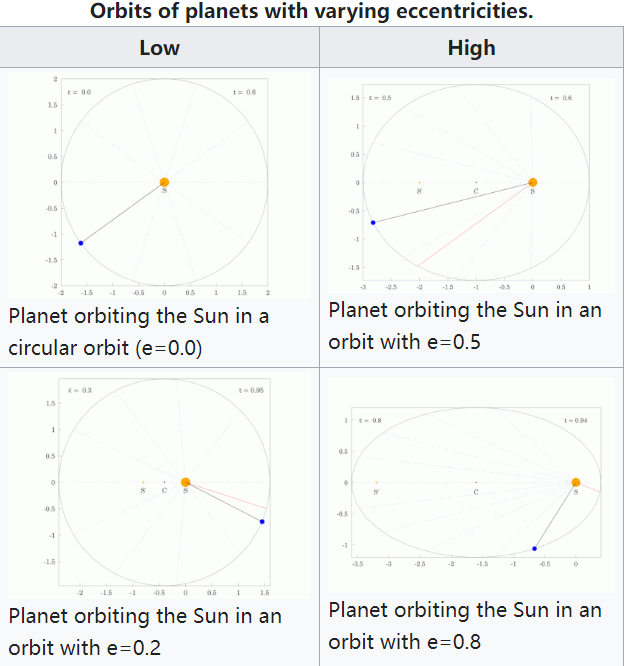
- 行星的轨道是椭圆,太阳位于其中一个焦点上。
- 连接行星和太阳的线段在相等的时间间隔内扫过相等的面积。
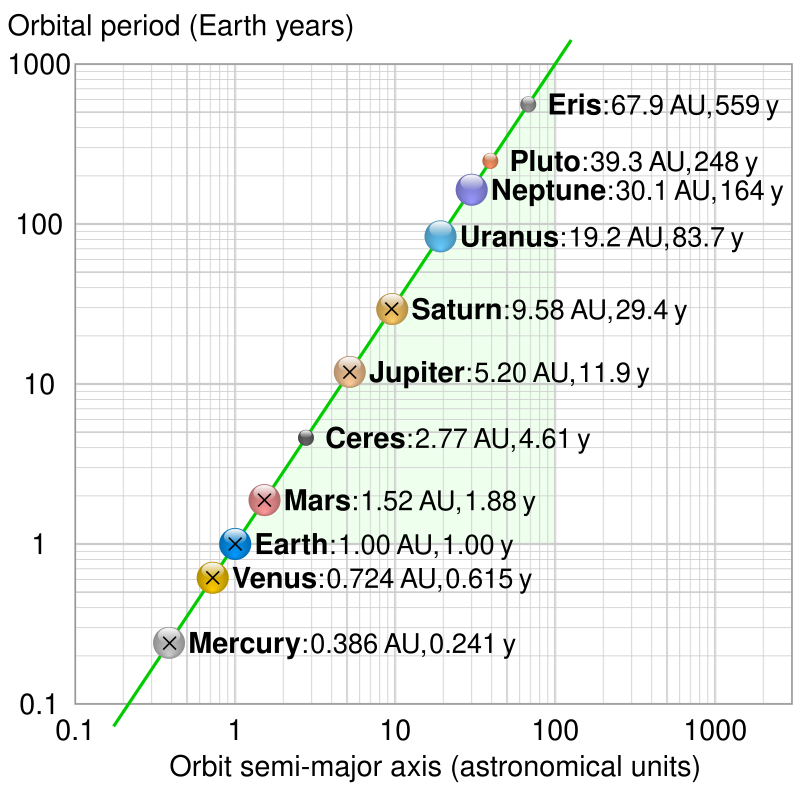
- 行星轨道周期的平方与其轨道半长轴的立方成正比。
行星的椭圆轨道通过火星轨道的计算得到了证明。从这些计算中,开普勒推断出太阳系中其他天体(包括距离太阳较远的天体)也具有椭圆轨道。第二定律确定了当行星靠近太阳时,其运动速度较快。第三定律表达了行星距离太阳越远,其轨道周期越长。
艾萨克·牛顿在 1687 年证明,像开普勒定律这样的关系,作为他自己运动定律和万有引力定律的结果,也适用于太阳系。
更精确的历史方法可以在《新天文学》和《哥白尼天文学概要》中找到。
1. 与哥白尼的比较
约翰内斯·开普勒的定律改进了哥白尼的模型。根据哥白尼的观点:
- 行星轨道是一个带有本轮的圆形。
- 太阳大致位于轨道的中心。
- 行星在主轨道中的速度是恒定的。
尽管哥白尼正确地指出了行星绕太阳转,但他在定义行星轨道时是错误的。开普勒通过引入超越几何的物理解释,正确地定义了行星轨道,如下所示:
- 行星轨道不是带有本轮的圆形,而是椭圆形。
- 太阳不在轨道的中心,而是在椭圆轨道的一个焦点上。
- 行星在轨道中的线速度和角速度都不是恒定的,但面积速度(与角动量的概念密切相关)是恒定的。
地球轨道的离心率使得从 3 月春分到 9 月秋分的时间约为 186 天,不等于从 9 月秋分到 3 月春分的时间约为 179 天。如果用一条直径将轨道分成两部分,轨道将被平分,但通过太阳的平面与地球赤道平行的平面将轨道分成两部分,面积比约为 186 比 179。因此,地球轨道的离心率约为: \[ e \approx \frac{\pi}{4} \cdot \frac{186-179}{186+179} \approx 0.015~ \] 这个值接近正确值(0.016710218)。这个计算的准确性要求选择的两个日期位于椭圆轨道的短轴上,并且每一半的中点位于长轴上。由于这里选择的日期是春分和秋分,这个计算在近日点(地球最接近太阳的日期)恰好落在冬至时是正确的。目前的近日点,接近 1 月 4 日,比较接近 12 月 21 日或 22 日的冬至。
2. 命名法
开普勒工作的当前表述形式花了近两个世纪才定型。伏尔泰的《牛顿哲学要义》(*Eléments de la philosophie de Newton*,1738 年)是第一部使用 “定律” 术语的出版物。[6][7] 《天文学家传记百科全书》在关于开普勒的条目中(第 620 页)指出,至少从约瑟夫·德·拉兰德(Joseph de Lalande)时代起,科学定律的术语就已被使用。[8] 是罗伯特·斯莫尔(Robert Small)在其 1814 年出版的《开普勒的天文发现概述》(*An Account of the Astronomical Discoveries of Kepler*)中,将这三条定律定型,加入了第三条。[9] 斯莫尔还声称(与历史记载不符),这些定律是基于归纳推理的经验定律。[7][10]
此外,目前使用的 “开普勒第二定律” 其实是一个误称。开普勒有两个版本的定律,在定性上有所关联:“距离定律” 和 “面积定律”。“面积定律” 最终成为三条定律中的第二条;但开普勒自己并没有以这种方式优先考虑它。[11]
3. 历史
开普勒于 1609 年发布了他的前两条行星运动定律,[12] 这些定律是通过分析第谷·布拉赫的天文观测数据发现的。[13][14][15][5]: 53 开普勒的第三定律则在 1619 年发布。[16][14] 开普勒信仰哥白尼的太阳系模型,该模型要求行星沿圆形轨道运行,但他无法将布拉赫非常精确的观测数据与火星轨道的圆形拟合起来——火星的离心率恰好是除水星之外所有行星中最高的。[17] 他的第一定律反映了这一发现。
在 1621 年,开普勒注意到他的第三定律也适用于木星的四颗最亮的卫星。[Nb 1] 戈德弗罗伊·温德林(Godefroy Wendelin)也在 1643 年做出了这一观察。[Nb 2] 第二定律(以 “面积定律” 形式)在 1664 年由尼古拉斯·梅尔卡托尔(Nicolaus Mercator)在一本书中提出异议,但到了 1670 年,他的《哲学汇刊》已支持这一理论。[18][19] 随着世纪的推进,这一理论变得更加广泛接受。[20] 德国的接受情况在 1688 年(牛顿的《原理》出版并被视为基本的哥白尼主义作品)和 1690 年(戈特弗里德·莱布尼茨关于开普勒工作的成果出版)之间发生了显著变化。[21]
牛顿被认为理解了第二定律并非仅适用于万有引力的平方反比定律,而是仅作为该定律径向性质的结果,而其他定律则依赖于吸引力的平方反比形式。卡尔·龙格(Carl Runge)和威廉·伦茨(Wilhelm Lenz)在很晚时候在行星运动的相空间中识别出一个对称性原理(正交群 O(4) 的作用),该原理解释了牛顿引力下的第一和第三定律,类似于角动量的守恒通过旋转对称性解释第二定律。[22]
4. 公式
行星在开普勒定律作用下的运动学数学模型允许进行大量进一步的计算。
第一定律
开普勒的第一定律指出:
每颗行星的轨道是椭圆形的,太阳位于椭圆的两个焦点之一。
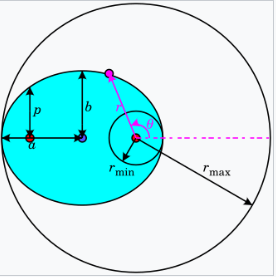
一个椭圆可以用以下公式表示: \[ r = \frac{p}{1 + \varepsilon \cos \theta}~ \] 其中:\( p \) 是半准线,\( \varepsilon \) 是椭圆的离心率,\( r \) 是从太阳到行星的距离,\( \theta \) 是从太阳看行星当前位置到其最近点的角度。所以 \( (r, \theta) \) 是极坐标。
对于椭圆,\( 0 < \varepsilon < 1 \);在极限情况下,当 \( \varepsilon = 0 \) 时,轨道是一个圆形,太阳位于中心(即零离心率的情况)。
当 \( \theta = 0^\circ \) 时,近日点,距离最小: \[ r_{\min} = \frac{p}{1 + \varepsilon}~ \] 当 \( \theta = 90^\circ \) 和 \( \theta = 270^\circ \) 时,距离等于 \( p \)。 当 \( \theta = 180^\circ \) 时,远日点,距离最大(根据定义,远日点永远是近日点加 180°): \[ r_{\max} = \frac{p}{1 - \varepsilon}~ \] 半长轴 \( a \) 是 \( r_{\min} \) 和 \( r_{\max} \) 的算术平均值: \[ a = \frac{r_{\max} + r_{\min}}{2}~ \] \[ a = \frac{p}{1 - \varepsilon^2}~ \] 半短轴 \( b \) 是 \( r_{\min} \) 和 \( r_{\max} \) 的几何平均值: \[ b = \sqrt{r_{\max} r_{\min}}~ \] \[ b = \frac{p}{\sqrt{1 - \varepsilon^2}}~ \] 半准线 \( p \) 是 \( r_{\min} \) 和 \( r_{\max} \) 的调和平均值: \[ p = \left( \frac{r_{\max}^{-1} + r_{\min}^{-1}}{2} \right)^{-1}~ \] \[pa = r_{\max} r_{\min} = b^2~\] 离心率 \( \varepsilon \) 是 \( r_{\min} \) 和 \( r_{\max} \) 之间的变异系数: \[ \varepsilon = \frac{r_{\max} - r_{\min}}{r_{\max} + r_{\min}}~ \] 椭圆的面积是: \[ A = \pi ab~ \] 圆的特殊情况是 \( \varepsilon = 0 \),此时 \( r = p = r_{\min} = r_{\max} = a = b \),并且 \( A = \pi r^2 \)。
第二定律
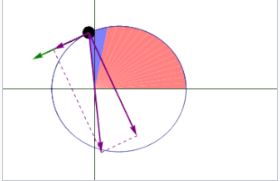
开普勒的第二定律指出:
连接行星和太阳的直线在相等时间间隔内扫过相等的面积。[23]
行星在椭圆轨道上的轨道半径和角速度会发生变化。这在动画中有所展示:当行星靠近太阳时,它的速度较快;而当行星远离太阳时,速度较慢。开普勒的第二定律指出,蓝色扇形区域的面积是恒定的。
历史与证明
开普勒显著地通过一些假设得出了这一定律,这些假设要么只是近似正确,要么是完全错误的,可以概括如下:
- 行星是通过太阳的某种力被推动绕太阳运行的。这个错误的假设依赖于错误的亚里士多德物理学,即物体需要不断被推动才能维持运动。
- 太阳的推动力与太阳的距离成反比。开普勒基于这种推理,认为引力应该是三维空间扩展的,而不是平面上的浪费。因此,他提出了一个反比定律,而不是[正确的]平方反比定律。
- 由于开普勒认为力与速度成正比,因此从第 1 条和第 2 条假设中可以推导出,速度与距离成反比。这也是亚里士多德物理学中的错误观念。
- 由于速度与时间成反比,因此从太阳的距离将与绕轨道小段的时间成正比。这对于椭圆轨道大致是正确的。
- 扫过的面积与整体时间成正比。这也大致是正确的。
- 行星的轨道是圆形的(开普勒在提出第二定律之前就发现了这一点,这与此相矛盾)。
然而,第二定律的结果是完全正确的,因为它在逻辑上等价于角动量的守恒,这对于任何受到径向对称力作用的物体都成立。[24] 可以通过以下证明来展示这一点。由于两个向量的叉积给出了这两个向量构成的平行四边形的面积,因此在短时间内扫过的三角形面积 \( dA \) 可以通过 \( \vec{r} \) 和 \( \vec{dx} \) 向量的叉积的一半来表示,其中 \( dx \) 是轨道的小段。 \[ dA = \frac{1}{2} (\vec{r} \times \vec{dx}) = \frac{1}{2} (\vec{r} \times \vec{v} dt)~ \] 其中 \( dx \) 是轨道的小段,\( dt \) 是覆盖该段所需的时间。
因此, \[ \frac{dA}{dt} = \frac{1}{2} (\vec{r} \times \vec{v})~ \] \[ \frac{dA}{dt} = \frac{1}{m} \frac{1}{2} (\vec{r} \times \vec{p})~ \] 由于最终的表达式与总角动量 \( (\vec{r} \times \vec{p}) \) 成正比,开普勒的等面积定律将适用于任何守恒角动量的系统。由于任何径向力都不会对行星的运动产生力矩,角动量将得到守恒。
关于椭圆参数
在一个很短的时间 \( dt \) 内,行星扫过一个小三角形,底边为 \( r \),高为 \( r \, d\theta \),其面积为: \[ dA = \frac{1}{2} \cdot r \cdot r \, d\theta~ \] 因此,恒定的面积速度为: \[ \frac{dA}{dt} = \frac{r^{2}}{2} \frac{d\theta}{dt}~ \] 椭圆轨道所围成的面积为 \( \pi ab \),因此周期 \( T \) 满足: \[ T \cdot \frac{r^{2}}{2} \frac{d\theta}{dt} = \pi ab~ \] 行星围绕太阳的平均运动 \( n \) 满足: \[ n = \frac{2\pi}{T}~ \] 于是有: \[ r^{2} d\theta = abn \, dt~ \] 因此: \[ \frac{dA}{dt} = \frac{abn}{2} = \frac{\pi ab}{T}~ \]
第三定律
开普勒的第三定律表述为:
任何绕同一主星运行的物体,其轨道周期的平方与轨道半长轴的立方之比是相同的。
这一规律揭示了行星与太阳的距离以及它们的轨道周期之间的关系。
开普勒在 1619 年表述了这一第三定律,他艰难地尝试通过精确的规律确定他所认为的 “天体的音乐”,并以音乐符号的形式表达出来[25]。因此,它也被称为**谐波定律**[26]。这一定律的最初形式(提到的不是半长轴,而是 “平均距离”)仅适用于偏心率接近零的行星[27]。
利用牛顿的引力定律(1687 年发布),在圆形轨道的情况下,我们可以通过将向心力与引力相等来得到这一关系: \[ mr\omega^2 = G\frac{mM}{r^2}~ \] 接着,将角速度 \(\omega\) 表达为轨道周期 \(T\) 的形式,并进行重排,最终得到开普勒的第三定律: \[ mr\left(\frac{2\pi}{T}\right)^2 = G\frac{mM}{r^2} \implies T^2 = \left(\frac{4\pi^2}{GM}\right)r^3 \implies T^2 \propto r^3~ \] 通过更详细的推导,可以得到一般椭圆轨道的情况,而不仅仅是圆形轨道,并且考虑绕质心(而不仅仅是大质量物体)运动。这将导致将圆半径 \(r\) 替换为椭圆运动中的半长轴 \(a\),同时将大质量 \(M\) 替换为 \(M+m\)。然而,由于行星的质量远小于太阳质量,这个修正通常被忽略。完整的公式是: \[ \frac{a^3}{T^2} = \frac{G(M+m)}{4\pi^2} \approx \frac{GM}{4\pi^2} \approx 7.496 \times 10^{-6} \frac{\text{AU}^3}{\text{days}^2} \text{是常数}~ \] 其中,\(M\) 是太阳的质量,\(m\) 是行星的质量,\(G\) 是引力常数,\(T\) 是轨道周期,\(a\) 是椭圆的半长轴,AU 是天文单位,即地球与太阳的平均距离。
表格
下表显示了开普勒用来经验性地推导他的定律的数据:
| 行星 | 到太阳的平均距离(AU) | 周期(天) | \({\frac {R^{3}}{T^{2}}}\) (10⁻⁶ AU³/天²) |
| 水星 | 0.389 | 87.77 | 7.64 |
| 金星 | 0.724 | 224.70 | 7.52 |
| 地球 | 1 | 365.25 | 7.50 |
| 火星 | 1.524 | 686.95 | 7.50 |
| 木星 | 5.20 | 4332.62 | 7.49 |
| 土星 | 9.510 | 10759.2 | 7.43 |
开普勒在发现这个规律之前,意识到约翰·纳皮尔最近发明了对数和对数-对数图。[28]
在发现这个规律后,开普勒写道:[29]
我一开始以为我在做梦……但可以完全肯定并准确地说,任何两颗行星之间的周期时间比,正是它们平均距离的 3/2 次方的比值。
—— 摘自《世界和谐》中的开普勒(1619 年)
作为比较,以下是现代的估计值:
| 行星 | 半长轴(AU) | 周期(天) | \({\frac {a^{3}}{T^{2}}}\) (10⁻⁶ AU³/天²) |
| 水星 | 0.38710 | 87.9693 | 7.496 |
| 金星 | 0.72333 | 224.7008 | 7.496 |
| 地球 | 1 | 365.2564 | 7.496 |
| 火星 | 1.52366 | 686.9796 | 7.495 |
| 木星 | 5.20336 | 4332.8201 | 7.504 |
| 土星 | 9.53707 | 10775.599 | 7.498 |
| 天王星 | 19.1913 | 30687.153 | 7.506 |
| 海王星 | 30.0690 | 60190.03 | 7.504 |
5. 行星加速度
艾萨克·牛顿在《自然哲学的数学原理》中计算了根据开普勒的第一定律和第二定律运动的行星的加速度。
- 加速度的方向指向太阳。
- 加速度的大小与行星到太阳的距离的平方成反比(平方反比定律)。
这意味着太阳可能是行星加速度的物理原因。然而,牛顿在《原理》中指出,他从数学角度看待力,而不是从物理角度看,因此采取了一种工具主义的观点。[30] 此外,他没有给引力赋予一个具体的原因。[31]
牛顿定义作用在行星上的力为其质量与加速度的乘积(参见牛顿运动定律)。因此:
- 每颗行星都被太阳吸引。
- 作用在行星上的力与行星的质量成正比,与其距离太阳的平方成反比。
太阳在其中扮演着不对称的角色,这是没有依据的。因此,他在牛顿万有引力定律中假设:
- 太阳系中的所有天体互相吸引。
- 两天体之间的力与它们的质量乘积成正比,与它们之间的距离的平方成反比。
由于行星的质量相对于太阳较小,行星的轨道大致符合开普勒定律。牛顿的模型改进了开普勒的模型,并且更准确地符合实际观测结果。(参见二体问题)
以下是根据开普勒的第一定律和第二定律运动的行星加速度的详细计算。
加速度向量
从日心坐标系的角度考虑,指向行星的向量为 \(\mathbf{r} = r \hat{\mathbf{r}}\),其中 \(r\) 是到行星的距离,\(\hat{\mathbf{r}}\) 是指向行星的单位向量。 \[ \frac{d \hat{\mathbf{r}}}{dt} = \dot{\hat{\mathbf{r}}} = \dot{\theta} \hat{\boldsymbol{\theta}}, \quad \frac{d \hat{\boldsymbol{\theta}}}{dt} = \dot{\hat{\boldsymbol{\theta}}} = -\dot{\theta} \hat{\mathbf{r}}~ \] 其中,\(\hat{\boldsymbol{\theta}}\) 是与 \(\hat{\mathbf{r}}\) 的方向相反的单位向量,偏离 90 度,\(\theta\) 是极角,且变量上方的点表示对时间的微分。
对位置向量求两次导数,得到速度向量和加速度向量: \[ \dot{\mathbf{r}} = \dot{r} \hat{\mathbf{r}} + r \dot{\hat{\mathbf{r}}} = \dot{r} \hat{\mathbf{r}} + r \dot{\theta} \hat{\boldsymbol{\theta}},~ \] \[ \ddot{\mathbf{r}} = \left(\ddot{r} \hat{\mathbf{r}} + \dot{r} \dot{\hat{\mathbf{r}}}\right) + \left(\dot{r} \dot{\theta} \hat{\boldsymbol{\theta}} + r \ddot{\theta} \hat{\boldsymbol{\theta}} + r \dot{\theta} \dot{\hat{\boldsymbol{\theta}}}\right) = \left(\ddot{r} - r \dot{\theta}^2\right) \hat{\mathbf{r}} + \left(r \ddot{\theta} + 2 \dot{r} \dot{\theta}\right) \hat{\boldsymbol{\theta}}.~ \] 因此, \[ \ddot{\mathbf{r}} = a_r \hat{\boldsymbol{r}} + a_{\theta} \hat{\boldsymbol{\theta}},~ \] 其中,径向加速度为 \[ a_r = \ddot{r} - r \dot{\theta}^2,~ \] 而横向加速度为 \[ a_{\theta} = r \ddot{\theta} + 2 \dot{r} \dot{\theta}.~ \]
平方反比定律
开普勒的第二定律指出, \[ r^2 \dot{\theta} = nab~ \] 是恒定的。
横向加速度 \( a_{\theta} \) 为零: \[ \frac{d\left(r^2 \dot{\theta}\right)}{dt} = r \left( 2 \dot{r} \dot{\theta} + r \ddot{\theta} \right) = r a_{\theta} = 0.~ \] 因此,遵循开普勒第二定律的行星的加速度方向是指向太阳的。
径向加速度 \( a_r \) 为: \[ a_r = \ddot{r} - r \dot{\theta}^2 = \ddot{r} - r \left( \frac{nab}{r^2} \right)^2 = \ddot{r} - \frac{n^2 a^2 b^2}{r^3}.~ \] 开普勒的第一定律指出,轨道由以下方程描述: \[ \frac{p}{r} = 1 + \varepsilon \cos\left(\theta\right) .~ \] 对时间求导: \[ -\frac{p \dot{r}}{r^2} = -\varepsilon \sin\left(\theta\right) \dot{\theta},~ \] 或 \[ p \dot{r} = nab \varepsilon \sin\left(\theta\right) .~ \] 再对时间求导: \[ p \ddot{r} = nab \varepsilon \cos\left(\theta\right) \dot{\theta} = nab \varepsilon \cos\left(\theta\right) \frac{nab}{r^2} = \frac{n^2 a^2 b^2}{r^2} \varepsilon \cos\left(\theta\right) .~ \] 径向加速度 \( a_r \) 满足: \[ p a_r = \frac{n^2 a^2 b^2}{r^2} \varepsilon \cos\left(\theta\right) - p \frac{n^2 a^2 b^2}{r^3} = \frac{n^2 a^2 b^2}{r^2} \left( \varepsilon \cos\left(\theta\right) - \frac{p}{r} \right).~ \] 代入椭圆的方程得到: \[ p a_r = \frac{n^2 a^2 b^2}{r^2} \left( \frac{p}{r} - 1 - \frac{p}{r} \right) = - \frac{n^2 a^2}{r^2} b^2.~ \] 关系 \(b^2 = pa\) 给出简单的最终结果: \[ a_r = -\frac{n^2 a^3}{r^2}.~ \] 这意味着任何遵循开普勒第一定律和第二定律的行星的加速度向量 \[ \mathbf{\ddot{r}} = -\frac{\alpha}{r^2} \hat{\mathbf{r}}~ \] 满足平方反比定律,其中 \[ \alpha = n^2 a^3~ \] 是一个常数,\(\hat{\mathbf{r}}\) 是指向行星的单位向量,\(r\) 是行星与太阳之间的距离。
由于平均运动 \(n = \frac{2\pi}{T}\) 其中 \(T\) 是周期,根据开普勒的第三定律,\(\alpha\) 对所有行星都是相同的。因此,行星加速度的平方反比定律适用于整个太阳系。
平方反比定律是一个微分方程。这个微分方程的解包括开普勒的运动,如所示,但它也包括轨道是双曲线、抛物线或直线的运动。(参见开普勒轨道。)
牛顿的引力定律
根据牛顿的第二定律,作用于行星的引力为: \[ \mathbf{F} = m_{\text{planet}} \mathbf{\ddot{r}} = -m_{\text{planet}} \alpha r^{-2} \hat{\mathbf{r}},~ \] 其中 \( m_{\text{planet}} \) 是行星的质量,\(\alpha\) 对太阳系中所有行星具有相同的值。根据牛顿的第三定律,太阳也会受到与行星相等的引力。由于引力与行星的质量成正比,因此从对称的角度来看,它也应该与太阳的质量 \( m_{\text{Sun}} \) 成正比。因此: \[ \alpha = G m_{\text{Sun}},~ \] 其中 \( G \) 是引力常数。
根据牛顿定律,太阳系中第 \(i\) 个天体的加速度为: \[ \mathbf{\ddot{r}}_i = G \sum_{j \neq i} m_j r_{ij}^{-2} \hat{\mathbf{r}}_{ij},~ \] 其中 \( m_j \) 是天体 \( j \) 的质量,\( r_{ij} \) 是天体 \(i\) 和天体 \(j\) 之间的距离,\(\hat{\mathbf{r}}_{ij}\) 是从天体 \(i\) 指向天体 \(j\) 的单位向量,向量求和包括太阳系中除了 \(i\) 之外的所有天体。
在只有太阳和地球这两个天体的特例中,加速度为: \[ \mathbf{\ddot{r}}_{\text{Earth}} = G m_{\text{Sun}} r_{\text{Earth}, \text{Sun}}^{-2} \hat{\mathbf{r}}_{\text{Earth}, \text{Sun}},~ \] 这就是开普勒运动中的加速度。因此,地球按照开普勒定律围绕太阳运动。
如果太阳系中的两个天体是月球和地球,则月球的加速度为: \[ \mathbf{\ddot{r}}_{\text{Moon}} = G m_{\text{Earth}} r_{\text{Moon}, \text{Earth}}^{-2} \hat{\mathbf{r}}_{\text{Moon}, \text{Earth}}.~ \] 因此,在这个近似下,月球按照开普勒定律围绕地球运动。
在三体问题中,三体的加速度分别为: \[ \mathbf{\ddot{r}}_{\text{Sun}} = G m_{\text{Earth}} r_{\text{Sun}, \text{Earth}}^{-2} \hat{\mathbf{r}}_{\text{Sun}, \text{Earth}} + G m_{\text{Moon}} r_{\text{Sun}, \text{Moon}}^{-2} \hat{\mathbf{r}}_{\text{Sun}, \text{Moon}},~ \] \[ \mathbf{\ddot{r}}_{\text{Earth}} = G m_{\text{Sun}} r_{\text{Earth}, \text{Sun}}^{-2} \hat{\mathbf{r}}_{\text{Earth}, \text{Sun}} + G m_{\text{Moon}} r_{\text{Earth}, \text{Moon}}^{-2} \hat{\mathbf{r}}_{\text{Earth}, \text{Moon}},~ \] \[ \mathbf{\ddot{r}}_{\text{Moon}} = G m_{\text{Sun}} r_{\text{Moon}, \text{Sun}}^{-2} \hat{\mathbf{r}}_{\text{Moon}, \text{Sun}} + G m_{\text{Earth}} r_{\text{Moon}, \text{Earth}}^{-2} \hat{\mathbf{r}}_{\text{Moon}, \text{Earth}}.~ \] 这些加速度不是开普勒轨道的加速度,三体问题是复杂的。然而,开普勒近似是扰动计算的基础。(参见月球理论。)
6. 位置随时间变化的函数
开普勒利用他的前两条定律计算行星位置随时间的变化。这个方法涉及到解一个叫做 “开普勒方程” 的超越方程。
计算行星的日心极坐标(r,θ)作为自近日点以来时间 \(t\) 的函数的步骤如下:
- 计算平均运动 \(n = \frac{2\pi \ \text{rad}}{P}\),其中 \(P\) 是轨道周期。
- 计算平均近点角 \(M = nt\),其中 \(t\) 是自近日点以来的时间。
- 通过解开普勒方程计算偏近点角 \(E\): \[ M = E - \varepsilon \sin E,~ \] 其中 \(\varepsilon\) 是轨道的偏心率。
- 通过解以下方程计算真近点角 \(\theta\): \[ (1 - \varepsilon) \tan^2 \left( \frac{\theta}{2} \right) = (1 + \varepsilon) \tan^2 \left( \frac{E}{2} \right)~ \]
- 计算日心距离 \(r\): \[ r = a(1 - \varepsilon \cos E),~ \] 其中 \(a\) 是轨道的半长轴。
位置极坐标(r, θ)现在可以写成笛卡尔坐标系下的向量形式: \[ \mathbf{p} = r \left\langle \cos \theta, \sin \theta \right\rangle~ \] 然后,可以通过以下公式计算笛卡尔速度向量: \[ \mathbf{v} = \frac{\sqrt{\mu a}}{r} \left\langle -\sin E, \sqrt{1 - \varepsilon^2} \cos E \right\rangle~ \] 其中,\(\mu\) 是标准引力参数。
圆形轨道的特殊情况 (\(\varepsilon = 0\)) 给出了:\(\theta = E = M\) 因为匀速圆周运动被认为是正常的,因此从这种运动的偏差被视为异常。
这个过程的证明如下。
平均异常角,M
开普勒问题假设行星沿椭圆轨道运动,并考虑以下四个点:
- \(S\) 太阳(位于椭圆的一个焦点处);
- \(Z\) 近日点;
- \(C\) 椭圆的中心;
- \(P\) 行星。
定义如下:
- \( a = |CZ| \),椭圆中心到近日点的距离,半长轴;
- \( \varepsilon = \frac{|CS|}{a} \),偏心率;
- \( b = a \sqrt{1 - \varepsilon^2} \),半短轴;
- \( r = |SP| \),太阳与行星之间的距离;
- \( \theta = \angle ZSP \),从太阳看行星的方向,真实异常角。
问题的目标是根据从近日点起经过的时间 \( t \),计算行星的极坐标 \( (r, \theta) \)。
问题可以分步解决。开普勒考虑了以椭圆的长轴为直径的辅助圆,并定义如下:
- \(x\),行星在辅助圆上的投影;
- \(y\),辅助圆上使得扇形面积 \(|zcy|\) 和 \(|zsx|\) 相等的点;
- \( M = \angle zcy \),均 anomaly。
这些扇形面积的关系为: \[ |zsp| = \frac{b}{a} \cdot |zsx|~ \] 其中,圆形扇形的面积为: \[ |zcy| = \frac{a^2 M}{2}~ \] 自近日点以来扫过的面积为: \[ |zsp| = \frac{b}{a} \cdot |zsx| = \frac{b}{a} \cdot |zcy| = \frac{b}{a} \cdot \frac{a^2 M}{2} = \frac{abM}{2}~ \] 根据开普勒的第二定律,扇形面积与自近日点以来的时间成正比。因此,均 anomaly \( M \) 与自近日点以来的时间 \( t \) 成正比: \[ M = nt~ \] 其中,\( n \) 是均运动。
偏心异常,E
当计算均 anomaly \( M \) 后,目标是计算真实 anomaly \( \theta \)。然而,函数 \( \theta = f(M) \) 不是初等的。开普勒的解决方案是使用偏心异常 \( E \) 作为中间变量,其中 \( E = \angle zcx \),其中 \( x \) 是从椭圆中心看出去的点。开普勒的做法是首先通过求解下面的开普勒方程来计算 \( E \) 作为 \( M \) 的函数,然后从偏心异常 \( E \) 计算真实 anomaly \( \theta \)。以下是详细步骤。 扇形面积的关系为: \[ |zcy| = |zsx| = |zcx| - |scx|~ \] 其中, \[ |scx| = \frac{|cs| \cdot |dx|}{2}~ \] 开普勒的方程为: \[ \frac{a^2 M}{2} = \frac{a^2 E}{2} - \frac{a \varepsilon \cdot a \sin E}{2}~ \] 通过除以 \( \frac{a^2}{2} \),我们得到开普勒方程: \[ M = E - \varepsilon \sin E~ \] 此方程给出了 \( M \) 作为 \( E \) 的函数。对于给定的 \( M \),求解 \( E \) 是一个反问题,通常使用迭代数值算法来求解。
计算完偏心异常 \( E \) 后,下一步是计算真实 anomaly \( \theta \)。
但是需要注意的是,参考椭圆中心的笛卡尔坐标为:\((a \cos E, b \sin E)\)
相对于太阳(坐标为 \( (c, 0) = (ae, 0) \))的位置,\( r = (a \cos E - ae, b \sin E) \)。
真实 anomaly \( \theta \) 可以通过计算:\(\theta = \arctan \left( \frac{r_y}{r_x} \right)\) 而 \( r \) 的大小为:\(|r| = \sqrt{r_x^2 + r_y^2}\)
真实异常角,θ
从图中可以看出 \[ |cd| = |cs| + |sd|~ \] 因此 \[ a \cos E = a\varepsilon + r \cos \theta.~ \] 除以 \(a\) 并根据开普勒第一定律插入关系 \[ \frac{r}{a} = \frac{1 - \varepsilon^2}{1 + \varepsilon \cos \theta}~ \] 得到 \[ \cos E = \varepsilon + \frac{1 - \varepsilon^2}{1 + \varepsilon \cos \theta} \cos \theta = \frac{\varepsilon (1 + \varepsilon \cos \theta) + (1 - \varepsilon^2) \cos \theta}{1 + \varepsilon \cos \theta} = \frac{\varepsilon + \cos \theta}{1 + \varepsilon \cos \theta}.~ \] 结果是一个可用的关系式,连接偏心异常 \(E\) 和真实异常角 \(\theta\)。
通过代入三角恒等式,可以得到一个计算上更方便的形式: \[ \tan^2 \frac{x}{2} = \frac{1 - \cos x}{1 + \cos x}.~ \] 得到
距离 \(r\)
第四步是通过开普勒第一定律计算从真实异常角 \(\theta\) 得到的日心距离 \(r\): \[ r(1 + \varepsilon \cos \theta) = a(1 - \varepsilon^2).~ \] 利用上述 \(\theta\) 和 \(E\) 之间的关系,最终的距离方程为: \[ r = a(1 - \varepsilon \cos E).~ \]
7. 另见
- 圆周运动
- 自由下落时间
- 引力
- 开普勒轨道
- 开普勒问题
- 开普勒方程
- 拉普拉斯–朗格–伦茨矢量
- 特定相对角动量,基于角动量守恒的开普勒定律的相对容易推导
8. 解释说明
- 在 1621 年,约翰内斯·开普勒在他的《哥白尼天文学大成》([Epitome Astronomiae Copernicanae])中提到,木星的卫星(大约)遵循他的第三定律。该书出版于奥地利林茨(Lentiis ad Danubium)约翰·普兰克(Johann Planck)出版,1622 年,第四卷,第二部分,第 554–555 页。原文如下: "... 就像在太阳周围的六大行星中一样,... 马里乌斯在他自己的《木星世界》中提出了这一点,3.5.8.13(或 14.伽利略)... 而周期性时间则由同一马里乌斯给出... 它们大于简单的倍数,但小于双倍的倍数。” (……正如在太阳周围的六大行星之间明显为真一样,木星的四颗卫星也遵循类似规律,因为在木星的天体周围,任何能够远离木星的卫星,轨道运行速度都会减慢,而且其轨道周期与距离的比例并非完全相同,而是较大 [于距离],即每个距离的比例为 3/2(即 1.5),这正是六大行星所使用的比例。在他(马里乌斯)于 1614 年出版的《木星世界》一书中,他给出了木星四颗卫星的距离:3、5、8、13(或 14,伽利略所称)[注:木星卫星与木星的距离以木星直径的倍数表示]……马里乌斯给出的它们的周期时间为:1 天 18 小时 30 分钟,3 天 13 小时 30 分钟,7 天 2 小时,16 天 18 小时:对于所有这些数据,其比例大于简单的两倍,即大于 3、5、8、13 或 14 的比例,但小于距离平方数的比例,这些平方数分别是 9、25、64、169 或 196,正如 3/2 的比例大于 1 而小于 2 一样。)
- 戈德弗罗伊·温德林(Godefroy Wendelin)曾写信给乔瓦尼·巴蒂斯塔·里乔利(Giovanni Battista Riccioli),讨论木星卫星与木星之间的距离和它们的轨道周期之间的关系,证明这些周期和距离符合开普勒的第三定律。参见:乔瓦尼·巴蒂斯塔·里乔利,《新天文学大全》([Almagestum novum])(意大利博洛尼亚:维克托·贝纳蒂,1651 年),第 1 卷,第 492 页,Scholia III。相关段落旁边的边注写道:**Vendelini ingeniosa speculatio circa motus & intervalla satellitum Jovis**(温德林关于木星卫星运动和距离的巧妙推测)。来自第 492 页: "III. 温德林的推测不亚于开普勒的聪明才智... 他在 164/1000 年 7 月 7 日和 756/1000 年 16 日分别给出了内外卫星的周期比例。" (温德林,作为最聪明的天文学家之一,他对木星卫星的周期和距离比例的研究,与我在一封非常长且学术性的信件中详细交流过,他的研究成果也毫不逊色于开普勒的。正如大行星一样,行星与太阳的平均距离与周期的比例为 3/2;同样,木星的这几颗小卫星距离木星的距离(分别是 3、5、8 和 14)与它们的周期(分别为 1.769 天、3.554 天、7.164 天、16.756 天)也是按 3/2 的比例排列的。
9. 参考文献
- "Kepler's Laws". hyperphysics.phy-astr.gsu.edu. 取自 2022-12-13.
- "Orbits and Kepler's Laws". NASA Solar System Exploration. 取自 2022-12-13.
- "Planetary Motion: The History of an Idea That Launched the Scientific Revolution". earthobservatory.nasa.gov. 2009-07-07. 取自 2022-12-13.
- "Nicolaus Copernicus". history.com. 取自 2022-12-13.
- Gingerich, Owen (2011). "The great Martian catastrophe and how Kepler fixed it" (PDF). Physics Today. 64 (9): 50–54. Bibcode:2011PhT....64i..50G. doi:10.1063/PT.3.1259. 取自 2023 年 7 月 27 日.
-
- 伏尔泰,《牛顿哲学元素》[Elements of Newton's Philosophy](伦敦:1738 年)。例如,见: 第 162 页:“根据开普勒的伟大定律,每颗行星在相同的时间内扫过相等的面积;根据另一个同样可靠的定律,每颗行星围绕太阳的运动是这样的:如果它与太阳的平均距离为 10,则取该数的立方,即 1000,那么该行星围绕太阳的周期将与该数 1000 的平方根成正比。”
- 第 205 页:“因此,依据开普勒定律和牛顿定律,已证明每颗行星围绕太阳运动...”
- Wilson, Curtis (1994 年 5 月). "开普勒定律,所谓的" (PDF). HAD News (31): 1–2. 取自 2016 年 12 月 27 日.
- De la Lande, 《天文学》,第 1 卷(巴黎:Desaint & Saillant,1764 年)。例如,见:
- 第 390 页:“……但根据著名的开普勒定律,后面将在下册(第 892 条)中解释,该定律指出周期的比率总是大于距离的比率,譬如一颗距离太阳五倍远的行星,其公转周期大约是十二倍之多……”
- 第 429 页:“周期的平方与距离的立方成比例。892. 开普勒发现的最著名的行星运动定律是:行星轨道的大小与它们运行所需时间之间的关系;……”
- 第 430 页:“面积与时间成比例。895. 这一定律——行星运动中的一般定律——已成为天文学中如此重要的一部分,即面积与时间成比例,也是开普勒的发现之一;……”
- 第 435 页:“人们称这一定律为‘面积与时间成比例定律’(即开普勒定律),同样也称第 892 条中的定律,以纪念这位著名的发明家;……”
- Robert Small, 《开普勒天文发现记》(伦敦:J. Mawman,1804 年),第 298-299 页。
- Robert Small, 《开普勒天文发现记》(伦敦:J. Mawman,1804 年)。
- Bruce Stephenson (1994). 《开普勒的物理天文学》。普林斯顿大学出版社,第 170 页。ISBN 978-0-691-03652-6。
- 《新天文学》(Astronomia nova Aitiologitis),即《天体物理学传授:关于火星星体运动的评论,基于 G.V. Tycho 的观察》。布拉格,1609 年;英文版翻译:W.H. Donahue,剑桥,1992 年。
- 在《新天文学》中,开普勒仅提供了证明火星轨道是椭圆形的证据。关于其他已知行星轨道为椭圆形的证据,直到 1621 年才提出。 见:约翰内斯·开普勒,《新天文学》(1609 年),第 285 页。在排除圆形和椭圆形轨道后,开普勒得出结论,火星的轨道必须是椭圆形的。第 285 页顶部:“因此,椭圆是行星(即火星)轨道的路径;...” 同页后段:“... 如在下章中所揭示的:在此将同时证明,除了完美的椭圆形外,行星的轨道不可能是任何其他形状;...” 接着:“第 59 章。证明火星轨道... 是完美的椭圆:...” 火星轨道为椭圆的几何证明出现在第 289–290 页的《预定理 XI》中。 开普勒在《哥白尼天文学概要》中指出,每颗行星都在椭圆轨道上运行,太阳位于椭圆的一个焦点。见:约翰内斯·开普勒,《哥白尼天文学概要》(林茨(“Lentiis ad Danubium”),奥地利:约翰·普兰克,1622 年),第 5 卷,第 1 部分,III. 《轨道的形状》,第 658–665 页。 第 658 页:“行星的轨道是由椭圆构成的...” 第 659 页:“... 太阳(椭圆的另一个焦点)...”
- 霍尔顿,杰拉尔德·詹姆斯;布鲁什,斯蒂芬·G. (2001). 《物理学,人类的冒险:从哥白尼到爱因斯坦及其之后》(第三版平装本)。新泽西州皮斯卡塔维:罗格斯大学出版社,第 40-41 页。ISBN 978-0-8135-2908-0。取自 2009 年 12 月 27 日。
- 在《新天文学》(1609 年)中,开普勒并没有以现代形式呈现他的第二定律。他只有在 1621 年的《哥白尼天文学概要》中才提出了这一点。此外,在 1609 年,他以两种不同的形式提出了他的第二定律,学者们称之为 “距离定律” 和 “面积定律”。
- 他的 “距离定律” 出现在: “第 32 章,行星在圆形轨道上的运动所受的力,随着离源点的距离增大而减小。” 见:约翰内斯·开普勒,《新天文学》(1609 年),第 165-167 页。第 167 页中,开普勒写道:“...,由于αδ比αε长,行星在接近δ的离心轨道上停留的时间将比在接近ε的离心轨道上停留的时间要长。” 也就是说,行星离太阳越远(在点α处),它沿轨道的运动速度就越慢,因此,从太阳到行星的半径在相等的时间内扫过相等的面积。然而,正如开普勒所述,他的论证仅对圆形轨道适用,而不适用于椭圆形轨道。
- 他的 “面积定律” 出现在: “第 59 章,证明火星轨道... 是完美的椭圆:...”,《预定理 XIV 和 XV》,第 291-295 页。在第 294 页顶部写道:“椭圆的弧,时间由区域 AKN 测量,应该在 LK 处终止,以便它是 AM。” 换句话说,火星在其椭圆轨道上沿弧 AM 移动所需的时间是由椭圆段 AMN 的面积测量的(其中 N 是太阳的位置),而该面积又与围绕椭圆的圆的部分 AKN 成比例,并且该圆与椭圆相切。因此,太阳到火星的半径在火星沿椭圆轨道的弧段上扫过的面积与火星沿该弧段移动所需的时间成比例。也就是说,太阳到火星的半径在相等的时间内扫过相等的面积。
- 约翰内斯·开普勒,《宇宙和谐》(Linz,奥地利:约翰·普兰克,1619 年),第 5 卷,第 3 章,第 189 页。 第 189 页底部写道:“但是,绝对确定且精确的是,任意两个行星的周期时间之间的比例,恰好是它们平均距离的三比二比例(即 3:2 的比率)。” 开普勒的《宇宙和谐》英文版翻译为: 约翰内斯·开普勒,E. J. Aiton、A. M. Duncan 和 J. V. Field 译,《宇宙和谐》(美国宾夕法尼亚州:美国哲学学会,1997 年);特别见第 411 页。
- 国家地球科学教师协会(2008 年 10 月 9 日)。《行星和矮行星数据表》。世界之窗(Windows to the Universe)。2018 年 8 月 2 日检索。
- 尼古拉斯·梅尔卡托(1664 年)。《尼古拉斯·梅尔卡托的天文新假说及其与观测的符合》(拉丁文)。伦敦,英格兰:Leybourn。
- 梅尔卡托,尼古拉斯(1670 年 3 月 25 日)。“梅尔卡托先生关于卡西尼先生通过几何学和直接方法来求解行星的远日点、偏心率和偏差的一些思考;...”《伦敦皇家学会哲学学报》(拉丁文),第 5 卷,第 57 期,1168–1175 页。doi:10.1098/rstl.1670.0018。梅尔卡托批评了卡西尼通过三次观测来求解轨道近远点的方式。卡西尼错误地假设行星沿其椭圆轨道均匀运动。 第 1174 页:“但是,当他注意到这一假设与观测完全不符时,他改变了看法,并声明:一条表示行星真实运动的轨迹线,在相等时间内扫过椭圆的相等面积:...” (这是开普勒第二定律的 “面积” 形式)。
- Wilbur Applebaum(2000 年)《科学革命百科全书:从哥白尼到牛顿》。劳特利奇出版社,第 603 页。Bibcode:2000esrc.book.....A。ISBN 978-1-135-58255-5。
- Roy Porter(1992 年)《科学革命的国家背景》。剑桥大学出版社,第 102 页。ISBN 978-0-521-39699-8。
- Victor Guillemin; Shlomo Sternberg(2006 年)《开普勒主题的变奏》。美国数学学会,第 5 页。ISBN 978-0-8218-4184-6。
- Bryant, Jeff; Pavlyk, Oleksandr。“开普勒第二定律”,沃尔夫拉姆演示项目。检索于 2009 年 12 月 27 日。
- Holton, Gerald; Brush, Stephen(2001 年)《布鲁什与霍尔顿——物理学:人类的冒险》。普林斯顿大学出版社,第 42–43 页。ISBN 978-0813529080。
- Burtt, Edwin《现代物理科学的形而上学基础》,第 52 页。
- Gerald James Holton, Stephen G. Brush(2001 年)《物理学,人类的冒险》。罗格斯大学出版社,第 45 页。ISBN 978-0-8135-2908-0。
- Vijaya, G. K.(2019 年)《开普勒第三定律的原始形式及其在牛顿《原理》(第一卷)中的错误应用(命题 XXXII-XXXVII)》。*Heliyon*,5(2): e01274。Bibcode:2019Heliy...501274V。doi:10.1016/j.heliyon.2019.e01274。PMC 6395789。PMID 30886926。
- Caspar, Max(1993 年)《开普勒》。纽约:多佛出版公司,第 304 页。ISBN 9780486676050。
- Caspar, Max(1993 年)《开普勒》。纽约:多佛出版公司,第 286 页。ISBN 9780486676050。
- I. Newton,《原理》,I.B. Cohen 和 A. Whitman 翻译,第 408 页。
- I. Newton,《原理》,I.B. Cohen 和 A. Whitman 翻译,第 943 页。
- Schwarz, René。“备忘录 №1:开普勒轨道元素 → 笛卡尔状态向量”(PDF)。检索于 2018 年 5 月 4 日。
- Müller, M(1995 年)《时间方程——天文学中的问题》。*Acta Physica Polonica A*。检索于 2013 年 2 月 23 日。
10. 一般参考书目
- 开普勒的生平概述见第 523-627 页,他的伟大著作《世界和谐论》(Harmonices Mundi)的第五卷重新印刷在:Hawking, Stephen(编)(2002 年)《站在巨人肩膀上:物理学与天文学的伟大作品》。费城:Running Press,第 635-732 页。ISBN 978-0-7624-1348-5。
- 开普勒的行星运动第三定律的推导是工程力学课程中的标准话题。例如参见:Meriam, J. L.(1971 年)[1966 年],《动力学》(第 2 版)。纽约:Wiley,第 161-164 页。ISBN 978-0-471-59601-1。
- Murray, Carl D.; Dermott, S. F.(1999 年)《太阳系动力学》。剑桥;纽约:剑桥大学出版社。ISBN 978-0-521-57295-8。
- Arnolʹd, V. I.(1997 年)《第二章:运动方程的研究》。*经典力学的数学方法*(第二版)。数学研究生教材。纽约:Springer 出版公司。ISBN 978-0-387-96890-2。
11. 外部链接
- B. Surendranath Reddy; 开普勒定律的动画:小应用程序 [2013-10-06 已归档,来自 Wayback 机器]
- Crowell, Benjamin,《光与物质》,一本在线书籍,提供了不使用微积分的开普勒第一定律证明(见第 15.7 节)
- David McNamara 和 Gianfranco Vidali,《开普勒第二定律——Java 互动教程》,一个互动 Java 小程序,帮助理解开普勒的第二定律。
- Cain, Gay(2010 年 5 月 10 日),《天文学广播》,“第 189 集:约翰内斯·开普勒及其行星运动定律”
- 田纳西大学物理与天文学系:天文学 161,《约翰内斯·开普勒:行星运动定律》
- 太阳系模拟器(互动小程序)[2018 年 12 月 13 日已归档,来自 Wayback 机器]
- 《从星空观测者到星际飞船》中的 “开普勒及其定律” 由 David P. Stern(2016 年 10 月 10 日)
- 《开普勒的三大行星运动定律》在 YouTube 上由 Jens Puhle 发布(2023 年 12 月 27 日)——一段解释并可视化开普勒三大定律的视频。