库仑定律（综述）

                     

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章。

　　 库仑的反比平方定律，简称库仑定律，是一条物理学的实验定律[1]，用于计算静止的两个带电粒子之间的相互作用力。这种电力通常称为静电力或库仑力[2]。尽管这一定律早有认识，但它是在 1785 年由法国物理学家查尔-奥古斯丁·库仑首次公布的。库仑定律对于电磁学理论的发展至关重要，甚至可能是其起点[1]，因为它使得有意义的讨论粒子电荷量成为可能[3]。

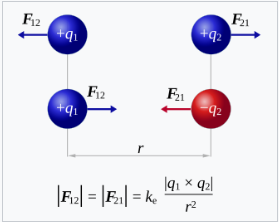
　　 该定律指出，两个点电荷之间的吸引或排斥静电力的大小（或绝对值）与它们电荷大小的乘积成正比，且与它们之间距离的平方成反比[4]。库仑发现，相同电荷的物体会相互排斥：

　　 因此，从这三个实验中可以得出结论：两个带有相同类型电荷的球体相互排斥的力，遵循与距离的平方成反比的规律[5]。

　　 库仑还表明，带相反电荷的物体会按照反比平方定律相互吸引： $$|F|=k_{\text{e}}\frac{|q_1||q_2|}{r^2}$$ 其中，$k_{\text{e}}$ 是常数，$q_1$ 和 $q_2$ 是两个电荷的电量，$r$ 是它们之间的距离。

　　 力的方向沿着连接两个电荷的直线。如果电荷具有相同的符号，静电力使它们相互排斥；如果电荷符号不同，静电力使它们相互吸引。

　　 作为一个反比平方定律，它类似于艾萨克·牛顿的万有引力反比平方定律，但引力总是使物体相互吸引，而静电力则使电荷相互吸引或排斥。此外，万有引力远弱于静电力[2]。库仑定律可以用来推导高斯定律，反之亦然。在静止的单个点电荷情况下，这两个定律是等效的，以不同的方式表达相同的物理规律[6]。这一定律已经被广泛验证，观测结果在从 ${10}^{-16}$ 米到 ${10}^8$ 米的尺度上都符合该定律[6]。

1. 历史

　　 地中海周围的古代文化知道某些物体，如琥珀棒，可以通过与猫毛摩擦来吸引轻物体，如羽毛和纸片。米利都的泰利斯大约在公元前 600 年首次记录了静电现象[7]，当时他注意到摩擦可以使一块琥珀吸引小物体[8][9]。

　　 1600 年，英国科学家威廉·吉尔伯特对电学和磁学进行了仔细研究，将磁铁效应与摩擦琥珀产生的静电区分开来[8]。他创造了新拉丁词 “electricus”（意为 “像琥珀一样” 或 “来自琥珀”，源自希腊语单词 ἤλεκτρον [elektron]，意为 “琥珀”），用来指代摩擦后能吸引小物体的性质[10]。这一联系促成了英语单词 “electric” 和 “electricity” 的诞生，它们首次出现在 1646 年托马斯·布朗的《伪常识》一书中[11]。

　　 18 世纪早期的研究者怀疑电力与重力一样会随距离衰减（即按距离的平方反比衰减），包括丹尼尔·伯努利[12]和亚历山德罗·伏打，他们都测量了电容器板之间的力，以及弗朗茨·艾皮努斯，他在 1758 年提出了反比平方定律[13]。

　　 基于电荷球体的实验，英国的约瑟夫·普里斯特利是最早提出电力遵循反比平方定律的科学家之一，类似于牛顿的万有引力定律。然而，他并未进一步推广或详细阐述这一点[14]。在 1767 年，他猜测电荷之间的力随距离的平方反比变化[15][16]。

　　 1769 年，苏格兰物理学家约翰·罗宾逊宣布，根据他的测量，两个带有相同电荷符号的球体之间的排斥力随距离变化为 $x^{-2.06}$[17]。

　　 在 1770 年代初期，英国的亨利·卡文迪许已经发现了带电物体之间的力与距离和电荷的关系，但并未发表[18]。在他的笔记中，卡文迪许写道：“因此我们可以得出结论，电吸引力和排斥力必定与距离的某种幂次成反比，其中 2 加 1/50 次方与 2 减 1/50 次方相差无几，而且没有理由认为它与反比平方的比例有所不同。”

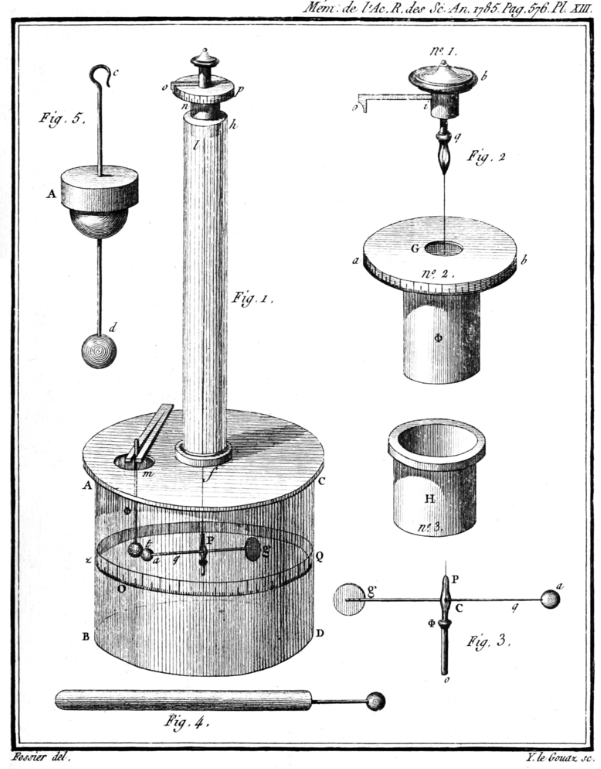
　　 最终，1785 年，法国物理学家查尔-奥古斯丁·库仑发表了他关于电学和磁学的三篇报告，首次提出了他的定律。这篇出版物对于电磁学理论的发展至关重要[4]。他使用了扭摆天平来研究带电粒子的排斥力和吸引力，并确定了两个点电荷之间的电力大小与电荷的乘积成正比，与它们之间距离的平方成反比。

2. 数学形式

　　 库仑定律表明，在真空中，某一电荷 $q_1$ 在位置 ${\mathbf{r}}_1$ 受到另一个电荷 $q_2$ 在位置 ${\mathbf{r}}_2$ 产生的静电力 ${\mathbf{F}}_1$ 为[19]： $${\mathbf{F}}_1=\frac{q_1{q}_2}{4\pi {\epsilon }_0}\frac{{\hat{\mathbf{r}}}_{12}}{|{\mathbf{r}}_{12}{|}^2}$$ 其中，${\mathbf{r}}_{12}={\mathbf{r}}_1-{\mathbf{r}}_2$ 是两个电荷之间的位移向量，${\hat{\mathbf{r}}}_{12}$ 是从 $q_2$ 指向 $q_1$ 的单位向量，${\epsilon }_0$ 是电常数。这里，${\hat{\mathbf{r}}}_{12}$ 用于表示向量的方向。根据牛顿第三定律，电荷 $q_2$ 受到的静电力 ${\mathbf{F}}_2$ 为： $${\mathbf{F}}_2=-{\mathbf{F}}_1$$ 如果两个电荷具有相同的符号（同种电荷），则乘积 $q_1{q}_2$ 为正，力的方向由 ${\hat{\mathbf{r}}}_{12}$ 给出；这时电荷互相排斥。如果电荷符号相反，则乘积 $q_1{q}_2$ 为负，力的方向为 $-{\hat{\mathbf{r}}}_{12}$；这时电荷互相吸引[20]。

离散电荷系统

　　 叠加原理使得库仑定律可以扩展到包括任意数量的点电荷。一个点电荷受到多个点电荷系统的作用力，可以通过将每个电荷单独作用于该点电荷的力向量相加得到。最终的力向量与该点的电场向量平行，而该点电荷已被移除。

　　 在真空中，位置为 $\mathbf{r}$ 的小电荷 $q$ 受到 $n$ 个离散电荷系统的作用力 $\mathbf{F}(\mathbf{r})$ 为[19]： $$\mathbf{F}(\mathbf{r})=\frac{q}{4\pi {\epsilon }_0}\sum _{i=1}^n{q}_i\frac{{\hat{\mathbf{r}}}_i}{|{\mathbf{r}}_i{|}^2}$$ 其中，$q_i$ 是第 $i$ 个电荷的电量，${\mathbf{r}}_i$ 是从第 $i$ 个电荷位置到 $\mathbf{r}$ 的向量，${\hat{\mathbf{r}}}_i$ 是指向 ${\mathbf{r}}_i$ 的单位向量。

连续电荷分布

　　 在这种情况下，线性叠加原理也适用。对于连续电荷分布，对包含电荷的区域进行积分等同于无限求和，将空间中的每个无穷小元看作一个点电荷 $dq$。电荷分布通常是线性的、表面分布的或体积分布的。

　　 对于线性电荷分布（如电线中的电荷），其中 $\lambda ({\mathbf{r}}^{\prime })$ 表示位置 ${\mathbf{r}}^{\prime }$ 处单位长度的电荷量，$d{\ell }^{\prime }$ 是一个无穷小的长度元[21]： $$d{q}^{\prime }=\lambda ({\mathbf{r}}^{\prime })d{\ell }^{\prime }.$$ 对于表面电荷分布（如平行板电容器板上的电荷），其中 $\sigma ({\mathbf{r}}^{\prime })$ 表示位置 ${\mathbf{r}}^{\prime }$ 处单位面积的电荷量，$d{A}^{\prime }$ 是一个无穷小的面积元： $$d{q}^{\prime }=\sigma ({\mathbf{r}}^{\prime })d{A}^{\prime }.$$ 对于体积电荷分布（如金属中的电荷），其中 $\rho ({\mathbf{r}}^{\prime })$ 表示位置 ${\mathbf{r}}^{\prime }$ 处单位体积的电荷量，$d{V}^{\prime }$ 是一个无穷小的体积元[20]： $$d{q}^{\prime }=\rho ({\mathbf{r}}^{\prime })d{V}^{\prime }.$$ 在真空中，位置为 $\mathbf{r}$ 的小测试电荷 $q$ 所受的力是通过对电荷分布进行积分得到的： $$\mathbf{F}(\mathbf{r})=\frac{q}{4\pi {\epsilon }_0}\int d{q}^{\prime }\frac{\mathbf{r}-{\mathbf{r}}^{\prime }}{|\mathbf{r}-{\mathbf{r}}^{\prime }{|}^3}.$$ 库仑定律的 “连续电荷” 版本不应应用于 $|\mathbf{r}-{\mathbf{r}}^{\prime }|=0$ 的位置，因为该位置会直接与带电粒子（如电子或质子）的位置重合，这不是经典电场或电势分析的有效位置。现实中电荷总是离散的，“连续电荷” 假设仅仅是一个近似，它不应该允许分析 $|\mathbf{r}-{\mathbf{r}}^{\prime }|=0$ 的情况。

3. 库仑常数

　　 库仑定律中的比例常数 $\frac{1}{4\pi {\epsilon }_0}$ 是单位选择的历史结果。[19]: 4–2

　　 常数 ${\epsilon }_0$ 是真空电介质常数。[22] 根据 CODATA 2022 推荐的 ${\epsilon }_0$ 值，[23] 库仑常数 [24] 为： $$k_{\text{e}}=\frac{1}{4\pi {\epsilon }_0}=8.9875517862(14)\times {10}^9\mathrm{N}\cdot {\mathrm{m}}^2\cdot {\mathrm{C}}^{-2}.$$

限制条件

　　 库仑的反平方定律有效性需要满足以下三个条件：[25]

1. 电荷必须具有球对称分布（例如，点电荷或带电金属球）。
2. 电荷不能重叠（例如，它们必须是不同的点电荷）。
3. 电荷必须相对于一个非加速的参考系静止。

　　 最后一个条件被称为静电近似。当电荷发生运动时，会引入一个额外的因素，这会改变两个物体之间的作用力。这一额外的力部分被称为磁力。在缓慢运动的情况下，磁力是最小的，库仑定律仍然可以近似地认为是正确的。然而，在这种情况下，一个更精确的近似是韦伯力。当电荷相对运动较快或发生加速时，必须考虑麦克斯韦方程和爱因斯坦的相对论理论。

电场

　　 电场是一个向量场，它将空间中的每个点与单位测试电荷所受的库仑力相关联。[19] 电荷 $q_t$ 所受的库仑力 $\mathbf{F}$ 的强度和方向取决于它所处位置的电场 $\mathbf{E}$，即：$\mathbf{F}=q_t\mathbf{E}$ 在最简单的情况下，电场被认为仅由一个源点电荷生成。更一般地，电场可以由一组电荷的分布产生，这些电荷通过叠加原理共同贡献。

　　 如果电场是由一个正点电荷 $q$ 产生的，则电场的方向沿着从源点辐射出去的径向线，即一个正点测试电荷 $q_t$ 如果被放置在电场中，它将沿着该方向运动。对于负点源电荷，电场方向则是径向指向源点。

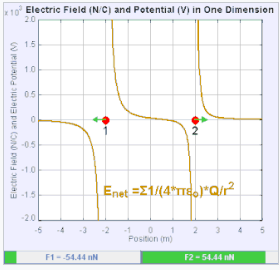
　　 电场强度 $E$ 的大小可以从库仑定律推导出来。通过选择一个点电荷作为源电荷，另一个作为测试电荷，根据库仑定律，单个源点电荷 $Q$ 在距离 $r$ 处产生的电场强度为： $$|\mathbf{E}|=k_{\text{e}}\frac{|q|}{r^2}$$ 一个由 $n$ 个离散电荷 $q_i$ 组成的系统，电荷位置为 ${\mathbf{r}}_i$，在位置 $\mathbf{r}$ 处产生的电场，其大小和方向由叠加原理给出： $$\mathbf{E}(\mathbf{r})=\frac{1}{4\pi {\epsilon }_0}\sum _{i=1}^n{q}_i\frac{{\hat{\mathbf{r}}}_i}{|{\mathbf{r}}_i{|}^2}$$

原子力

　　 库仑定律即使在原子内部也成立，能够正确描述带正电的原子核与每个带负电的电子之间的力。这一定律同样能正确解释将原子结合成分子、以及将原子和分子结合成固体和液体的力。一般来说，随着离子之间距离的增加，吸引力和结合能趋近于零，离子键合变得不那么有利。而当相反电荷的大小增加时，能量增加，离子键合变得更有利。

4. 与高斯定律的关系

从库仑定律推导高斯定律

　　 本节摘自《高斯定律 § 从库仑定律推导高斯定律》。 [需要引用] 严格来说，仅凭库仑定律无法推导出高斯定律，因为库仑定律仅给出单个静电点电荷所产生的电场。然而，如果再假设电场遵循叠加原理，那么可以从库仑定律推导出高斯定律。叠加原理指出，结果电场是由每个粒子产生的电场的向量和（或者，如果电荷在空间中平滑分布，则是积分）。
证明大纲
库仑定律指出，静止点电荷所产生的电场为： $$\mathbf{E}(\mathbf{r})=\frac{q}{4\pi {\epsilon }_0}\frac{{\mathbf{e}}_{\mathbf{r}}}{r^2}$$ 其中：

• ${\mathbf{e}}_{\mathbf{r}}$ 是径向单位向量，
• $r$ 是半径，$|r|$ 是距离，
• ${\epsilon }_0$ 是电常数，
• $q$ 是粒子的电荷量，假设粒子位于原点。

　　 使用库仑定律的表达式，我们通过积分将电场在 $r$ 处的总场计算出来，积分计算由空间中每个点 $s$ 处的微小电荷对 $r$ 处的电场贡献，得到： $$\mathbf{E}(\mathbf{r})=\frac{1}{4\pi {\epsilon }_0}\int \frac{\rho (\mathbf{s})(\mathbf{r}-\mathbf{s})}{|\mathbf{r}-\mathbf{s}{|}^3}{d}^3\mathbf{s}$$ 其中 $\rho$ 是电荷密度。如果我们对该方程两边分别对 $r$ 求散度，并使用已知定理： $$\mathrm{\nabla }\cdot \left(\frac{\mathbf{r}}{|\mathbf{r}{|}^3}\right)=4\pi \delta (\mathbf{r})$$ 其中 $\delta (\mathbf{r})$ 是狄拉克δ函数，结果为： $$\mathrm{\nabla }\cdot \mathbf{E}(\mathbf{r})=\frac{1}{{\epsilon }_0}\int \rho (\mathbf{s})\delta (\mathbf{r}-\mathbf{s})d^3\mathbf{s}$$ 使用狄拉克δ函数的 “筛选性质”，我们得到： $$\mathrm{\nabla }\cdot \mathbf{E}(\mathbf{r})=\frac{\rho (\mathbf{r})}{{\epsilon }_0}$$ 这就是高斯定律的微分形式，得证。

　　 由于库仑定律仅适用于静止电荷，因此仅基于这个推导没有理由期望高斯定律适用于运动电荷。实际上，高斯定律确实适用于运动电荷，在这一点上，高斯定律比库仑定律更为一般。
证明（不使用狄拉克δ函数）
令 $\mathrm{\Omega }\subseteq {\mathbb{R}}^3$ 为一个有界开集，并定义电场 ${\mathbf{E}}_0(\mathbf{r})$ 为 $${\mathbf{E}}_0(\mathbf{r})=\frac{1}{4\pi {\epsilon }_0}{\int }_{\mathrm{\Omega }}\frac{\rho ({\mathbf{r}}^{\prime })(\mathbf{r}-{\mathbf{r}}^{\prime })}{\Vert \mathbf{r}-{\mathbf{r}}^{\prime }{\Vert }^3}d{\mathbf{r}}^{\prime }\equiv \frac{1}{4\pi {\epsilon }_0}{\int }_{\mathrm{\Omega }}e(\mathbf{r},{\mathbf{r}}^{\prime })d{\mathbf{r}}^{\prime }$$ 其中 $\rho ({\mathbf{r}}^{\prime })$ 是连续函数（电荷密度）。

　　 对于所有 $\mathbf{r}\ne {\mathbf{r}}^{\prime }$，有 $${\mathrm{\nabla }}_{\mathbf{r}}\cdot \mathbf{e}(\mathbf{r},{\mathbf{r}}^{\prime })=0$$ 现在，考虑一个紧致集 $V\subseteq {\mathbb{R}}^3$，其边界 $\partial V$ 是分段光滑的，且满足 $\mathrm{\Omega }\cap V=\mathrm{\varnothing }$。由此可得，$\mathbf{e}(\mathbf{r},{\mathbf{r}}^{\prime })\in C^1(V\times \mathrm{\Omega })$，因此根据散度定理，有 $${\oint }_{\partial V}{\mathbf{E}}_0\cdot d\mathbf{S}={\int }_V\mathrm{\nabla }\cdot {\mathbf{E}}_{0}dV$$ 但是由于 $\mathbf{e}(\mathbf{r},{\mathbf{r}}^{\prime })\in C^1(V\times \mathrm{\Omega })$，我们有 $${\mathrm{\nabla }}_{\mathbf{r}}\cdot {\mathbf{E}}_0(\mathbf{r})=\frac{1}{4\pi {\epsilon }_0}{\int }_{\mathrm{\Omega }}{\mathrm{\nabla }}_{\mathbf{r}}\cdot \mathbf{e}(\mathbf{r},{\mathbf{r}}^{\prime })d{\mathbf{r}}^{\prime }=0$$ 根据以上推导（$\mathrm{\Omega }\cap V=\mathrm{\varnothing }⟹\mathrm{\forall }\mathbf{r}\in V,\mathrm{\forall }{\mathbf{r}}^{\prime }\in \mathrm{\Omega },\mathbf{r}\ne {\mathbf{r}}^{\prime }$），得到 ${\mathrm{\nabla }}_{\mathbf{r}}\cdot \mathbf{e}(\mathbf{r},{\mathbf{r}}^{\prime })=0$

　　 因此，通过闭合表面产生的电通量，由外部电荷密度（表面之外）生成的电通量为零。

　　 现在，考虑 ${\mathbf{r}}_0\in \mathrm{\Omega }$，并且 $B_R({\mathbf{r}}_0)\subseteq \mathrm{\Omega }$ 为以 ${\mathbf{r}}_0$ 为中心、半径为 $R$ 的球体（由于 $\mathrm{\Omega }$ 是开集，存在这样的球体）。

　　 令 ${\mathbf{E}}_{B_R}$ 和 ${\mathbf{E}}_C$ 分别为球体内部和外部生成的电场。则有： $${\mathbf{E}}_{B_R}=\frac{1}{4\pi {\epsilon }_0}{\int }_{B_R({\mathbf{r}}_0)}e(\mathbf{r},{\mathbf{r}}^{\prime })d{\mathbf{r}}^{\prime }$$ $${\mathbf{E}}_C=\frac{1}{4\pi {\epsilon }_0}{\int }_{\mathrm{\Omega }\setminus B_R({\mathbf{r}}_0)}e(\mathbf{r},{\mathbf{r}}^{\prime })d{\mathbf{r}}^{\prime }$$并且 ${\mathbf{E}}_{B_R}+{\mathbf{E}}_C={\mathbf{E}}_0$ $$\mathrm{\Phi }(R)={\oint }_{\partial B_R({\mathbf{r}}_0)}{\mathbf{E}}_0\cdot d\mathbf{S}={\oint }_{\partial B_R({\mathbf{r}}_0)}{\mathbf{E}}_{B_R}\cdot d\mathbf{S}+{\oint }_{\partial B_R({\mathbf{r}}_0)}{\mathbf{E}}_C\cdot d\mathbf{S}={\oint }_{\partial B_R({\mathbf{r}}_0)}{\mathbf{E}}_{B_R}\cdot d\mathbf{S}$$ 最后的等式是由于 $(\mathrm{\Omega }\setminus B_R({\mathbf{r}}_0))\cap B_R({\mathbf{r}}_0)=\mathrm{\varnothing }$，并且上述论证。

　　 右侧的电通量是由一个带电球体生成的电通量，因此有： $$\mathrm{\Phi }(R)=\frac{Q(R)}{{\epsilon }_0}=\frac{1}{{\epsilon }_0}{\int }_{B_R({\mathbf{r}}_0)}\rho ({\mathbf{r}}^{\prime })d{\mathbf{r}}^{\prime }=\frac{1}{{\epsilon }_0}\rho ({\mathbf{r}}_c^{\prime })|B_R({\mathbf{r}}_0)|$$ 其中 ${\mathbf{r}}_c^{\prime }\in B_R({\mathbf{r}}_0)$。

　　 最后的等式是通过积分的均值定理得到的。利用夹逼定理和电荷密度 $\rho$ 的连续性，可以得到： $$\mathrm{\nabla }\cdot {\mathbf{E}}_0({\mathbf{r}}_0)=\underset{R\to 0}{lim}\frac{1}{|B_R({\mathbf{r}}_0)|}\mathrm{\Phi }(R)=\frac{1}{{\epsilon }_0}\rho ({\mathbf{r}}_0)$$

从高斯定律推导库仑定律

　　 严格来说，库仑定律不能仅仅从高斯定律推导出来，因为高斯定律没有提供关于电场 $\mathbf{E}$ 的旋度的信息（参见赫尔姆霍兹分解和法拉第定律）。然而，如果再假设点电荷产生的电场是球对称的（这一假设对于静止电荷是完全正确的，对于运动电荷则近似成立），那么可以从高斯定律推导出库仑定律。
证明概要
将高斯定律的积分形式中的表面 $S$ 取为以点电荷 $Q$ 为中心、半径为 $r$ 的球面，我们得到 $${\oint }_S\mathbf{E}\cdot d\mathbf{A}=\frac{Q}{{\epsilon }_0}$$ 根据球对称性，积分中的被积函数是常数，可以将其提出积分之外。结果是 $$4\pi r^2\hat{\mathbf{r}}\cdot \mathbf{E}(\mathbf{r})=\frac{Q}{{\epsilon }_0}$$ 其中 $\hat{\mathbf{r}}$ 是指向电荷外部的单位向量。再次利用球对称性，电场 $\mathbf{E}$ 指向径向，因此我们得到 $$\mathbf{E}(\mathbf{r})=\frac{Q}{4\pi {\epsilon }_0}\frac{\hat{\mathbf{r}}}{r^2}$$ 这基本上等同于库仑定律。因此，库仑定律中电场的反比平方依赖性是由高斯定律推导得出的。

5. 在相对论中

　　 库仑定律可以用来深入理解运动电荷所产生的磁场，因为根据特殊相对论，在某些情况下，磁场可以被证明是由电场引起的力的变换。当粒子的历史中没有涉及加速度时，可以假设库仑定律适用于任何测试粒子在其惯性参考系中的情况，这一点通过对麦克斯韦方程求解时的对称性论证得到了支持。库仑定律可以扩展到运动测试粒子，保持相同的形式。这一假设得到了洛伦兹力定律的支持，洛伦兹力定律与库仑定律不同，并不限于静止的测试电荷。考虑到电荷对于观察者是恒定的，均匀运动的点电荷的电场和磁场可以通过洛伦兹变换从电荷参考系中给出的库仑定律中的四力推导出来，并通过洛伦兹力的形式来定义磁场和电场。 对于均匀运动的点电荷，得到的场为：[28] $$\mathbf{E}=\frac{q}{4\pi {ϵ}_0{r}^3}\frac{1-{\beta }^2}{(1-{\beta }^2{\sin }^2\theta {)}^{3/2}}\mathbf{r}$$ $$\mathbf{B}=\frac{q}{4\pi {ϵ}_0{r}^3}\frac{1-{\beta }^2}{(1-{\beta }^2{\sin }^2\theta {)}^{3/2}}\frac{\mathbf{v}\times \mathbf{r}}{c^2}=\frac{\mathbf{v}\times \mathbf{E}}{c^2}$$ 其中 $q$ 是点源的电荷， $\mathbf{r}$ 是从点源到空间中某点的位矢，$\mathbf{v}$ 是带电粒子的速度矢量， $\beta$ 是带电粒子速度与光速的比值，$\theta$ 是 $\mathbf{r}$ 与 $\mathbf{v}$ 之间的夹角。

　　 这种解的形式在特殊相对论框架下不必遵循牛顿第三定律（但不违反相对论能量-动量守恒）。[29]注意，电场的表达式在非相对论性速度下会简化为库仑定律，且在非相对论极限下（近似 $\beta \ll 1$）磁场可以应用于电流，得到比奥–萨伐尔定律。这些解在用迟延时间表示时，也对应于麦克斯韦方程的一般解，这些解通过 Liénard–Wiechert 位势给出，因库仑定律在其特定应用范围内的有效性。同样需要注意，静止电荷下高斯定律的球对称性不适用于运动电荷，因为在问题中存在速度方向的指定，破坏了对称性。上述两个方程也可以手动验证与麦克斯韦方程的一致性。[30]

6. 库仑势能

量子场论

　　 库仑势能允许连续态（当 $E>0$ 时），描述电子-质子散射，同时也允许离散束缚态，表示氢原子[31]。它还可以在非相对论极限下推导出，描述两颗带电粒子之间的相互作用，具体如下：

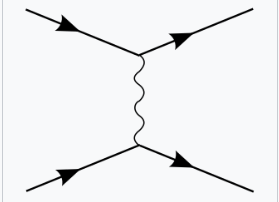
　　 在玻恩近似下，在非相对论量子力学中，散射振幅 $\mathcal{A}(|\mathbf{p}⟩\to |{\mathbf{p}}^{\prime }⟩)$ 为： $$\mathcal{A}(|\mathbf{p}⟩\to |{\mathbf{p}}^{\prime }⟩)-1=2\pi \delta (E_p-E_{p^{\prime }})(-i)\int d^3\mathbf{r}V(\mathbf{r})e^{-i(\mathbf{p}-{\mathbf{p}}^{\prime })\mathbf{r}}$$ 这与以下表达式进行比较： $$\int \frac{d^{3}k}{(2\pi {)}^3}{e}^{ik{r}_0}⟨p^{\prime },k|S|p,k⟩$$ 在这里，我们查看两个电子相互散射的（连接的）S 矩阵项，将一个电子的 “固定” 动量视为势的源，另一个电子则散射在这个势上。

　　 使用费曼规则计算 S 矩阵元素，在非相对论极限下 ($m_0\gg |\mathbf{p}|$) 得到： $$⟨p^{\prime },k|S|p,k⟩{|}_{conn}=-i\frac{e^2}{|\mathbf{p}-{\mathbf{p}}^{\prime }{|}^2-i\epsilon }(2m{)}^2\delta (E_{p,k}-E_{p^{\prime },k})(2\pi {)}^4\delta (\mathbf{p}-{\mathbf{p}}^{\prime })$$ 与量子力学散射相比，我们必须去掉 $(2m{)}^2$，因为在量子场论（QFT）中，动量本征态的归一化与量子力学（QM）不同，因此得到： $$\int V(\mathbf{r})e^{-i(\mathbf{p}-{\mathbf{p}}^{\prime })\mathbf{r}}{d}^3\mathbf{r}=\frac{e^2}{|\mathbf{p}-{\mathbf{p}}^{\prime }{|}^2-i\epsilon }$$ 通过对两边进行傅里叶变换，解出积分并最终取 $\epsilon \to 0$，会得到： $$V(r)=\frac{e^2}{4\pi r}$$ 这是库仑势能[32]。

　　 然而，经典 Born 推导中库仑问题的等效结果被认为是完全偶然的[33][34]。

　　 库仑势能及其推导可以看作是尤卡瓦势能的特例，其中交换的玻色子——光子——没有静质量[31]。

7. 验证

　　 “验证

　　 可以通过一个简单的实验来验证库仑定律。考虑两个质量为 $m$ 且带有相同电荷 $q$ 的小球，悬挂在两根质量可以忽略的长度为 $l$ 的绳子上。作用在每个小球上的力有三种：重力 $mg$、绳子的张力 $\mathbf{T}$ 和电力 $\mathbf{F}$。在平衡状态下：

　　 $$\begin{array}{}\text{(1)}& \mathbf{T}\sin {\theta }_1={\mathbf{F}}_1\end{array}$$ 和 $$\begin{array}{}\text{(2)}& \mathbf{T}\cos {\theta }_1=mg\end{array}$$

　　 将式（1）除以式（2）得到： $$\begin{array}{}\text{(3)}& \frac{\sin {\theta }_1}{\cos {\theta }_1}=\frac{F_1}{mg}\Rightarrow F_1=mg\tan {\theta }_1\end{array}$$

　　 设 ${\mathbf{L}}_1$ 为带电小球之间的距离，假设库仑定律正确，则它们之间的斥力 $F_1$ 为： $$F_1=\frac{q^2}{4\pi {\epsilon }_0{L}_1^2}\text{(库仑定律)}$$ 所以： $$\begin{array}{}\text{(4)}& \frac{q^2}{4\pi {\epsilon }_0{L}_1^2}=mg\tan {\theta }_1\end{array}$$ 现在，如果我们放电一个小球，并将其与带电小球接触，那么它们每个将获得 $\frac{q}{2}$ 的电荷。在平衡状态下，带电小球之间的距离将变为 $L_2<L_1$，它们之间的斥力为： $$\begin{array}{}\text{(5)}& F_2=\frac{{\left(\frac{q}{2}\right)}^2}{4\pi {\epsilon }_0{L}_2^2}=\frac{\frac{q^2}{4}}{4\pi {\epsilon }_0{L}_2^2}\end{array}$$ 我们知道：$F_2=mg\tan {\theta }_2$ 因此： $$\frac{\frac{q^2}{4}}{4\pi {\epsilon }_0{L}_2^2}=mg\tan {\theta }_2$$ 将式（4）除以式（5），我们得到： $$\begin{array}{}\text{(6)}& \frac{\left(\frac{q^2}{4\pi {\epsilon }_0{L}_1^2}\right)}{\left(\frac{\frac{q^2}{4}}{4\pi {\epsilon }_0{L}_2^2}\right)}=\frac{mg\tan {\theta }_1}{mg\tan {\theta }_2}\Rightarrow 4{\left(\frac{L_2}{L_1}\right)}^2=\frac{\tan {\theta }_1}{\tan {\theta }_2}\end{array}$$ 测量角度 ${\theta }_1$ 和 ${\theta }_2$ 以及带电小球之间的距离 $L_1$ 和 $L_2$ 足以验证等式的正确性，同时考虑到实验误差。实际上，测量角度可能会很困难，因此，如果绳子的长度足够大，角度会足够小，可以做以下近似： $$\begin{array}{}\text{(7)}& \tan \theta \approx \sin \theta =\frac{L}{2\ell }\Rightarrow \frac{\tan {\theta }_1}{\tan {\theta }_2}\approx \frac{\frac{L_1}{2\ell }}{\frac{L_2}{2\ell }}\end{array}$$ 使用这个近似，关系式（6）变为更简单的表达式： $$\begin{array}{}\text{(8)}& \frac{\frac{L_1}{2\ell }}{\frac{L_2}{2\ell }}\approx 4{\left(\frac{L_2}{L_1}\right)}^2\Rightarrow \frac{L_1}{L_2}\approx 4{\left(\frac{L_2}{L_1}\right)}^2\Rightarrow \frac{L_1}{L_2}\approx \sqrt[3]{4}\end{array}$$ 通过这种方式，验证的过程仅限于测量带电小球之间的距离，并检查分值是否接近理论值。

8. 另见

• 比奥-萨伐尔定律
• 达尔文拉格朗日量
• 电磁力
• 高斯定律
• 镜像电荷法
• 分子建模
• 牛顿万有引力定律（结构相似，但用于质量而非电荷）
• 静力和虚粒子交换
• 卡西米尔效应

9. 参考文献

1. Huray, Paul G. (2010). 《麦克斯韦方程》. 新泽西州霍博肯: Wiley. 第 8, 57 页. ISBN 978-0-470-54991-9. OCLC 739118459.
2. Halliday, David; Resnick, Robert; Walker, Jearl (2013). 《物理学基础》. John Wiley & Sons. 第 609, 611 页. ISBN 9781118230718.
3. Roller, Duane; Roller, D. H. D. (1954). 《电荷概念的发展：从希腊到库仑的电学》.马萨诸塞州剑桥: 哈佛大学出版社. 第 79 页.
4. Coulomb (1785). “关于电和磁的首篇论文”. 《皇家科学院史》 (法语). 第 569–577 页.
5. Coulomb (1785). “关于电和磁的第二篇论文”. 《皇家科学院史》 (法语). 第 578–611 页. “因此，从这三次实验中可以得出，两个带有同种电的球之间的排斥力遵循距离平方的反比规律。”
6. Purcell, Edward M. (2013 年 1 月 21 日). 《电与磁》(第 3 版). 剑桥大学出版社. ISBN 9781107014022.
7. Cork, C.R. (2015). “电子纺织品用导电纤维”. 《电子纺织品》: 3–20. doi:10.1016/B978-0-08-100201-8.00002-3. ISBN 9780081002018.
8. Stewart, Joseph (2001). 《中级电磁理论》. World Scientific. 第 50 页. ISBN 978-981-02-4471-2.
9. Simpson, Brian (2003). 《电刺激与疼痛缓解》. Elsevier Health Sciences. 第 6–7 页. ISBN 978-0-444-51258-1.
10. Baigrie, Brian (2007). 《电与磁：历史视角》. Greenwood Press. 第 7–8 页. ISBN 978-0-313-33358-3.
11. Chalmers, Gordon (1937). “磁石与 17 世纪英国对物质的理解”. 《科学哲学》. 4 (1): 75–95. doi:10.1086/286445. S2CID 121067746.
12. Socin, Abel (1760). 《瑞士物理-数学-解剖-植物-医学报》 (拉丁语). 第 4 卷. 巴塞尔. 第 224–225 页.
13. Heilbron, J.L. (1979). 《17 和 18 世纪的电学：早期现代物理学研究》. 加利福尼亚州洛杉矶: 加州大学出版社. 第 460–462 页和 464 页（包含注释 44）. ISBN 978-0486406886.
14. Schofield, Robert E. (1997). 《约瑟夫·普里斯特里的启蒙：1733 至 1773 年其生活与工作的研究》. 宾夕法尼亚州立大学出版社. 第 144–156 页. ISBN 978-0-271-01662-7.
15. Priestley, Joseph (1767). 《电学的历史与现状，附原始实验》. 英国伦敦. 第 732 页.
16. Elliott, Robert S. (1999). 《电磁学：历史、理论与应用》. Wiley 出版社. ISBN 978-0-7803-5384-8. 原始版本存档于 2014 年 3 月 10 日，检索于 2009 年 10 月 17 日.
17. Robison, John (1822). 由 Murray, John (编辑). 《机械哲学系统》. 第 4 卷. 英国伦敦: J. Murray 印刷.
18. Maxwell, James Clerk, ed. (1967) [1879]. “电力实验：电力定律的实验确定”. 《尊敬的亨利·卡文迪许的电学研究…》 (第一版). 英国剑桥: 剑桥大学出版社. 第 104–113 页.
19. Feynman, Richard P. (1970). 《费曼物理学讲义 第二卷》. Addison-Wesley 出版社. ISBN 9780201021158.
20. Fitzpatrick, Richard (2006-02-02). “库仑定律”. 得克萨斯大学. 原始内容存档于 2015-07-09，检索于 2007-11-30.
21. “带电棒”. PhysicsLab.org. 原始内容存档于 2014-10-10，检索于 2007-11-06.
22. 《国际单位制》(PDF) (第 9 版), 国际度量衡局, 2022 年 12 月, 第 15 页, ISBN 978-92-822-2272-0.
23. “2022 CODATA 值：真空电容率”. NIST 常数、单位和不确定性参考. 美国国家标准与技术研究院 (NIST). 原始内容存档于 2024-06-24，检索于 2024-10-27.
24. Serway, Raymond A.; Jewett, John W., Jr. (2014). “一些物理常数”. 《科学家和工程师的物理学》(第九版). Cengage Learning 出版社. 封底. ISBN 978-1-133-95405-7.
25. W. Shao; B. Jiang; J.K. Lv (2015). “物理教学创新讨论：以库仑定律为例”. 见 Dawei Zheng (ed.). 《教育管理与管理科学》. CRC 出版社. 第 465–468 页. doi:10.1201/b18636-105. ISBN 978-0-429-22704-2.
26. 例如，Griffiths, David J. (2013). 《电动力学导论》(第 4 版). Prentice Hall 出版社. 第 50 页；或 Jackson, John David (1999). 《经典电动力学》(第 3 版). John Wiley & Sons 出版社. 第 35 页.
27. Rosser, W. G. V. (1968). 《通过相对论的经典电磁学》. 第 29–42 页. doi:10.1007/978-1-4899-6559-2. ISBN 978-1-4899-6258-4. 原始内容存档于 2022-10-09，检索于 2022-10-09.
28. Heaviside, Oliver (1894). 《电磁波、势的传播以及运动电荷的电磁效应》. 原始内容存档于 2022-10-09，检索于 2022-10-09.
29. Griffiths, David J. (1999). 《电动力学导论》(第 3 版). 新泽西州 Upper Saddle River: Prentice Hall 出版社. 第 517 页. ISBN 0-13-805326-X. OCLC 40251748.
30. Purcell, Edward (2011-09-22). 《电与磁》. 剑桥大学出版社. doi:10.1017/cbo9781139005043. ISBN 978-1-107-01360-5. 原始内容存档于 2023-12-30，检索于 2022-10-09.
31. Griffiths, David J. (2018 年 8 月 16 日). 《量子力学导论》(第三版). 英国剑桥. ISBN 978-1-107-18963-8.
32. “量子场论 I + II” (PDF). 海德堡大学理论物理研究所. 原始内容(PDF)存档于 2021-05-04，检索于 2020-09-24.
33. Baym, Gordon (2018). 《量子力学讲义》. 博卡拉顿. ISBN 978-0-429-49926-5. OCLC 1028553174.
34. Gould, Robert J. (2020 年 7 月 21 日). 《电磁过程》. 普林斯顿，新泽西. ISBN 978-0-691-21584-6. OCLC 1176566442.

　　 Spavieri, G., Gillies, G. T., & Rodriguez, M. (2004). 库仑定律的物理意义. 《计量学》, 41(5), S159–S170. doi:10.1088/0026-1394/41/5/s06

10. 相关阅读

• Coulomb, Charles Augustin (1788) [1785]. “关于电和磁的首篇论文”. 《皇家科学院史》. 皇家印刷局. 第 569–577 页.
• Coulomb, Charles Augustin (1788) [1785]. “关于电和磁的第二篇论文”. 《皇家科学院史》. 皇家印刷局. 第 578–611 页.
• Coulomb, Charles Augustin (1788) [1785]. “关于电和磁的第三篇论文”. 《皇家科学院史》. 皇家印刷局. 第 612–638 页.
• Griffiths, David J. (1999). 《电动力学导论》(第 3 版). Prentice Hall 出版社. ISBN 978-0-13-805326-0.
• Tamm, Igor E. (1979) [1976]. 《电学理论基础》(第 9 版). 莫斯科: Мир出版社. 第 23–27 页.
• Tipler, Paul A.; Mosca, Gene (2008). 《科学家和工程师的物理学》(第 6 版). 纽约: W. H. Freeman and Company. ISBN 978-0-7167-8964-2. LCCN 2007010418.
• Young, Hugh D.; Freedman, Roger A. (2010). 《西尔斯与泽曼斯基大学物理学：现代物理学》(第 13 版). Addison-Wesley (Pearson 出版社). ISBN 978-0-321-69686-1.