无限深势阱中的高斯波包数值计算(Matlab)
贡献者: 待更新
- 本文处于草稿阶段。
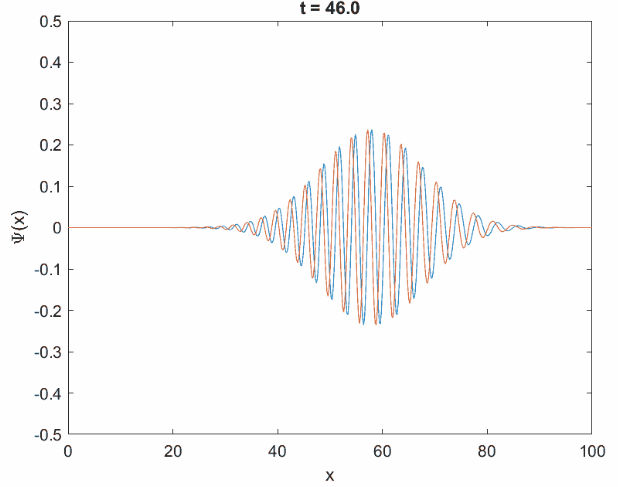
图 1:运行结果,动画见这里。
代码 1:WpkISW.m
% 无限深势阱中的波包
close all; clear; % 关闭所有画图, 清空所有变量
% === 参数 ===
L = 100; % 势阱区间 [0, L]
sig_x = 4; % 波包宽度
x0 = 50; % 波包初始位置
k0 = 2; % 波包初始动量
Nbasis = 100; % 基底数量
Nx = 501; % 画图格点数
tmax = 100; % 演化时间 [0, tmax]
Nt = 201; % 演化步数
% ============
sig_k = 1/(2*sig_x); % 动量谱宽度
Ax = 1/(2*pi*sig_x^2)^0.25; % x 归一化系数
Ak = 1/(2*pi*sig_k^2)^0.25; % k 归一化系数
% x 和 k 的波函数
f = @(x) Ax * exp(-((x - x0)/(2*sig_x)).^2) .* exp(1i*k0*x);
g = @(k) Ak * exp(-((k - k0)/(2*sig_k)).^2) .* exp(-1i*x0*(k-k0));
% 位置,时间动量格点
x = linspace(0, L, Nx);
t = linspace(0, tmax, Nt);
% 初始波包投影系数
k = (1:Nbasis) * pi / L;
coeff = 1i*sqrt(pi/L)*(g(k) - g(-k));
% 画图判断系数是否收敛
coeff2 = abs(coeff).^2;
figure; plot(coeff2);
title(['sum(|coeff|^2) = ' num2str(sum(coeff2))]);
figure;
for it = 1:Nt
% 计算 t(it) 时刻的波函数
psi = zeros(1, Nx);
for i = 1:Nbasis
Eng = 0.5*k(i)^2;
psi = psi + coeff(i) * exp(-1i*Eng*t(it)) * sqrt(2/L) * sin(i*pi*x/L);
end
% 画出波函数实部和虚部
clf; plot(x, real(psi));
hold on; plot(x, imag(psi));
xlabel x; ylabel \Psi(x);
title(['t = ' num2str(t(it), '%.1f')]);
axis([0, L, -0.5, 0.5]);
drawnow;
% 取消注释可将每一帧保存为 png 图片(当前目录下)
saveas(gcf, [num2str(it) '.png']);
end