IDA-star 算法

贡献者：有机物

预备知识　迭代加深，A-star 算法

　　 IDA* 算法是加了估价函数的迭代加深。

　　 A* 算法是在优先队列 BFS 上加了估价函数，估价函数也当然可以和 DFS 结合，但如果只是和最普通的 DFS 结合在一起很容易出现搜索深度很深，但答案深度很浅的情况，所以可以将迭代加深 DFS 和估价函数结合在一起，就形成了 IDA-star 算法。IDA* 算法的估价函数和 A* 非常类似，都是表示当前状态到目标状态的估计距离，IDA* 当然也要满足估计距离不大于真实距离这个前提。IDA* 使用迭代的框架，如果当前深度加估计距离大于深度限制，则直接回溯。

　　 IDA* 的框架：

int f();   // 估价函数

// depth 当前搜索层数，max_depth 为迭代加深的搜索深度限制
bool dfs(int depth, int max_depth)  
{
    // 如果当前层数 + 估价函数 > 深度限制，则直接回溯
    if (depth + f() > max_depth) return false; 
    if (!f()) return true;  // 一般估价函数为 0 说明找到了答案
    
    /*
    以下为 dfs 内容
    */
    
    return false;   // 找不到答案就回溯
}

int main()
{
    int depth = 0;
    while (!dfs(0, depth)) depth ++ ;   // 迭代加深
    
    return 0;
}

　　 例题 $1$：排书

　　题目大意：每次可以将打乱的图书的一段取出放到其他位置的后面，问最少需要多少次可以将打乱的图书按照递增的顺序排列。

　　首先确定搜索顺序：枚举序列中每一段的图书摆到哪些位置，对于一段图书摆到一个位置的前面或者一个位置的后面是等价的，所以只需枚举摆到后面，摆的位置从选的那一段图书的右端点的位置加一开始枚举。这样就可以不遗漏的枚举出每种状态。

　　设计估价函数：设定一个正确/错误后继的概念，若一个图书 $i$，如果按照递增的顺序排列，它的下一个位置应该是 $i + 1$，我们称 $i + 1$ 是 $i$ 的正确后继，错误后继显然就是图书 $i$ 后面不是 $i + 1$ 的情况。

　　想要将一个打乱的图书变为递增的序列，显然序列中错误的后继数为 $0$，所以我们统计一个图书序列中错误的后继数，记为 $\tt cnt$，可以发现每次操作最多更改三本书的后继，若每次操作是最理想的，将一个乱序变为递增的序列最少也需要 $\left\lceil\dfrac{\tt cnt}{3}\right\rceil$ 次操作，满足估价函数的前提。故可将估价函数设计为 $f(\tt state) = \left\lceil\dfrac{\tt cnt}{3}\right\rceil$。

　　所以深度从 $1 \sim 4$ 增加，每次枚举序列中的每一段数放在哪些位置的后面，若当前深度加估价函数大于深度限制，则直接回溯，回溯时记得要恢复现场。

　　 时间复杂度： $\mathcal{O}(\dfrac{(n - 1) \times n \times (n + 1)}{6}) = 560^4$。

　　对于整个图书中每次选择的一段图书，假设要选择的图书长度为 $i$，则一共有 $n - i + 1$ 种选法，这样还剩 $n - i$ 本书，还有 $n - i + 1$ 个位置可以放，所以一共有 $(n - i + 1) \times (n - i)$ 种选择，前面提到了，将一段书放在一个的位置的前面或后面没有区别，所以需要除二。

　　 $i$ 从 $1 \sim 15$ 开始枚举，因此总共的选法有：

　　 $\dfrac{15 \times 14 + 14 \times 13 + \cdots + 2 \times 1}{2}$ 种。

　　因为 $n \times (n - 1) + (n - 1) \times (n - 2) + \cdots + 2 \times 1 = \dfrac{(n - 1) \times n \times (n + 1)}{3}$。

　　所以对于一个长度为 $n$ 的序列，总的选法为 $\dfrac{(n - 1) \times n \times (n + 1)}{6}$。

　　虽然理论的时间复杂度为 $\mathcal{O}(560^4)$，但 IDA* 的实际效率很高。

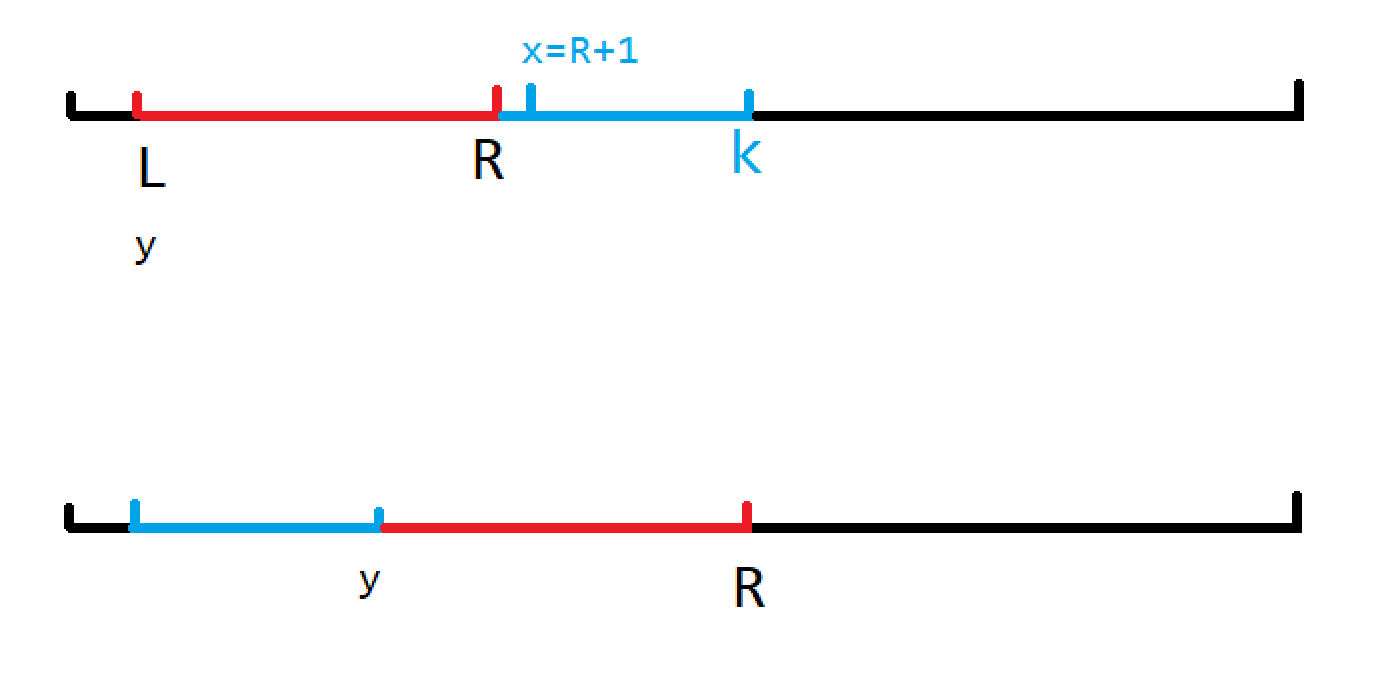
　　还有一个细节就是如何将一段书放到一个位置的后面呢？可以使用一个数组 $W$，详细的可以看下图和代码。

图 1：示意图

　　 C++ 代码：

const int N = 20;
int n, q[N], w[5][N];

// 估价函数，为当前序列中错误的后继的个数
int f()
{
    int cnt = 0;
    for (int i = 0; i + 1 < n; i ++ )
        if (q[i + 1] != q[i] + 1)
            cnt ++ ;
    return (cnt + 2) / 3;
}

bool dfs(int u, int depth)
{
    // 迭代加深
    if (u + f() > depth) return false;
    if (!f()) return true;  // 错误的后继为 0，说明序列单调递增

    for (int len = 1; len <= n; len ++ )  // 枚举序列长度
        for (int l = 0; l + len - 1 < n; l ++ ) // 枚举左端点
        {
            int r = l + len - 1;    // 右端点
            for (int k = r + 1; k < n; k ++ )   // 枚举能插入的位置
            {
                memcpy(w[u], q, sizeof q);  // 备份一下，为后面的回溯做准备

                // 将一段数 [l, r] 插到从 k 的后面
                int y = l;  
                for (int x = r + 1; x <= k; x ++ , y ++ ) q[y] = w[u][x];
                for (int x = l; x <= r; x ++ , y ++ ) q[y] = w[u][x];

                if (dfs(u + 1, depth)) return true;
                memcpy(q, w[u], sizeof q);  // 回溯时要恢复现场
            }
        }

    return false;
}

　　 例题 $2$：回转游戏

　　首先确定一下搜索顺序，对于每个状态，每次枚举当下的八种操作，可以发现一个剪枝优化，每个操作对应着有个逆操作，例如先操作了 $A$ 操作，下次就不要再操作 $F$ 了，所以每次操作前可以判断一下当前操作是不是上一个操作的逆操作。

　　搜索树的深度很深，但答案应该不会太深，所以可以使用迭代加深，加一个估价函数，就变成了 IDA*。为了要使井形棋盘最中间的 $8$ 个格子里的数字相同，如果中间 $8$ 个格子里的数字出现次数最多为 $k$，还有其他的 $8 - k$ 个数字，则最少还需 $8 - k$ 次操作，所以可以设计估价函数为 $f(\texttt{state}) = 8 - k$。

　　棋盘中的操作比较复杂，所以可以将棋盘中每个数字给予一个编号，首先打表出 $8$ 个操作对应的数字的编号。再打表出每个操作对应的逆操作，比如 $A$ 对应着 $F$，$8$ 种操作为 $A \sim H$，对应着 $0 \sim 7$。又因为估价函数需要中间的 $8$ 个数字，所以还需打表出中间的 $8$ 个数字的编号。善用打表可以使代码变得简洁。

　　 时间复杂度： $\mathcal{O}(7^k)$。

　　如果最少的操作步数为 $k$ 步，那么需要枚举 $7$ 种操作（去除了对应的逆操作），所以最坏情况下需要枚举 $7^k$ 种情况，但实际效率远小于理论时间复杂度。

　　 C++ 代码：

/*
棋盘的编号：
      0     1
      2     3
4  5  6  7  8  9  10
      11    12
13 14 15 16 17 18 19
      20    21
      22    23
*/

int path[100], q[25];

// 8 中操作对应的数的编号
int op[8][7] = {
    {0, 2, 6, 11, 15, 20, 22},
    {1, 3, 8, 12, 17, 21, 23},
    {10, 9, 8, 7, 6, 5, 4},
    {19, 18, 17, 16, 15, 14, 13},
    {23, 21, 17, 12, 8, 3, 1},
    {22, 20, 15, 11, 6, 2, 0},
    {13, 14, 15, 16, 17, 18, 19},
    {4, 5, 6, 7, 8, 9, 10}
};
// 8 种操作对应的逆操作的编号
int aop[8] = {5, 4, 7, 6, 1, 0, 3, 2};
// 中间 8 个数的编号
int centre[8] = {6, 7, 8, 11, 12, 15, 16, 17};

int f()
{
    int sum[4] = {0};
    memset(sum, 0, sizeof sum);
    for (int i = 0; i < 8; i ++ ) sum[q[centre[i]]] ++ ;
    // 找到中间 8 个数出现次数最多的数
    int cnt = 0;
    for (int i = 1; i <= 3; i ++ ) cnt = max(cnt, sum[i]);
    return 8 - cnt;
}

void operate(int x)
{
    int t = q[op[x][0]];
    for (int i = 0; i < 6; i ++ ) q[op[x][i]] = q[op[x][i + 1]];
    q[op[x][6]] = t;
}

bool dfs(int u, int depth, int last)
{
    if (u + f() > depth) return false;
    if (!f()) return true;

    for (int i = 0; i < 8; i ++ )
        if (last != aop[i])  // 排除逆操作
        {
            operate(i);
            path[u] = i;
            if (dfs(u + 1, depth, i)) return true;
            operate(aop[i]);
        }
    return false;
}