A-star 算法
贡献者: 有机物
A-star 算法的使用场景和双向 BFS 的差不多,都是如果在一个搜索空间非常大的情况下,可能会遍历非常多无需遍历的状态,导致时间效率非常低。由此可以使用 A* 算法。
A* 算法是在优先队列 BFS 的基础上进行优化的,我们新加了一个启发函数的概念,这样就可以优化搜索空间,降低时间复杂度。这个启发函数一般在 A* 算法上是设计了一个估价函数,在普通的优先队列 BFS 中,每次只会弹出距离当前点比较小点的临点进行更新,不会考虑未来怎么更新,有可能存在一条距离当前点权值比较大的点,但到未来的点的代价可能很小的点。
所以可以添加一个可以对未来的代价进行预估的估价函数,具体地讲,在求最短路的时候,可以存:从起点走到当前点的真实距离,以及从当前点走到终点的估计距离这两个值,在优先队列中使用 “当前距离+预估距离” 进行扩展,实际意义为当前这条路径到终点的距离。这里的优先队列为小根堆。
A* 算法算法的框架:
while (!q.empty())
{
t <--- 取出优先队列(小根堆)的队头
当终点第一次出队时,找到了答案,退出循环
for (枚举 t 的所有出边)
扩展、将临边入队
}
当估计距离为 $0$ 时,A* 算法算法变为 Dijkstra。
使用 A* 算法的前提:
设当前状态为 $\texttt{state}$,从起点到当前点的实际距离为 $\texttt{d(state)}$。
- 从起点到终点的实际距离为 $\texttt{g(state)}$,从起点到终点的估价距离为 $\texttt{f(state)}$。
- 需要满足 $\texttt{f(state)} \leq \texttt{g(state)}$。
只要满足了这个前提,使用 A* 算法,当终点第一次出队的时候,它的最小值就一定是正确的。简单的证明一下,使用反证法。
证明:
假设终点第一次出队时不是最小值。那么此时的 $\texttt{dist}$ 一定严格大于 $\tt d_{\text{最优}}$,此时最优路径中一定存在一个点 $u$,那么存在 $d_u + f_u \leq d_u + g_u = d_{\text{最优}}$。所以 $\texttt{dist} > \tt d_{\text{最优}} \geq d_u + f_u$。此时 $d_u + f_u$ 是一定严格小于终点第一次出队的距离 $\tt dist$ 的,又因为是小根堆,队列中存在一个比已经出队的更新的一个元素,矛盾。
证毕。
性质:A* 算法只能保证终点第一次出队的时候是最小值,并不能保证其他点第一次出队是最小值,并且每个点不一定会扩展(入队)一次。
证明:
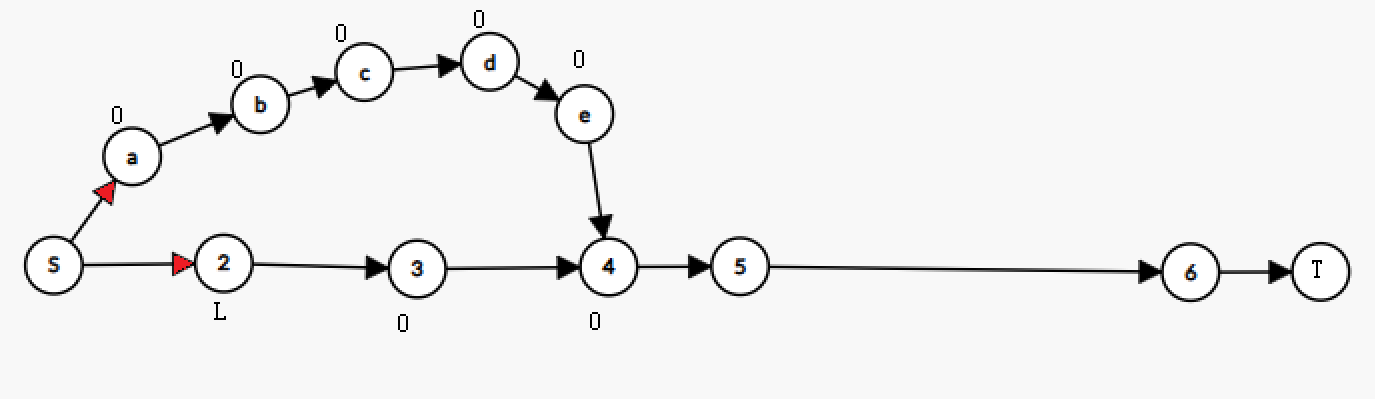
首先假设 $2$ 号点估计距离为 $L$ 为一个很大的数,其他点的估计距离为 $0$,首先从起点开始扩展,因为 $a$ 号点的估计距离加实际距离为 $1$,小于扩展到 $2$ 号点的 $L + 1$,所以会从 $a$ 点开始扩展一直扩展到 $4$ 号点,此时 $4$ 号点的距离为 $6$(从 $a$ 号点开始扩展的,所以会将 $4$ 号点从队列中弹出开始扩展 $5$ 号点,但实际是,从 $2$ 号点开始走到 $4$ 号点的距离这条路径为 $4$,这就证明了上述第一个性质。那 A* 算法是从什么时候发现走错了并且重新走呢?A* 算法有可能会走到 $6$ 号点发现此时距离为 $L + 1$ 了,走到终点为 $L + 2$,此时就发现走错了,就会重新走,可以发现 $4$ 号点在错误的路径上被扩展了一,在重新走之前的道路上被扩展了一次,所以也证明了每个点不一定会被扩展一次。
证毕。
例题:八数码。
本题不一定保证题目有解,但 A* 算法还有一个前提是一定要保证有解,不然速度还不如普通 BFS,本题有解的一个条件是:存在一个解,当且仅当不存在奇数逆序对。
所以在做之前,统计一下整个棋盘的逆序对,如果为奇数则无解。
那估价函数怎么设计呢?不难看出,每次移动只能把一个数字向目标移动一格,与目标状态越来越,即使每一步都有意义,当前状态的棋盘到目标状态的移动步数都不可能小于当前棋盘每个数字到目标棋盘的数字的曼哈顿距离之和。
所以,对于当前状态 $\texttt{state}$,可以将估价函数设计为到目标状态 $\texttt{end}$ 每个数字位置的曼哈顿距离之和。
$f(\texttt{state}) = \sum^9_{i = 1}(|\texttt{state}_{x_{i}} - \texttt{end}_{x_{i}}| + |\texttt{state}_{y_{i}} - \texttt{end}_{y_{i}}|)$。
具体细节看代码:
#define pis pair<int, string>
#define x first
#define y second
// 估价函数
int f(string state)
{
int res = 0;
for (int i = 0; i < state.size(); i ++ )
if (state[i] != 'x')
{
// 下标转移为从 0 开始
int t = state[i] - '1';
// 每个数字的当前位置与目标位置的曼哈顿距离之和
res += abs(i / 3 - t / 3) + abs(i % 3 - t % 3);
}
return res;
}
string bfs(string st)
{
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
string end = "12345678x";
char op[4] = {'u', 'r', 'd', 'l'};
unordered_map<string, int> dist; // 距离
unordered_map<string, pair<char, string>> pre; // 一个状态由哪个状态转移得来
priority_queue<pis, vector<pis>, greater<pis>> heap; // 小根堆
heap.push({f(st), st});
dist[st] = 0;
while (heap.size())
{
auto t = heap.top();
heap.pop();
string s = t.y;
if (s == end) break;
// 将当前状态 x 的位置由一维下标转移为二维
int k = t.y.find('x'), x = k / 3, y = k % 3;
string tmp = s; // 保存一下当前状态,之后用这个状态进行转移
for (int i = 0; i < 4; i ++ )
{
int a = x + dx[i], b = y + dy[i];
if (a < 0 || a >= 3 || b < 0 || b >= 3) continue;
// 一个状态可以转移为其他 4 个状态,在转移完一个状态后,要恢复之前的状态
swap(s[x * 3 + y], s[a * 3 + b]);
if (!dist.count(s) || dist[s] > dist[tmp] + 1)
{
// s 由 tmp 转移得来,操作为 op[i]
pre[s] = {op[i], tmp};
dist[s] = dist[tmp] + 1;
heap.push({f(s) + dist[s], s});
}
swap(s[x * 3 + y], s[a * 3 + b]); // 恢复
}
}
// 从最后一个状态往前推
string res;
while (end != st)
{
res += pre[end].x;
// cout << end << ' ' << pre[end].y << endl;
end = pre[end].y;
}
// 由于是从后往前推,所以答案需要反转一下
reverse(res.begin(), res.end());
return res;
}
int main()
{
string st, seq;
char c;
while (cin >> c)
{
st += c;
if (c != 'x') seq += c;
}
// 统计逆序对的数量,为奇数则无解
int cnt = 0;
for (int i = 0; i < seq.size(); i ++ )
for (int j = i; j < seq.size(); j ++ )
if (seq[i] > seq[j])
cnt ++ ;
if (cnt & 1) puts("unsolvable");
else cout << bfs(st) << endl;
return 0;
}
例题二:第 $K$ 短路。
题意:给定一张 $N$ 个点(编号 $1,2,...,N$),$M$ 条边的有向图,求从起点 $S$ 到终点 $T$ 的第 $K$ 短路的长度,路径允许重复经过点或边。
注意:每条最短路中至少要包含一条边。
题目要求第 $K$ 短路,为了能枚举到所有的路线,所以在做的时候要将所有能扩展的边全都扩展到堆中,不论距离变大还是变小,所以搜索空间非常庞大,因此可以用 A* 算法进行优化。
估价函数设计为当前点到终点的最短距离,因为无论怎么走,当前点走到终点的距离一定大于等于最短距离。
前面证明了当终点第一次从堆中弹出的时候,它的最小值就已经确定了。那么显然弹第 $K$ 次也一定是最小的。简单的来证明一下,假设第二次弹出来的值不是最小的,那么当前的最小距离一定小于最优路径,假设最优路径中存在一点 $v$,那么从起点到 $v$ 的真实距离加从 $v$ 到终点最小距离(估价距离)也一定小于等于从队列中弹出来点的距离。由于是小根堆,一定会弹出最小值,所以就矛盾了。由此证明出了当终点出队 $K$ 次的时候,它的第 $K$ 短路就确定了。
所以做法为:先建一个反图,求出从终点 $T$ 到每个点的最短距离作为估价函数。然后在 A* 算法中将能扩展到的点都加入优先队列,统计终点 $T$ 出队的次数,若出队次数等于 $K$,则直接返回当前的真实距离。
又因为每条最短路径中至少要包含一条边,所以当 $S == T$ 时,$K$ 要加一。
时间复杂度:$\mathcal{O}(nk \log_2 n)$。
C++ 代码:
const int N = 1010, M = 200010, inf = 0x3f3f3f3f;
int n, m, S, T, K, h[N], rh[N], e[M], ne[M], w[M], idx;
int dist[N], st[N]; // dijkstra, dist[i] 为点 i 的估价函数
void add(int h[], int a, int b, int c)
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
// 求出从终点 T 到其他所有点的最短路径,作为估价函数
void dijkstra()
{
memset(dist, 0x3f, sizeof dist);
dist[T] = 0;
priority_queue<pii, vector<pii>, greater<pii>> heap;
heap.push({0, T});
while (heap.size())
{
auto t = heap.top();
heap.pop();
int ver = t.second;
if (st[ver]) continue;
st[ver] = true;
for (int i = rh[ver]; ~i; i = ne[i])
{
int j = e[i];
if (dist[j] > dist[ver] + w[i])
{
dist[j] = dist[ver] + w[i];
heap.push({dist[j], j});
}
}
}
}
int Astar()
{
// heap.first 为估价函数,heap.second.first 为真实距离,heap.second.second 为当前点的编号
priority_queue<piii, vector<piii>, greater<piii>> heap;
heap.push({dist[S], {0, S}});
if (dist[S] == inf) return -1; // 判断无解的情况
int cnt = 0;
while (heap.size())
{
auto t = heap.top();
heap.pop();
int ver = t.second.second, distance = t.second.first;
if (ver == T) cnt ++ ; // 统计 T 出队的次数
if (cnt == K) return distance; // 如果 T 出队了 K 次,就找到了第 K 短路
for (int i = h[ver]; ~i; i = ne[i])
{
int j = e[i], D = distance + w[i];
heap.push({D + dist[j], {D, j}}); // 将能扩展的点都加入堆中
}
}
return -1;
}
int main()
{
cin >> n >> m;
memset(h, -1, sizeof h);
memset(rh, -1, sizeof rh);
while (m -- )
{
int a, b, c;
cin >> a >> b >> c;
add(h, a, b, c), add(rh, b, a, c);
}
cin >> S >> T >> K;
if (S == T) K ++ ; // 最短路中至少包含一条边
dijkstra();
cout << Astar() << endl;
return 0;
}