树状数组

贡献者：有机物

1. 基本原理

　　若想实现一下两种操作：

求一个区间内所有元素的和；
修改某个元素的值。

　　看到求一段序列的和很容易想到前缀和算法，单次查询的时间复杂度为 $\mathcal{O}(1)$，但是修改某个元素的值会影响前缀和数组，最坏为 $\mathcal{O}(n)$。若用普通数组，求一段数的和为 $\mathcal{O}(n)$，修改某个数为 $\mathcal{O}(1)$。若有 $m$ 次询问，两种做法的全局最坏时间复杂度都为 $\mathcal{O}(n \times m)$。树状数组这两种的操作的时间复杂度即不太慢又不太快，单次查询和修改时间复杂度都为 $\mathcal{O}(\log_2 n)$。

　　树状数组的基本思想来源于二进制拆分优化。对于一个正整数 $x$，它的二进制表示为 $a_{k - 1}, a_{k - 2}, \cdots , a_1, a_0$。可以将 $x$ 用二进制为 $1$ 的位表示出来，$x = 2^{i_1} + 2^{i_2} + \cdots + 2^{i_{k - 1}} + 2^{i_k}$。

　　其中 $i_1 > i_2 > \cdots > i_k$，可以将 $x$ 划分为 $\mathcal{O}(\left\lceil \log_2 x \right\rceil)$ 个区间。

长度为 $2^{i_k}$ 的区间 $[x - 2^{i_k} + 1 , x]$；
长度为 $2^{i_{k - 1}}$ 的区间 $[x - 2^{i_k} - 2^{i_{k - 1}} + 1, x - 2^{i_k}]$；
长度为 $2^{i_{k - 2}}$ 的区间 $[x - 2^{i_k} - 2^{i_{k - 1}} -2^{i_{k - 2}} + 1, x - 2^{i_k} - 2^{i_{k - 1}}]$；
$\cdots$
长度为 $2^{i_{1}}$ 的区间 $[x - 2^{i_k} - 2^{i_{k - 1}} -2^{i_{k - 2}} - \cdots -2^{i_1} + 1, x - 2^{i_k} - 2^{i_{k - 1}} - \cdots - 2^{i_2}]$。

　　例如 $x = 7$，可以表示为 $2^2+2^1+2^0$，区间 $[1, 7]$ 可以分解成 $[1, 4]$、$[5, 6]$、$[7, 7]$ 三个区间。长度分别为 $2^2$、$2^1$、$2^0$。将这三个区间分别用二进制表示出来 $[1, 4] = [(1, 100)_2]$、$[5, 6] = [(101, 110)_2]$、$[7, 7] = [(111, 111)]$。可以发现每个区间的长度就是每个区间的右端点二进制表示下最后一位 $1$ 及其后边的所有的 $0$。就拿 $[5, 6]$ 这个区间举例，二进制表示下右端点为 $(110)_2$，最后一位 $1$ 及后面的所有的 $0$ 就是 $(10)_2 = (2)_{10}$，其区间长度正好为 $2$。

　　进而引出了 $\tt lowbit$ 操作。

　　 $\tt lowbit$ 操作就是求一个数二进制表示下最后一位 $1$ 及其后边的所有的 $0$ 的数值。

int lowbit(x)
{
    return x & -x;
}

　　拿 $(20)_{10}$ 来举例，二进制表示下为 $(10100)_2$，最后一位 $1$ 及其后边的所有的 $0$ 就是 $(100)_2$，转化为十进制后就是 $4$，所以若调用 lowbit(20)，则会返回 $4$。

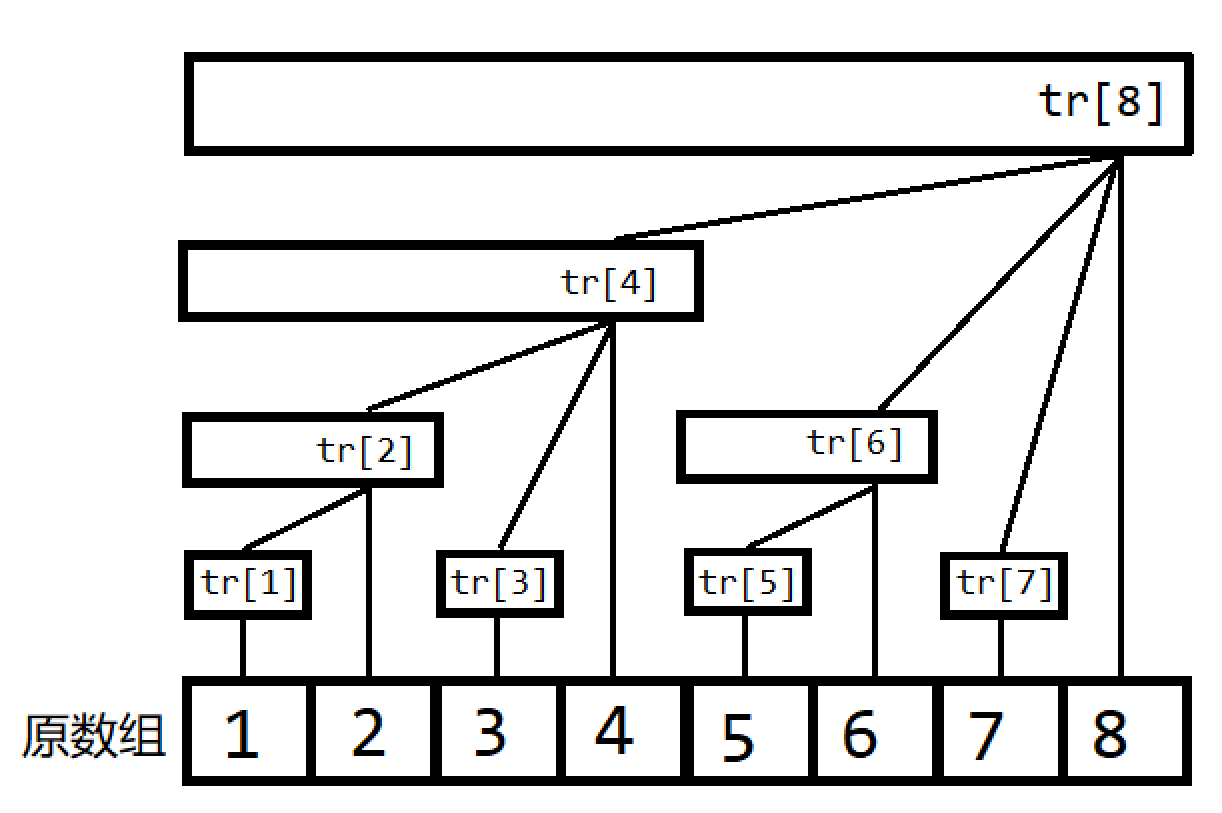
　　树状数组就是基于上述的思想的数据结构，一般是拿树状数组维护一个序列的前缀和。令 $tr_x$ 维护区间 $\texttt{[x-lowbit(x)+1, x]}$ 的和。其结构可以用下图表示出来：

图 1：树状图

　　不难看出其中具有一些性质：

若 $x$ 为奇数，则 $tr_x = a_x$，并且长度都为 $1$。
$tr_x$ 的父结点为 $\texttt{tr[x + lowbit(x)]}$。
每个节点 $x$ 的 $tr$ 数组的长度为 $\tt (lowbit(x))$。
树的深度为 $\log_2 n + 1$。

操作一：区间求和

　　例如若要计算 $[1, 7]$ 的和，则要加 $tr_7$、$tr_6$、$tr_4$。可以发现，每次将 $x$ 减去 $\tt(lowbit(x))$ 就可以找到前一个要加的结点。所以树状数组维护序列 $1 \sim x$ 代码为：

int ask(int x)
{
    int res = 0;
    for (; x; x -= lowbit(x)) res += tr[x];
    return res;
}

　　涉及到的结点最多为 $\log_2 n$，所以时间复杂度最坏为 $\mathcal{O}(\log_2 n)$。若要求 $\sum\limits^r_{i = l}a_i$，类似于前缀和，则直接输出 ask(r) - ask(l - 1)。

操作二：单点修改

　　若要将 $a_x$ 加上 $k$，则不断向上找出包含它的结点并且都加 $k$，因为每个结点维护的一个前缀的和。涉及到的结点最多为 $\log_2 n$，所以时间复杂度最坏为 $\mathcal{O}(\log_2 n)$。

void add(int x, int k)
{
    for (; x <= n; x += lowbit(x)) tr[x] += k;
}

2. 树状数组求逆序对

　　对于一个序列 $a$，若存在两个数 $i$ 和 $j$，满足 $i < j$ 且 $a_i > a_j$，则 $a_i$ 和 $a_j$ 构成逆序对。

　　普通的做法怎么计算逆序对呢？可以开一个数组 $t$，初始化全 $0$，维护 $t$ 的前缀和。然后倒序扫描整个序列，每次计算 $a_i - 1$ 的前缀和，然后将 $t_{a_i}$ 加一，因为是倒序扫描，$[1, a_i - 1]$ 的前缀和就是已经出现过的数，并且在原序列中是在 $a_i$ 后面出现的数。所以就可以求出答案。

　　举个例子：对于一个序列 $a = (3, 4, 2, 5, 1)$。

第一次循环 i = 5，a_5 = 1，前缀和为 0，将 t[1] ++。
        1 2 3 4 5 （下标）
        3 4 2 5 1
t 数组: 1

ans = 0


第二次循环 i = 4，a_4 = 5，1 ~ 4 的前缀和为 1，答案加一，t[5] ++。
        1 2 3 4 5 （下标）
        3 4 2 5 1
t 数组：1       1

ans = 1


第三次循环 i = 3, a_3 = 2, 1 ~ 1 的前缀和为 1，答案加一，将 t[2] ++。
        1 2 3 4 5 （下标）
        3 4 2 5 1
t 数组：1 1     1

ans = 1 + 1


第四次循环 i = 2, a_2 = 4, 1 ~ 3 的前缀和为 2，答案加二，将 t[4] ++。
        1 2 3 4 5 （下标）
        3 4 2 5 1
t 数组：1 1   1 1

ans = 1 + 1 + 2


第五次循环 i = 1, a_1 = 3, 1 ~ 2 的前缀和为 2，答案加二，将 t[3] ++。
        1 2 3 4 5 （下标）
        3 4 2 5 1
t 数组：1 1 1 1 1

ans = 1 + 1 + 2 + 2

所以序列 3 4 2 5 1 的逆序对的数量就为 6

　　普通做法求逆序对的操作有：求一段数的前缀和，将某个数加一，树状数组正好能做。

for (int i = n; i; i -- )
{
    ans += ask(a[i] - 1);
    add(a[i], 1);  // 相当于 t[a[i]] ++ 
}

3. 树状数组的扩展应用

　　既然树状数组支持区间查询和单点修改，那支不支持单点查询区间修改、区间查询和区间修改呢？答案是可以的，需要用到差分和前缀和的思想。

区间修改，单点查询

　　首先开一个数组 $b$，初始化为 $0$，对于将一段区间加 $x$ 的操作，就将 $b_l$ 加 $x$、$b_{r + 1}$ 减 $x$。用树状数组维护 $b$ 的前缀和，观察一下 $b$ 数组的前缀和对原数组的影响。

　　可以发现，对于 $l$ 前面的数，$b$ 的前缀和不变，$[l \sim r]$ 的数，$b$ 的前缀和加了 $x$，$r$ 后边的数，$b$ 的前缀和加了先 $x$ 又减了 $x$，相当于没变。这样 $b$ 的前缀和就成了 $a$ 数组的增量。

　　所以对于区间修改，每次只需执行 add(l, x), add(r + 1, -x)。对于单点查询，只需输出 a[x] + ask(x)。

原数组：    1 3 4 2 5
b 数组：    0 0 0 0 0

操作一：区间加：2 ~ 4 都加一

原数组：    1 3 4 2 5
b 数组：    0 1 0 0 -1

操作二：查询 a_4 的值 = a_4 + b_4 = 2 + 1 = 3
操作三：查询 a_5 的值 = a_5 + b_5 = 5 + 0 = 5

区间修改，区间查询

　　 A Simple Problem with Integers。

　　题目大意：

　　给定一个长度为 $n$ 的数列 $a$，以及 $m$ 条指令，每条指令可能是以下两种之一：

C l r d，表示把 $a[l],a[l+1], \cdots , a[r]$ 都加上 $d$。
Q l r，表示询问数列中第 $l \sim r$ 个数的和。

　　对于每个询问，输出一个整数表示答案。

　　在只有单点查询的问题中，求一遍 $b$ 数组的前缀和 $\sum\limits^x_{i=1}b_i$ 就是对 $a_x$ 的增量，则直接输出 $a_x + b_x$ 即可。

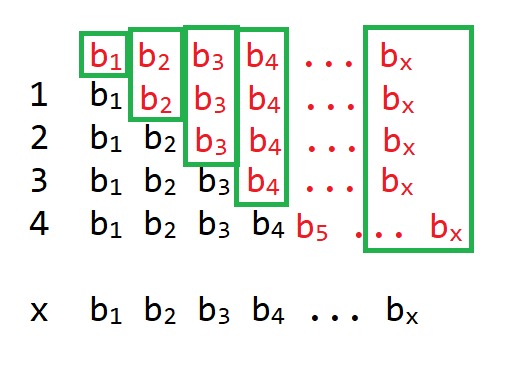
　　那么对于 $a$ 的前缀和 $a[1, x]$，$b$ 数组的增量为 $\sum\limits^x_{i=1}\sum\limits^i_{j=1}b_j$。这个式子不好用树状数组维护，可以转化为：

\begin{equation} \sum\limits^x_{i=1}\sum\limits^i_{j=1}b_j = (x + 1)\sum\limits^x_{i=1}b_i - \sum\limits^x_{i=1}i \times b_i~. \end{equation}

这个式子还可以通过图形来理解：

图 2：$\sum\limits^x_{i=1}\sum\limits^i_{j=1}b_j$

　　其中蓝色框起来的就是 $(x + 1)\sum\limits^x_{i=1}b_i$，红色字体的数为临时补的数，后续还需减去。

图 3：$(x + 1)\sum\limits^x_{i=1}b_i$

　　所以黑色字体的数就为蓝色的大框的数减去绿色的框的数，绿色的框的数正好也可以构成前缀和。

图 4：$\sum\limits^x_{i=1}i \times b_i$

　　所以本题需要维护两个前缀和，其中一个维护 $\sum\limits^x_{i=1}b_i$，另一个维护 $\sum\limits^x_{i=1}i \times b_i$。

　　所以对于每条指令，执行 $4$ 个操作。

在第一个前缀和数组中，将 $l$ 加 $x$。
在第一个前缀和数组中，将 $r+1$ 减 $x$。
在第二个前缀和数组中，将 $l$ 加 $l \times x$。
在第二个前缀和数组中，将 $r + 1$ 减 $(r + 1) \times x$。

　　对于查询操作，因为树状数组维护的是 $[1, x]$ 的和，所以先计算 $[1, r]$ 减去 $[1, l - 1]$，因为 $b$ 数组还是对数组 $a$ 的前缀和的增量，还需加上原数组 $a$ 的前缀和。

　　所以最后的式子就为： (s[r] + (r + 1) * ask(0, r) - ask(1, r)) - (s[l - 1] + l * ask(0, l - 1) - ask(1, l - 1))。

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

typedef long long LL;
const int N = 1e5 + 10;
int n, m, a[N];
LL s[N], tr[2][N];
// tr[0][x] 维护 b[1~x] 的前缀和
// tr[1][x] 维护 i * b[1~x] 的前缀和

int lowbit(int x)
{
    return x & -x;
}

LL ask(int k, int x)
{
    LL res = 0;
    for (; x; x -= lowbit(x)) res += tr[k][x];
    return res;
}

void add(int k, int x, int y)
{
    for (; x <= n; x += lowbit(x)) tr[k][x] += y;
}

int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i ++ ) cin >> a[i], s[i] = s[i - 1] + a[i];
    
    while (m -- )
    {
        string op;
        cin >> op;
        if (op == "C")
        {
            int l, r, d;
            cin >> l >> r >> d;
            add(0, l, d), add(0, r + 1, -d);
            add(1, l, l * d), add(1, r + 1, -(r + 1) * d);
        } else {
            int l, r;
            cin >> l >> r;
            cout << (s[r] + (r + 1) * ask(0, r) - ask(1, r))
            - (s[l - 1] + l * ask(0, l - 1) - ask(1, l - 1)) << endl;
        }
    }
    
    return 0;
}