贡献者: jingyuan; JierPeter; 欄、停敘; addis
- 本文处于草稿阶段。
- 正在与三角恒等式合并
未完成:合并删除相同的部分
未完成:介绍每部分的应用、推导、记忆及相关考量
未完成:超出高中范围的知识写在最后
未完成:移除原本三角恒等式的外部链接
同角的不同三角函数间的恒等关系,包括倒数关系、乘积关系以及平方关系,在三角函数时就已介绍过。他们是很重要的恒等关系,但很多时候更关注的是不同角或三角函数的不同幂次之间的关系。本文予以介绍并提供证明。注意公式很多,先了解,然后可以通过做题来记忆,本文也会提供一些方法帮助记忆。当然,过多的公式是难以记忆的,所以需要注意各个公式推导的基本条件,实际使用中,选择自己熟练的来记忆就好,剩下的公式,很多时候是可以通过熟悉的推导的,使用熟练的公式,尽管速度可能没有直接使用对应的公式容易,但不会出现混淆或错误。
1. 两角和与两角差
\begin{equation}
\sin\left(\alpha\pm \beta\right) = \sin \alpha\cos \beta \pm \cos \alpha\sin \beta~,
\end{equation}
\begin{equation}
\cos\left(\alpha\pm \beta\right) = \cos \alpha\cos \beta \mp \sin \alpha\sin \beta~,
\end{equation}
\begin{equation}
\tan\left(\alpha\pm \beta\right) = \displaystyle\frac{\tan \alpha \pm \tan \beta}{1 \mp \tan \alpha \tan \beta}~,
\end{equation}
证明
这一证法是先通过旋转法求出余弦的加法公式式 2 ,然后进行简单变换得到剩下的加法公式。思路来自П. М. Котельников的学位论文1。
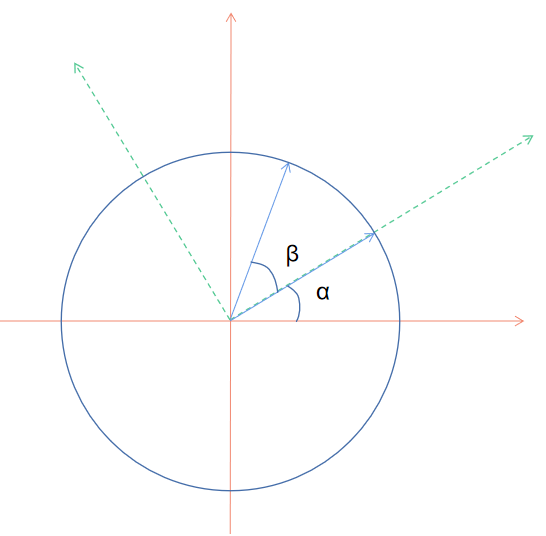
图 1:旋转法示意图。左图和右图表示的是同样的坐标系,圆都是同一个单位圆。右图中所有图形和点都围绕坐标系原点顺时针旋转了 $\beta$,从而使得 $B$ 点落在 $x$ 轴上。
如图 1 所示,在单位圆上取两个角(不一定是图示的锐角)$\alpha$ 和 $\beta$,与单位元相交得交点 $A$ 和 $B$。由于是单位圆,故可知 $A$ 的坐标为 $ \begin{pmatrix}x_A, y_A\end{pmatrix} = \begin{pmatrix}\cos\alpha, \sin\alpha\end{pmatrix} $,$B$ 的坐标为 $ \begin{pmatrix}x_B, y_B\end{pmatrix} = \begin{pmatrix}\cos\beta, \sin\beta\end{pmatrix} $。由此可计算线段 $AB$ 的长度,或者准确来说,长度的平方:
\begin{equation}
\begin{aligned}
\left\lvert AB \right\rvert ^2 =& (x_A-x_B)^2+(y_A-y_B)^2\\
=& (\cos^2\alpha+\cos^2\beta-2\cos\alpha\cos\beta)+\\&(\sin^2\alpha+\sin^2\beta-2\sin\alpha\sin\beta)\\
=& 2 \left(1-\cos\alpha\cos\beta-\sin\alpha\sin\beta \right) ~.
\end{aligned}
\end{equation}
注意这里利用了 $\cos^2x+\sin^2x=1$ 恒等式,下面也一样。
接下来,把所有点和图形都围绕坐标原点,顺时针旋转 $\beta$,得到右图。此时 $A$ 的坐标变成了 $ \begin{pmatrix}x'_A, y'_A\end{pmatrix} = \begin{pmatrix} \cos\left(\alpha-\beta\right) , \sin\left(\alpha-\beta\right) \end{pmatrix} $,$B$ 的坐标变成了 $ \begin{pmatrix}x'_B, y'_B\end{pmatrix} = \begin{pmatrix}1, 0\end{pmatrix} $。
同样地,计算线段 $AB$ 的长度平方:
\begin{equation}
\begin{aligned}
\left\lvert AB \right\rvert ^2 =& (x'_A-x'_B)^2+(y'_A-y'_B)^2\\
=& \left(\cos^2(\alpha-\beta)+1-2 \cos\left(\alpha-\beta\right) \right) +\sin^2(\alpha-\beta)\\
=& 2(1- \cos\left(\alpha-\beta\right) )~.
\end{aligned}
\end{equation}
式 4 和式 5 应相等,比较它们的最后一步即可得式 2 的减法形式,计算 $\cos\left(\alpha-(-\beta)\right)$ 即可得到加法形式。将 $\sin x= \cos\left(x-\pi/2\right) $ 代入这两个余弦加法公式,即可得到正弦加法公式式 1 。再代入 $\tan x=\sin x/\cos x$ 即可得正切的加法公式式 3 。
两角和公式
如图 1 ,要证明式 4 ,令 $OB = 1$,那么 $ \sin\left(\alpha+\beta\right) = BD = AC + BE$,而 $AC = OA \sin\alpha$,$OA = \cos\beta$;$BE = AB\cos\alpha$,$AB = \sin\beta$,代入得 $ \sin\left(\alpha+\beta\right) = \sin\alpha\cos\beta + \cos\alpha\sin\beta$。注意当 $\alpha$ 或 $\beta$ 取其他任意值时,重新画图同样可以证明该关系。所以给 $\beta$ 取相反数,就得到 $ \sin\left(\alpha-\beta\right) = \sin\alpha\cos\beta - \cos\alpha\sin\beta$
要证明式 5 ,$ \cos\left(\alpha+\beta\right) = OD = OC - EA$,而 $OC = OA\cos\alpha$,$OA = \cos\beta$;$EA = AB\sin\alpha$,$AB = \sin\beta$,代入得 $ \cos\left(\alpha+\beta\right) = \cos\alpha\cos\beta - \sin\alpha\sin\beta$,$\beta$ 取相反数得 $ \cos\left(\alpha-\beta\right) = \cos\alpha\cos\beta + \sin\alpha\sin\beta$。证毕。
两角和公式(几何矢量)
把以上过程用几何矢量语言可以表达得更自然。令 $ \hat{\boldsymbol{\mathbf{x}}} , \hat{\boldsymbol{\mathbf{y}}} $ 分别是图 1 直角坐标的单位矢量,$OA$ 方向的单位矢量为 $ \hat{\boldsymbol{\mathbf{a}}} $,$AB$ 方向的单位矢量为 $ \hat{\boldsymbol{\mathbf{b}}} $。易得
\begin{gather}
\hat{\boldsymbol{\mathbf{a}}} = \cos\alpha\ \hat{\boldsymbol{\mathbf{x}}} + \sin\alpha\ \hat{\boldsymbol{\mathbf{y}}} ~,\\
\hat{\boldsymbol{\mathbf{b}}} = -\sin\alpha\ \hat{\boldsymbol{\mathbf{x}}} + \cos\alpha\ \hat{\boldsymbol{\mathbf{y}}} ~.
\end{gather}
同样以 $O$ 为原点,$ \hat{\boldsymbol{\mathbf{a}}} , \hat{\boldsymbol{\mathbf{b}}} $ 可以看成 $x$-$y$ 直角坐标系旋转后的坐标系中的单位矢量。令 $OB$ 矢量为 $ \hat{\boldsymbol{\mathbf{u}}} $,那么 $ \hat{\boldsymbol{\mathbf{u}}} = \cos\beta\ \hat{\boldsymbol{\mathbf{a}}} + \sin\beta\ \hat{\boldsymbol{\mathbf{b}}} $,把以上两式代入得
\begin{equation}
\hat{\boldsymbol{\mathbf{u}}} = (\cos\alpha\cos\beta - \sin\alpha\sin\beta) \hat{\boldsymbol{\mathbf{x}}} + (\sin\alpha\cos\beta + \cos\alpha\sin\beta) \hat{\boldsymbol{\mathbf{y}}} ~,
\end{equation}
这就同时证明了两个两角和公式。证毕。
2. 二倍角公式
\begin{equation}
\sin2\alpha = 2\sin\alpha \cos\alpha ~,
\end{equation}
\begin{equation}
\cos2\alpha = \cos^2\alpha - \sin^2\alpha = 1 - 2\sin^2\alpha = 2\cos^2\alpha -1~,
\end{equation}
\begin{equation}
\tan2\alpha = \frac{2\tan\alpha}{1-\tan^2\alpha}~.
\end{equation}
令式 4 中 $\beta=\alpha$ 取上号得
\begin{gather}
\sin 2\alpha = 2\sin \alpha\cos \alpha~,\\
\cos 2\alpha = \cos^2 \alpha - \sin^2 \alpha~,\\
\tan 2\alpha = \frac{2\tan \alpha}{1 - \tan^2 \alpha}~.
\end{gather}
3. 半角公式
\begin{equation}
\sin\frac{\alpha}{2} = \pm\sqrt{\frac{1-\cos\alpha}{2}}~,
\end{equation}
\begin{equation}
\cos\frac{\alpha}{2}= \pm\sqrt{\frac{1+\cos\alpha}{2}}~,
\end{equation}
\begin{equation}
\tan\frac{\alpha}{2} = \pm\sqrt{\frac{1-\cos\alpha}{1+\cos\alpha}} = \frac{\sin\alpha}{1+\cos\alpha} = \frac{1-\cos\alpha}{\sin\alpha}~.
\end{equation}
注意正负号的选择需要根据 $\alpha$ 的具体取值判断。
4. 和差化积与积化和差公式
\begin{gather}
\sin \alpha + \sin \beta = 2\sin \left(\frac{\alpha + \beta}{2} \right) \cos \left(\frac{\alpha - \beta}{2} \right) ~,\\
\sin \alpha - \sin \beta = 2\sin \left(\frac{\alpha - \beta}{2} \right) \cos \left(\frac{\alpha + \beta}{2} \right) ~,\\
\cos \alpha + \cos \beta = 2\cos \left(\frac{\alpha+\beta}{2} \right) \cos \left(\frac{\alpha-\beta}{2} \right) ~,\\
\cos \alpha - \cos \beta = -2\sin \left(\frac{\alpha+\beta}{2} \right) \sin \left(\frac{\alpha-\beta}{2} \right) ~.
\end{gather}
根据上文的和差化积公式,我们也可以直接写出积化和差公式
\begin{gather}
\sin \alpha\sin \beta = \frac12 [ \cos\left(\alpha - \beta\right) - \cos
\cos \alpha\cos \beta = \frac12 [ \cos\left(\alpha + \beta\right) + \cos\left(\alpha - \beta\right) ]~,\\
\sin \alpha\cos \beta = \frac12 [ \sin\left(\alpha + \beta\right) + \sin\left(\alpha - \beta\right) ]~.
\end{gather}
证明
以式 17 为例,$\cos \alpha, \cos \beta$ 和 $\cos \alpha + \cos \beta$ 分别等于图 2 中矢量 $ \boldsymbol{\mathbf{A}} , \boldsymbol{\mathbf{B}} $(令它们的模长为 1)和 $ \boldsymbol{\mathbf{A}} + \boldsymbol{\mathbf{B}} $ 在水平方向的投影长度,而 $ \boldsymbol{\mathbf{A}} + \boldsymbol{\mathbf{B}} $ 在水平方向的投影长度等为 $ \left\lvert \boldsymbol{\mathbf{A}} + \boldsymbol{\mathbf{B}} \right\rvert \cos[(\alpha+\beta)/2]$,其中 $ \left\lvert \boldsymbol{\mathbf{A}} + \boldsymbol{\mathbf{B}} \right\rvert = 2\cos [(\beta-\alpha)/2]$,代入可得式 17 。利用 $ \boldsymbol{\mathbf{A}} + \boldsymbol{\mathbf{B}} $ 在竖直方向的投影可得式 15 ,把式 15 和式 17 中的 $\beta$ 分别替换成 $-\beta$ 和 $\beta+\pi$ 可推导出式 16 和式 18 。
5. 升幂公式
\begin{equation}
\cos2\alpha + 1 = 2\cos^2\alpha~,
\end{equation}
\begin{equation}
1-\cos2\alpha = 2\sin^2\alpha~.
\end{equation}
6. 降幂公式
\begin{equation}
\cos\alpha = \pm\sqrt{\frac{1+\cos2\alpha}{2}}~,
\end{equation}
\begin{equation}
\sin\alpha = \pm\sqrt{\frac{1-\cos2\alpha}{2}}~.
\end{equation}
7. 万能公式
\begin{equation}
\sin2\alpha = \frac{2\sin\alpha \cos\alpha}{\sin^2\alpha + \cos^2\alpha} = \frac{2\tan\alpha}{1+\tan^2\alpha}~,
\end{equation}
\begin{equation}
\cos2\alpha = \frac{\cos^2\alpha-\sin^2\alpha}{\sin^2\alpha+\cos^2\alpha} = \frac{1-\tan^2\alpha}{1+\tan^2\alpha}~.
\end{equation}
8. 辅助角公式
\begin{equation}
a\sin\alpha + b\cos\alpha = \sqrt{a^2+b^2} \sin\left(\alpha + \phi\right) ~.
\end{equation}
注:$\tan\phi = \frac{b}{a}$
证明辅助角公式
\begin{equation}
a\sin \alpha + b\cos \alpha = \sqrt{a^2+b^2} \sin\left(\alpha + \phi\right) \qquad \left(\phi = \tan^{-1}\frac{b}{a} \right) ~.
\end{equation}
9. 证明
可参考与本节内容相似的子节 1 。
两角和与两角差(旋转法)
两角和与两角差(几何矢量证法)
图 2:图示
设 $\alpha$、$\beta$ 对应的单位向量分别为 $a(\cos\alpha,\sin\alpha)$、$b( \cos\left(\alpha+\beta\right) , \sin\left(\alpha+\beta\right) )~.$
设 $a$ 与其垂直的单位向量 $m(-\sin\alpha,\cos\alpha)$ 为基向量,则
\begin{equation}
\begin{aligned}
b &= \cos\beta \cdot a + \sin\beta \cdot m \\
&= (\cos\beta \cos\alpha,\cos\beta \sin\alpha) + (-\sin\beta \sin\alpha,\sin\beta \cos\alpha) \\
&= (\cos\alpha \cos\beta-\sin\alpha \sin\beta,\sin\alpha \cos\beta + \cos\alpha \sin\beta)~.
\end{aligned}
\end{equation}
由此可得
\begin{equation}
\sin\left(\alpha+\beta\right) = \sin\alpha \cos\beta + \cos\alpha \sin\beta~,
\end{equation}
\begin{equation}
\cos\left(\alpha+\beta\right) = \cos\alpha \cos\beta - \sin\alpha \sin\beta~.
\end{equation}
用 $-\beta$ 代换 $\beta$,可得
\begin{equation}
\begin{aligned}
\sin\left(\alpha-\beta\right) &= \sin\alpha \cos\left(-\beta\right) + \cos\alpha \sin\left(-\beta\right) \\
&=\sin\alpha \cos\beta - \cos\alpha \sin\beta~,
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
\cos\left(\alpha-\beta\right) &= \cos\alpha \cos\left(-\beta\right) + \sin\alpha \sin\left(-\beta\right) \\
&=\cos\alpha \cos\beta + \sin\alpha \sin\beta~.
\end{aligned}
\end{equation}
由 $\tan\alpha = \frac{\sin\alpha}{\cos\alpha}$,得
\begin{equation}
\tan\left(\alpha+\beta\right) = \frac{\sin\alpha \cos\beta + \cos\alpha \sin\beta}{\cos\alpha \cos\beta - \sin\alpha \sin\beta}~.
\end{equation}
上下同除 $\cos\alpha\cos\beta$,得
\begin{equation}
\tan\left(\alpha+\beta\right) = \frac{\tan\alpha+\tan\beta}{1 - \tan\alpha\tan\beta}~.
\end{equation}
同理,可得
\begin{equation}
\tan\left(\alpha-\beta\right) = \frac{\tan\alpha - \tan\beta}{1 + \tan\alpha\tan\beta}~.
\end{equation}
二倍角公式
在两角和公式中,令 $\alpha = \beta$
\begin{equation}
\sin2\alpha = \sin\alpha \cos\alpha+\cos\alpha \sin\alpha = 2\sin\alpha \cos\alpha~,
\end{equation}
\begin{equation}
\cos2\alpha = \cos^2\alpha - \sin^2\alpha~,
\end{equation}
\begin{equation}
\tan2\alpha = \frac{2\tan\alpha}{1 - \tan^2\alpha}~.
\end{equation}
由 $\sin^2\alpha + \cos^2\alpha = 1$,可得
\begin{equation}
\cos^2\alpha = 1 - \sin^2\alpha~,
\end{equation}
\begin{equation}
\sin^2\alpha = 1 - \cos^2\alpha~.
\end{equation}
代入,可得
\begin{equation}
\cos2\alpha = 1 - \sin^2 - \sin^2 = 1 - 2\sin^2\alpha~,
\end{equation}
\begin{equation}
\cos2\alpha = \cos^2\alpha - (1 - cos^2\alpha) = 2\cos^2\alpha - 1~.
\end{equation}
半角公式
由余弦的二倍角公式,可得
\begin{equation}
2\sin^2\alpha = 1 - \cos2\alpha~,
\end{equation}
\begin{equation}
2\cos^2\alpha = 1 + \cos2\alpha~.
\end{equation}
用 $\frac{\alpha}{2}$ 代还 $\alpha$,可得
\begin{equation}
\begin{aligned}
2\sin^2\frac{\alpha}{2} &= 1 - \cos\alpha~,\\
\sin\frac{\alpha}{2}&= \pm\sqrt{\frac{1-\cos\alpha}{2}}~.
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
2\cos^2\frac{\alpha}{2} &= 1 + \cos\alpha~,\\
\cos\frac{\alpha}{2} &= \pm\sqrt{\frac{1+\cos\alpha}{2}}~.
\end{aligned}
\end{equation}
降幂公式
结合 $\sin 2\alpha = 2\sin \alpha\cos \alpha$ 和 $\sin^2 \alpha + \cos^2 \alpha = 1$ 可以得到
\begin{gather}
\sin^2 \alpha = \frac12 (1- \cos 2\alpha) ~, \\
\cos^2 \alpha = \frac12 (1+\cos 2\alpha)~.
\end{gather}
由此可得半角公式
\begin{gather}
\sin\frac{ \alpha}{2} = \pm\sqrt{\frac{1-\cos \alpha}{2}}~,\\
\cos\frac{ \alpha}{2}= \pm\sqrt{\frac{1+\cos \alpha}{2}}~,\\
\tan\frac{ \alpha}{2} = \pm\sqrt{\frac{1-\cos \alpha}{1+\cos \alpha}} = \frac{\sin \alpha}{1+\cos \alpha} = \frac{1-\cos \alpha}{\sin \alpha}~.
\end{gather}
注意正负号的选择需要根据 $\alpha$ 所在的区间判断,如果需要恒等式则两边取平方。
1. ^ 据刘培杰工作室出版的《世界著名三角学经典著作钩沉 平面三角卷 I》第 22 节。笔者按此名字搜索,并未找到出处,特此声明。