华东师范大学 2014 年考研物理考试试题
贡献者: 待更新
声明:“该内容来源于网络公开资料,不保证真实性,如有侵权请联系管理员”
普适气体常量 $R=8.31J(mol.K)$
波尔拉曼常 $k=1.38*10^{-22} J/K$
电子质量 $m_t=9.11*10^{-38}kg$
真空介电常量 $\varepsilon_0=8.85*10^{-12}C^2.N^{-3}.m^{-2}$
普朗克常量 $h=6.63*10^{-36}J.s$
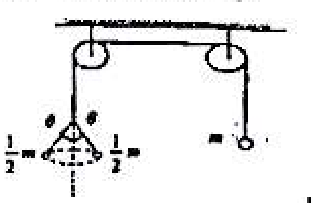
- 绳子通过两个定滑轮,右端挂质量为 m 的小球,左端挂有两个质量 $m_1=m/2$ 的小球,将右边小球约束,使之不动。使左边两小球绕竖直轴对称匀速地旋转,如图所示,则去掉约束时,右边的小球将:$(\quad)$
(A)向上运动
(B)向下运动
(C)保持不动
(D)饶滑轮摆动图 1 - 一炮弹由于特殊原因在水平飞行过程中,突然炸裂成两块,其中一块作自由下落,则另一块着地点(飞行过程中阻力不计)$(\quad)$
(A)比原来更远
(B)比原来更近
(C)仍和原来一样远
(D)条件不足,不能判定 - 质量为 $m$ 的小孩站在半径为 $R$ 的水平平台边缘上,平台可以绕通过其中心的竖立光滑固定轴自由转动,转动惯量为 $J$。平台和小孩开始时均静止。当小孩突然以相对于地面为 $v$ 的速率在台边缘沿逆时针转向走动时,则此平台相对地面旋转的角速度和旋转方向分别为 $(\quad)$
(A) $\omega=\frac{mR^2}{J}(\frac{v}{R})$,顺时针 (B) $\omega=\frac{mR^2}{J}(\frac{v}{R})$,逆时针 (C) $\omega=\frac{mR^2}{J+mR^2}(\frac{v}{R})$,顺时针 (D) $\omega=\frac{mR^2}{J+mR^2}(\frac{v}{R})$,逆时针 - 将细绳绕在一个具有水平光滑轴的飞轮边缘上,现在在绳端挂一质量为 $m$ 的重物,飞轮的角加速为 a,如果以拉力 $2mg$ 代替重物拉绳时,飞轮的角加速度将 $(\quad)$
(A)小于 a
(B)大小 a,小于 2a
(C)大于 2a
(D)等于 2a
- 一电子的总能量为 $5.0MeV$,则该电子的运动速率、动能和动量分别为(电子的静质量为 $9.1*10^8kg,leV=1.6*10^{-10}J,c=3*10^8$ 代表光速)
(A)$0.995c,4.488 MeV,2.66*10^{41}kg.m.s^{-1}$ (B)$0.995c,0.512 MeV,2.66*10^{41}kg.m.s^{-1}$ (C)$0.995c,8.96*10^{-15},2.66*10^{32}kg.m.s^{-1}$ (D)$0.995c,8.96*10^{-15},2.72*10^{28}kg.m.s^{-1}$ - 在宇宙飞船上的人从飞船后面向前面的靶子发射一颗高速子弹,此人测得离靶子的距离为 60m,子弹的速度 0.8c,求当飞船对地球以 0.6c 的速度运动时,地球上的观察者测得子弹飞行的时间分别为 $(\quad)$
(A)$25$X$10^{-7}$s
(B)$2$X$10^{-7}$s
(C)$3.125$X$10^{-7}$s
(D)$4.63$X$10^{-5}$ - 一个质量为 $m$ 的质点,仅受到力 $\vec F=k\vec r/r^3$ 的作用,式中 K 为常量,$\vec r$ 为从某一定点到质点的矢径,该质点在 $r=r_B$ 处被释放,由静止开始运动,当它到达无穷远时的速率为:$(\quad)$
(A)$\displaystyle v=\frac{2k}{mr_0}$
(B)$\displaystyle v=\sqrt{\frac{2k}{mr_0}}$
(C) $\displaystyle v=\frac{k}{mr_0}$
(D)$\displaystyle v=\frac{2k}{m}\ln r_0$ - 一长为 l,质量均匀的链条,放在光滑的水平桌面上,若使其长度的一半悬于桌边下,然后由静止释放,任其滑动,则它全部离开桌面时的速率为:$(\quad)$
(A)$\frac{1}{2}\sqrt{3gl}$
(B)$\sqrt{\frac{3}{2}gl}$
(C)$\sqrt{\frac{3}{2}}gl$
(D)$\frac{\sqrt{3}}{2}$ - 用一根细线吊一重物,重物质量为 $5kg$,重物下面再系一根同样的细线,细线只能经受 $70N$ 的拉力,现在突然向下拉一下下面的线。设力最大值为 50N,则 $(\quad)$
(A)下面的线先断
(C)两根线一起断
(B)上面的线先断
(D)两根线都不断 - 轮船在水上以相对于水的速度 $\vec v_1$ 航行,水流速度为 $\vec v_2$,一人相对于甲以速度 $\vec v_3$ 行走,如人相对于岸静止,则 $\vec v_1,\vec v_2,\vec v_3$ 的关系是 $(\quad)$
(A)$\vec v_1+\vec v_2=\vec v_3$
(B)$\vec v_1+\vec v_3=\vec v_2$
(C)$\vec v_2+\vec v_3=\vec v_1$
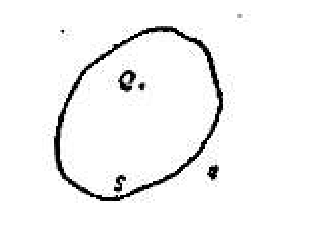
(D)$\vec v_1+\vec v_2+\vec v_3=0$ - 点电荷 $Q$ 被曲面 $S$ 所包,从无穷远处引入另一点电荷 $q$ 至曲面外
一点,如图所示,则引入前后:$(\quad)$
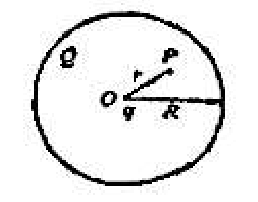
(A)通过曲面 S 的电通量不变,曲面上各点场强不变 (B)通过曲面 S 的电通量变化,曲面上各点场强不变 (C)通过曲面 S 的电通量变化,曲面上各点场强变化 (D)通过曲面 S 的电通量不变,曲面上各点场强变化图 2 - 真空中一半径为 $R$ 的球面均匀带电 $Q$,在球心 O 处有一带电量为 $q$ 的点电荷如图所示,设无穷远处为电势零点,则在球内离球心 O 距离为 $r$ 的 $P$ 点处的电势为 $(\quad)$
(A) $\displaystyle \frac{q}{4\pi \varepsilon_0 r}$
(B) $\displaystyle \frac{1}{4\pi \varepsilon_0}(\frac{q}{r}+\frac{Q}{R})$
(C) $\displaystyle \frac{q+Q}{4\pi \varepsilon_0 r}$
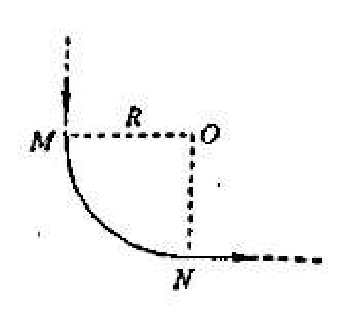
(D) $\displaystyle\frac{1}{4\pi \varepsilon_0}(\frac{q}{r}+\frac{Q-q}{R})$图 3 - 一无限长载流导线,在中部弯成如图所示的四分之一圆周 MN,圆心为 O,半径为 R,则在 O 点处的磁感应强度 B 的大小为 $(\quad)$
(A)$\displaystyle \frac{\mu_0 I}{2\pi R} $
(B)$\displaystyle \frac{\mu_0 I}{2\pi R}(I+\frac{\pi}{4})$
(C)$\displaystyle \frac{\mu_0 I}{8 \pi R}$
(D)$\displaystyle \frac{\mu_0 I}{8R}$图 4 - 一个介质球壳相对介电常数为 $\varepsilon_r$。,其内半径为 R。外半径为 $R+a$,在球心有一电量为 $q_0$ 的点电荷,对于 $R< r< R+a$ 电场强度为 $(\quad)$
(A) $\displaystyle \frac{q_0}{4\pi \varepsilon_0 \varepsilon_r r^2}$
(B)$\displaystyle \frac{q_0}{4\pi \varepsilon_0 r^2}$
(C)$\displaystyle \frac{q_0}{4\pi \varepsilon_r r^2}$
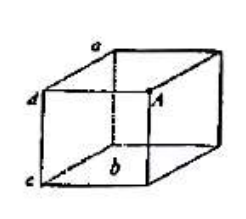
(D)$\displaystyle \frac{(\varepsilon_r-1)q_0}{4\pi \varepsilon_r r^2}$ - 如图所示,一点电荷 $q$ 位于立方体 $A$ 角上,则通过侧面 $abcd$ 的电通量为 $(\quad)$
(A) $\displaystyle \frac{1}{4} \frac{q}{\varepsilon_0}$
(B) $\displaystyle \frac{1}{6} \frac{q}{\varepsilon_0}$
(C) $\displaystyle \frac{1}{6} \frac{q}{\varepsilon_0}$
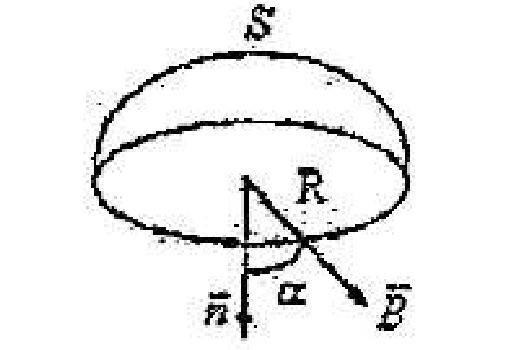
(C) $\displaystyle \frac{1}{24} \frac{q}{\varepsilon_0}$图 5 - 如图所示,在磁感应强度为 $\vec B$ 的均匀磁场中作一半径为 $R$ 的半球面 $S$,$S$ 边线所在平面的法线方向单位矢量 $\vec n$ 与 $\vec B$ 的夹角为 $\alpha$,则通过半球面 $S$ 的磁通量为 $(\quad)$
(A) $\pi R^2 B$
(B)$2pi R^2 B$
(C)$\pi R^2 B \sin \alpha$
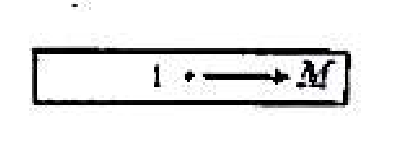
(D)$\pi R^2 B \sin \alpha$图 6 - 下图是一根沿轴向均勾磁化的细长水久磁棒,磁化强度为 $M$,图中标出的 $I$ 点的 $B$ 值是
$(\quad)$
(A)$\mu_0 M$
(B)0
(C)$\displaystyle \frac{1}{2} \mu_0 M$
(D)$\displaystyle -\frac{1}{2} \mu_0 M$图 7 - 平行板电容器充电后与电源断开。然后充满相对介电常数为 $\varepsilon_0$ 的均匀介质。则电场强度 $E$、电容 $C$ 电压 $U$、电场能量 $W$ 护四个量和充介质前相比较是 $(\quad)$
(A)$E \uparrow ,C\uparrow ,U\uparrow ,W\uparrow$
(B)$E \downarrow ,C\uparrow ,U\downarrow ,W\uparrow$
(C)$E \downarrow ,C\uparrow ,U\uparrow ,W\downarrow$
(D)$E \uparrow ,C\uparrow ,U\downarrow ,W\downarrow$
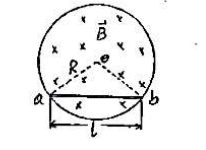
- 在一半径为 $R$ 的均匀圆柱体内充满磁感应强度为后的均匀磁场,这磁场以速率 $\frac{dB}{dt}$ 在减小,如图放置的金属棒 $ab(ab=1<2R)$ 两端的感生电动势 $\varepsilon_{ab}$ 为 $(\quad)$
(A) $\displaystyle l \sqrt{R^2-(\frac{l}{2})^2} \frac{\mathrm{d}{B}}{\mathrm{d}{t}} $,a 点电势高
(B) $\displaystyle \frac{l}{2}l \sqrt{R^2-(\frac{l}{2})^2} \frac{\mathrm{d}{B}}{\mathrm{d}{t}} $,a 点电势高
(C) $\displaystyle \frac{l}{2}l \sqrt{R^2-(\frac{l}{2})^2} \frac{\mathrm{d}{B}}{\mathrm{d}{t}} $,b 点电势高
(D) $\displaystyle l \sqrt{R^2-(\frac{l}{2})^2} \frac{\mathrm{d}{B}}{\mathrm{d}{t}} $,b 点电势高
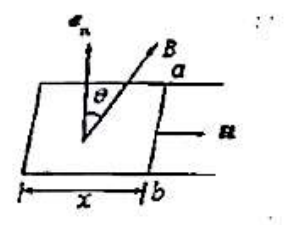
图 8 - 均匀磁场与导体回路法线 $e_a$ 的夹角为 $\theta=\pi/3$,磁感强度 $B$ 随时间按正比的规律增加,即 $B=kt(k>0)$,$ab$ 边长为 $l$,且以速度 $u$ 向右滑动(设 $t=0$ 时,$x=0$),则导体回路内任意时刻感应电动势的大小和方向为:$(\quad)$
(A)$\displaystyle 2kult$ 逆时针方向
(B)$\displaystyle \frac{1}{2kult}$ 顺时针方向
(C)$kult$ 顺时针方向
(D)$kult$ 逆时针方向图 9 - 光场中某一点的复振幅为 $-Ae^\theta/(2i)$,则该点电场震动的相位为:$(\quad)$
(A) $\theta$
(B) $\theta-\pi/2$
(C) $\theta+\pi/2$
(D)0 - 在杨氏双缝于涉实验中,将实验装置从空气中移到水中,则观测屏上:$(\quad)$
(A)条纹间距变大
(B)条纹间不变
(C)条纹间距变小
(D)条纹消失
- 用单色光垂直照射在牛顿环装置上,将其平凸透镜直地向上平移,可以观察到于涉条纹:$(\quad)$
(A)向右平移
(B)向中心收缩
(C)向外扩张
(D)静止不动向左平移
(E)向左平移 - 菲涅尔圆孔衍射中,对圆孔轴上某一参考点,衍射孔仅包含 $ 1/2$ 个半波带,现在撤掉衍射屏,点光强变为原来的 $(\quad)$
(A)1/2
(B)2 倍
(C)1/4
(D)4 倍
(E)1 倍 - 在单缝夫琅禾费衍射实验中,单色平行光沿水平方向垂直射向单缝,现将单缝向上平移一小段距
离,则观测屏上的条纹 $(\quad)$
(A)向上平移
(B)向下平移
(C)不动
(D)间距变大 - 在光栅夫琅禾费衍射实验中,单色平行光由垂直射向光栅改为斜入射光栅,观察到的光谱线 $(\quad)$
(A)最高级次变小,条数不变
(B)最高级次变大,条数不变
(C)最高级次变大,条数变多
(D)最高级次不变,条数不变 - 光栅的总缝数为 $N$,光栅常数为 $d$,则对某一级光谱而言,其分辨本领 $(\quad)$
(A)由 N 决定
(B)由 d 决定
(C)由 Nd 决定
(D)由 1/(Nd)决定 - 右旋园偏振光垂直通过 1/2 波片后,其出射光的偏振态是 $(\quad)$
(A)左旋圆偏振光
(B)右旋圆振光
(C)左旋椭圆偏振光
(D)右旋椭圆偏振光 - 三个偏振片 $P1,P2$ 与 $P3$ 堆叠在一起,$P1$ 与 $P3$ 的偏振化方向相互垂直,$P2$ 与 $P1$ 的偏振化方向夹角为 30°,强度为 $I$ 的自然光垂直入射到偏振片 $P1$,并依次透过振片 $P1,P2$ 与 $P3$,若不考虑偏振片的吸收和反射,则通过三个偏振片后的光强为 $(\quad)$
(A)I/4
(B)3I/8
(C)3I/16
(D)3I/32 - 一黑体为立方体空腔,现将空腔的边长增大一倍,而空腔及腔壁的温度降低一半,则黑体辐射的能量与原有的辐射能量之比为 $(\quad)$
(A) 4:1
(B) 1:4
(C) 1:1
(D) 1:2
(E) 2:1 - 绝对黑体具有的重要特点是 $(\quad)$
(A)不吸收电磁波
(B)不反射电磁波
(C)不辐射电磁波
(D)不辐射可见光 - 已知普朗克常数 $h=6.63$x$10^{-34}J.s$,光速 $c=3.00$x$10^8m.s^{-1}$。某带电粒子的质量是 $1.84$x$10-{-28}kg$,速度是 $2.0$x$10^4 m/s$,则该粒子的康普顿波长为 $(\quad)$
(A)$1.8$x1$0^{-12}$
(B)$1.2$x$10^{-14}$
(C)$1.8$x$10^{-18}$
(D)$4.0$x$10^{-23}$ - 根据玻尔理论可以计算氢原子光谱的 $(\quad)$
(A)强度
(B)宽度
(C)频率
(D)俯振 - 当氢原子中从第一激发态跃迁到基态时,核外电子的运动速度变成原来的 $(\quad)$
(A)1/2
(B)1/4
(C)2 倍
(D)4 倍 - 2012 年,欧洲核子研究中心发现了静止质量为 $m=2.24$x$10^{-25}kg$ 的希格斯粒子。理论预言,这种希格斯粒子的质量不确定度为 $\Delta m/m$=$1.67$x$10^{-5}$。已知普朗克常数 $h=6.63$x$10^{-34}J.s$,光速 $c=3.00$x$10^8 m/s$。根据不确定性关系可估算,该粒子的平均寿命的理论值最接近 $(\quad)$
(A)$10^{-5}$
(B)$10^{-10}$
(C)$10^{-22}$
(D)$10^{-29}$ - 下列实验现象,不需要引入电子自旋的概念就能解释的是 $(\quad)$
(A)碱金属双线
(B)施特恩-格拉赫实验
(C)正常塞曼效应
(D)反常塞曼效应 - 下列原子态符号中,错误的是 $(\quad)$
(A)$^1S_1$
(B)$^1S_{u2}$
(C)$^1p_1$
- 根据电偶极辐射跃迁的选择规则,电子组态 $1S^2$ 可以跃迁到 $(\quad)$
(A)2s2s
(B)2s2p
(C)2$p^2$
(D)3s3d - 原子系统处于正常状态时,每个电子趋向占据 $(\quad)$ 的态。
(A)主量子数最小
(B)角量子数最小
(C)自旋量子数最小
(D)能量最低 - 根据泡利原理,在 $I=2$ 的次壳层中,最多可以容纳的电子数为 $(\quad)$
(A)4
(B)8
(C)5
(D)10 - 一定量的理想气体储存于某一容器中,温度为 T,气体分子的质量为,则分子速度在 X 方向分
量的平均值为 $(\quad)$
(A)$\displaystyle \bar {v_x}=\sqrt{\frac{8kT}{\pi m}}$
(B)$\displaystyle \bar {v_x}=\frac{1}{3}\sqrt{\frac{8kT}{\pi m}}$
(C)$\displaystyle \bar {v_x}=\sqrt{\frac{8kT}{3\pi m}}$
(D)$\displaystyle \bar {v_x}=0$
- 在一封闭容器中盛有 $1mol$ 氮气(可视为理想气体),这时分子无规则运动的平均自由程仅取决于 $(\quad)$
(A)压强 P
(B)体积 V
(C)温度 T
(D)平均碰撞频率 - 物质量相同的氦气和氮气(可视为理想气体),从相的初状态(P,V,T 相同)开始做等膨胀到
同一末状态,则下列说法正确的是 $(\quad)$
(A)对外所做的功相同
(B)从外界吸收的热量相同
(C)气体分子平均速率的增量相同
(D)以上说法都不正确 - 一定量的真实气体,绝热地向真空自由膨胀,则气体 $(\quad)$
(A)温度上升
(B)温度下降
(C)温度不变
- 摩尔数相同的氢气和氨气,若它们的温度相同,则两气体 $(\quad)$
(A)内能必相等
(B)分子的平均动能相同
(C)分子的平均平动能相同
(D)分子的平均速率相同 - $1mol$ 的理想气体由最初温度 $T_1$ 绝热地影胀到最终温度 $T_2$,则气体对外所做的功为 $(\quad)$
(A)$R(T_1-T_2)$
(B)$C_v(T_1-T_2)$
(C)$C_v \ln\left(T_1-T_2\right) $
(D)$C_p(T_1-T_2)$
- 若在一个固定的容器内,理想气体分子的平均速率提高为原来的 2 倍,则有 $(\quad)$
(A)温度为原来的 2 倍,压强为原来的 4 倍
(B)温度和压强都为原来 2 倍
(C)温度为原来的 4 倍,压强为原来的 2 倍
(D)温度和压强都为原来 4 倍 - 若在某个过程中,一定量的理想气体的内能 $E$ 随压强的变化关系为一直线,则该过程为 $(\quad)$
(A)等温过程
(B)等压过程
(C)等体过程
(D)绝热过程 - 一个体积为 v 的容器,充入温度为 $T_1$ 的双原子分子的理想气体,强为 P,当器内的气体被
加热,温度开高到 $T_2$ 之后,因容器漏气而压强仍为 P,则容器内气体的内能 $(\quad)$
(A)变大
(B)变小
(C)不变
(D)无法确定 - 一定量的理想气休,起始温度为 T,体积为 v,经绝热过程后体积变为 2V,又经过等压过程后温
度回升到起始温度,最后经过等温过程回到起始状态,在此循环过程中 $(\quad)$
(A)气体从外界净吸热为负值
(B)气体对外界净做功为正值
(C)气体从外界净吸热为正值
(D)气体内能减少