牛顿运动定律（综述）

贡献者：待更新

　　（本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章）

　　牛顿运动定律是三条描述物体运动与作用于其上的力之间关系的物理定律。这些定律构成了牛顿力学的基础，可概括为以下内容：

一个物体将保持静止状态或以恒定速度沿直线运动，除非有力作用在其上。
在任一时刻，物体所受的合力等于物体的加速度乘以其质量，或等同于物体动量随时间变化的速率。
如果两个物体相互施加力，这些力的大小相等但方向相反。[1][2]

　　牛顿的三大运动定律最早由艾萨克·牛顿在他的著作《自然哲学的数学原理》（拉丁文：《Philosophiæ Naturalis Principia Mathematica》）中提出，该书首次出版于 1687 年。牛顿利用这些定律研究并解释了许多物理物体和系统的运动。自牛顿以来，新的见解，特别是关于能量的概念，基于他的基础构建了经典力学的领域。同时也发现了牛顿定律的局限性：当物体以极高的速度运动时（狭义相对论）、质量极大时（广义相对论）、或在极小尺度上（量子力学），需要新的理论来解释。

1. 前提条件

　　牛顿定律通常是以点或质点的形式表述的，即体积可以忽略不计的物体。这在实际物体中是一个合理的近似，当内部各部分的运动可以忽略不计，并且物体之间的距离远大于它们各自的大小时，牛顿定律是适用的。例如，当考虑地球围绕太阳的轨道时，可以将地球和太阳都近似为点状物体，但在考虑地球表面的活动时，地球显然不是点状物体。[注 1]

　　运动的数学描述，即运动学，是基于使用数值坐标来指定位置的概念。物体的运动通过这些数值随时间变化来表示：物体的轨迹是一个函数，它将每个时间变量的值与所有位置坐标的值关联起来。最简单的情况是一维运动，也就是当一个物体只能沿直线运动时。此时，它的位置可以用一个数值表示，说明它相对于某个选定参考点的位置。例如，一个物体可能在一条从左到右的轨道上自由滑动，因此它的位置可以通过距离某个方便的零点（原点）的距离来指定，负数表示位于左侧的位置信息，正数表示位于右侧的位置信息。如果物体的位置是时间的函数 $ s(t) $，那么物体在从 $ t_0 $ 到 $ t_1 $ 的时间间隔内的平均速度为： \[ \frac{\Delta s}{\Delta t} = \frac{s(t_1) - s(t_0)}{t_1 - t_0}~ \] 在这里，按照传统使用希腊字母 Δ（delta）表示 “变化量”。正的平均速度意味着在所讨论的时间间隔内，位置坐标 $ s $ 增加；负的平均速度表示该间隔内的位置净减少；而零的平均速度则意味着物体在时间间隔结束时与开始时位于同一位置。微积分提供了定义瞬时速度的方法，它衡量物体在某一时刻的速度和运动方向，而不是在一个时间区间内。瞬时速度的一种表示法是用符号 $ d $ 替代 $ \Delta $，例如： \[ v = \frac{ds}{dt}~ \] 这表示瞬时速度是位置随时间变化率的导数。

　　这表明瞬时速度是位置对时间的导数。大致可以理解为位置的微小变化 $ ds $ 与发生在微小时间间隔 $ dt $ 之间的比率【7】。更准确地说，速度和所有其他导数都可以通过极限的概念来定义【6】。一个函数 $ f(t) $ 在给定的输入值 $ t_0 $ 处有极限 $ L $，如果通过选择足够接近 $ t_0 $ 的输入，可以使 $ f $ 与 $ L $ 之间的差异任意小。我们写作： \[ \lim _{t\to t_{0}}f(t)=L~ \] 瞬时速度可以定义为当时间间隔趋于零时，平均速度的极限： \[ \frac{ds}{dt}=\lim _{\Delta t\to 0}\frac{s(t+\Delta t)-s(t)}{\Delta t}~ \] 加速度与速度的关系，就像速度与位置的关系一样：它是速度对时间的导数【注 2】。加速度同样可以通过极限定义： \[ a=\frac{dv}{dt}=\lim _{\Delta t\to 0}\frac{v(t+\Delta t)-v(t)}{\Delta t}~ \] 因此，加速度是位置的二阶导数，通常写作： \[ \frac{d^{2}s}{dt^{2}}~ \] 位置，当被认为是从原点的位移时，是一个向量：既有大小又有方向的量【9】：1。速度和加速度也是向量量。向量代数的数学工具提供了描述二维、三维或更多维度运动的手段。向量通常用带箭头的符号表示，如 $ \mathbf{s} $，或者用粗体字体表示，如 $ {\bf {s}} $。向量常常以箭头的形式可视化表示，向量的方向就是箭头的方向，向量的大小则由箭头的长度表示。数字上，一个向量可以用列表表示；例如，一个物体的速度向量可能是： \[ \mathbf{v} = (3 \ \mathrm{m/s}, 4 \ \mathrm{m/s})~ \] 这表示物体以每秒 3 米的速度沿水平轴运动，以每秒 4 米的速度沿垂直轴运动。在不同的坐标系中，描述相同运动时会用不同的数值表示，向量代数可以用于在这些不同的表示法之间转换【9】：4。

　　力学的研究由于一些日常用词（如 “能量”）在物理学中具有特殊的技术含义而变得复杂【10】。此外，某些在日常语言中同义的词在物理学中并非如此：例如，力与功率或压力不同，质量与重量的含义也不同【11】【12】：150。物理学中的 “力” 概念将日常的 “推” 或 “拉” 进行量化。在牛顿力学中，力通常来源于绳索、摩擦、肌肉力量、重力等。与位移、速度和加速度一样，力也是一个向量量。

2. 定律

第一定律

　　从拉丁文翻译过来，牛顿第一定律的表述是：
每个物体都保持静止状态或沿直线做匀速运动，除非有外力迫使它改变这种状态【注 3】。

　　牛顿第一定律表达了惯性原理：物体的自然行为是以恒定速度沿直线运动。物体的运动会保持现状，但外部的力可以扰动这种状态。

图 1：人造卫星沿着曲线轨道运动，而不是沿直线运动，这是由于地球的重力作用。

　　对牛顿第一定律的现代理解是：没有一个惯性观察者比另一个惯性观察者更 “特权”。惯性观察者的概念量化了日常中不感受到运动的想法。例如，一个站在地面上看火车经过的人是惯性观察者。如果地面的观察者看到火车以恒定速度沿直线平稳移动，那么坐在火车上的乘客也将是惯性观察者：乘客感觉不到运动。

　　牛顿第一定律表达的原理是，无法判断哪个惯性观察者 “真正” 在运动，哪个 “真正” 是静止的。一个观察者的静止状态对于另一个观察者来说可能是匀速直线运动状态，任何实验都无法判定哪种观点是正确或错误的。不存在绝对的静止标准【17】【14】：62–63【18】：7–9。虽然牛顿本人认为绝对的空间和时间是存在的，但他也认为实验所能测量的空间和时间都是相对的【19】。

第二定律

　　物体的运动变化与施加的力成正比，并且沿着施力的直线方向进行。[14]:114 牛顿所说的 “运动”，指的是现在称为动量的量，动量取决于物体所包含的物质量、该物体运动的速度以及它运动的方向。[20] 在现代符号中，物体的动量是其质量与速度的乘积： \[ \mathbf{p} = m \mathbf{v}~ \] 其中，质量 $m$、速度 $ \mathbf{v} $ 和动量 $ \mathbf{p} $ 三者都可以随时间变化。牛顿第二定律的现代形式表述为动量的时间导数等于力： \[ \mathbf{F} = \frac{d\mathbf{p}}{dt}~ \] 如果质量 $m$ 随时间不变，那么导数只作用在速度上，因此力等于质量与速度的时间导数之积，即加速度： \[ \mathbf{F} = m \frac{d\mathbf{v}}{dt} = m \mathbf{a}~ \] 由于加速度是位置相对于时间的二阶导数，这条定律也可以写作： \[ \mathbf{F} = m \frac{d^2 \mathbf{s}}{dt^2}~ \] 作用在物体上的力是以向量形式相加的，因此物体所受的总力不仅取决于各个力的大小，还取决于它们的方向。当物体的合力等于零时，根据牛顿第二定律，物体不会产生加速度，称之为机械平衡状态。如果在物体的位置稍微发生变化时，物体仍然保持在该平衡附近，那么这种机械平衡是稳定的。否则，平衡就是不稳定的。

图 2：一个表示斜面上物体的受力图，展示了垂直于斜面的法向力 $N$，向下的重力 $mg$，以及沿着斜面方向的力 $f$，例如由摩擦力或绳子施加的力。

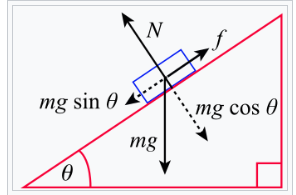
　　常见的力共同作用的视觉表示形式是受力图，它以图解的方式描绘了受关注的物体及其受到的外部力量。例如，一个坐在斜面上的方块的受力图可以展示重力、法向力、摩擦力和绳子张力的组合。[注 4]

　　牛顿第二定律有时被作为力的定义来呈现，即当惯性观察者看到一个物体加速时，说明存在一个力。为了避免这种解释成为自我证明的循环推理——加速度意味着存在力，力意味着存在加速度——必须对力做出其他的说明。例如，可以用方程来描述力，比如牛顿的万有引力定律。通过将这样的力表达式 $ \mathbf{F} $ 插入到牛顿第二定律中，就能写出一个具有预测能力的方程。[注 5] 牛顿第二定律也被认为为物理学设立了一个研究纲领，明确了该学科的重要目标是识别自然界中存在的各种力，并编制物质成分的目录。[14]: 134 [25]: 12-2

第三定律

　　每一个作用总有一个与之相反的、大小相等的反作用；或者说，两个物体之间的相互作用总是大小相等，并且方向相反。[14]:116

　　对牛顿第三定律的过于简化的表述，如 “作用等于反作用”，可能让几代学生产生了误解：作用和反作用是作用在不同物体上的。例如，考虑一本静止在桌子上的书。地球的引力向下拉动书本。对此 “作用” 的 “反作用” 并不是桌子支撑书本向上的力，而是书本对地球的引力作用。[注 6]

图 3：火箭通过火箭发动机向下产生强大的反作用力来工作，这个反作用力将火箭推向上方，而不依赖于地面或大气的存在。

　　牛顿第三定律与一个更基本的原理——动量守恒定律——有关。即使在某些情况下牛顿的表述不适用（例如，当力场和物体都携带动量时，或者在量子力学中正确定义动量时），动量守恒定律仍然成立。[注 7] 在经典力学中，如果两个物体的动量分别是 $ \mathbf{p}_1 $ 和 $ \mathbf{p}_2 $，那么这两个物体的总动量是：$\mathbf{p} = \mathbf{p}_1 + \mathbf{p}_2~$ 总动量 $ \mathbf{p} $ 的变化率为： \[ \frac{d\mathbf{p}}{dt} = \frac{d\mathbf{p}_1}{dt} + \frac{d\mathbf{p}_2}{dt}~ \] 根据牛顿第二定律，动量变化的第一个项是作用在第一个物体上的总力，第二个项是作用在第二个物体上的总力。如果这两个物体是隔离的，不受外部影响，那么第一个物体所受的唯一力只能来自第二个物体，反之亦然。根据牛顿第三定律，这些力的大小相等、方向相反，因此它们相加时会相互抵消，总动量 $ \mathbf{p} $ 保持不变。或者，若已知 $ \mathbf{p} $ 是恒定的，则可以推断出两个物体的力大小相等且方向相反。

其他可能被视为补充定律的候选法则

　　一些来源建议将经典力学中使用的其他概念提升到牛顿定律的地位。例如，在牛顿力学中，由两个较小物体组合而成的物体的总质量是其各自质量的总和。物理学家弗兰克·维尔切克（Frank Wilczek）曾建议通过称其为 “牛顿第零定律” 来强调这一假设。[33] 另一个 “第零定律” 的候选者是这样的事实：物体在任一瞬间对该瞬间施加的力作出反应。[34] 同样，力像向量一样相加（或遵守叠加原理）这一概念，以及力改变物体能量的概念，都曾被描述为 “第四定律”。[注 8]

例子

　　利用牛顿定律研究大质量物体的行为被称为牛顿力学。牛顿力学中的一些问题因其概念性或历史意义而特别值得注意。

匀加速运动

图 4：使用频闪灯以每秒 25 帧拍摄的弹跳球。在两次弹跳之间，球的高度随时间的变化接近抛物线，但由于空气阻力、旋转以及碰撞时变形为非球形，轨迹会偏离抛物线。

　　如果一个物体从静止状态开始在地球表面附近下落，那么在没有空气阻力的情况下，它将以恒定的速度加速。这称为自由落体。在自由落体过程中获得的速度与经过的时间成正比，物体所经过的距离与经过时间的平方成正比。[39] 重要的是，加速度对所有物体都是相同的，与它们的质量无关。这是结合牛顿的第二运动定律和万有引力定律得出的。后者表明地球对物体施加的引力大小为 \[ F = \frac{GMm}{r^2}~ \] 其中，$ m $ 表示下落物体的质量，$ M $ 表示地球的质量，$ G $ 是牛顿引力常数，$ r $ 是从地球中心到物体位置的距离，近似为地球的半径。将这个力等同于 $ ma $（物体的质量乘以加速度），物体的质量 $ m $ 会在方程的两边相互抵消，剩下的加速度只依赖于 $ G $、$ M $ 和 $ r $，并且 $ r $ 可以视为常数。这个特定的加速度通常用 $ g $ 表示： \[ g = \frac{GM}{r^2} \approx 9.8~\text{m/s}^2~ \] 如果物体不是从静止状态释放，而是以非零速度向上和/或水平发射，那么自由落体就变成了抛体运动。[40] 当空气阻力可以忽略时，抛体的轨迹呈抛物线形，因为重力只影响物体的垂直运动，而不影响水平运动。在抛体轨迹的最高点，物体的垂直速度为零，但其加速度始终是向下的 $ g $，这一点在任何时刻都不变。将错误的向量设为零是物理学生常见的困惑之一。[41]

匀速圆周运动

图 5：两个做匀速圆周运动的物体围绕着质心（两个物体的共同质量中心）运行。

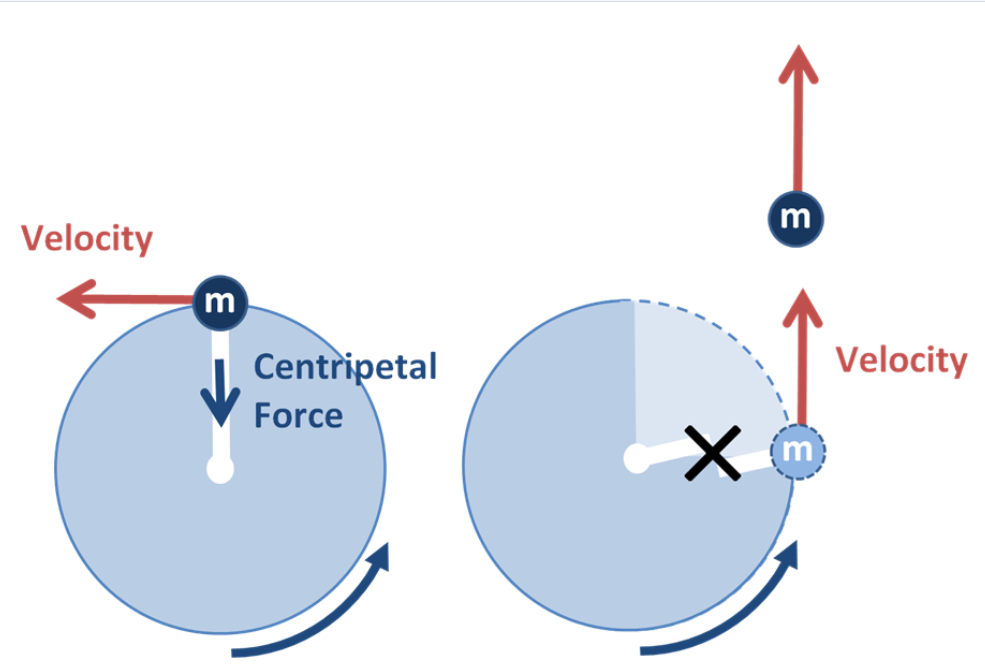
　　当一个物体做匀速圆周运动时，作用在它上的力改变了其运动方向，但不改变其速度。对于一个以恒定速度 $ v $ 在半径为 $ r $ 的圆周上运动的物体，其加速度的大小为 \[ a = \frac{v^2}{r}~ \] 并指向圆心。[注 9] 为维持这种加速度所需的力，称为向心力，因此它也指向圆心，大小为 $mv^2/r$ 许多轨道运动，例如月球绕地球的运动，可以近似为匀速圆周运动。在这种情况下，向心力是引力，根据牛顿的万有引力定律，其大小为 $GMm/r^2$ 其中 $ M $ 是被绕行的较大物体的质量。因此，可以通过观测一个物体绕另一个物体的轨道运动来计算该物体的质量。[43]:130

　　牛顿的炮弹是一个介于抛体运动和匀速圆周运动之间的思想实验。一颗炮弹如果从高悬崖边上以较小的力量抛出，它落地的时间与静止状态下掉落的时间相同，因为重力只影响炮弹在垂直方向上的动量，水平运动并不会削弱重力的影响。如果炮弹以更大的初始水平速度发射，它在落地前会飞得更远，但仍会在相同的时间内落地。然而，如果炮弹以更大的初始速度发射，地球的曲率将变得显著：地面本身会向远离炮弹的方向弯曲。一颗非常快速的炮弹将以与地球弯曲的速率偏离惯性直线轨迹；换句话说，它将进入轨道（假设它没有受到空气阻力或障碍物的影响）。[44]

简谐运动

图 6：无阻尼弹簧-质量系统会进行简谐运动。

　　考虑一个质量为 $ m $ 的物体，它可以沿着 $ x $ 轴移动，假设在位置 $ x = 0 $ 存在一个平衡点。也就是说，当 $ x = 0 $ 时，作用在物体上的合力为零向量，根据牛顿第二定律，物体将不会加速。如果作用在物体上的力与物体偏离平衡点的位移成正比，且指向平衡点，那么该物体将进行简谐运动。将力写为 $ F = -kx $，牛顿第二定律变为： \[ m \frac{d^2 x}{dt^2} = -kx~ \] 这个微分方程的解为： \[ x(t) = A \cos\left(\omega t\right) + B \sin\left(\omega t\right) ~ \] 其中，频率 $ \omega $ 等于 $ \sqrt{k/m} $，常数 $ A $ 和 $ B $ 可以通过已知的初始条件（例如物体在某个时刻的位移和速度）计算出来，比如 $ t = 0$。

　　简谐振子之所以是概念上重要的例子之一，原因在于它是许多系统在稳定机械平衡附近的良好近似。[注 10] 例如，钟摆在垂直位置有一个稳定的平衡点：如果它静止不动，就会保持在该位置；如果轻微推动，它将来回摆动。在忽略空气阻力和支点摩擦的情况下，作用在钟摆上的力是重力，牛顿第二定律变为 \[ \frac{d^2 \theta}{dt^2} = -\frac{g}{L} \sin \theta~ \] 其中 $ L $ 是钟摆的长度，$ \theta $ 是钟摆偏离垂直方向的角度。当角度 $ \theta $ 很小时，$ \sin \theta $ 近似等于 $ \theta $（参见泰勒级数），因此该表达式简化为简谐振子的方程，频率为 $\omega = \sqrt{g/L}$。

　　简谐振子可能受到阻尼，通常由摩擦或粘性阻力引起，在这种情况下，能量从振子中耗散，振动的振幅会随着时间逐渐减小。简谐振子也可以受到外力驱动，这可能导致共振现象的发生[46]

质量可变的物体

图 7：火箭（如亚特兰蒂斯号航天飞机）通过将物质向一个方向喷射来推动飞船朝另一个方向运动。这意味着被推动的质量——火箭及其剩余的燃料供应——是在不断变化的。

　　牛顿物理学认为物质既不会被创造也不会被消灭，尽管它可能被重新排列。在某些情况下，物体可能因为物质被添加或移除而增加或减少质量。在这种情况下，可以将牛顿定律应用于物质的各个部分，并随时间跟踪哪些部分属于所研究的物体。例如，如果一个质量为 $ M(t) $ 的火箭以速度 $ \mathbf{v}(t) $ 运动，并以相对于火箭的速度 $ \mathbf{u} $ 喷射物质，那么 \[ \mathbf{F} = M\frac{d\mathbf{v}}{dt} - \mathbf{u} \frac{dM}{dt}~ \] 其中 $ \mathbf{F} $ 是净外力（例如行星的引力作用）。[23]:139

3. 功和能

　　物理学家在牛顿时代之后发展了能量的概念，但它已经成为 “牛顿力学” 不可分割的一部分。能量可以大致分为两类：动能（由于物体的运动）和势能（由于物体相对于其他物体的位置）。热能是由热流携带的能量，是一种与物体的宏观运动无关的动能，而是与构成物体的原子和分子的运动有关。根据功-能定理，当一个力作用于物体并且该物体沿着力的方向运动时，力对物体做功，做功的量等于物体动能的变化。[注 11] 在许多感兴趣的情况下，当物体沿封闭回路运动——从一点出发，沿某一轨迹移动并返回起点时，力所做的净功为零。如果是这种情况，那么该力可以表示为一个标量势函数的梯度。[42]:303 \[ \mathbf{F} = -\mathbf{\nabla} U~ \] 这个公式适用于许多力，包括重力，但不适用于摩擦力。实际上，几乎任何没有涉及摩擦力的力学问题都可以用这种方式表达。[45]:19

　　力可以这样表达是由于能量守恒定律的缘故。在没有摩擦力将物体的能量散失为热量的情况下，物体的能量在势能和（非热）动能之间转换，而总能量保持不变。当物体在合力的作用下加速并获得动能时，势能必然减少。因此，作用在物体上的合力取决于势能减少的方式。

4. 刚体运动与旋转

　　刚体是一个尺寸大到不能忽略并且能够在时间中保持形状不变的物体。在牛顿力学中，刚体的运动通常通过将其分为物体质心的运动和围绕质心的运动来理解。

质心

　　叉子、软木塞和牙签物体平衡在牙签部分上方的笔尖整个叉子、软木塞和牙签的质心位于笔尖上方。

　　通过想象物体的质量集中在一个称为质心的单点上，可以理解一个扩展物体运动的关键方面。物体的质心位置取决于物体材料的分布。对于一组具有质量 $ m_1, \ldots, m_N $ 的点状物体，位置为 $ \mathbf{r}_1, \ldots, \mathbf{r}_N $，质心的位置为 \[ \mathbf{R} = \sum_{i=1}^{N} \frac{m_i \mathbf{r}_i}{M}~ \] 其中 $ M $ 是这些物体的总质量。在没有外部合力的情况下，质心将以恒定速度沿直线运动。这适用于例如两个物体的碰撞。如果外部总力不为零，那么质心的速度会像一个质量为 $ M $ 的点物体一样发生变化。这是因为在物体集合内部的力，即物体之间相互作用的力，根据牛顿第三定律成平衡对存在。在一个由两个物体组成的系统中，如果其中一个物体的质量远大于另一个物体的质量，那么质心将近似与质量较大的物体的位置重合。[18]:22–24

图 8：叉子、软木塞和牙签的总质心位于笔尖上方。

牛顿定律的旋转类比

　　当牛顿定律应用于旋转的扩展物体时，会引入一些与原定律中的量相对应的新量。质量的类比是转动惯量，动量的对应量是角动量，而力的对应量是力矩。

　　角动量是相对于某个参考点计算的。[50] 如果从参考点到物体的位移向量为 $ \mathbf{r} $，且物体的动量为 $ \mathbf{p} $，那么物体相对于该点的角动量可以通过向量叉积表示为： \[ \mathbf{L} = \mathbf{r} \times \mathbf{p}~ \] 对角动量取时间导数得到： \[ \frac{d\mathbf{L}}{dt} = \left( \frac{d\mathbf{r}}{dt} \right) \times \mathbf{p} + \mathbf{r} \times \frac{d\mathbf{p}}{dt} = \mathbf{v} \times m\mathbf{v} + \mathbf{r} \times \mathbf{F}~ \] 第一项消失，因为 $ \mathbf{v} $ 和 $ m\mathbf{v} $ 方向相同。剩下的项是力矩： \[ \mathbf{\tau} = \mathbf{r} \times \mathbf{F}~ \] 当力矩为零时，角动量保持不变，就像当力为零时，动量保持不变。[18]:14–15 如果物体位于参考点（即 $ \mathbf{r} = 0 $）或者力 $ \mathbf{F} $ 和位移向量 $ \mathbf{r} $ 沿同一方向，力矩可以为零，即使力不为零。

　　点质量集合的角动量（因此也包括扩展物体的角动量）可以通过将每个点的贡献相加来得到。这为描述物体绕轴旋转提供了一种方法，即通过将各个部分的角动量相加。结果取决于所选的旋转轴、物体的形状和转速。[18]:28

多体引力系统

图 9：三个相互吸引的点或物体的动画

　　牛顿的万有引力定律指出，任何物体都会沿连接它们的直线吸引其他物体。吸引力的大小与它们质量的乘积成正比，与它们之间距离的平方成反比。寻找逆平方力法则产生的轨道形状被称为开普勒问题。开普勒问题可以通过多种方式解决，包括证明拉普拉斯–龙格–伦兹向量是恒定的，[51] 或通过对二维简谐振子应用对偶变换。[52] 不论使用何种解法，结果表明轨道是圆锥曲线，即椭圆（包括圆）、抛物线或双曲线。轨道的离心率，以及圆锥曲线的类型，由轨道物体的能量和角动量决定。行星没有足够的能量逃离太阳，因此它们的轨道近似为椭圆；由于行星相互之间存在引力作用，实际轨道并不完全是圆锥曲线。

　　如果增加一个第三个质量，开普勒问题就变成了三体问题，一般来说，三体问题没有封闭形式的精确解。也就是说，无法从牛顿定律所隐含的微分方程出发，经过有限序列的标准数学运算后得到描述三体运动随时间变化的方程。[53][54] 数值方法可以应用于三体问题，得到有用但近似的结果。[55] 物体的位置和速度可以存储在计算机的内存变量中；利用牛顿定律来计算在短时间间隔内速度的变化，已知速度后，可以计算该时间间隔内的位置变化。这个过程会循环执行，以近似计算物体的轨迹。一般来说，时间间隔越短，近似结果越准确。[56]

5. 混沌与不可预测性

非线性动力学

图 10：三个双摆，几乎在完全相同的初始条件下开始运动，随着时间的推移，它们的运动逐渐分离。

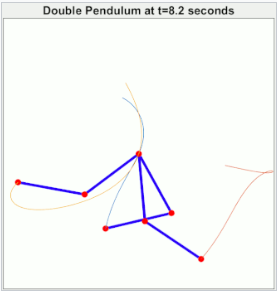
　　牛顿运动定律允许出现混沌现象。[57][58] 换句话说，遵守牛顿定律的物理系统可能对初始条件表现出敏感依赖性：系统中某一部分的位置或速度的微小变化可以在短时间内导致整个系统表现出截然不同的行为。著名的例子包括三体问题、双摆、动力学台球和费米–帕斯塔–乌拉姆–清谷问题。

　　牛顿定律可以应用于流体，通过将流体视为由无数微小部分组成，每个部分对其邻近部分施加力。欧拉动量方程是牛顿第二定律在流体动力学中的表达形式。[59][60] 流体由速度场描述，即一个函数 $ \mathbf{v}(\mathbf{x}, t) $，它为空间和时间中的每一点分配一个速度向量。随着流体流动而移动的小物体的速度可以由于两种原因发生变化：第一，因为其位置的速度场随时间变化；第二，因为它移动到了一个速度场具有不同值的新位置。因此，当牛顿第二定律应用于流体的微小部分时，物体的加速度 $ \mathbf{a} $ 包含两个项，称为总导数或物质导数。微小部分的质量取决于流体密度，并且如果流体压力在物体的不同侧面不均匀，物体将受到净力。因此，方程 $ \mathbf{a} = \mathbf{F}/m $ 变为： \[ \frac{\partial \mathbf{v}}{\partial t} + (\mathbf{\nabla} \cdot \mathbf{v})\mathbf{v} = -\frac{1}{\rho} \mathbf{\nabla} P + \mathbf{f}~ \] 其中 $ \rho $ 是密度，$ P $ 是压力，$ \mathbf{f} $ 代表外部影响，例如重力。如果将粘度的影响考虑进去，欧拉方程将转化为纳维尔-斯托克斯方程： \[ \frac{\partial \mathbf{v}}{\partial t} + (\mathbf{\nabla} \cdot \mathbf{v})\mathbf{v} = -\frac{1}{\rho} \mathbf{\nabla} P + \nu \nabla^2 \mathbf{v} + \mathbf{f}~ \] 其中 $ \nu $ 是动力粘度系数。[59]

奇点

　　根据数学推导，一组遵循牛顿定律运动的点质量物体有可能以极大的力量将其中一些物体推出，使它们在有限时间内飞向无穷远。[61] 这种不符合物理规律的行为被称为 “非碰撞奇点”，[54] 它依赖于这些物体是点状并且能够无限接近彼此，同时也依赖于牛顿物理中不存在相对论速度限制。[62]

　　目前尚不清楚欧拉方程和纳维尔-斯托克斯方程是否会表现出类似的现象，即初始光滑解在有限时间内 “爆发”。关于纳维尔-斯托克斯方程解的存在性和光滑性的问题是千禧年大奖问题之一。[63]

6. 与经典物理其他表述的关系

　　经典力学可以通过多种不同的方式进行数学表述，除了 “牛顿式” 描述（当然，牛顿式描述本身也包含了牛顿之前和之后其他人的贡献）。这些不同表述的物理内容与牛顿式相同，但它们提供了不同的见解，并有助于不同类型的计算。例如，拉格朗日力学有助于揭示对称性与守恒定律之间的联系，并且在计算受限物体的运动时非常有用，比如限制沿曲线路径或球面运动的物体。[18]:48 哈密顿力学在统计物理中很方便，[64][65]:57 进一步揭示了对称性的见解，[18]:251 并且可以发展成用于微扰理论的复杂技术。[18]:284 由于这些主题的广泛性，这里将简要讨论它们如何重新表述牛顿运动定律。

拉格朗日力学

　　拉格朗日力学与牛顿的表述不同，它考虑的是整个轨迹，而不是预测物体在单个瞬间的运动。[18]:109 在拉格朗日力学中，传统上用 $ q $ 表示位置，用 $ \dot{q} $ 表示速度。最简单的例子是一个具有质量的点粒子，其拉格朗日量可以写为动能和势能之差： \[ L(q, \dot{q}) = T - V~ \] 其中，动能为 \[ T = \frac{1}{2} m \dot{q}^2~ \] 势能是位置的某个函数 $ V(q) $。粒子在初始位置 $ q_i $ 和最终位置 $ q_f $ 之间的物理路径，是使拉格朗日量积分保持 “驻值” 的路径。也就是说，物理路径的性质是，当它受到微小扰动时，拉格朗日量的积分在一阶近似下不会发生变化。变分法为找到这条路径提供了数学工具。[42]:485 通过应用变分法，可以得到粒子的欧拉-拉格朗日方程： \[ \frac{d}{dt}\left(\frac{\partial L}{\partial \dot{q}}\right) = \frac{\partial L}{\partial q}~ \] 对拉格朗日量求偏导数后得到： \[ \frac{d}{dt}(m\dot{q}) = -\frac{dV}{dq}~ \] 这实际上是牛顿第二定律的另一种表达形式。左边是动量的时间导数，右边是用势能表示的力。[9]:737

　　朗道和利夫希兹认为，与从牛顿定律入手相比，拉格朗日的表述使经典力学的概念内容更加清晰。[26] 拉格朗日力学提供了一个方便的框架来证明诺特定理，该定理将对称性与守恒定律联系起来。[66] 动量守恒可以通过将诺特定理应用于多粒子系统的拉格朗日量推导出来，因此牛顿第三定律可以被视为一个定理，而非假设。[18]:124

哈密顿量

图 11：艾米·诺特（Emmy Noether）在 1915 年证明了一个著名的定理，该定理将对称性与守恒定律联系起来，是现代物理学中的重要发展，并且可以通过拉格朗日或哈密顿力学的语言方便地表达。

　　在哈密顿力学中，系统的动力学由一个称为哈密顿量的函数表示，在许多感兴趣的情况下，这个函数等于系统的总能量。[9]:742 哈密顿量是所有构成系统的物体的位置和动量的函数，并且它也可能显式依赖于时间。位置和动量变量的时间导数由哈密顿方程中的哈密顿量的偏导数给出。[18]:203 最简单的例子是一个受到势影响的点质量 $ m $ 被限制在直线上运动。用 $ q $ 表示位置坐标，$ p $ 表示物体的动量，哈密顿量为 \[ {\mathcal {H}}(p,q) = \frac{p^2}{2m} + V(q)~ \] 在这个例子中，哈密顿方程为： \[ \frac{dq}{dt} = \frac{\partial {\mathcal {H}}}{\partial p}~ \] 以及 \[ \frac{dp}{dt} = -\frac{\partial {\mathcal {H}}}{\partial q}~ \] 对这些偏导数进行计算，前一个方程变为： \[ \frac{dq}{dt} = \frac{p}{m}~ \] 这重现了熟知的动量等于物体质量与速度乘积的表述。动量的时间导数为： \[ \frac{dp}{dt} = -\frac{dV}{dq}~ \] 将势能的负导数识别为力后，这实际上又是牛顿第二定律的表述。[57][9]:742

　　如同在拉格朗日表述中一样，在哈密顿力学中，动量守恒可以通过诺特定理推导得出，这使得牛顿第三定律成为推导出的结果，而不是假设。[18]:251

　　在关于改革标准入门物理课程的提议中，有一种建议是先教授能量概念，再教授力的概念，本质上就是 “入门哈密顿力学”。[67][68]

哈密顿-雅可比方程

　　哈密顿-雅可比方程为经典力学提供了另一种表述，使其在数学上类似于波动光学。[18]:284[69] 这种表述也使用哈密顿量函数，但方式不同于上述表述。物体或物体系统所走的路径是由一个位置 $ \mathbf{q}_1, \mathbf{q}_2, \ldots, t $ 和时间 $ t $ 的函数 $ S(\mathbf{q}_1, \mathbf{q}_2, \ldots, t) $ 推导出来的。哈密顿量被纳入哈密顿-雅可比方程，该方程是关于 $ S $ 的一个微分方程。物体随时间的运动使其轨迹垂直于常数 $ S $ 的曲面，类似于光线垂直于波前传播。这在单个点质量的情况下最简单，其中 $ S $ 是一个 $ S(\mathbf{q}, t) $ 的函数，点质量沿着 $ S $ 变化最剧烈的方向运动。换句话说，点质量的动量是 $ S $ 的梯度： \[ \mathbf{v} = \frac{1}{m} \nabla S~ \] 点质量的哈密顿-雅可比方程为： \[ -\frac{\partial S}{\partial t} = H\left(\mathbf{q}, \nabla S, t\right)~ \] 通过考虑一个在时间不变的势能 $ V(\mathbf{q}) $ 下运动的点质量，可以看出它与牛顿定律的关系，此时哈密顿-雅可比方程变为： \[ -\frac{\partial S}{\partial t} = \frac{1}{2m} \left(\nabla S\right)^2 + V(\mathbf{q})~ \] 对方程两边取梯度，得到： \[ -\nabla \frac{\partial S}{\partial t} = \frac{1}{2m} \nabla \left(\nabla S\right)^2 + \nabla V~ \] 对左侧的偏导数顺序进行互换，并对右侧第一项应用乘方法则和链式法则： \[ -\frac{\partial}{\partial t} \nabla S = \frac{1}{m} \left(\nabla S \cdot \nabla \right) \nabla S + \nabla V~ \] 将与 $ S $ 梯度相关的项收集在一起： \[ \left[\frac{\partial}{\partial t} + \frac{1}{m} \left(\nabla S \cdot \nabla \right)\right] \nabla S = - \nabla V~ \] 这是牛顿第二定律的另一种表达形式。[70] 方括号中的表达式是总导数或物质导数，[71] 其中第一项表示函数在固定位置随时间的变化，第二项捕捉到移动的粒子在其旅行过程中所看到的不同函数值： \[ \left[\frac{\partial}{\partial t} + \frac{1}{m} \left(\nabla S \cdot \nabla \right)\right] = \left[\frac{\partial}{\partial t} + \mathbf{v} \cdot \nabla \right] = \frac{d}{dt}~ \]

7. 与其他物理理论的关系

热力学与统计物理

图 12：一项模拟展示了一个较大但仍然是微观的粒子（黄色）被一群较小的粒子包围，演示布朗运动。

　　在统计物理中，气体的动理论将牛顿运动定律应用于大量（通常是阿伏伽德罗常数量级）的粒子。动理论可以解释例如气体对容器施加的压力，它是许多原子撞击容器并传递微小动量的总和。[65]:62

　　朗之万方程是牛顿第二定律的一个特殊情况，用于描述一个被更小粒子随机轰击的小物体的运动。[72]:235 它可以写为 \[ m\mathbf {a} = -\gamma \mathbf {v} + \mathbf {\xi }~ \] 其中，$ \gamma $ 是阻力系数，$ \mathbf {\xi } $ 是一个随时间随机变化的力，代表与周围粒子碰撞的净效应。这个方程用于模拟布朗运动。[73]

电磁学

　　牛顿的三大定律可以应用于涉及电和磁现象的现象中，尽管存在一些微妙之处和注意事项。

　　库仑定律描述了两静止带电体之间的电力，其数学形式与牛顿的万有引力定律非常相似：力与电荷的乘积成正比，与它们之间距离的平方成反比，方向沿着它们之间的直线。电荷 $ q_1 $ 对电荷 $ q_2 $ 施加的库仑力的大小等于电荷 $ q_2 $ 对电荷 $ q_1 $ 施加的力，且它们的方向正好相反。因此，库仑定律与牛顿第三定律是一致的。[74]

　　电磁学将力视为由场作用于电荷产生的。洛伦兹力定律为作用在带电体上的力提供了表达式，该力可以代入牛顿第二定律以计算加速度。[75]:85 根据洛伦兹力定律，带电体在电场中会受到沿电场方向的力，该力与其电荷 $ q $ 和电场强度成正比。此外，运动的带电体在磁场中也会受到一个力，该力与其电荷成正比，方向垂直于磁场和物体的运动方向。使用向量叉积表示： \[ \mathbf{F} = q\mathbf{E} + q\mathbf{v} \times \mathbf{B}~ \] 如果电场消失（$ \mathbf{E} = 0 $），那么力将垂直于电荷的运动方向，类似于上面研究的匀速圆周运动的情况，此时电荷会绕着磁场线旋转（或更一般地，沿螺旋轨迹运动），其回旋频率为 $ \omega = qB/m $。[72]:222 质谱仪通过对运动中的电荷施加电场和/或磁场，并测量由此产生的加速度，依据洛伦兹力定律得出质量与电荷的比值。[76]

　　带电物体的集合并不总是遵循牛顿第三定律：一个物体的动量可以发生变化，而另一个物体的动量却没有相应的变化。这种差异是由电磁场本身携带的动量来解释的。电磁场的单位体积动量与坡印廷矢量成正比。[77]:184[78]

图 13：洛伦兹力定律的作用：电子在磁场作用下被弯曲成圆形轨迹。

　　电磁学与牛顿第一定律之间存在一些微妙的概念冲突：麦克斯韦的电磁理论预测，电磁波在真空中以恒定的、确定的速度传播。因此，某些惯性观察者似乎比其他观察者具有特权地位，即那些测量到光速并发现其符合麦克斯韦方程预测值的观察者。换句话说，光为速度提供了一个绝对标准，而惯性原理则认为不应存在这样的标准。这个矛盾在狭义相对论中得到了解决，该理论修正了空间和时间的概念，使得所有惯性观察者都会在真空中测量到相同的光速。[注 12]

狭义相对论

　　在狭义相对论中，威尔切克称为 “牛顿第零定律” 的规则失效：复合物体的质量不仅仅是其各个部分质量的总和。[81]:33 牛顿第一定律，即惯性运动，仍然成立。牛顿第二定律的某种形式，即力是动量变化率，也依然有效，动量守恒同样成立。然而，动量的定义发生了改变。其结果之一是，物体运动得越快，越难以加速，因此无论施加多大的力，物体都无法被加速到光速。根据具体问题，狭义相对论中的动量可以表示为三维向量：$\mathbf{p} = m\gamma \mathbf{v}$ 其中 $ m $ 是物体的静止质量，$ \gamma $ 是洛伦兹因子，取决于物体的速度。另一种方式是用四维向量表示动量和力。[82]:107

　　在狭义相对论中，牛顿第三定律必须被修改。第三定律涉及两个物体在同一时刻的相互作用力，而狭义相对论的一个关键特点是同时性是相对的。相对于一个观察者同时发生的事件，可能在另一个观察者看来是不同时间发生的。因此，在某个观察者的参考系中，作用力和反作用力可能不完全相反，交互物体的总动量可能不守恒。通过将描述物体相互作用的场中存储的动量纳入考虑，动量守恒得以恢复。[83][84]

　　当涉及的速度相对于光速较小时，牛顿力学是狭义相对论的良好近似。[85]:131

广义相对论

　　广义相对论是一种超越牛顿引力理论的引力理论。在广义相对论中，牛顿力学中的引力被重新诠释为时空的弯曲。在牛顿力学中归因于引力作用的轨道等弯曲路径，并不是由于力将物体从理想的直线路径上偏转，而是物体试图在一个由于其他质量的存在而弯曲的背景中自由下落。物理学家约翰·阿奇博尔德·惠勒的一句名言很好地总结了这一理论：“时空告诉物质如何运动；物质告诉时空如何弯曲。”[86][87] 惠勒本人将这种相互关系看作是牛顿第三定律的现代、广义形式。[86] 物质分布与时空曲率之间的关系由爱因斯坦场方程给出，需用张量运算来表达。[81]:43[88]

　　当引力效应较弱，物体的运动速度相对于光速较慢时，牛顿引力理论是广义相对论预测的良好近似。[79]:327[89]

量子力学

　　量子力学是一种物理学理论，最初发展是为了理解微观现象，即分子、原子或亚原子粒子尺度的行为。一般而言，系统越小，适当的数学模型越需要理解量子效应。量子物理学的概念基础与经典物理学非常不同。与其认为位置、动量和能量等量是物体的固有属性，不如说是考虑在进行某种类型的测量时可能出现的结果。量子力学允许物理学家计算特定测量可能引出某一特定结果的概率。[90][91] 测量的期望值是可能结果的平均值，按其发生概率加权。[92]

　　爱伦费斯特定理提供了量子期望值与牛顿第二定律之间的联系，但这种联系并不精确，因为量子物理与经典物理在根本上不同。在量子物理中，位置和动量由称为厄米算子的数学实体表示，波恩规则用于计算位置测量或动量测量的期望值。这些期望值通常会随时间变化；也就是说，取决于进行测量的时间（例如位置测量），不同结果的概率会有所变化。爱伦费斯特定理大致表明，描述这些期望值如何随时间变化的方程形式类似于牛顿第二定律。然而，量子效应越明显，在某种情况下，从这种相似性中得出有意义的结论就越困难。[注 13]

8. 历史

图 14：以赛亚·牛顿（1643–1727），在 1689 年由戈弗雷·奈勒创作的肖像画中。

图 15：牛顿本人《自然哲学的数学原理》的一本副本，带有为第二版手写的修订，现存于剑桥大学三一学院的雷恩图书馆。

图 16：牛顿的第一定律和第二定律，拉丁文版，摘自 1687 年原版的《数学原理》。

　　牛顿运动定律中涉及的概念——质量、速度、动量、力——在早期的研究中已有先驱，牛顿力学的内容在牛顿之后得到了进一步的发展。牛顿将天体运动的知识与地球上的现象研究相结合，证明了一种力学理论可以同时解释这两者。[注 14]

古代与中世纪背景

亚里士多德与 “强制” 运动

图 17：亚里士多德 (公元前 384–322 年)

　　物理学这一学科通常可以追溯到亚里士多德，但相关概念的历史因多种因素而变得模糊不清。要在亚里士多德的概念与现代概念之间建立精确的对应关系并不简单：亚里士多德没有明确区分我们所称的速度和力，使用同一个术语来指代密度和粘度，并将运动理解为总是在介质中进行的，而不是在空间中。此外，一些常被称为 “亚里士多德式” 的概念可能更恰当地归属于他的追随者及其评论者。[97] 这些评论者发现，亚里士多德的物理学难以解释抛射体的运动。[注 15] 亚里士多德将运动分为两类：“自然运动” 和 “强制运动”。地球上的固体物质的 “自然” 运动是下落，而 “强制” 运动则可以推动物体向侧面运动。而且，在亚里士多德的物理学中，“强制” 运动需要一个直接的原因；一旦与其 “强制” 运动的原因分离，物体将恢复其 “自然” 行为。然而，标枪在离开投掷者的手后仍然继续运动。亚里士多德因此得出结论，标枪周围的空气必须被赋予推动标枪向前运动的能力。

菲洛波努斯与动力说

　　约翰·菲洛波努斯是一位活跃于六世纪的拜占庭希腊思想家，他认为亚里士多德的想法荒谬：同一种介质——空气，既要维持运动，又要阻碍运动。如果亚里士多德的观点是正确的，菲洛波努斯讽刺道，那么军队应该可以通过风箱吹气来发射武器。菲洛波努斯主张，当一个物体被设置为运动时，它会被赋予一种品质，即 “动力”，这种动力存在于物体本身之内。只要这种动力持续存在，物体就会继续运动。[99]:47 在接下来的几个世纪里，动力理论的不同版本由努尔·丁·比特鲁吉、阿维森纳、阿布·巴拉卡特·巴格达迪、让·布里丹和萨克森的阿尔伯特等人提出。回顾来看，动力的概念可以被视为现代动量概念的前身。[注 16] 对于物体根据某种动力运动的直觉在许多初级物理学学生中依然存在。[101]

惯性与第一定律

图 18：勒内·笛卡尔 (1596–1650)

　　法国哲学家勒内·笛卡尔在 1629 年至 1633 年间写作的《世界》（*Traité du monde et de la lumière*）中，通过他的 “自然法则” 引入了惯性这一概念。然而，《世界》支持日心说的宇宙观，而这一观点在 1633 年引发了伽利略·伽利莱与罗马天主教宗教裁判所之间的重大冲突。笛卡尔知晓这一争议，并不愿卷入其中。因此，《世界》直到他去世十年后的 1664 年才得以出版。[102]

　　现代惯性概念归功于伽利略。基于他的实验，伽利略得出结论，运动物体的 “自然” 行为是继续运动，直到有其他事物干扰它。在 1638 年的《两门新科学》中，伽利略写道：[103][104]

　　 “设想任何一个粒子沿着无摩擦的水平平面被抛射出去；那么，根据之前更详细的解释，我们知道，这个粒子将在同一平面上以均匀且永恒的运动前进，只要这个平面没有边界。”

图 19：伽利略·伽利莱 (1564–1642)

　　伽利略认识到，在抛体运动中，地球的重力只影响垂直运动，而不影响水平运动。[105] 然而，伽利略的惯性概念并不完全是后来被确立为牛顿第一定律的那种。伽利略认为，物体在长距离的惯性运动中会沿着地球的曲线运动。这个观点后来被艾萨克·贝克曼、笛卡尔和皮埃尔·伽森迪纠正，他们认识到惯性运动应该是沿直线进行的。[106] 笛卡尔在 1644 年出版的《哲学原理》（*Principia Philosophiae*）中发布了他的自然法则（运动定律），并且将其中的日心说部分淡化了。[107][102]

　　 自然第一定律：每一事物若不受干扰，将保持其原有状态；因此，任何运动的物体会持续运动，直到某种事物阻止它。

　　 自然第二定律：每一个运动的物体若不受干扰，将沿直线运动；因此，任何沿圆周运动的物体总是倾向于远离圆心。

图 20：做圆周运动的球被剪断了绳子，沿切线飞出。

　　根据美国哲学家理查德·J·布莱克威尔的说法，荷兰科学家克里斯蒂安·惠更斯在 1656 年就推导出了他自己简洁的版本的定律。[108] 直到他去世八年后的 1703 年，这一定律才在《碰撞运动论》的开篇段落中发表。

　　 假设一：任何已经处于运动状态的物体将以相同的速度沿直线永远运动，除非受到阻碍。

　　据惠更斯说，这一定律早已为伽利略、笛卡尔等人所知。[108]

力与第二定律

图 21：克里斯蒂安·惠更斯 (1629–1695)

　　克里斯蒂安·惠更斯在他的《摆钟》（1673 年）中提出了这样一个假设：“无论重力的来源是什么，它的作用使物体的运动由两个部分组成：一个是某个方向上的匀速运动，另一个是由重力引起的向下运动。” 牛顿的第二定律将这一假设从重力推广到所有的力。[109]

　　牛顿物理学的一个重要特点是，力可以在没有物理接触的情况下远距离作用。[注 17] 例如，尽管太阳和地球相距数百万公里，它们仍通过引力相互拉动。这与笛卡尔等人提出的观点形成对比，他们认为太阳通过在透明的以太物质漩涡中旋转行星来使其保持在轨道上。[116] 牛顿曾考虑过以太解释力的说法，但最终放弃了。[114] 威廉·吉尔伯特及其他人对磁力的研究为思考无形力创造了先例，[114] 由于无法通过以太模型找到一个对其引力定律的定量解释，牛顿最终宣布，“我不虚构假设”：无论是否能找到像笛卡尔漩涡那样的模型来支撑《自然哲学的数学原理》中的运动和引力理论，判断它们的首要依据必须是它们成功的预测。[117] 而事实上，自牛顿以来，所有试图构建这种模型的尝试都失败了。

动量守恒与第三定律

图 22：约翰内斯·开普勒 (1571–1630)

　　约翰内斯·开普勒提出，引力作用是相互的——例如，月球拉动地球，地球也拉动月球——但他并未主张这对力是大小相等且方向相反的。[118] 在他的《哲学原理》（1644 年）中，笛卡尔引入了这样一个概念：在物体碰撞过程中，“运动量” 保持不变。笛卡尔定义这一数量时并不精确，他将每个物体的速度与 “大小” 的乘积相加，其中 “大小” 对他来说既包含体积，也包含表面积。[119] 此外，笛卡尔认为宇宙是充满物质的，即一个充盈体，因此任何运动都需要物体在移动时置换介质。

　　在 1650 年代，惠更斯研究了硬球碰撞，并推导出了如今被称为动量守恒的原理。[120][121] 克里斯托弗·雷恩后来推导出了与惠更斯相同的弹性碰撞规则，约翰·沃利斯则将动量守恒应用于研究非弹性碰撞。牛顿引用了惠更斯、雷恩和沃利斯的研究来支持他第三定律的有效性。[122]

　　牛顿逐步得出了他的一系列三大定律。在 1684 年写给惠更斯的一份手稿中，他列出了四条定律：惯性原理、力改变运动的原理、一条关于相对运动的陈述（今天称为伽利略不变性），以及物体之间的相互作用不会改变它们质心运动的规则。在后来的手稿中，牛顿增加了作用与反作用定律，同时指出这一定律与关于质心的定律互为推论。牛顿可能在 1685 年确定了《自然哲学的数学原理》中的表述，即将三条主要定律作为基础，并将其他陈述简化为推论。[123]

《自然哲学的数学原理》之后

　　牛顿通过描述物体所受的力与其运动变化（即动量）成正比来表达他的第二定律。当他撰写《自然哲学的数学原理》时，他已经发展了微积分（他称之为 “流数法”），但在《原理》中并没有明确使用它，可能是因为他认为欧几里得几何传统的推理更加严谨。[125]:15[126] 因此，《原理》并没有将加速度表示为位置的二阶导数，也没有给出第二定律的形式 $ F = ma $。这种形式的第二定律至少在 1716 年由雅各布·赫尔曼（Jakob Hermann）为恒定力的特殊情况写出；莱昂哈德·欧拉（Leonhard Euler）在 1740 年代将其作为基本前提使用。[127] 欧拉开创了对刚体运动的研究[128]，并奠定了流体动力学的基本理论。[129] 皮埃尔-西蒙·拉普拉斯的五卷本《天体力学论》（1798–1825）摒弃了几何方法，完全通过代数表达式发展了力学，并解决了《原理》未解决的问题，如完整的潮汐理论。[130]

　　能量的概念在后牛顿时期成为牛顿力学中的一个关键部分。惠更斯对硬球碰撞的解表明，在这种情况下，不仅动量守恒，动能也守恒（或者，更确切地说，是我们可以回溯性地识别为总动能的一半的量守恒）。关于在所有其他过程中（如非弹性碰撞和由摩擦减速的运动）守恒的是什么，直到 19 世纪才得到解决。关于这一问题的讨论与牛顿和莱布尼茨的形而上学观点的哲学争论有所交叠，"力"一词的变体有时用于表示我们今天所称的各种能量。例如，在 1742 年，艾米莉·迪·夏特莱写道：“死力是指简单的运动趋势：例如一个即将松弛的弹簧；活力是指物体实际运动时所具有的能量。” 用现代术语来说，"死力"和"活力"分别对应于势能和动能。[131] 能量守恒直到理解机械功的能量可以耗散为热能后，才被确立为一个普遍原理。[132][133] 在能量概念得到了坚实的基础后，牛顿定律便可以通过首先考虑能量的经典力学表述中推导出来，如上文所述的拉格朗日和哈密顿表述。

　　现代对牛顿定律的讲解使用了向量数学，而这一领域直到 19 世纪末和 20 世纪初才得以发展。由乔赛亚·威拉德·吉布斯和奥利弗·赫维赛德开创的向量代数源于并在很大程度上取代了由威廉·罗恩·汉密尔顿发明的四元数系统。[134][135]

图 23：《天体机制》（1831 年）第 157 页，玛丽·萨默维尔扩展版的拉普拉斯《天体力学论》前两卷。[124] 在此，萨默维尔从开普勒的行星运动定律推导出反平方引力定律。

另见

欧拉运动定律
经典力学史
以人名命名的定律列表
经典力学中的方程列表
以人名命名的科学定律列表
经典力学和量子力学教材列表
诺顿穹顶

9. 注释

例如，参见 Zain。[4]:1-2 大卫·通（David Tong）指出：“粒子被定义为一个尺寸可以忽略不计的物体：例如，电子、网球或行星。显然，这一说法的有效性取决于具体的语境……”[5]
牛顿，I. (1999)。《自然哲学的数学原理》。由 Cohen, I.B. 和 Whitman, A. 翻译。洛杉矶：加利福尼亚大学出版社。
牛顿，艾萨克；Chittenden, N. W.；Motte, Andrew；Hill, Theodore Preston (1846)。牛顿的《自然哲学的数学原理》。加利福尼亚大学图书馆。Daniel Adee。
Zain, Samya (2019)。经典力学技术：从拉格朗日力学到牛顿力学。物理学研究所。ISBN 978-0-750-32076-4。OCLC 1084752471。
Tong, David (2015 年 1 月)。《经典动力学：剑桥大学第二部分数学课程》 (PDF)。剑桥大学。2022 年 2 月 12 日获取。
Hughes-Hallett, Deborah；McCallum, William G.；Gleason, Andrew M.；等 (2013)。《微积分：单变量与多变量》（第 6 版）。霍博肯，新泽西：Wiley。第 76-78 页。ISBN 978-0-470-88861-2。OCLC 794034942。
Thompson, Silvanus P.；Gardner, Martin (1998)。《轻松学微积分》。麦克米伦。第 84-85 页。ISBN 978-0-312-18548-0。OCLC 799163595。
McDermott, Lillian C.; Rosenquist, Mark L.; van Zee, Emily H. (1987 年 6 月)。“学生在将图表与物理学相联系时遇到的困难：来自运动学的例子”。美国物理学杂志，55 (6): 503–513。Bibcode:1987AmJPh..55..503M。doi:10.1119/1.15104。ISSN 0002-9505。
Gbur, Greg (2011)。《光学物理与工程的数学方法》。英国剑桥：剑桥大学出版社。ISBN 978-0-511-91510-9。OCLC 704518582。
Driver, Rosalind; Warrington, Lynda (1985 年 7 月 1 日)。“学生在问题情境中使用能量守恒原理”。物理教育，20 (4): 171–176。Bibcode:1985PhyEd..20..171D。doi:10.1088/0031-9120/20/4/308。S2CID 250781921。
Brookes, David T.; Etkina, Eugenia (2009 年 6 月 25 日)。“‘力’、本体论与语言”。物理评论特别专题 - 物理教育研究，5 (1): 010110。Bibcode:2009PRPER...5a0110B。doi:10.1103/PhysRevSTPER.5.010110。ISSN 1554-9178。
Urone, Paul Peter; Hinrichs, Roger; Dirks, Kim; Sharma, Manjula (2021)。《大学物理》。OpenStax。ISBN 978-1-947172-01-2。OCLC 895896190。
Eddington, Arthur (1929)。《物理世界的本质》。纽约：麦克米伦。第 123–125 页。
Frautschi, Steven C.; Olenick, Richard P.; Apostol, Tom M.; Goodstein, David L. (2007)。《力学宇宙：力学与热学》（高级版）。剑桥 [剑桥郡]：剑桥大学出版社。ISBN 978-0-521-71590-4。OCLC 227002144。
Hoek, D. (2023)。“仅有强制变化：惯性的新解读”。科学哲学，90 (1): 60–73。arXiv:2112.02339。doi:10.1017/psa.2021.38。
Pappas, Stephanie (2023 年 9 月 5 日)。“牛顿第一定律的翻译错误在近 300 年后被发现”。科学美国人。
Resnick, Robert (1968)。《狭义相对论导论》。Wiley。第 8–16 页。OCLC 1120819093。
José, Jorge V.; Saletan, Eugene J. (1998)。《经典动力学：现代方法》。英国剑桥：剑桥大学出版社。ISBN 978-1-139-64890-5。OCLC 857769535。
Brading, Katherine (2019 年 8 月)。“关于牛顿《原理》中的杆和钟的一点注释”。科学史与哲学研究 B 部分：现代物理学史与哲学研究，67: 160–166。Bibcode:2019SHPMP..67..160B。doi:10.1016/j.shpsb.2017.07.004。S2CID 125131430。
Feather, Norman (1959)。《质量、长度和时间物理学导论》。英国：大学出版社。第 126–128 页。
Resnick, Robert；Halliday, David (1966)。“第 5-4 节：质量；牛顿第二定律”。物理学。John Wiley & Sons。LCCN 66-11527。
Rosengrant, David；Van Heuvelen, Alan；Etkina, Eugenia (2009 年 6 月 1 日)。“学生是否使用并理解受力图？”。物理评论特别专题 - 物理教育研究，5 (1): 010108。Bibcode:2009PRPER...5a0108R。doi:10.1103/PhysRevSTPER.5.010108。ISSN 1554-9178。
Kleppner, Daniel；Kolenkow, Robert J. (2014)。《力学导论》（第 2 版）。剑桥：剑桥大学出版社。ISBN 978-0-521-19811-0。OCLC 854617117。
Eisenbud, Leonard (1958)。“论经典运动定律”。美国物理学杂志，26: 144–159。doi:10.1119/1.1934608。
Feynman, Richard P.; Leighton, Robert B.; Sands, Matthew L. (1989) [1965]。《费曼物理学讲义》，第一卷。马萨诸塞州雷丁：艾迪生-韦斯利出版社。ISBN 0-201-02010-6。OCLC 531535。
Landau, Lev D.; Lifshitz, Evgeny M. (1969)。《力学》。理论物理课程，第 1 卷。由 J. B. Sykes 和 J. S. Bell 翻译（第 2 版）。佩加蒙出版社。p. vii。ISBN 978-0-080-06466-6。OCLC 898931862。确实，只有通过这种方法，才能使阐述形成一个逻辑整体，避免对基本力学量的同义反复定义。此外，这种方法也更为简单，并且提供了最完整、直接的解决力学问题的手段。
Moebs, William; et al. (2023)。“5.5 牛顿第三定律”。大学物理学，第一卷。OpenStax。p. 220。ISBN 978-1-947172-20-3。
Gonick, Larry; Huffman, Art (1991)。《漫画物理学指南》。HarperPerennial。p. 50。ISBN 0-06-273100-9。
Low, David J.; Wilson, Kate F. (2017 年 1 月)。“竞争性知识结构在削弱学习中的作用：牛顿第二和第三定律”。美国物理学杂志，85 (1): 54–65。Bibcode:2017AmJPh..85...54L。doi:10.1119/1.4972041。ISSN 0002-9505。
Stocklmayer, Sue; Rayner, John P.; Gore, Michael M. (2012 年 10 月)。“改变牛顿定律的顺序——为何与如何应将第三定律置于首位”。物理教师，50 (7): 406–409。Bibcode:2012PhTea..50..406S。doi:10.1119/1.4752043。ISSN 0031-921X。
Hellingman, C. (1992 年 3 月)。“重新审视牛顿第三定律”。物理教育，27 (2): 112–115。Bibcode:1992PhyEd..27..112H。doi:10.1088/0031-9120/27/2/011。ISSN 0031-9120。S2CID 250891975。
Hodanbosi, Carol (1996 年 8 月)。Fairman, Jonathan G. (编)。“第三运动定律”。www.grc.nasa.gov。
Wilczek, Frank (2003)。“质量的起源” (PDF)。麻省理工学院物理学年刊 2003。2022 年 1 月 13 日获取。
Scherr, Rachel E.; Redish, Edward F. (2005 年 1 月 1 日)。“牛顿的第零定律：从倾听学生中学习”。物理教师，43 (1): 41–45。Bibcode:2005PhTea..43...41S。doi:10.1119/1.1845990。ISSN 0031-921X。
Greiner, Walter (2003)。《经典力学：点粒子与相对论》。纽约：Springer。p. 135。ISBN 978-0-387-21851-9。
Wachter, Armin；Hoeber, Henning (2006)。《理论物理学纲要》。纽约：Springer。p. 6。ISBN 978-0-387-25799-0。
Tait, Peter Guthrie (1889)。“力学”。《大英百科全书》第 15 卷（第 9 版）。第 715–716 页。
Heaviside, Oliver (1905 年 8 月)。“电子的横向动量”。自然，72 (1870): 429。Bibcode:1905Natur..72Q.429H。doi:10.1038/072429a0。ISSN 0028-0836。S2CID 4016382。
Nicodemi, Olympia (2010 年 2 月 1 日)。“伽利略与奥雷姆：谁是现代的？谁是中世纪的？”。数学杂志，83 (1): 24–32。doi:10.4169/002557010X479965。ISSN 0025-570X。S2CID 122113958。
Scholberg, Kate (2020)。“常见问题：抛体运动”。物理 361。2022 年 1 月 16 日获取。
Carli, Marta；Lippiello, Stefania；Pantano, Ornella；Perona, Mario；Tormen, Giuseppe (2020 年 3 月 19 日)。“测试学生在纯数学环境和物理环境中使用导数、积分和向量的能力”。物理评论物理教育研究，16 (1): 010111。Bibcode:2020PRPER..16a0111C。doi:10.1103/PhysRevPhysEducRes.16.010111。hdl:11577/3340932。ISSN 2469-9896。S2CID 215832738。
Boas, Mary L. (2006)。《物理科学中的数学方法》（第 3 版）。霍博肯，新泽西：Wiley。ISBN 978-0-471-19826-0。OCLC 61332593。
Brown, Mike (2010)。《我如何杀死冥王星，以及它为何咎由自取》（第 1 版）。纽约：Spiegel & Grau。ISBN 978-0-385-53108-5。OCLC 495271396。
Topper, D.; Vincent, D. E. (1999 年 1 月 1 日)。“牛顿抛射体图的分析”。欧洲物理学杂志，20 (1): 59–66。Bibcode:1999EJPh...20...59T。doi:10.1088/0143-0807/20/1/018。ISSN 0143-0807。S2CID 250883796。
Hand, Louis N.; Finch, Janet D. (1998)。《解析力学》。剑桥：剑桥大学出版社。ISBN 0-521-57327-0。OCLC 37903527。
Billah, K. Yusuf; Scanlan, Robert H. (1991 年 2 月 1 日)。“共振、塔科马海峡大桥坍塌与本科物理教材” (PDF)。美国物理学杂志，59 (2): 118–124。Bibcode:1991AmJPh..59..118B。doi:10.1119/1.16590。ISSN 0002-9505。
Chabay, Ruth; Sherwood, Bruce; Titus, Aaron (2019 年 7 月)。“一种统一的、现代的方法教授基础物理中的能量”。美国物理学杂志，87 (7): 504–509。Bibcode:2019AmJPh..87..504C。doi:10.1119/1.5109519。ISSN 0002-9505。S2CID 197512796。
Hughes-Hallett, Deborah；McCallum, William G.；Gleason, Andrew M.；等 (2013)。《微积分：单变量与多变量》（第 6 版）。霍博肯，新泽西：Wiley。ISBN 978-0-470-88861-2。OCLC 794034942。
Lyublinskaya, Irina E. (1998 年 1 月)。“中心碰撞——一般情况”。物理教师，36 (1): 18–19。Bibcode:1998PhTea..36...18L。doi:10.1119/1.879949。ISSN 0031-921X。
Close, Hunter G.; Heron, Paula R. L. (2011 年 10 月)。“学生对经典粒子角动量的理解”。美国物理学杂志，79 (10): 1068–1078。Bibcode:2011AmJPh..79.1068C。doi:10.1119/1.3579141。ISSN 0002-9505。
Mungan, Carl E. (2005 年 3 月 1 日)。“关于‘离心率作为一个向量’的另一个评论”。欧洲物理学杂志，26 (2): L7–L9。doi:10.1088/0143-0807/26/2/L01。ISSN 0143-0807。S2CID 121740340。
Saggio, Maria Luisa (2013 年 1 月 1 日)。“博林变换：连接胡克与牛顿的隐藏对称性”。欧洲物理学杂志，34 (1): 129–137。Bibcode:2013EJPh...34..129S。doi:10.1088/0143-0807/34/1/129。ISSN 0143-0807。S2CID 119949261。
Barrow-Green, June (1997)。《庞加莱与三体问题》。美国数学学会。第 8–12 页。Bibcode:1997ptbp.book.....B。ISBN 978-0-8218-0367-7。
Barrow-Green, June (2008)。“三体问题”。见 Gowers, Timothy；Barrow-Green, June；Leader, Imre（编）。《普林斯顿数学指南》。普林斯顿大学出版社。第 726–728 页。ISBN 978-0-691-11880-2。OCLC 682200048。
Breen, Barbara J.; Weidert, Christine E.; Lindner, John F.; Walker, Lisa May；Kelly, Kasey；Heidtmann, Evan (2008 年 4 月)。“令人尴尬的并行计算的邀请”。美国物理学杂志，76 (4): 347–352。Bibcode:2008AmJPh..76..347B。doi:10.1119/1.2834738。ISSN 0002-9505。
McCandlish, David (1973 年 7 月)。Shirer, Donald L.（编）。“用计算机求解三体问题”*。美国物理学杂志，41 (7): 928–929。doi:10.1119/1.1987423。ISSN 0002-9505。
Masoliver, Jaume; Ros, Ana (2011 年 3 月 1 日)。“可积性与混沌：经典的不确定性”。欧洲物理学杂志，32 (2): 431–458。arXiv:1012.4384。Bibcode:2011EJPh...32..431M。doi:10.1088/0143-0807/32/2/016。ISSN 0143-0807。S2CID 58892714。
Laws, Priscilla W. (2004 年 4 月)。“关于振荡、决定论和混沌的单元，适用于初级物理学生”。美国物理学杂志，72 (4): 446–452。Bibcode:2004AmJPh..72..446L。doi:10.1119/1.1649964。ISSN 0002-9505。
Zee, Anthony (2020)。《夜航物理》。普林斯顿大学出版社。第 363–364 页。ISBN 978-0-691-18254-4。OCLC 1288147292。
Han-Kwan, Daniel; Iacobelli, Mikaela (2021 年 4 月 7 日)。“从牛顿第二定律到欧拉完美流体方程”。美国数学学会会刊，149 (7): 3045–3061。arXiv:2006.14924。doi:10.1090/proc/15349。ISSN 0002-9939。S2CID 220127889。
Saari, Donald G.; Xia, Zhihong (1995 年 5 月)。“有限时间内通向无穷大” (PDF)。美国数学学会通报，42: 538–546。
Baez, John C. (2021)。“与连续统的斗争”。见 Anel, Mathieu；Catren, Gabriel（编）。《物理学中的新空间：形式与概念的反思》。剑桥大学出版社。第 281–326 页。arXiv:1609.01421。ISBN 978-1-108-49062-7。OCLC 1195899886。
Fefferman, Charles L. (2006)。“Navier–Stokes 方程的存在性与光滑性”。见 Carlson, James；Jaffe, Arthur；Wiles, Andrew（编）。《千年大奖问题》 (PDF)。普罗维登斯，罗德岛：美国数学学会与克莱数学研究所。第 57–67 页。ISBN 978-0-821-83679-8。OCLC 466500872。
Ehrenfest, Paul；Ehrenfest, Tatiana (1990) [1959]。《统计力学方法的概念基础》。纽约：Dover 出版社。p. 18。ISBN 0-486-66250-0。OCLC 20934820。
Kardar, Mehran (2007)。《粒子的统计物理学》。剑桥大学出版社。ISBN 978-0-521-87342-0。OCLC 860391091。
Byers, Nina (2006)。“埃米·诺特”。见 Byers, Nina；Williams, Gary（编）。《走出阴影：20 世纪女性对物理学的贡献》。剑桥：剑桥大学出版社。第 83–96 页。ISBN 978-0-521-82197-1。OCLC 1150964892。
LeGresley, Sarah E.; Delgado, Jennifer A.; Bruner, Christopher R.; Murray, Michael J.; Fischer, Christopher J. (2019 年 9 月 13 日)。“为初级物理设计的微积分增强能量优先课程提高了学生在本地和后续课程中的表现”。物理评论物理教育研究，15 (2): 020126。Bibcode:2019PRPER..15b0126L。doi:10.1103/PhysRevPhysEducRes.15.020126。hdl:1808/29610。ISSN 2469-9896。S2CID 203484310。
Ball, Philip (2019 年 9 月 13 日)。“在力学之前教授能量”。物理学，12: 100。Bibcode:2019PhyOJ..12..100B。doi:10.1103/Physics.12.100。S2CID 204188746。
Houchmandzadeh, Bahram (2020 年 5 月)。“哈密顿–雅可比方程：一种替代方法”。美国物理学杂志，88 (5): 353–359。arXiv:1910.09414。Bibcode:2020AmJPh..88..353H。doi:10.1119/10.0000781。ISSN 0002-9505。S2CID 204800598。
Rosen, Nathan (1965 年 2 月)。“经典力学中的混合态”。美国物理学杂志，33 (2): 146–150。Bibcode:1965AmJPh..33..146R。doi:10.1119/1.1971282。ISSN 0002-9505。
Weiner, J. H. (1974 年 11 月)。“哈密顿–雅可比方程的流体动力学类比”。美国物理学杂志，42 (11): 1026–1028。Bibcode:1974AmJPh..42.1026W。doi:10.1119/1.1987920。ISSN 0002-9505。
Reichl, Linda E. (2016)。《统计物理学的现代课程》（第 4 版）。德国魏因海姆：Wiley-VCH。ISBN 978-3-527-69048-0。OCLC 966177746。
Mermin, N. David (1961 年 8 月)。“布朗运动的两种模型”。美国物理学杂志，29 (8): 510–517。Bibcode:1961AmJPh..29..510M。doi:10.1119/1.1937823。ISSN 0002-9505。
Kneubil, Fabiana B. (2016 年 11 月 1 日)。“打破牛顿第三定律：电磁实例”。欧洲物理学杂志，37 (6): 065201。Bibcode:2016EJPh...37f5201K。doi:10.1088/0143-0807/37/6/065201。ISSN 0143-0807。S2CID 126380404。
Tonnelat, Marie-Antoinette (1966)。《电磁理论与相对论原理》。多德雷赫特：D. Reidel。ISBN 90-277-0107-5。OCLC 844001。
Chu, Caroline S.; Lebrilla, Carlito B. (2010)。“质谱技术的现代方法导论”。见 Jue, Thomas（编）。《生物物理学的生物医学应用》。新泽西州托托瓦：Humana 出版社。第 137–154 页。doi:10.1007/978-1-60327-233-9_6。ISBN 978-1-60327-233-9。2022 年 3 月 24 日获取。
Panofsky, Wolfgang K. H.; Phillips, Melba (2005) [1962]。《经典电学与磁学》（第 2 版）。纽约州迈内奥拉：Dover 出版社。ISBN 0-486-43924-0。OCLC 56526974。
Bonga, Béatrice; Poisson, Eric; Yang, Huan (2018 年 11 月)。“旋转带电球体的自扭矩与角动量平衡”。美国物理学杂志，86 (11): 839–848。arXiv:1805.01372。Bibcode:2018AmJPh..86..839B。doi:10.1119/1.5054590。ISSN 0002-9505。S2CID 53625857。
Goldstein, Herbert; Poole, Charles P.; Safko, John L. (2002)。《经典力学》（第 3 版）。旧金山：Addison Wesley。ISBN 0-201-31611-0。OCLC 47056311。
Werner, Reinhard F. (2014 年 10 月 9 日)。“关于‘贝尔的贡献’的评论”。《物理学 A 杂志：数学与理论》, 47 (42): 424011。Bibcode:2014JPhA...47P4011W。doi:10.1088/1751-8113/47/42/424011。ISSN 1751-8113。S2CID 122180759。
Choquet-Bruhat, Yvonne (2009)。《广义相对论与爱因斯坦方程》。牛津：牛津大学出版社。ISBN 978-0-19-155226-7。OCLC 317496332。
Ellis, George F. R.; Williams, Ruth M. (2000)。《平直与曲率时空》（第 2 版）。牛津：牛津大学出版社。ISBN 0-19-850657-0。OCLC 44694623。
French, A. P. (1968)。《狭义相对论》。W. W. Norton and Company。p. 224。ISBN 0-393-09804-4。
Havas, Peter (1964 年 10 月 1 日)。“牛顿力学的四维表述及其与狭义和广义相对论的关系”。现代物理评论，36 (4): 938–965。Bibcode:1964RvMP...36..938H。doi:10.1103/RevModPhys.36.938。ISSN 0034-6861。...牛顿力学的通常假设是，力由粒子的同时位置（以及可能的其导数）决定，并且它们由牛顿第三定律联系起来。而在狭义相对论中，不可能做出这样的假设，因为同时性在该理论中不是不变的概念。
Stavrov, Iva (2020)。《时空曲率及几何分析导论》。罗德岛州普罗维登斯：美国数学学会。ISBN 978-1-4704-6313-7。OCLC 1202475208。
Wheeler, John Archibald (2010 年 6 月 18 日)。《几何子、黑洞与量子泡沫：物理学人生》。W. W. Norton & Company。ISBN 978-0-393-07948-7。
Kersting, Magdalena (2019 年 5 月)。“曲率时空中的自由落体——如何在广义相对论中可视化引力”。物理教育，54 (3): 035008。Bibcode:2019PhyEd..54c5008K。doi:10.1088/1361-6552/ab08f5。hdl:10852/74677。ISSN 0031-9120。S2CID 127471222。
Prescod-Weinstein, Chanda (2021)。《混乱的宇宙：暗物质、时空与被延迟的梦想之旅》。纽约，NY：Bold Type Books。ISBN 978-1-5417-2470-9。OCLC 1164503847。
Goodstein, Judith R. (2018)。《爱因斯坦的意大利数学家：Ricci, Levi-Civita 与广义相对论的诞生》。罗德岛州普罗维登斯：美国数学学会。p. 143。ISBN 978-1-4704-2846-4。OCLC 1020305599。
Mermin, N. David (1993)。“隐藏变量与约翰·贝尔的两个定理”。现代物理评论，65 (3): 803–815。arXiv:1802.10119。Bibcode:1993RvMP...65..803M。doi:10.1103/RevModPhys.65.803。S2CID 119546199。它是量子力学的一个基本教义，即测量通常不会揭示被测量属性的预先存在的值。
Schaffer, Kathryn；Barreto Lemos, Gabriela (2019 年 5 月 24 日)。“消除物体性：量子物理学的‘是什么’与‘那么怎样’导论”。科学基础，26: 7–26。arXiv:1908.07936。doi:10.1007/s10699-019-09608-5。ISSN 1233-1821。S2CID 182656563。
Marshman, Emily；Singh, Chandralekha (2017 年 3 月 1 日)。“研究和改进学生对量子力学中测量物理可观测量的概率分布的理解”。欧洲物理学杂志，38 (2): 025705。Bibcode:2017EJPh...38b5705M。doi:10.1088/1361-6404/aa57d1。ISSN 0143-0807。S2CID 126311599。
Cohen-Tannoudji, Claude; Diu, Bernard; Laloë, Franck (2005)。《量子力学》。Susan Reid Hemley、Nicole Ostrowsky、Dan Ostrowsky 译。John Wiley & Sons。ISBN 0-471-16433-X。
Peres, Asher (1993)。《量子理论：概念与方法》。Kluwer。ISBN 0-7923-2549-4。OCLC 28854083。
D. Bilodeau，引自 Fuchs, Christopher A. (2011 年 1 月 6 日)。《伴随量子信息成长》。剑桥大学出版社。第 310–311 页。ISBN 978-0-521-19926-1。OCLC 759812415。
Caspar, Max (2012) [1959]。《开普勒》。C. Doris Hellman 译。Dover。p. 178。ISBN 978-0-486-15175-5。OCLC 874097920。
Ugaglia, Monica (2015)。“亚里士多德的流体静力学物理”。《比萨高等师范学校文学院年刊》, 7 (1): 169–199。ISSN 0392-095X。JSTOR 43915795。
Straulino, S.; Gambi, C. M. C.; Righini, A. (2011 年 1 月)。“根据伽利略的实验研究浮力与表面张力”。美国物理学杂志，79 (1): 32–36。Bibcode:2011AmJPh..79...32S。doi:10.1119/1.3492721。hdl:2158/530056。ISSN 0002-9505。亚里士多德在其《物理学》中主张，固态水应该比相同体积的液态水更重。我们知道这一说法不正确，因为冰的密度低于水（氢键在固态相中形成开放的晶体结构），因此冰能够浮起。[…] 亚里士多德的浮力理论认为，流体中的物体受到流体抗拒被穿透的抵抗力支撑，就像一块大木头可以支撑击打它的斧头，或者蜂蜜可以支撑一把勺子。根据这一理论，一艘船在浅水中比在深海中下沉得更多，就像一把斧头可以轻易穿透甚至劈开一块小木头，而无法穿透一块大木头一样。
Sorabji, Richard (2010)。《约翰·斐洛波诺斯》。见*《斐洛波诺斯与对亚里士多德科学的拒斥》（第 2 版）。伦敦大学古典研究所。ISBN 978-1-905-67018-5。JSTOR 44216227。OCLC 878730683。
Maier, Anneliese (1982)。Sargent, Steven D.（编）。《精确科学的门槛》。宾夕法尼亚大学出版社。ISBN 978-0-812-27831-6。OCLC 495305340。
另见： (1).Eaton, Philip; Vavruska, Kinsey; Willoughby, Shannon (2019 年 4 月 25 日)。“通过力概念测试探讨教学前后非牛顿世界观的变化”。物理评论物理教育研究，15 (1): 010123。Bibcode:2019PRPER..15a0123E。doi:10.1103/PhysRevPhysEducRes.15.010123。ISSN 2469-9896。S2CID 149482566。
(2).Robertson, Amy D.; Goodhew, Lisa M.; Scherr, Rachel E.; Heron, Paula R. L. (2021 年 3 月)。“与牛顿物理学相连续的冲力式推理”。物理教师，59 (3): 185–188。doi:10.1119/10.0003660。ISSN 0031-921X。S2CID 233803836。
(3)Robertson, Amy D.; Goodhew, Lisa M.; Scherr, Rachel E.; Heron, Paula R. L. (2021 年 3 月 30 日)。“大学生理解力的概念资源”*。物理评论物理教育研究，17 (1): 010121。Bibcode:2021PRPER..17a0121R。doi:10.1103/PhysRevPhysEducRes.17.010121。ISSN 2469-9896。S2CID 243143427。
Blackwell, Richard J. (1966)。“笛卡尔的运动定律”。Isis, 57 (2): 220–234。doi:10.1086/350115。JSTOR 227961。S2CID 144278075。
Galilei, G. (1954) [1638, 1914]。Crew, H.; De Salvio, A.（编）。《关于两种新科学的对话》。Dover 出版社。p. 268。
Galilei, G. (1974) [1638]。《两种新科学，包含重心与碰撞力的研究》。S. Drake 译。威斯康星大学出版社。pp. 217 [268]。
Hellman, C. Doris (1955)。“文艺复兴时期的科学：一项概述”。文艺复兴新闻, 8 (4): 186–200。doi:10.2307/2858681。ISSN 0277-903X。JSTOR 2858681。
LoLordo, Antonia (2007)。《皮埃尔·伽森狄与早期现代哲学的诞生》。纽约：剑桥大学出版社。pp. 175–180。ISBN 978-0-511-34982-9。OCLC 182818133。
Descartes, R. (2008) [1644]。Bennett, J.（编）。《哲学原理》 (PDF)。Part II, § 37, 39。
Blackwell, Richard J.; Huygens, Christiaan (1977)。“克里斯蒂安·惠更斯的碰撞体运动”。Isis, 68 (4): 574–597。doi:10.1086/351876。JSTOR 230011。S2CID 144406041。
Pourciau, Bruce (2011 年 10 月)。“牛顿第二定律真的来自牛顿吗？”。美国物理学杂志, 79 (10): 1015–1022。Bibcode:2011AmJPh..79.1015P。doi:10.1119/1.3607433。ISSN 0002-9505。
Fara, Patricia (2003 年 8 月 15 日)。“牛顿真的是牛顿主义者吗？”。科学, 301 (5635): 920。doi:10.1126/science.1088786。ISSN 0036-8075。S2CID 170120455。
Higgitt, Rebekah (2015)。《19 世纪的科学与文化：重现牛顿》。纽约：Taylor & Francis。p. 147。ISBN 978-1-317-31495-0。OCLC 934741893。
Dobbs, Betty Jo Teeter (1975)。《牛顿炼金术的基础：或 “绿色狮子的狩猎”》。剑桥大学出版社。pp. 211–212。ISBN 9780521273817。OCLC 1058581988。
West, Richard (1980)。《永不停歇》。剑桥大学出版社。p. 390。ISBN 9780521231435。OCLC 5677169。
Newman, William R. (2016)。“对牛顿炼金术的初步重新评估”。见《剑桥牛顿指南》 (第 2 版)。剑桥大学出版社。pp. 454–484。ISBN 978-1-107-01546-3。OCLC 953450997。
Nummedal, Tara (2020 年 6 月 1 日)。“William R. Newman. 牛顿炼金术士：科学、谜团与寻找自然的‘神秘之火’”。Isis, 111 (2): 395–396。doi:10.1086/709344。ISSN 0021-1753。S2CID 243203703。
Aldersey-Williams, Hugh (2020)。《荷兰之光：克里斯蒂安·惠更斯与欧洲科学的形成》。伦敦：Picador。ISBN 978-1-5098-9333-1。OCLC 1144105192。
Cohen, I. Bernard (1962)。“牛顿《我不虚设假说》的首个英文版本”。Isis, 53 (3): 379–388。doi:10.1086/349598。ISSN 0021-1753。JSTOR 227788。S2CID 144575106。
Jammer, Max (1999) [1962]。《力的概念：动力学基础研究》。纽约州 Mineola：Dover Publications。pp. 91, 127。ISBN 978-0-486-40689-3。OCLC 40964671。
Slowik, Edward (2021 年 10 月 15 日)。“笛卡尔的物理学”。斯坦福哲学百科全书。检索日期：2022 年 3 月 6 日。
Erlichson, Herman (1997 年 2 月)。“年轻的惠更斯解决了弹性碰撞的问题”。美国物理学杂志, 65 (2): 149–154。Bibcode:1997AmJPh..65..149E。doi:10.1119/1.18659。ISSN 0002-9505。
Smith, George E. (2006 年 10 月)。“活力争端：动力学黎明时期的争论”。今日物理, 59 (10): 31–36。Bibcode:2006PhT....59j..31S。doi:10.1063/1.2387086。ISSN 0031-9228。
Davies, E. B. (2009)。“对牛顿《自然哲学的数学原理》的一些反思”。英国科学史杂志, 42 (2): 211–224。doi:10.1017/S000708740800188X。ISSN 0007-0874。JSTOR 25592244。S2CID 145120248。
Smith, George E. (2020 年 12 月)。“牛顿的运动定律”。见 Schliesser, Eric; Smeenk, Chris（编）。《牛顿牛津手册》。牛津大学出版社。在线出版，doi:10.1093/oxfordhb/9780199930418.013.35。ISBN 978-0-199-93041-8。OCLC 972369868。
Patterson, Elizabeth C. (1969 年 12 月)。“玛丽·萨默维尔”。英国科学史杂志, 4 (4): 311–339。doi:10.1017/S0007087400010232。ISSN 0007-0874。S2CID 246612625。书并不是拉普拉斯作品的简单翻译，而是努力解释他的方法 “……通过这个方法，这些结果是从一个物质运动的通用方程推导出来的”，并希望使读者的数学技能达到理解拉普拉斯数学和思想的水平——然后以英语简明扼要地介绍他的伟大作品。当必要时，书中为原文添加了图解，并包括了物理力学和天文学中各种问题的证明……在出版后的近百年间，这本书一直是英国学校高等数学和天文学的教材。
Baron, Margaret E. (1969)。《微积分的起源》（第一版）。牛津：Pergamon 出版社。ISBN 978-1-483-28092-9。OCLC 892067655。
Dunlop, Katherine (2012 年 5 月)。“测量的数学形式与牛顿《自然哲学的数学原理》第一命题的论证”。Synthese, 186 (1): 191–229。doi:10.1007/s11229-011-9983-8。ISSN 0039-7857。S2CID 11794836。
Smith, George (2007 年 12 月 20 日)。《牛顿的自然哲学的数学原理》。斯坦福哲学百科全书。检索日期：2022 年 3 月 6 日。
Marquina, J. E.; Marquina, M. L.; Marquina, V.; Hernández-Gómez, J. J. (2017 年 1 月 1 日)。“莱昂哈德·欧拉与刚体力学”。欧洲物理学杂志, 38 (1): 015001。Bibcode:2017EJPh...38a5001M。doi:10.1088/0143-0807/38/1/015001。ISSN 0143-0807。S2CID 125948408。
Hesse, Mary B. (2005) [1961]。《力与场：物理学史上的远距离作用概念》（Dover 再版）。纽约州 Mineola：Dover 出版社。p. 189。ISBN 978-0-486-44240-2。OCLC 57579169。
Smith, George (2007 年 12 月 19 日)。《艾萨克·牛顿》。斯坦福哲学百科全书。检索日期：2022 年 3 月 6 日。这些关于行星运动理解的进步促使拉普拉斯在 1799 年至 1805 年间出版了《天体力学》四卷本，这部作品汇集了基于牛顿《自然哲学的数学原理》的所有理论和实证成果。从那时起，牛顿科学更多是基于拉普拉斯的研究，而非牛顿的。
Reichenberger, Andrea (2018 年 6 月)。“在 18 世纪力学的背景下，艾米丽·杜·夏特莱对运动定律的解释”。科学史与哲学研究 A, 69: 1–11。Bibcode:2018SHPSA..69....1R。doi:10.1016/j.shpsa.2018.01.006。PMID 29857796。S2CID 46923474。
Frontali, Clara (2014 年 9 月)。“物理术语的历史：‘能量’”。物理教育, 49 (5): 564–573。Bibcode:2014PhyEd..49..564F。doi:10.1088/0031-9120/49/5/564。ISSN 0031-9120。S2CID 122097990。
Gbur, Greg (2018 年 12 月 10 日)。“能量守恒的历史：爆炸、血液和啤酒（第一部分）”。骷髅与星辰。检索日期：2022 年 3 月 7 日。“能量守恒的历史：爆炸、血液和啤酒（第二部分）”。2018 年 12 月 29 日。检索日期：2022 年 3 月 7 日。“能量守恒的历史：爆炸、血液和啤酒（第三部分）”。2019 年 8 月 25 日。检索日期：2022 年 3 月 7 日。
Silva, Cibelle Celestino; de Andrade Martins, Roberto (2002 年 9 月)。“极性与轴向矢量与四元数”。美国物理学杂志, 70 (9): 958–963。Bibcode:2002AmJPh..70..958S。doi:10.1119/1.1475326。ISSN 0002-9505。
Reich, Karin (1996)。“矢量微积分在物理学中的出现：早期的几十年”。见 Schubring, Gert（编）。赫尔曼·君特·格拉斯曼（1809–1877）：有远见的数学家、科学家和新古典人文学者。波士顿科学哲学研究，第 187 卷。Kluwer 出版社。pp. 197–210。ISBN 978-9-048-14758-8。OCLC 799299609。