双精度和四精度浮点数笔记（C++）

贡献者： addis

本文处于草稿阶段。

double

根据 IEEE 754¹ 标准，双精度的格式是 1 bit 符号 + 11 bit 指数 + 52 bit 小数（mantissa）。
符号位也用于区分 0.（普通的 0. 就是 +0.）和 -0.，注意一定要有 “.”，整数零不区分正负），例如 1/0., 1/(-0.) 分别得到 inf, -inf，反之亦然。另外一些函数也对 -0. 敏感，例如 atan2。
0. == -0.，-2*0. 得 -0.，inf == inf，-inf == -inf，inf * 2 == inf，inf * 0 == nan。
无论哪种 nan 和自身都不相等，可以用这种方法来判断一个浮点数是否是 nan。也可以用 isnan()。

　　 C++ 浮点相关函数：

bool signbit(x) 获取符号位（对于 -0 来说，这不同于 (x < 0)）
ldexp(x, n) 计算 $x \times 2^n$；
double man = frexp(x, &exp2) 可以拆分 mantissa 和 exp。其中 0.5 <= man < 1；
int fpclassify(x) 可以用来给浮点数归类（返回 FP_NORMAL, FP_SUBNORMAL, FP_ZERO, FP_INFINITE, FP_NAN 之一）。
bool isfinite(x) 检查是否是 FP_NORMAL, FP_SUBNORMAL, FP_ZERO 之一。
bool isnormal(x) 检查 fpclassify 是否返回 FP_NORMAL。

ULP

　　 unit in the last place (ULP) 就是 mantissa 增加 1 bit 时表示的数增加多少。这等于 $2^{-52}\times 2^{e}$。$e$ 是双精度的指数（以 2 为底）。其中 $2^{-52}$ 一般记为 eps。

　　所以双精度的 mantissa 表示 1 时，相对精度就是 eps，表示 1-eps 时，相对精度就非常接近 eps/2（最小相对误差）。所以一般来说相对精度在二者之间。但一个例外就是当绝对值非常小时（小于 $2^{-1022}$）也就是 $2.225 \times 10^{-308} $），也就是 subnormal，mantissa 的第一 bit 可能并不是默认的 1，此时相对误差可能会变得很大。

需要多少位十进制数

　　需要多少位十进制数可以通过四舍五入精确表示任意的双精度数呢？$N$ 位有效数字的十进制数的相对误差介于 $10^{-N}$（前几位是 999... 时）和 $10^{-N+1}$（前几位是 1000... 时）之间。所以为了满足 eps/2（$1.11 \times 10^{-16} $）的相对误差，最多需要 17 位有效数字。

　　那么一个 double 能不能精确地用十进制表示呢？可以的，因为 eps 可以，但可能需要非常多的位数尤其是 2 的指数非常大或者非常小的时候可能会需要几百位，没有太大必要。

long double

　　在 x86 机器上，long double 一般是 1 bit 符号 + 15 bit 指数 + 64 bit 小数 = 80 bit，十进制大约是 18-19 位有效数字²。虽然 sizeof 是 16 字节，但实际上只使用了 10 字节³。long double 的运算是硬件支持的，所以比较快。

sizeof(Doub) = 8
sizeof(Ldoub) = 16

std::numeric_limits<Doub>::max() = 1.797693135e+308
std::numeric_limits<Ldoub>::max() = 1.189731495e+4932

std::numeric_limits<Doub>::min() = 2.225073859e-308
std::numeric_limits<Ldoub>::min() = 3.362103143e-4932

std::numeric_limits<Doub>::denorm_min() = 4.940656458e-324
std::numeric_limits<Ldoub>::denorm_min() = 3.645199532e-4951

std::numeric_limits<Doub>::epsilon() = 2.220446049e-16
std::numeric_limits<Ldoub>::epsilon() = 1.084202172e-19 // 2^(-63)

std::numeric_limits<Doub>::digits10 = 15
std::numeric_limits<Ldoub>::digits10 = 18

　　然而 sqrt 函数似乎并不会提高精度（仍然是 16 位）：

sqrt(2.)       = 1.4142135623730951454
sqrt(Ldoub(2)) = 1.4142135623730951454
precise val    = 1.4142135623730950488...

　　另外测试一下双精度的二进制表示（图 3 ），例如双精度的 10 表示为

01000000 00100100 (后面省略 48 个 0)

第一位 0 说明是正数，1 是负数。接下来 11 bit 先看成 unsigned，然后再减 $2^{10}-1 = 1023$，这里指数 10000000010 表示 $1026-1023 = 3$，于是指数项为 $2^{3} = 8$。所以要表示 10，小数项应该是 $10/8 = 1+1/4$。第 13 bit 表示 1/2，14 bit 表示 1/4，所以第 14 bit 是 1，后面的小数全是零。另外，由于 intel 的 x86 和 x86-64 都使用 little endian，所以在内存中实际上 byte 的顺序是相反的。

　　理论上指数部分可以表示 $-1023$ 到 $1024$ 之间的数，但首尾两个数有特殊用途，所以只能表示 $-1022$ 到 $1023$。当指数为 $-1023$ 时，仍然相当于指数为 $-1022$ 但小数部分前面不加 1（如果小数也都是零，那就表示 0，所以 0 除了第一 bit 其他都必须是 0）。当指数为 $1024$ 时，表示 inf（要求小数部分都是零，正负号仍然有效）或者 nan（0b1... 表示安静的 qNaN，0b0..1.. 表示会发错误信号的 sNaN）。

　　双精度类型可以表示 -2e53 到 2e53 的每一个整数，更小或更大的整数有的也可以表示（事实上此时只可以表示整数），只是不连续。

std::numeric_limits<double>::max() = 1.797693135e+308
01111111 11101111 11111111 11111111 11111111 11111111 11111111 11111111
std::numeric_limits<double>::min() = 2.225073859e-308 = 2^-1022
00000000 00010000 00000000 00000000 00000000 00000000 00000000 00000000
std::numeric_limits<double>::epsilon() = 2.22e-16 = 2^-52
00111100 10110000 00000000 00000000 00000000 00000000 00000000 00000000
std::numeric_limits<double>::denorm_min() = 4.940656458e-324 = 2^-1074
00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000001
std::numeric_limits<double>::denorm_min()*11
00000000 00000000 00000000 00000000 00000000 00000000 00000000 00001011
double 1/0.:
01111111 11110000 00000000 00000000 00000000 00000000 00000000 00000000
double max()*2 (正无穷， 同 1/0.):
01111111 11110000 00000000 00000000 00000000 00000000 00000000 00000000
double -max()*2 (负无穷):
11111111 11110000 00000000 00000000 00000000 00000000 00000000 00000000
double sqrt(-1.) (NaN):
11111111 11111000 00000000 00000000 00000000 00000000 00000000 00000000

其中 denorm_min() 比较特殊，当指数 bit 全为 0 的时候，指数为 -1022 而不是 -1023，且小数部分前面不加 1。这叫做 denominize。

1. 四精度

　　⁴使用四精度比使用任意精度类型（如 MPFR 或 Flint 库）要快得多，因为任意精度浮点数是动态分配内存的。

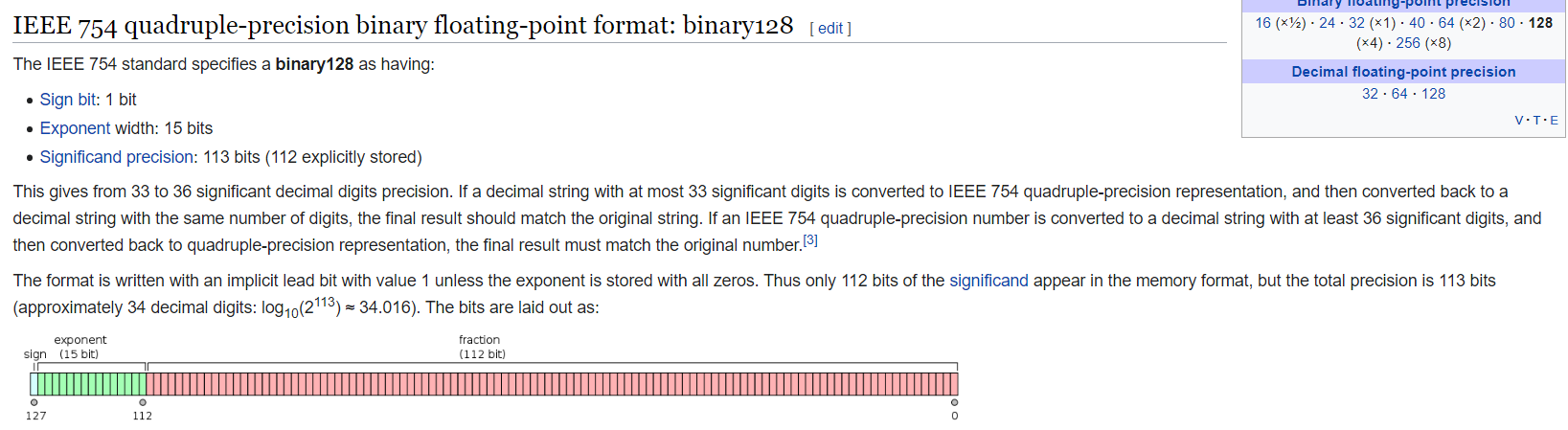
　　如果想完全利用 16 字节，见 GCC/g++ 编译器的 __float128 类型（文档）。相当于 FORTRAN 的 QUAD real。有 112 bit 小数，15 bit 指数和 1 bit 正负号（图 1 ）。实测的 bit 表示和上面二进制的同理（也存在两个奇怪的地方）。

图 1：见 Wikipedia

　　加上头文件 #include <quadmath.h>，使用 g++ 编译，编译时加上选项 -lquadmath 和 -fext-numeric-literals 即可。

　　 __complex128 是对应的四精度复数类型，相当于两个 __float128。

FLT128_MAX = 1.1897e+4932
FLT128_MIN = 3.3621e-4932
FLT128_EPSILON = 1.9259e-34 // 2e-112
FLT128_DENORM_MIN = 6.4752e-4966
FLT128_MANT_DIG = 113 // 包括正负位
FLT128_MAX_EXP = 16384 // 2e14
FLT128_DIG = 33 // 33-34 位十进制有效数字
M_PIq = 3.141592653589793238462643383279503 // 精确到最后一位
sqrtq(3) = 1.732050807568877293527446341505872 // 精确到最后一位

　　给 __complex128 的实部和虚部分别赋值：

__complex128 y;
__real__ y = 实部;
__imag__ y = 虚部;

看来还是用 std::complex<__real128> 比较好。

　　另见 “C++ 高精度计算资源列表”。

1. ^ 参考 Wikipedia 相关页面。
2. ^ Visual Studio 中据说 long double 和 double 是一样的。
3. ^ 详见这里的 x86 extended precision format 一节
4. ^ 参考 Wikipedia 相关页面。